本記事の内容
本記事は、レオンチェフ方程式の1次元と2次元場合について解説する記事です。
本記事を読むにあたり、レオンチェフ方程式について知っている必要があるため、以下の記事も合わせてご覧ください。
レオンチェフ方程式の軽い復習
レオンチェフ方程式について軽く復習します。
産業連関表
以下の表を産業連関表といいます。
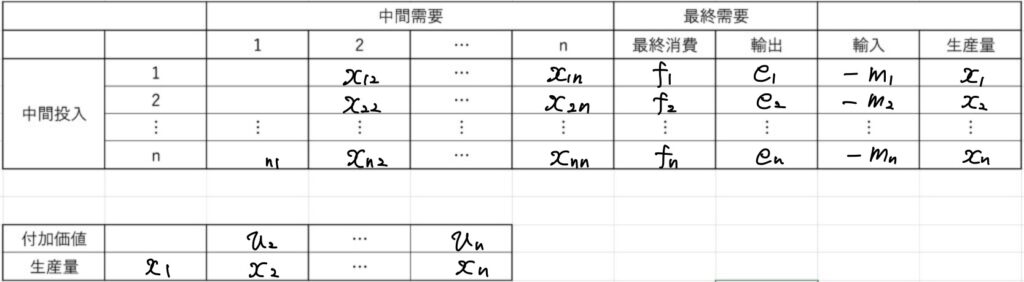
レオンチェフ方程式
ある年度の産業連関表が上記のように与えられたとします。
投入係数を\(a_{ij}\)、すなわち部門\(i\)からの生産量の内、部門\(j\)に需要されて使われる量は\(x_{ij}=a_{ij}x_j\)とします。
ただし、\(a_{ij}=0\)の場合は、\(i\)から\(j\)には供給が無い、と考えます。
部門\(i\)にシステムの外部から需要される量は\(b_i=f_i+e_i-m_i\)です。
従って、需要量に見合った生産が行われたのであれば、一般の場合も次の等式を得ることが出来ます。
\begin{eqnarray}
x_1&=&a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n+b_1\\
x_2&=&a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n+b_2\\ \tag{\(\ast\)}
\vdots&&\quad\vdots\qquad \quad\vdots\qquad\quad\qquad\quad \vdots\quad \quad\vdots\\
x_n&=&a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n+b_n\\
\end{eqnarray}
ここで、右辺が需要量、左辺が生産量を表しています。
この等式を、\(a_{ij}\geq0\)が予め与えられたとき(これも投入係数呼ぶことにしますが、不等式(2)は仮定しません)、最終需要料(厳密には輸入量を引いたもの)\(b_1,\dots,b_n\ (b_i\geq0)\)に対して、それに見合う生産量(均衡産出高)\(x_1,\dots,x_n\ (x_i\geq0)\)を求める連立方程式と見ます。
要するに、\(a_{ij}\geq0\)が与えられたときに、\(b_1,\dots,b_n\ (b_i\geq0)\)に対して\(x_1,\dots,x_n\ (x_i\geq0)\)を求める連立方程式と見る、ということです。
この方程式\((\ast)\)をレオンチェフ方程式あるいは均衡産出高モデルと言ったのでした。
もし、正の付加価値が付けられるならば、更に不等式
$$
a_{1j}+a_{2j}+\cdots+a_{nj}<1\tag{\(\ast\ast\)}
$$
が成り立ちます。
viable
viable(実行可能)
均衡産出高もである、あるいは投入係数に当たる\(\left\{a_{ij}\right\}\)がviable(実行可能)とは、レオンチェフ方程式が任意の\(b_1,\dots,b_n\ (b_i\geq0)\)に対して一意的な解\(x_1,\dots,x_n\ (x_i\geq0)\)を持つことをいう。証明したいこと
証明したいことは以下です。
定理0.
- ある\(b_1>0,\dots,b_n>0\)に対してレオンチェフ方程式\((\ast)\)が解\(x_1\geq0,\dots,x_n\geq0\)を持つならば、\(\left\{a_{ij}\right\}\)はviableである。
- 条件\((\ast\ast)\)の下で、\(\left\{a_{ij}\right\}\)はviableである。
これは特に、最終需要料(-輸入量)が正、または付加価値が正であるような産業連関表から得られる投入係数はviableだ、ということを意味しています。
勿論、「成り立ちそうだな」という定理です(主観ですが)。
詳しくは、【幾何学の基礎シリーズ】グラフ理論編 その13を御覧ください。
今回のお話
目標は定理0.の証明なのですが、まずは手始めに\(n=1,2\)の場合、すなわち、部門の数が1個の場合と2個の場合について考えるのが今回です。
少し踏み込んだ話をすれば、部門の数が一般の場合の均衡産出高を求める問題を扱うには、行列と行列式の理論が必要となります。
一般の理論に進む前に、今回はワンクッションとして\(n=1,2\)の場合について扱おう、という話です。
\(n=1\)のときの定理0.の証明
\(n=1,2\)の場合を証明する前に、そもそも\(n=1,2\)のときに定理0.の\((\ast)\)が成り立つのか?ということを確認してみます。\(n=1\)の場合、すなわち1つの産業部門からなるシステムで、外部からの最終需要が\(b\)、投入係数を\(a>0\)とします。
この場合の均衡産出量\(x\)が満たす方程式は
$$
x=ax+b
$$
となります。
確かに、この式は\((\ast)\)の\(n=1\)の場合となっていることに注意です。
これが1つ固定された\(b\geq0\)に対して解\(x\geq0\)を持つためには、\(a<1\)でなければなりません。
勿論、\(a<1\)であれば、任意の\(b\geq0\)に対して解\(x\geq0\)を持ちます。
従って、\(n=1\)のときは定理0.は正しいです(\(a<1\)だから定理0.の(2)も正しいです)。
\(n=2\)の場合
\(n=2\)の場合、すなわち産業部門が2つの場合に定理0.が正しいかどうかを確かめてみましょう。
定理0.の(1)について
レオンチェフ方程式は
\begin{eqnarray}
&&a_{11}x_1+a_{12}x_2+b_1=x_1 \tag{1}\\
&&a_{21}x_1+a_{22}x_2+b_2=x_2 \tag{2}
\end{eqnarray}
です。
\(b_1,b_2\geq0\)として、解\(x_1,x_2\geq0\)が存在するとします。
\begin{eqnarray}
&&\left( 1-a_{11}\right)x_1=a_{12}x_2+b_1>0,\\
&&\left( 1-a_{22}\right)x_2=a_{21}x_1+b_2>0
\end{eqnarray}
であるから、\(a_{11}<1\)、\(a_{22}<1\)です。
さらに、\(x_1,x_2>0\)でなければなりません。
(1)を消去法により得時の方法で変形すれば、
\begin{eqnarray}
\left( 1-a_{11}-a_{22}+a_{11}a_{22}-a{12}a_{21}\right)x_1&=&\left(1-a_{22} \right)b_1+a_{12}b_2\\
\left( 1-a_{11}-a_{22}+a_{11}a_{22}-a{12}a_{21}\right)x_2&=&\left(1-a_{11} \right)b_2+a_{21}b_1\\
\end{eqnarray}
が得られます。
ここで、これらの右辺は、先程示したことから正です。
故に、\(x_1,x_2>0\)であるから
$$
1-a_{11}-a_{22}+a_{11}a_{22}-a{12}a_{21}>0
$$
です。
特に(1)は、一般の\(b_1,b_2\geq0\)に対しても一意的に解けて、しかもその解\(x_1,x_2\)は\(0\)以上だと分かります。
定理0.の(2)について
定理0.の(2)を証明する前に、viableであるための投入係数の条件を与えます。
命題1.
投入係数\(\left\{a_{ij}\right\}\)がviableであるための必要十分条件は \begin{eqnarray} 1-a_{11}>0,\\ 1-a_{11}-a_{22}+a_{11}a_{22}-a_{12}a_{21}>0 \end{eqnarray} である。命題1.の証明
viableであるとき\(\left\{a_{ij}\right\}\)に関する2つの不等式が成り立つことはすでに証明済みです。
逆に2つの不等式を仮定します。
2番目の式は
$$
\left( 1-a_{11}\right)\left(1-a_{22} \right)>a_{12}a_{21}\geq0
$$
と表現できます。
故に\(1-a_{22}>0\)が導けます。
解の公式
\begin{eqnarray}
x_1&=&\frac{\left( 1-a_{22}\right)b_1+a_{12}b_2}{1-a_{11}-a_{22}+a_{11}a_{22}-a{12}a_{21}}\\
x_2&=&\frac{\left( 1-a_{11}\right)b_2+a_{21}b_1}{1-a_{11}-a_{22}+a_{11}a_{22}-a{12}a_{21}}
\end{eqnarray}
を見れば、任意の\(b_1,b_2\geq0\)に対して一意的な非負解\(x_1,x_2\)を持つことが分かります。
命題1.の証明終わり
この命題1.は一般のレオンチェフ方程式に拡張されます。
別の形の条件を与えます。
二次方程式
$$
x^2-\left( a_{11}+a_{22}\right)x+\left( a_{11}a_{22}-a_{12}a_{21}\right)=0
$$
を考えます。
「どうしてこの方程式を考えるのか?」というこの方程式の”意味づけ”は後述します。
この二次方程式の判別式\(D\)は
\begin{eqnarray}
D&=&\left( a_{11}+a_{22}\right)^2-4\left( a_{11}a_{22}-a_{12}a_{21}\right)\\
&=&a_{11}^2+a_{22}^2+2a_{11}a_{22}-4\left( a_{11}a_{22}-a_{12}a_{21}\right)\\
&=&\left( a_{11}-a_{22}\right)^2+4a_{12}a_{21}\geq0
\end{eqnarray}
だから、解は実数です。
解は
$$
x=\frac{a_{11}+ a_{22}\pm\sqrt{D}}{2}
$$
です。
\begin{eqnarray}
\lambda_1&=&\frac{a_{11}+ a_{22}+\sqrt{D}}{2}\\
\lambda_2&=&\frac{a_{11}+ a_{22}-\sqrt{D}}{2}
\end{eqnarray}
とすると、\(\lambda_1\geq0\)であり、かつ
$$
\left|\lambda_2\right|\leq\lambda_1
$$
が成り立っています。
命題2.
方程式(1)において、任意の\(b_1.b_2\geq0\)に対して一意的な非負解\(x_1,x_2\)を持つための必要十分条件は、\(\lambda_1<1\)である。命題2.の証明
\(f(x)=x^2-\left( a_{11}+a_{22}\right)x+\left( a_{11}a_{22}-a_{12}a_{21}\right)\)とします。
このとき
\begin{eqnarray}
f(1)&=&1-a_{11}-a_{22}+\left( a_{11}a_{22}-a_{12}a_{21}\right),\\
f(-1)&=&1+a_{11}+a_{22}+\left( a_{11}a_{22}-a_{12}a_{21}\right)\\
&=&\left[1-a_{11}-a_{22}+\left( a_{11}a_{22}-a_{12}a_{21}\right) \right]+2\left( a_{11}+a_{22}\right)
\end{eqnarray}
です。
故に、もし仮に\(1-a_{11}-a_{22}+\left( a_{11}a_{22}-a_{12}a_{21}\right)>0\)であれば、\(f(1)\)、\(f(-1)\)の双方がともに正であり、二次関数\(f(x)\)のグラフを見れば、\(-1<\lambda_1,\lambda_2<1\)が成り立つことが分かります。
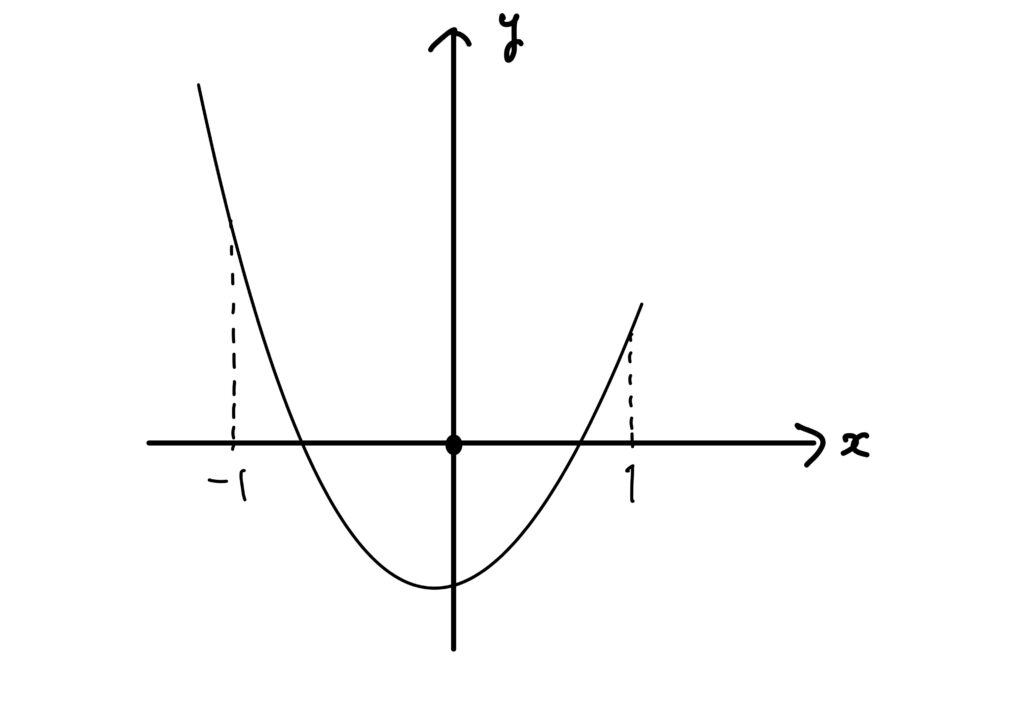
逆に、\(-1<\lambda_1,\lambda_2<1\)とすると、これもグラフから\(f(1)>0\)であるから
$$
f(1)=1-a_{11}-a_{22}+\left( a_{11}a_{22}-a_{12}a_{21}\right)>0
$$
です。
あとは、\(a_{11}<1\)であればOKです。
\(\displaystyle\lambda_1=\frac{a_{11}+ a_{22}+\sqrt{D}}{2}\)だから、\(\lambda_1<1\)という仮定から\(a_{11}+a_{22}<2\)です。
故に\(a_{11}<1\)かまたは\(a_{22}<1\)が成り立たなければなりません。
仮に\(a_{11}<1\)であれば、証明終了です。
そこで、\(a_{22}<1\)だとしましょう。
\(a_{11}\leq a_{22}\)の場合も証明終了です。
\(a_{11}< a_{22}\)とします。
$$
D=\left( a_{11}-a_{22}\right)^2+4a_{12}a_{21}\geq\left( a_{11}-a_{22}\right)^2
$$
だから、\(\lambda<1\)を再度使うことで
$$
a_{11}+a_{22}+\left|a_{11}-a_{22}\right|<2
$$
が得られます。
ここで、\(a_{22}<a_{11}\)と仮定しているから、左辺は
$$
a_{11}+a_{22}+\left|a_{11}-a_{22}\right|=2a_{11}
$$
であり、従って\(a_{11}<1\)となります。
命題2.の証明終わり
この命題も一般化されます。
命題3.
\(a_{11}+a_{21}\leq\lambda_1\leq a_{12}+a_{22}\)または\(a_{12}+a_{22}\leq\lambda_1\leq a_{11}+a_{21}\)が成り立つ。言い換えれば、 $$ \min\left\{a_{11}+a_{21},a_{12}+a_{22}\right\}\leq\lambda_1\leq \max\left\{a_{11}+a_{21},a_{12}+a_{22}\right\} $$ が成り立つ。命題3.の証明
\(a_{11}+a_{21}\leq a_{12}+a_{22}\)の場合を考えます。
二次関数\(f(x)\)が
\begin{eqnarray}
&&f\left( a_{12}+a_{22}\right)\geq0,\\
&&f\left( a_{11}+a_{21}\right)\leq0
\end{eqnarray}
を満たすことを示せば、\( a_{11}+a_{21}\leq\lambda_1\leq a_{12}+a_{22}\)が言えます。
計算すると、
\begin{eqnarray}
f\left( a_{12}+a_{22}\right)&=&\left( a_{12}+a_{22}\right)^2-\left( a_{11}+a_{22}\right)\left( a_{12}+a_{22}\right)+\left( a_{11}a_{22}-a_{12}a_{21}\right)\\
&=&a_{12}\left( a_{12}+a_{22}-a_{11}-a_{21}\right)\geq0,\\
f\left( a_{11}+a_{21}\right)&=&\left( a_{11}+a_{21}\right)^2-\left( a_{11}+a_{22}\right)\left( a_{11}+a_{21}\right)+\left( a_{11}a_{22}-a_{12}a_{21}\right)\\
&=&a_{21}\left( a_{11}+a_{21}-a_{12}-a_{22}\right)\leq0
\end{eqnarray}
です。
\(a_{12}+a_{22}\leq a_{11}+a_{21}\)のときも同様です。
命題3.の証明終わり
命題3.から、
$$
a_{11}+a_{21}<1,\quad a_{12}+a_{22}<1
$$
のときは、\(\lambda_1\)です。
故に、\(n=2\)の場合に定理0.の主張(2)が正しいことが分かりました。
皆様のコメントを下さい!
今回のジョークです。
無限の数の数学者がバーに入っていきます。
最初の1人はバーテンダーに近づいて「ラガーをパイントグラスで頼む。」と言いました。
後の人も全員「同じものを(すぐ前の人を指して)彼の半分だけ」と延々続けます。
するとバーテンダーは「ああもう。お前らみんな馬鹿だな。」と言って2パイントを注いだそうな。
これは、無限に同じことを繰り返すといつまで経っても終わらずにバーテンダーの気が滅入ってしまいますが、
\begin{eqnarray}
\sum_{n=0}^\infty\frac{1}{2^n}=1+\frac{1}{2}+\frac{1}{4}+\cdots=2
\end{eqnarray}
です。
それ故バーテンダーは一度に無限に居る全員分のビールを注いで「後は勝手にしろ」というわけです。
結
今回は、産業連関のレオンチェフ方程式について、\(n=1\)と\(n=2\)のときについて特に詳しく解説しました。
今回もグラフ理論のお話がありませんでしたが…
次回は一般のレオンチェフ方程式に対して数学的に踏み込んでみます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
グラフ理論についてより詳しく知りたい方は以下を参考にすると良いと思います!




コメントをする