「連結、グラフ距離、組み合わせグラフ、同型なグラフ」【幾何学の基礎シリーズ】グラフ理論編 その3

本記事の内容

本記事は、連結、グラフ理論、ループ辺、多重辺、組み合わせグラフについて解説する記事です。

本記事を読むにあたり、「グラフとは何か？」「路」について知っている必要があるため、以下の記事も合わせてご覧ください。

↓「グラフとは何か？」の記事

「グラフって何？〜クイズからイメージしよう〜(応用例も紹介！)」【幾何学の基礎シリーズ】グラフ理論編 その1

...

for-spring.com

2022.09.20

↓「路」についての記事

「有限グラフ、正則グラフ、路(みち)」【幾何学の基礎シリーズ】グラフ理論編 その2

...

for-spring.com

2022.09.21

連結

連結は本シリーズの最初にサラッと述べた通り、シンプルなコンセプトです。

「連結」を一言で。

一言で述べれば

ということです。
このコンセプトは前回解説した路でもって記述されます。

ちなみに、路とは以下でした。

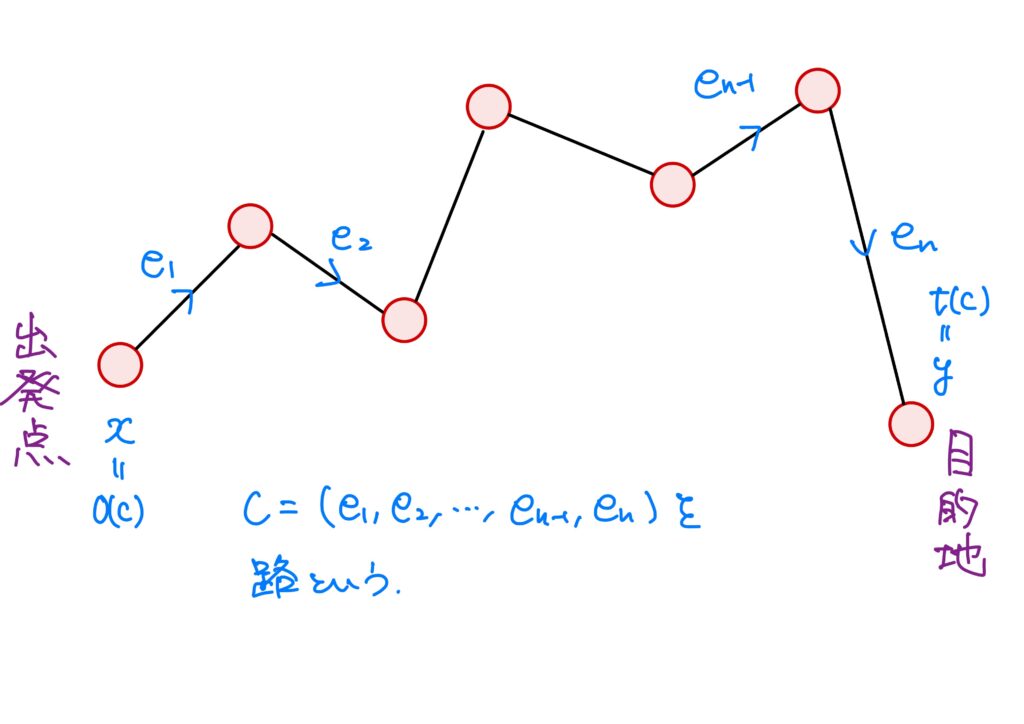
詳しくは【幾何学の基礎シリーズ】グラフ理論編 その2を御覧ください。

連結って何ですか？

では、「連結とは何か？」ということについて答えようと思います。

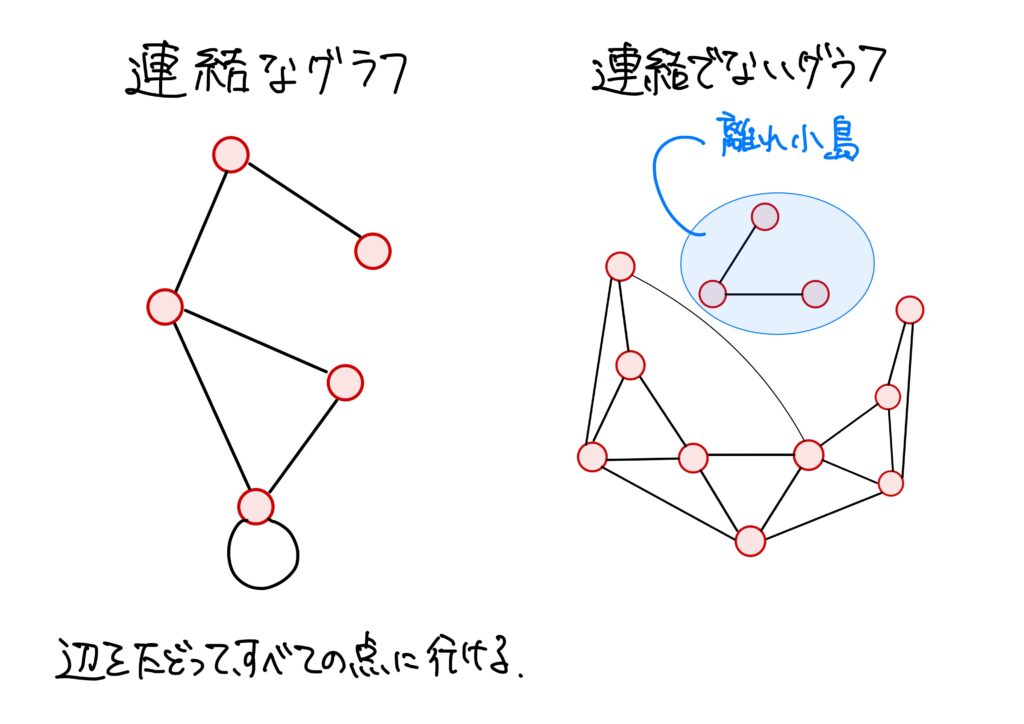
グラフの連結とはまさに、「どんな2点も”繋がっている”」という状態で、離れ小島が無い、ということです。

ちょっとした注意

連結を「どんな2点も”繋がっている”こと」と表現すると、「じゃあ、連結でないグラフは点だけ離れ小島のようになっているグラフということだな？」となるかもしれませんが、無向グラフについてはそれでOKです。
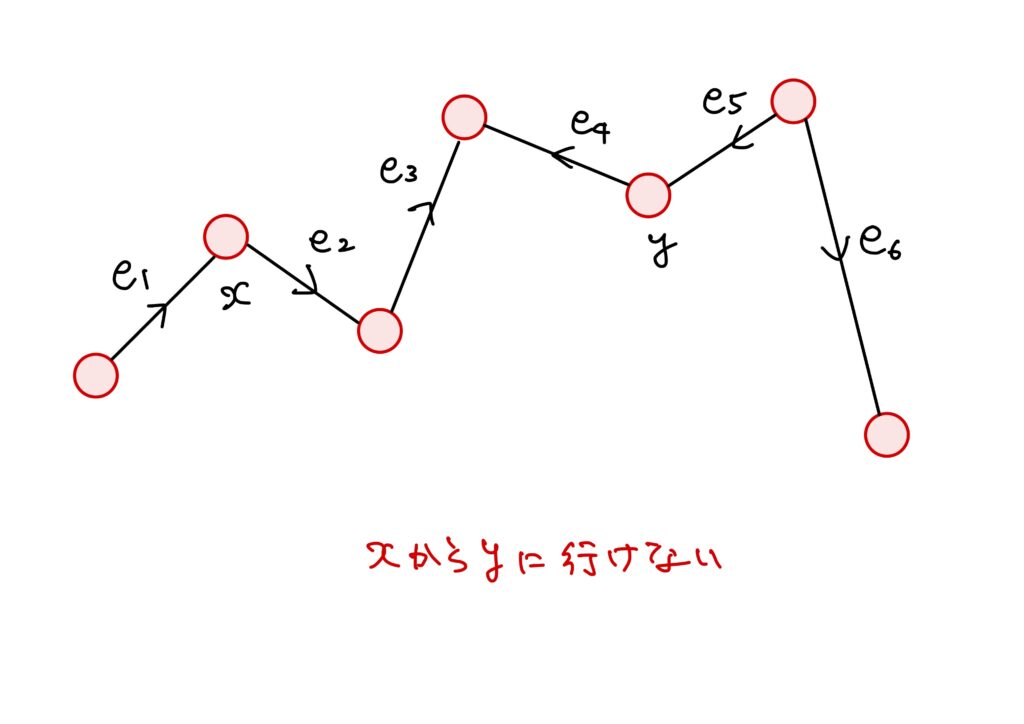
しかし、有向グラフについてはそうもいきません(後の記事で解説します)。

有向グラフでは、下図のように離れ小島がなくとも有向辺の向きによっては連結でない場合が考えられます。

連結のちょっとした性質

ここで、連結のちょっとした性質を紹介します。

命題1.の証明

集合$A\subset V$は空集合ではないので、ある要素$x\in A$が存在します。
グラフ$X=(V,E)$は連結なので、任意の$y\in V$に対して、
$$o(c)=x,\quad t(c)=y$$
を満たす路$c=\left( e_1,\dots,e_n\right)$が存在します。
$t(c)=y$ですので、$t(e_n)=y$と書き直すことが出来ます。
このとき、$y=t(e_n)\in A$が示されれば、証明完了です。

任意の$i\in\left\{1,\dots,n\right\}$に対して$y=t(e_i)\in A$であることを数学的帰納法で証明します。
$i=1$のときは、$o(e_1)=x\in A$です。
仮定から、
$$o(e)\in A\ \Longrightarrow\ t(e)\in A$$
ですので、$t(e_1)\in A$です。
故に、$i=1$のときは成り立ちます。

$t(e_i)\in A$と仮定しましょう。
このとき、$o(e_{i+1})=t(e_i)\in A$だから、これも
$$o(e)\in A\ \Longrightarrow\ t(e)\in A$$
により、$t(e_{i+1})\in A$です。
従って、全ての$i$に対して$t(e_{i+1})\in A$です。

命題1.の証明終わり

命題1.は連結なグラフの性質のうちの1つで、頂点の部分集合を取ってきたとき、その部分集合内で点が全て辺で繋がっていれば、その部分集合のとり方は元々のグラフの頂点の集合を取るしか無い、ということです。

グラフ距離

次に、グラフ距離について説明します。

距離関数

まずは、一般に「距離とは何か？」ということについてサラッとお話します。

「何を言っとるだ？」という感じかもしれませんが、最も馴染み深いと思われるユークリッド距離で考えるとイメージが湧きやすいと思います。

• 「$d(x,y)\geq0)であり、(d(x,y)=0\Leftrightarrow x=y$」という条件について
  これは、「距離は必ず$0$以上の値で、距離が$0$な点同士は同じ点しかありえない。」ということを表しています。
  「距離が負なんてことはありえないし、距離が$0$なのに点が違うってありえないでしょ」という直感に対応しています。
• 「$d(x,y)=d(y,x)$」という条件について
  これはそのまんまです。
  「$x$と$y$の距離と$y$と$x$の距離は同じだよね？」という直感に対応しています。
  東京駅から新宿駅までの距離と新宿駅から東京駅の距離は同じ、ということです。
• 「$d(x,y)+d(y,z)\geq d(x,z)$(三角不等式)」という条件について
  これは、三角形で考えると分かりやすいと思います。
  要するに、「三角形の2辺の長さの和は他の1辺の長さより大きい」ということです。

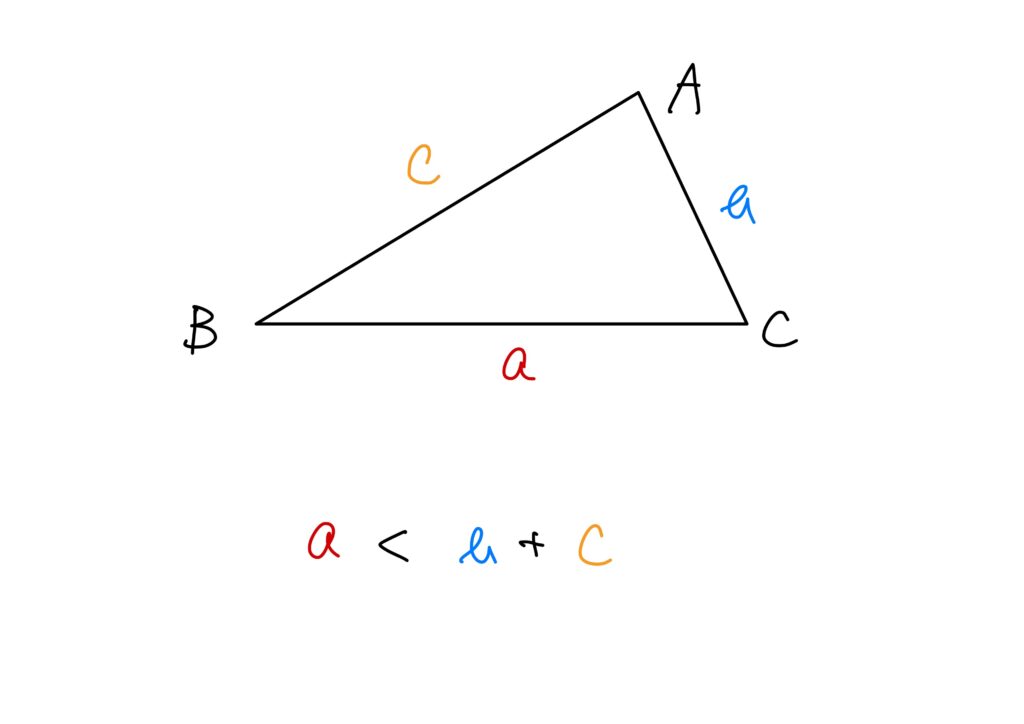
ちなみに、$\mathbb{R}^n$の距離関数(つまり$d:\mathbb{R}^n\times\mathbb{R}^n\to\mathbb{R}$)は、ユークリッド距離だけではありません。
先程の3つの条件を満たしさえすれば、距離と呼べる、という話だからです。
実際、$d:\mathbb{R}^2\times\mathbb{R}^2\to\mathbb{R}$を$(x_1,y_1),\ (x_2,y_2)\in \mathbb{R}^2$に対して
$$d(\boldsymbol{x},\boldsymbol{y})=\left|x_1-x_2\right|+\left|y_1-y_2\right|$$
と定めても、$d$は先の3つの条件を満たします(この$d$をマンハッタン距離といいます)。

余談(完備距離空間)

距離空間に付随する重要な概念として、完備距離空間というものがあります。
実数の連続性のシリーズで述べましたが、実数においてはコーシー列が収束します。
実は、一般にはコーシー列が収束するとは限りません(コーシー列は必ず収束します)。
実数の集合はユークリッド距離でもって距離空間となります。
このようにコーシー列が収束するような距離空間を完備距離空間といいます。
ちなみに、コーシー列が収束するように無理やり集合を”拡張”することを完備化といいますが、有理数の集合を完備化した集合が実数の集合です。
これは実は実数の連続性を担保しているともいえる事実です。

グラフ距離

連結なグラフに対しても距離を考えることが出来ます。
最もよく使われる(と筆者は思っています)がグラフ距離と呼ばれるものです。

要するに、最短経路です。

※注意※これは一般のグラフに対する距離ではなく、連結なグラフに対する距離ということです。

距離関数の節でも述べましたが、距離関数というのは1つの集合に対して1つしか存在しないわけでは有りません。
ちょっと限定的になってはしまいますが、グラフに対する距離としてハミルトン距離という距離もあります。

さて、「グラフ距離を”定める”って言ったって、本当にそれって距離関数なんですか？」となると思います。
そこで、先のグラフ距離が距離関数であることを証明します。

命題2.の証明

①$d(x,y)\geq0)であり、(d(x,y)=0\Leftrightarrow x=y$であることの証明

$x\neq y\in V$のとき、$|c|$は$x$と$y$をつなぐ辺の個数なので正の値です。
$d(x,y)$は$|c|$の最小値なので、$d(x,y)>0$です。

$x=y\in V$のときは$d(x,y)=0$と定めました。
故に、$d(x,y)\geq0$です。

②$d(x,y)=d(y,x)$の証明

$x$と$y$をつなぐ辺の個数の最小値と$y$と$x$とをつなぐ辺の個数の最小値は一致しているため$d(x,y)=d(y,x)$です。

③$d(x,y)+d(y,z)\geq d(x,z)$(三角不等式)

$x\neq y\in V$のとき、$d(x,y)+d(y,z)< d(x,z)$とすると、少なくとも1点、$y$の他に$x$と点$z$をつなぐ路に点が存在することになります。
しかし、これは路の長さの最小性に矛盾します。

$x=y$のとき、$d(x,y)+d(y,z)=0+d(y,z)=d(y,z)=d(x,z)$により成り立ちます。
$x=z$のとき、$d(x,y)+d(y,z)\geq0=d(x,z)$により成り立ちます。
$y=z$のときは$x=z$と同じです。

命題2.の証明終わり

組み合わせグラフ

本記事の最後に組み合わせグラフについて解説します。

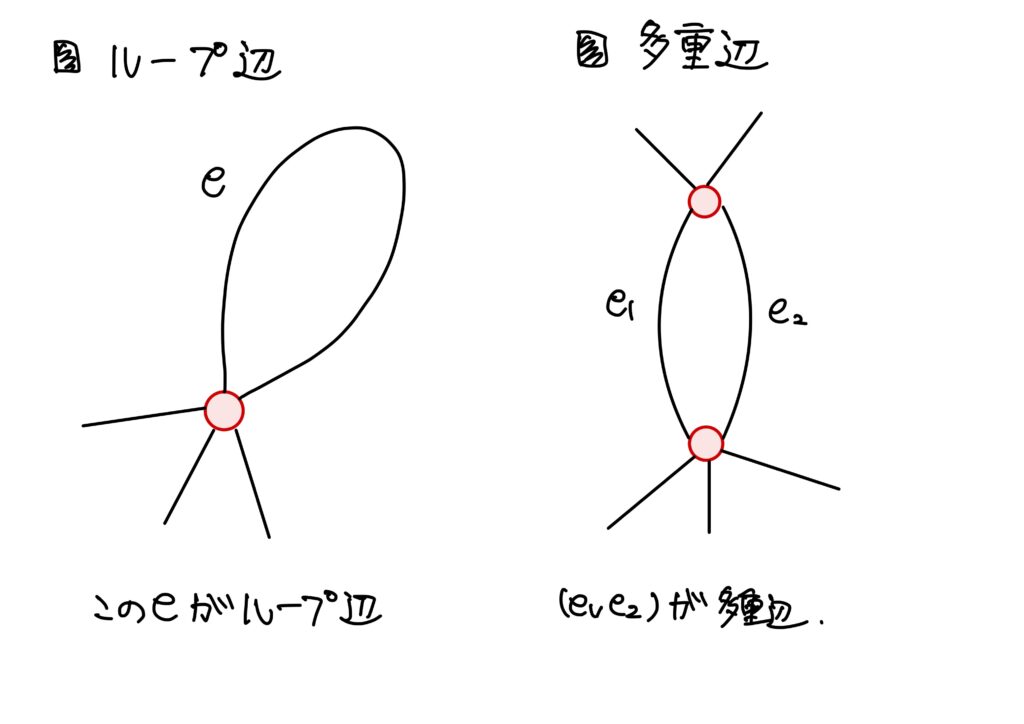
ループ辺と多重辺

簡単です。
辺の始点と終点が一致しているときに、その辺をループ辺といいます。
また、二点間に複数の辺が存在するときに、そのグラフは多重辺を持つと言われます。

組み合わせグラフ

簡単です。
ループ辺も多重辺も持たないようなグラフを組み合わせグラフといいます。

モデルとして利用する多くのグラフは有限で連結な組み合わせグラフです。

グラフを現象を表すモデルとして扱う場合、多くは有限で連結な組み合わせグラフ(これを助詞を除いて有限連結な組み合わせグラフといいます)です。

例えば、インターネットのネットワークでは、いくら端末が多くてもそれらは有限です。
世界中の端末を集めたとて、数は膨大ですが高々有限の個数しか存在しません。
当然、それらの端末をつなぐケーブルも有限個しか存在しません。
故にインターネットのネットワークのモデルは有限グラフです。
また、互いにケーブルで結ばれていない2つの部分に分けられるネットワークは考える必要がないので、対応するグラフは連結として良いわけです。
ループ辺に当たるケーブルは情報伝達において意味をなさないし、多重辺に当たるケーブルは1つのケーブルとして考えても差し支えありません。
故に、モデルになるグラフというのは組み合わせグラフということになります。

同型なグラフ

同型なグラフというのは「本質的には同じグラフ同士のこと」です。
“本質的に” とはどういうことかと言うと、それはグラフ理論の着眼点を考えると直ちに分かります。

前々回に

という話をしました。
つまり、一見形が異なろうが、点と点の繋がり方が同じであれば、同じですよね、という話です。

これを数学的に書くと以下です。

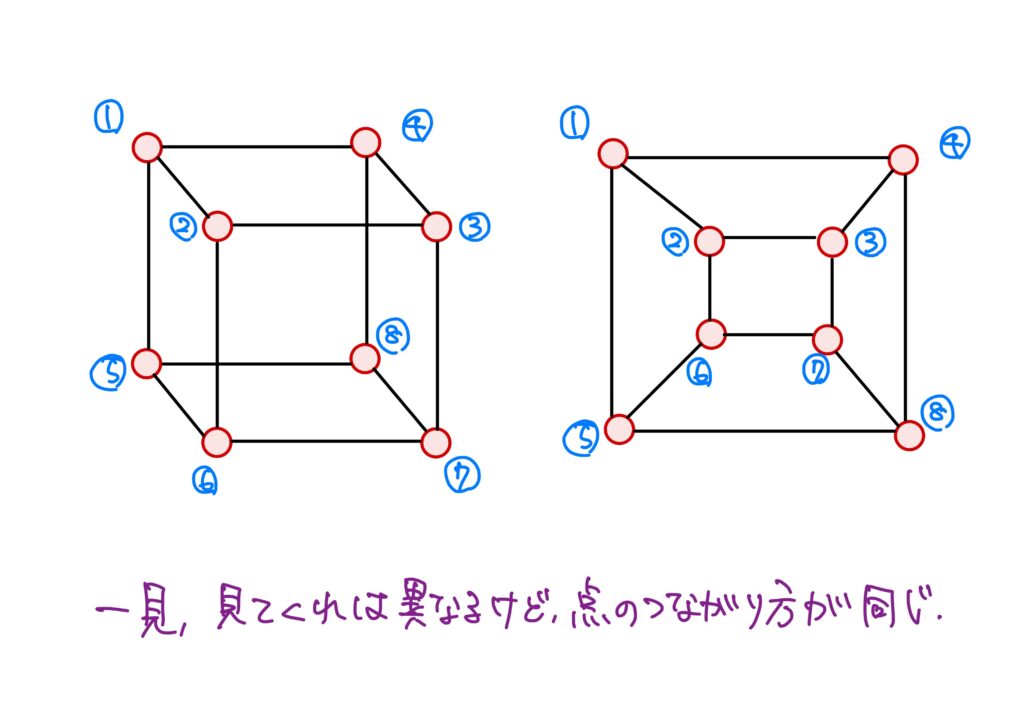
これらの条件はまさに2つのグラフの点の繋がり方が同じであることを表しています。
実際、

• $o\left( f_E(e)\right)=f_V\left(o(e) \right)$について
  これは、$e\in E_1$に対応する$X_2$の辺$f_E(e)\in E_2$の始点は、$e\in E_1$の始点に対応する$X_2$の始点と一致している、ということを述べています。
• $t\left( f_E(e)\right)=f_V\left(t(e) \right)$について
  これは、$e\in E_1$に対応する$X_2$の辺$f_E(e)\in E_2$の終点は、$e\in E_1$の終点に対応する$X_2$の終点と一致している、ということを述べています。
• $\overline{f_E(e)}=f_E(\bar{e})$について
  これは、$X_1$の各辺$e\in E_1$のに対応する$X_2$の辺$f_E(e)$の逆向きの辺は、$X_1$の各辺$e\in E_1$の逆向きの辺と対応する$X_2$の辺$f_E(\bar{e})$と一致している、ということを表しています。

皆様のコメントを下さい！

いきなり全く関係ない話をします。
筆者は漫画をそこそこ読むのですが、中でもバイブルと言えるのはBLEACHです。
もう大好きです。
何回読み直したか分かりません。
来月の10日から千年血戦篇のアニメが始まりますし、ワクワクです。

皆様のバイブル的な漫画は何ですか？是非コメントで教えて下さい！

結

今回は、連結、グラフ距離、組み合わせグラフ、同型なグラフについて解説しました。
それぞれ

• 連結：グラフのどの2点も路で繋がっている状態。
• グラフ距離：グラフの2点間の最短経路。
• 組み合わせグラフ：ループ辺も多重辺も無いグラフ。
• 同型なグラフ：見てくれは違えど、点と点との繋がり方が一致しているグラフ同士。

です。

次回は有向グラフと隣接行列①ということで、それぞれを導入します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！