本記事の内容
本記事は、グラフ理論の応用の1つである産業連関について解説する記事です。
本記事を読むにあたり、グラフについて知っている必要があるため、以下の記事も合わせてご覧ください。
本題に入る前に…
本題に入る前に、本記事では産業連関について解説しますが、今回は数学のお話は殆どありません。
むしろ経済学的なお話です。
ただ、筆者は経済学が専門というわけではありませんので、その点厳密性は欠いているかもしれません。
とはいえ、数学に関連する部分については厳密に記述します。
本記事で述べることは、要するに
です。
ほんのちょっと経済学(読み飛ばしてOK)
経済学を一言で述べれば
です。
「経済学」を知りたいのに「経済」という言葉を使ってしまっているので、違和感があるかもしれませんが、経済学の説明としては間違っていません。
経済という言葉は、国を治め人民を救うという意味の「経国済民」から派生しています。
学問的には、人言共同体の基礎をなす財・サービスの生産・分配・消費の行為、ならびにその過程、またそれを通じて形成される人間の間の社会的関係の総体を意味します。
余談①
1932年発刊のライオネル・ロビンズ著『経済学n本質と意義』では「他の用途を持つ希少性のある経済資源と目的について人間の構想を研究する科学が経済学である」と述べられているようです。ここで、財というは、人間の物質的・精神的生活にとって、何らかの効用をもつものです。
先の「経済学とはなにか?」の答えから更に具体的な内容に踏み込めば、「国を治め、人民を救う」のには、どのような経済システムが望ましいのだろうか?という「政治的」な問題に立ち入ることになり、研究者の世界観やら価値観、場合によってはイデオロギーの違いによって異なる見解が生じます。
例えば、
- マルクス経済学:唯物論を基礎としている。
- ケインズ学派:有効需要(マクロ経済全体で見た需要のことで、消費、投資、政府支出及び純輸出(輸出-輸入)の和のこと)の考え方を根幹とする需要政策中心。
- サプライサイドの経済学:経済活動のうち、供給面を重視。
があります。
本記事では経済モデルに商店を絞って、「世界観」やら「価値観」やらが入り込む問題は扱いません。
つまり、経済現象を「あるがままの」視点で見ますよ、ということです。
実は、次回解説するレオンチェフ方程式には以前証明したペロン-フロベニウスの定理が役立ちます。
※ペロン-フロベニウスの定理は【幾何学の基礎シリーズ】グラフ理論編 その9を御覧ください。
産業連関について
ある経済システム(例えば特定の国)の特定期間(会計年度)において、このシステムに属する産業部門(production sector)が生産したものを部門を通じて共通なユニットで測ります。
測ったものを生産量と言います。
通常は量を金額に換算するのですが、ことではユニットを使います。
というのも、金額に換算するというのは、ある種当然のことなのですが、生産物は形を帰るので、それをそのまま指標として使うことは出来ないからです。
産業連関表
多数の業種からなる国内産業間の需要・供給の関係及び消費者、政府、供給国と国内産業間の需要・供給の関係を産業連関表(Input-Output Table, I/O Table)で表します。
都道府県の産業連関表やら、全国を地域ブロック別に扱う地域間産業連関表もあり、地域の現実を反映した分析を行うことも出来ます。
さらに、日本・米、日・アジア、日・米・EU・アジアなど、各国の産業連関表を拡張、統合化した国際産業連関表もあって、国際分業や交易関係が作るグローバルなネットワークを定量的に把握することも出来ます。
ただし、経済学では、企業を「何かを入れると何かが出てくる」というブラックボックスのようにみなして、生産活動の内容には触れないことにします。
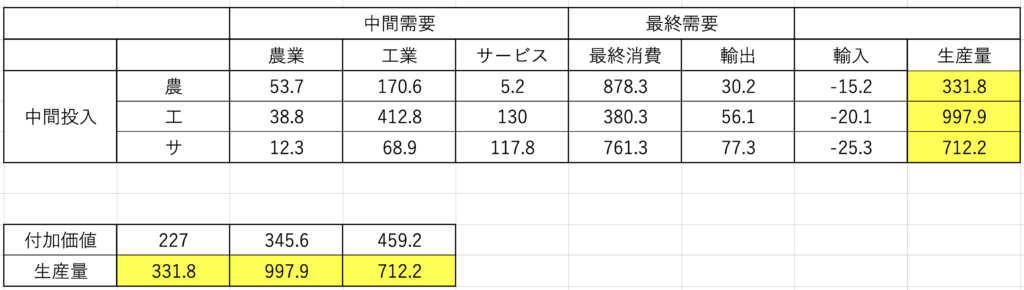
上記の表は産業連関表の例です。
単純化するために、産業の部門は農業(agriculture)、工業(industry)、サービス(service)の3種類としています。
農業は第一次産業、工業は第二次産業、サービスは第三次産業と呼ばれます。
また、各産業の部門は1種類の生産物を扱うと仮定しています。
勿論、実際の産業連関表では、多数の部門を扱う必要があります。
産業連関表の各種用語について
- 中間需要(intermediate demand)
他の産業の生産活動で必要とされる原材料や燃料として販売された財・サービスのこと。
内部需要(internal demand) ともいう。 - 中間投入(intermediate input)
各産業部門の生産過程で原材料、燃料等の経費として投入される費用のこと。
内部投入(internal input)ともいう. - 最終需要(final demand)
産業部門以外の部門(世帯,政府,外国部 門など)に対する需要のこと。
外部需要(external demand)ともいう。 - 最終消費(final consumption)
家計消費,政府消費,国内資本形成などを指す。 - 付加価値(added value)
雇用者所得,営業余剰,間接税などを指す。
産業連関表の読み方
先の産業連関表において、色付きの部分異界の数字を横(行)と縦(列)ごとに足したものが色付きの数字に等しいことを確かめましょう。
行の読み方
産業連関表を再掲しておきます。

農業の行(第1行)は、農業の1年間の生産額の「使われ方」を示しています。
ほかも同様です。
最後のマスにある生産量がそれ以前のマスにあるがくの総和になっていることに注意しましょう。
つまり
- 農業部門の生産高331.8ユニット、
それが
- 農業自身に53.7ユニット、
※1つの部門の供給が、それ自身になされることもあります。
例えば、発電所が発電した電気を自分自身で使ったり、生産した農作物の種から新たに農作物を生産したりする場合です。 - 工業部門に170.6ユニット、
- サービス部門に5.2ユニット、
が受容されて使われ、このほか
- 最終消費財として国内で87.3ユニット、
- 海外(輸出)で30.2ユニット
のそれぞれ需要されて使われることを示しています。
注意すべきなのは、需要の合計は347ユニットであるのに、国内生産に依る供給は331.8しかないことです。
不足分の15.2ユニットは、海外から(輸入)供給されるほかありません。
輸入の15.2ユニットはこのことを表しています。
言い換えれば、第一行は
$$
53.7+170.6+5.2+87.3+30.2-15.2=331.8
$$
ということを表しています。
列の読み方
産業連関表を再掲しておきます。

次に農業の列(第1列)を見てみましょう。
- 農業の生産量から53.7ユニット、
- 工業の生産量から38.8ユニット,
- サービス業の生産量から12.3ユニット
を使って331.8ユニットの生産をしています。
これを総量(\(53.7+38.8+12.3\))でいうと、合計は104.8ユニットの生産量をを331.8ユニットの生産物に変えている、というのが農業における今年度の生産活動です。
もっと言い換えれば、農業の生産活動は104.8ユニットなのに、227.0ユニットだけ価値を加えている、ということになります。
他の列も同様です。
このように、各産業の生産活動によって生み出される価値、すなわち付加価値がこの第3行に書かれています。
つまり第1列は
$$
53.7+38.8+12.3+227.0=331.8
$$
ということを表しています。
具体的な数値の代わりに記号を使って表現してみます。
具体的な数値の代わりに、記号を使うことにしましょう。
むしろこの方が何を問題にしているかがわかりやすいし、現実のデータから経済活動の本 質的な構造を読み取り,この構造を表現する数学的モデルを構築するためにも重要なステップです。
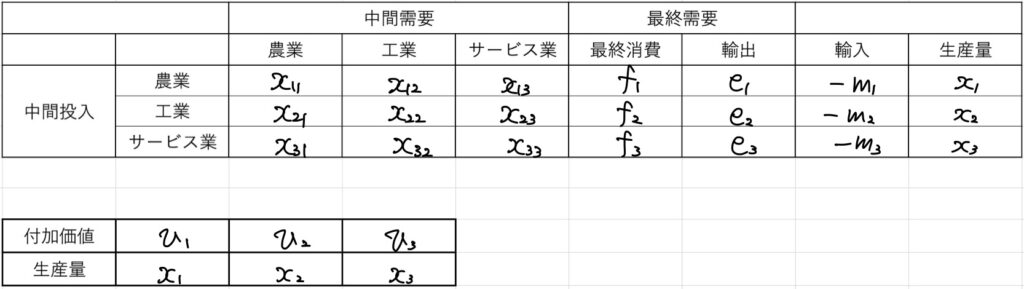
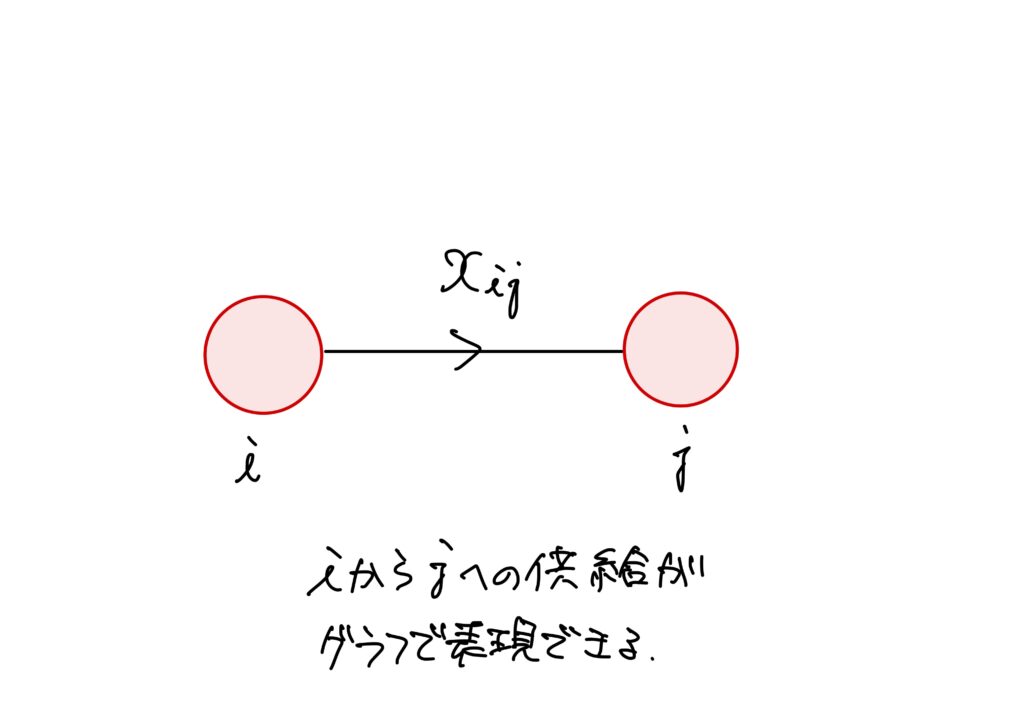
上記の表において、農業部門には1、工業部門には2、サービス部門には3の数字を当てています。
このとき
- \(x_i\):部門\(i\)の生産量
- \(x_{ij}\):部門\(i\)の生産量から部門\(j\)により需要され、使われる量
- \(f_i\):部門\(i\)の生産量から消費財として需要され使われる量
- \(e_i\):部門\(i\)の生産量から海外(輸出)のために需要され、使われる量
- \(m_i\):部門\(i\)に輸入で海外から供給される量
とします。
ただし、ユニットは省略しています(以降、ユニットは省略します)。
行と列が表しているもの
行で表しているのは、部門\(i\)における生産量とほかからの需要量との「釣り合い」であり、需要量に見合った生産を行った場合、
$$
x_{i1}+x_{i2}+x_{i3}+f_i+e_i-m_i=x_i
$$
が成り立っています。
列では、
$$
x_{1j}+x_{2j}+x_{3j}+v_j=x_j
$$
が成り立っています。
故に、正の付加価値が付けられるのであれば、
$$
x_{1j}+x_{2j}+x_{3j}<x_j\tag{1}
$$
です。
最終需要量から輸入量を引いたもの
最終需要量(最終消費と輸出)から輸入量を引いたもの
$$
b_i=f_i+e_i-m_i
$$
は正か\(0\)です。
投入係数
産業連関表から投入係数を計算してみます。
「投入係数」\(a_{ij}\)は、部門\(j\)において、その生産量(\(x_j\))に対して、部門\(i\)から生産量をどれくらい必要としたのか?という比率です。
つまり、
です。
更に言い換えれば、部門\(j\)における生産量1ユニット当たりの部門\(i\)への需要量(\(i\)から\(j\)への供給量)が投入係数\(a_{ij}\)であり、これを比例定数として、\(i\)への需要量が\(j\)における生産量に比例している、というわけです。
この比例定数は各業種の特性を表している、と考えます。
より詳しく言えば、\(a_{ij}\)は生産技術(生産現場技術だけでなく調達・流通・組織管理なども含めた経済活動全体の技術)によって決定されます。
この生産技術は長期間では向上する可能性がありますが、短期間(例えば5年程度)では一定と考えられるます。
従って、ある年度で経済統計から得られた投入係数(以下の表)は、この年度以降の生産額には依らないと仮定してOKです。
| 部門 | 1 | 2 | 3 |
| 1 | \(a_{11}=0.16\) | \(a_{12}=0.17\) | \(a_{13}=0.01\) |
| 2 | \(a_{21}=0.12\) | \(a_{22}=0.41\) | \(a_{23}=0.18\) |
| 3 | \(a_{31}=0.04\) | \(a_{32}=0.07\) | \(a_{33}=0.17\) |
先程の例で概算で投入係数を求めると上記の表が得られます。
\(x_1,x_2,x_3\)と\(b_1,b_2,b_3\)の間の関係式
\(x_1,x_2,x_3\)と\(b_1,b_2,b_3\)の間の関係式を表せば、次の関係式を得ます。
\begin{eqnarray}
&&a_{11}x_1+a_{12}x_2+a_{13}x_3+b_1=x_1\\
&&a_{21}x_1+a_{22}x_2+a_{23}x_3+b_2=x_2\\
&&a_{31}x_1+a_{32}x_2+a_{33}x_3+b_3=x_3
\end{eqnarray}
これを見ると連立方程式ですね。
皆様のコメントを下さい!
今回のジョークです。
ある数学者とその親友である技術者は13次元空間の幾何学に関する公開講義に参加しました。
講義の後で「13次元はどうだった?」と数学者が訊ねると、技術者は「ああ、なんだか眩暈がしてきちゃったよ」と告白し、「君は13次元空間をどうやって理解するの?」と聞き返した。
数学者は「ああ、それは簡単。まず\(n\)-次元空間で一般論を作って、\(n\)に13を代入すればいいんだよ」と答えました。
これは、数学者が個々の事例から一般へという帰納的に物事を考えるよりも、「一般から特殊へ」という流れで物事を考える傾向がある、といことを述べている話です。
数学者は一般化が大好き、ということです。
結
今回は、産業連関について解説しました。
今回はグラフ理論のお話がありませんでしたが、産業連関はグラフ理論が応用される分野であるため、その解説の準備をしました。
経済学も数学の知識を使うことであらゆる事がわかります。
次回は産業連関を実際に数学で考えてみます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
グラフ理論についてより詳しく知りたい方は以下を参考にすると良いと思います!




コメントをする