「部門数が一般の場合のレオンチェフ方程式〜グラフ理論の応用(産業連関④)〜」グラフ理論編  その15

本記事の内容

本記事は、部門数が一般の場合のレオンチェフ方程式(一般の均衡産出高モデル)について解説する記事です。

本記事を読むにあたり、レオンチェフ方程式、部門数が1個と2個の場合のレオンチェフ方程式について知っている必要があるため、以下の記事も合わせてご覧ください。

↓レオンチェフ方程式の記事

「レオンチェフ方程式〜グラフ理論の応用(産業連関②)〜」【幾何学の基礎シリーズ】グラフ理論編 その13

...

for-spring.com

2022.10.08

↓部門数が1個と2個の場合のレオンチェフ方程式の記事

「部門数が1個と2個のレオンチェフ方程式〜グラフ理論の応用(産業連関③)〜」グラフ理論編 その14

...

for-spring.com

2022.10.11

今回、次回、次次回の目標

今回、次回、次次回の目標は次の定理を証明することです。

今回は定理0.の(1)を証明します。

定理0.の$n=1,2$の場合は【幾何学の基礎シリーズ】グラフ理論編 その14を御覧ください。

レオンチェフ方程式の軽い復習

レオンチェフ方程式について軽く復習します。

産業連関表

以下の表を産業連関表といいます。

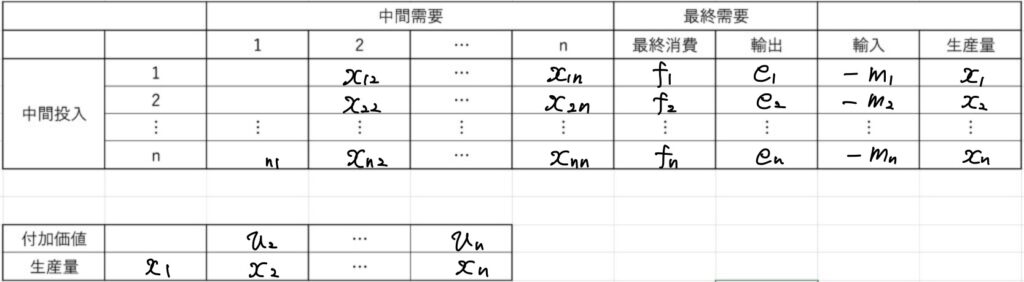
レオンチェフ方程式

ある年度の産業連関表が上記のように与えられたとします。

投入係数を$a_{ij}$、すなわち部門$i$からの生産量の内、部門$j$に需要されて使われる量は$x_{ij}=a_{ij}x_j$とします。
ただし、$a_{ij}=0$の場合は、$i$から$j$には供給が無い、と考えます。
部門$i$にシステムの外部から需要される量は$b_i=f_i+e_i-m_i$です。
従って、需要量に見合った生産が行われたのであれば、一般の場合も次の等式を得ることが出来ます。

$$\begin{eqnarray} x_1&=&a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n+b_1\\ x_2&=&a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n+b_2\\ \tag{\(\ast\)} \vdots&&\quad\vdots\qquad \quad\vdots\qquad\quad\qquad\quad \vdots\quad \quad\vdots\\ x_n&=&a_{n1}x_1+a_{n2}x_2+\cdots+a_{nn}x_n+b_n\\ \end{eqnarray}$$

ここで、右辺が需要量、左辺が生産量を表しています。

この等式を、$a_{ij}\geq0$が予め与えられたとき(これも投入係数呼ぶことにしますが、不等式(2)は仮定しません)、最終需要料(厳密には輸入量を引いたもの)$b_1,\dots,b_n\ (b_i\geq0)$に対して、それに見合う生産量(均衡産出高)$x_1,\dots,x_n\ (x_i\geq0)$を求める連立方程式と見ます。
要するに、$a_{ij}\geq0$が与えられたときに、$b_1,\dots,b_n\ (b_i\geq0)$に対して$x_1,\dots,x_n\ (x_i\geq0)$を求める連立方程式と見る、ということです。

この方程式$(\ast)$をレオンチェフ方程式あるいは均衡産出高モデルと言ったのでした。

もし、正の付加価値が付けられるならば、更に不等式
$$a_{1j}+a_{2j}+\cdots+a_{nj}<1\tag{\(\ast\ast\)}$$
が成り立ちます。

viable

詳しくは、【幾何学の基礎シリーズ】グラフ理論編 その13を御覧ください。

一般の均衡産出高モデルに入る前に…(記号のお話)

産業連関表の投入係数表から得られる投入係数行列を
$$A=\begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{pmatrix}$$
とします。
$$\boldsymbol{x}= \left( \begin{array}{c} x_1\\ x_2\\ \vdots\\ x_n \end{array} \right),\quad \boldsymbol{b}= \left( \begin{array}{c} b_1\\ b_2\\ \vdots\\ b_n \end{array} \right)$$
とすると、レオンチェフ方程式$(\ast)$は
$$\boldsymbol{x}=A\boldsymbol{x}+\boldsymbol{b}\tag{1}$$
と表現できます。

一般に、ベクトル$\boldsymbol{a}$の成分がすべて非負なときは$\boldsymbol{a}\geq0$と表現することにして、非負ベクトルと呼ぶことにします。
ベクトル$\boldsymbol{a}$の成分が全て正であれば、$\boldsymbol{a}>0$と表して、正ベクトルと呼びます。
行列についても同様にして、非負行列、正行列と呼びます。
投入係数行列$A$は非負な正方行列です。

簡単な事実

ここで、簡単な事実を数個証明します。

命題1.の証明

ベクトル$A\boldsymbol{x}$の第$k$成分は
$$\sum_{j=1}^ma_{kj}x_j$$
です。
$a_{kj}\geq0$で、任意の$k,j$に対して同時に$a_{kj}=0$となることはありません。
そして、$\boldsymbol{x}>0$ですので、$x_j>0$です。
故に、$A\boldsymbol{x}>0$です。

命題1.の証明終わり

次は久しぶりのグラフ理論の話です。

命題2.の証明

$A=\left( a_{ij}\right)$とするとき、$A^\nu$の$(i,j)$成分$a_{ij}^{(\nu)}$は
$$\sum_{i_1,\dots,i_{\nu-1}}a_{ii_1}a_{i_1i_2}\cdots a_{i_{\nu-1}j}$$
であることを思い出しましょう。
$a_{ij}^{(\nu)}>0$であるための必要十分条件は、
$$(i,i_1),\ (i_1,i_2),\ \dots,(i_{\nu-1},j)$$
が全て$X^o$の有向編と成るような$i_1,\dots,i_{\nu-1}$が存在することです。
言い換えると、$i$を始点として、$j$を終点とするような長さ$\nu$の路が存在する、ということです。

命題2.の証明終わり

$A$が非負正方行列、$\boldsymbol{b}>0$ならば(1)は解$\boldsymbol{x}\geq0$を持つか？

以下、$A$は非負行列とするだけで、産業連関表から得られる投入係数行列とは仮定しません。
要するに、一般論を述べる、という話です。

問題

さて、問題は

ということです。
(1)を書き直せば、
$$\left( I-A\right)\boldsymbol{x}=\boldsymbol{b}$$
と表すことが出来ます。
ただし、$I$は単位行列です。
もし、$I-A$が逆行列$\left( I-A\right)^{-1}$を持てば、
$$\boldsymbol{x}=\left(I-A \right)^{-1}\boldsymbol{b}$$
となって、解$\boldsymbol{x}$が求まります。
しかしながら、次の問題が生じます。

1. $I-A$は逆行列を持つか？
2. 仮に$I-A$が逆行列$\left( I-A\right)^{-1}$を持ったとて、$\left( I-A\right)^{-1}\boldsymbol{b}\geq0$か？
3. 理論的には意味があっても、行列$A$のサイズは大きくて(例えば次数が500、つまり産業連関の部門が500個)、現実的に計算可能か？

問題3.について

問題3.についてはコンピュータを使えばOKです。
実際、パッケージ化された計算ソフトが存在します。

問題1.について

viable(実行可能)とは何だったか、ということを確認します。

$A$がviableであれば、$I-A$は逆行列を持ちます。
実際、第$i$成分が$1$、他の成分が$0$であるような基本ベクトル$\boldsymbol{e}_i$に対して、$\boldsymbol{e}_i$は非負ベクトルだから、$\left( I-A\right)\boldsymbol{x}_i=\boldsymbol{e}_i$となるベクトル$\boldsymbol{x}_i$が存在します。
故に、$\left( I-A\right)$には逆行列が存在します。

ちなみに、$I-A$の逆行列$\left( I-A\right)^{-1}$はレオンチェフ逆行列といいます。

余談(不動点)

$n$変数関数の$n$個の系 $$\boldsymbol{f}(\boldsymbol{x})=\left(f_1(x_1,\dots,x_n),\dots,f_n(x_1,\dots,x_n) \right)$$ が与えられたとき、$\boldsymbol{x}=\boldsymbol{f}(\boldsymbol{x})$となる$\boldsymbol{x}$を$\boldsymbol{f}$の不動点といいます。
上の方程式は$\boldsymbol{f}(\boldsymbol{x})=A\boldsymbol{x}+\boldsymbol{b}$により定められる関数系の不動点を求める問題だ、と考えることが出来ます。
一般の関数系に対する不動点の概念と、ある条件下に不動点の存在を主張する不動点定理は、一般均衡(general equilibrium)の理論で用いられています。
一般均衡理論は、「変動している現実の状態にある位置自転で止め、条件を固定化し、競争を徹底的に行うと、社会全体がこれ以上変化しない均衡状態に至る。」というアイデアに基づいています。
レオン・ワイラスが19世紀に創始して、1950年代にケネス・アロー、ジェラール・ドブルー、ライオネル・マッケンジー、二階堂副包らの貢献で現在の整合的な分析手法となりました。

問題2.について

問題2.が解決できるか、ということにたいして基本的な役割を果たす事実を述べます。

補題3.の証明

$k$についての数学的帰納法で証明します。
$k=1$のときは、(1)そのものです。
$k=n$のときに成り立つと仮定します。
つまり、以下を仮定します。
$$\boldsymbol{x}=A^n\boldsymbol{x}+A^{n-1}\boldsymbol{b}+A^{n-2}\boldsymbol{b}+\cdots+A\boldsymbol{b}+\boldsymbol{b}$$
この両辺に左から$A$を掛けると、
$$A\boldsymbol{x}=A^{n+1}\boldsymbol{x}+A^{n}\boldsymbol{b}+A^{n-1}\boldsymbol{b}+\cdots+A\boldsymbol{b}+A\boldsymbol{b}$$
となります。
両辺に$\boldsymbol{b}$を加えれば、
$$A\boldsymbol{x}+\boldsymbol{b}=A^{n+1}\boldsymbol{x}+A^{n}\boldsymbol{b}+A^{n-1}\boldsymbol{b}+\cdots+A\boldsymbol{b}+A\boldsymbol{b}+\boldsymbol{b}$$
が得られて、$A\boldsymbol{x}+\boldsymbol{b}=\boldsymbol{x}$だから、これは$k=n+1$に対しても正しい、ということを示しています。

補題3.の証明終わり

定理0.の(1)の証明

今までのことを使って、定理0.の(1)を証明します。

定理0.の(1)の証明

$$\begin{eqnarray} &&B_k\left( b_{ij}^{(k)}\right)=A^{k-1}+\dots+A+I,\\ &&B_k\boldsymbol{b}=\boldsymbol{c}_k=\left( c_i^{(k)}\right) \end{eqnarray}$$
としましょう。
$A^k\boldsymbol{x}$、$B_k\boldsymbol{b}$の成分は全て非負だから、(2)により全ての$i,j$に対して
$$x_i\geq c_i^{(k)}-\sum_{j=1}^nb_{ij}^{(k)}b_j\geq b_{ij}^{(k)}b_j$$
が成り立ちます。
このことから、$B_k$の成分は全て有界です。
さらに、$B_k$の各成分は$k$に関して増加列です。
故に、
$$B=\lim_{k\to\infty}B_k$$
という$B$が存在します。
$A^k=B_{k+1}-B_k$に注意すると、収束列の隣り合う2項の差は$0$に収束するので、
$$\lim_{k\to\infty}A^k=O$$
です。
故に
$$B\left( I-A\right)=\lim_{k\to\infty}B_k\left( I-A\right)=\lim_{k\to\infty}\left( I-A^k\right)=I$$
となるので、$I-A$は$B$を逆行列として持ちます。
次に$\boldsymbol{b}\geq0$を任意に取ります。
$B=\left( I-A\right)^{-1}$により、$\boldsymbol{x}=B\boldsymbol{b}$とすると、$\boldsymbol{x}$はレオンチェフ方程式$\boldsymbol{x}=A\boldsymbol{x}+\boldsymbol{b}$の一意的な解です。
$B$は非負行だから、$\boldsymbol{x}=B\boldsymbol{b}\geq0$です。
従って、解は非負ベクトルです。

定理0.の(1)の証明終わり

皆様のコメントを下さい！

今回のジョークです。

これは、数学者は物理現象を扱わないため、社会に興味を持たない傾向があることを笑ったジョークだそうです。
しかし、現代の数学は自然現象を記述する言語としての側面が強くなっているため、物理現象に深い興味を示す数学者も数多くいる印象があります。
そういう意味ではこのジョークは極端かな、とも思います。

結

今回は、産業連関のレオンチェフ方程式について、一般の場合のレオンチェフ方程式を導入しました。
そして、投入係数行列がviableであるための十分条件を与えました。

次回は一般のレオンチェフ方程式にの投入係数行列のviabilityの判定法について解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

グラフ理論についてより詳しく知りたい方は以下を参考にすると良いと思います！