本記事の内容
本記事は、ペロン-フロベニウスの定理の証明のための準備をする記事です。
本記事を読むにあたり、行列の固有値、既約について知っている必要があるため、以下の記事もあわせてご覧ください。
↓固有値の記事(シリーズ化しているため一部を掲載しています)
↓既約の記事
ペロン-フロベニウスの定理って何?
結論から先に述べます。
ペロン-フロベニウスの定理とは以下です。
ただし、ベクトル\(\boldsymbol{x}\)に対して\(\boldsymbol{x}\geq0\)と書いたらば、\(\boldsymbol{x}\)のすべての成分が\(0\)以上だ、という意味です。
定理0.(Perron-Frobeniusの定理)
成分がすべて非負な既約\(n\)次正方行列\(A=\left(a_{ij} \right)\)は\(A\neq O\)であるとき、次の性質を満たす固有値\(\lambda(A)\)を持つ。- \(\lambda(A)>0\)であり、\(\lambda(A)\)は特性根として単根である。さらに成分が正の固有ベクトルを持つ。
- \(A\)の任意の固有値\(\lambda\)について、\(\left|\lambda\right|\leq \lambda(A)\)が成り立つ。すなわち\(\lambda(A)\)は\(A\)の最大な正の固有値である。
- \(A\boldsymbol{x}=\lambda\boldsymbol{x}\)、\(\boldsymbol{x}\geq0\)、\(\boldsymbol{x}\neq\boldsymbol{0}\)であるとき、\(\lambda=\lambda(A)\)かつ\(\boldsymbol{x}>0\)が成り立つ。
- \(\displaystyle\min_{j=1,\dots,n}\sum_{i=1}^na_{ij}\leq\lambda(A)\leq\max_{j=1,\dots,n}\sum_{i=1}^na_{ij}\)、\(\displaystyle\min_{i=1,\dots,n}\sum_{j=1}^na_{ij}\leq\lambda(A)\leq\max_{i=1,\dots,n}\sum_{j=1}^na_{ij}\)
このペロン-フロベニウスの定理は次回証明します。
ペロン-フロベニウスの定理のちょっとした小咄
定理0.の主張を見ると、「グラフ理論と関係ないんじゃない?」と思われるかもしれません。
しかし、グラフ理論としっかり関係しています。
というより、ペロン-フロベニウスの定理はグラフ理論だけでなく、ありとあらゆる分野で応用されています。
数値解析、確率論、経済学など様々です。
マルコフ(Markov)連鎖
本節では確率論のマルコフ連鎖についてちょっとだけお話します。
ただ、イメージをお話するだけで、厳密なお話はしません。
「ほーん。そーなんだー。」くらいで読んでいただければと思います。
確率論におけるマルコフ連鎖(Markov chain)とは、有限この状態を持ち、離散的な単位時間に一定の確率で次の状態にうつるような確率過程(時間とともに変動する偶然現象を記述するための数学モデル)です(可算無限個の状態をもつものや連続時間のものもありますが、ここでは考えません)。
\(X_1,\dots,X_n\)を状態として、モノが状態\(X_j\)から状態\(X_i\)へうつる確率が\(p_{ij}\)だとします。
この\(p_{ij}\)を成分とする行列\(A=\left( p_{ij}\right)\)を考えます。
状態\(X_i\)のモノが\(v_i\)個あるとし、ベクトル\(\boldsymbol{v}=\left( v_1,\dots,v_n\right)^\top\)とします。
このとき1単位時間後の状態というのは\(A\boldsymbol{v}\)です。
同様にして、\(k\)単位時間後の状態は\(A^k\boldsymbol{v}\)です。
マルコフ連鎖における状態は\(A\)の固有値\(1\)に対する固有ベクトルです。
この様子を記述するためにペロン-フロベニウスの定理が用いられます。
Googleの検索エンジン
Google の検索エンジンのランキング手法(Google PageRankの原理)にもペロン-フロベニウスの定理が間接的に使われています。
検索エンジンのランキングシステムは検索ワードにマッチするウェブページを重要なものから順に並べ
るための方法です。
その中でもGoogle PageRankはウェブをマルコフ連鎖をモデル化して、その定常な状態を計算することでランキングを計算しています。
この計算は本質的には大規模行列の固有値計算です。
この部分にペロン-フロベニウスの定理が使われています。
グラフ理論への応用例
離散スペクトル幾何という分野では「隣接行列の固有値、固有ベクトルとグラフの幾何学的、グラフ理論的性質との間にある関係を調べる」ということが大きなテーマの1つになっています。
要するに、グラフを上手く表現している隣接行列の固有値を調べることでグラフをより深く理解しよう、ということで、これにペロン-フロベニウスの定理が用いられています。
ペロン-フロベニウスの定理はグラフ理論的視点でを含みます。
ペロン-フロベニウスの定理は行列の固有値に対する事実ですが、実はその行列を隣接行列として捉えることでグラフ理論の視点を入れることが出来ます。
今回は非常に応用が効くペロン-フロベニウスの定理のの証明の準備を行います。
ペロン-フロベニウスの定理を確かめてみます。
前回証明した以下の定理を使います。
定理1.
与えられた\(n\)次の正方行列\(A=\left( a_{ij}\right)\)が可約であれば、添字の番号を並べ替えることにより、次の行列に変形することが出来る。 $$ \begin{pmatrix} A_1&\ast&\ast&\cdots&\ast\\ O&A_2&\ast&\cdots&\ast\\ \vdots&\ddots&\ddots&\ddots&\ast\\ O&\cdots&O&A_{s-1}&\ast\\ O&O&\cdots&O&A_s\\ \end{pmatrix} $$ ただし、\(A_i\)は既約な正方行列である。定理1.の証明は【幾何学の基礎シリーズ】グラフ理論編 その7を御覧ください。
この定理1.から、以降考える行列\(A\)は
$$
A=\begin{pmatrix}
A_1&\ast&\ast&\cdots&\ast\\
O&A_2&\ast&\cdots&\ast\\
\vdots&\ddots&\ddots&\ddots&\ast\\
O&\cdots&O&A_{s-1}&\ast\\
O&O&\cdots&O&A_s\\
\end{pmatrix}\tag{1}
$$
(ただし、\(A_i\)は既約な正方行列)としてOKです。
\(A\)の行列式について考えてみます。
ここで、行列式の性質を思い出します。
定理2.
\(X\)を\(n\)次正方行列とし、\(n=r+s\)を満たすような自然数\(r,s\)に対して、\(A\)を\(r\)次正方行列、\(B\)を\((r,s)\)型の行列、\(O\)を\((s,r)\)型の零行列、\(D\)を\(s\)次正方行列とする。このとき、 $$ |X|= \left| \begin{array}{c} A&B\\ O&D\\ \end{array} \right|=|A|\cdot|D| $$ である。定理2.の証明は【線型代数学の基礎シリーズ】行列式編 その2を御覧ください。
この定理2.を繰り返し使うことで
$$
\det\left(xI-A\right)=\det\left(xI_1-A_1 \right)\cdots\det\left( xI_s-A_s\right)
$$
となります。
ただし、\(x\)は\(A\)の固有値、\(I\)は\(n\)次の単位行列、\(I_i\)は各\(A_i\)と次数が等しい単位行列です。
従って、\(A\)の固有値は\(A_1,\dots,A_s\)の固有値をあわせたものになっています。
この事実から、定理0.(ペロン-フロベニウスの定理)の証明は\(A\)が既約な場合に帰着することが出来ます。
実際、既約な場合に定理0.が成り立つことを仮定して、\(\lambda(A_i)\)を\(A_i\)の最大の固有値とすると、
$$
\lambda(A)=\max\left\{\lambda(A_1),\dots,\lambda(A_s)\right\}
$$
とおくことで、これが\(A\)の最大の固有値となっています。
次に定理0.の主張の3.が\(A\)について成り立つことを確かめてみましょう。
注意すべきなのは、
$$
\max_{j=1,\dots,n}\sum_{i=1}^na_{ij},\quad \min_{j=1,\dots,n}\sum_{i=1}^na_{ij}
$$
は、それぞれ添字を並び替えても値は変わらないということです。
実際、\(b_{ij}=a_{\sigma(i)\ \sigma(j)}\)とすると、
$$
\max_{j=1,\dots,n}\sum_{i=1}^nb_{ij}=\max_{j=1,\dots,n}\sum_{i=1}^na_{\sigma(i)\ \sigma(j)}=\max_{j=1,\dots,n}\sum_{i=1}^na_{ij}
$$
だからです。
最小値についても同様です。
最大値に対する不等式を証明するために、\(\lambda(A)=\lambda(A_h)\)となるような\(h\)を取って、\(A_h=\left( a_{ij}^{(h)}\right)\)としましょう。
すると、
$$
\lambda(A_h)\leq \max_{j}\sum_{i}a_{ij}^{(h)}
$$
です。
ここで、\(i,j\)は\(A_h\)の添字を動きます。
$$
\max_{j}\sum_{i}a_{ij}^{(h)}\leq \max_{j=1,\dots,n}\sum_{i=1}^na_{ij}
$$
だから(メンバーを多くすれば最大値は大きくなるし、\(0\)以上の成分を持つことから和の中のメンバーを多くすれば和も大きくなります)、一般の\(A\)に対しても主張3.の最大値に関する不等式が正しいことが分かります。
次に、最小値を考えてみます。
\(\lambda(A_1)\leq\lambda(A)\)であり、\(A_1\)に対して主張が正しいとしているわけですので、\(n_1\)を\(A_1\)の次数とすると
$$
\min_{j}\sum_{i}a_{ij}^{(1)}=\min_{1\leq j\leq n_1}\sum_{i=1}^na_{ij}\geq\min_{1\leq j\leq n}\sum_{i=1}^na_{ij}
$$
となって、最小値に関する不等式も証明されました。
ペロン-フロベニウスの定理を証明するための補題集
では、いよいよ本格的に準備に入ります。
\(A\)を成分が非負な\(n\)次正方行列とし、これに付随する有向グラフを\(X\)とします。
また、\(A^k\)の\((i,j)\)成分を\(a_{ij}^{(k)}\)で表します。
補題1.
補題.
次の2条件は同値である。- \(A\)は既約である。
- 任意の\(i,j\)に対して、\(a_{ij}^{(k)}>0\)となる自然数\(k\)が存在する。
補題1.の証明
\(A\)は
$$
A=\begin{pmatrix}
A_1&\ast&\ast&\cdots&\ast\\
O&A_2&\ast&\cdots&\ast\\
\vdots&\ddots&\ddots&\ddots&\ast\\
O&\cdots&O&A_{s-1}&\ast\\
O&O&\cdots&O&A_s\\
\end{pmatrix}\tag{1}
$$
という形をしているため、
$$
a_{ij}^{(k)}=\sum_{i_1,\dots,i_{k-1}=!}^na_{ii_1}a_{i_1i_2}\cdots a_{i_{k-1}j}
$$
です。
ここで、\(A\)の成分がすべて非負ですから、
が成り立ちます。
ところが、\(a_{ii_1}a_{i_1i_2}\cdots a_{i_{k-1}j}>0\)となるのは、\(a_{ii_1},\ a_{i_1i_2},\cdots ,\ a_{i_{k-1}j}\)がすべて正のときです。
すなわち、頂点\(j\)を始点とし頂点\(i_{k-1}\)を終点、\(\cdots\)、頂点\(i_2\)を始点とし頂点\(i_1\)を終点、頂点\(i_1\)を始点とし頂点\(i\)が終点となるような有向元がそれぞれ存在することになります。
これはつまり、頂点\(j\)から頂点\(i\)への路が存在することを表しています。
故に同値です。
補題1.の証明終わり
以下、\(A\)は既約、すなわち\(A\)に付随する有向グラフ\(X\)は強連結だとします。
補題2.
補題2.
任意の\(i,j\)に対して、\(i\)を始点、\(j\)を終点とし、\(\left|c\right|\leq n-1\)であるような路\(c\)が存在する。補題2.の証明
\(A\)の既約性から有向グラフ\(X\)が強連結なので、頂点\(i\)を始点、頂点\(j\)を終点とする路\(c^\prime\)が存在します。
このとき、仮に\(\left|c^\prime\right|\geq n\)だとすると、路\(c^\prime\)上の頂点を数えると少なくとも\(n+1\)個あるから(\(X\)の頂点の数は\(n\)個)、必ずその中に同じものがなければなりません。
この頂点でショートカットすれば、\(c^\prime\)より短い路が得られます。
これをより正確に書けば、ある路\(c^\prime\)が存在して、
です。
そして\(\left|c^\prime\right|\geq n\)とすると、\(c^\prime\)が経由する頂点は始点\(i\)と終点\(j\)を含めて少なくとも\(n+1\)個存在します(各辺につき2頂点あるため、辺が\(n\)個であれば、\(n\)個の辺の両端にある頂点の個数は\(n+1\)個)。
今、\(X=(V,E)\)において\(\left|E\right|=n\)により、\(c^\prime=\left( e_1,\dots,e_n\right)\)とし、\(o(e_1)=i\)かつ\(t(e_n)=j\)とすると、\(o(c_0)=t(c_0)\)という路\(c^\prime\)の部分\(c_0=\left( e_s,\dots,e_t\right)\)が存在することになります。
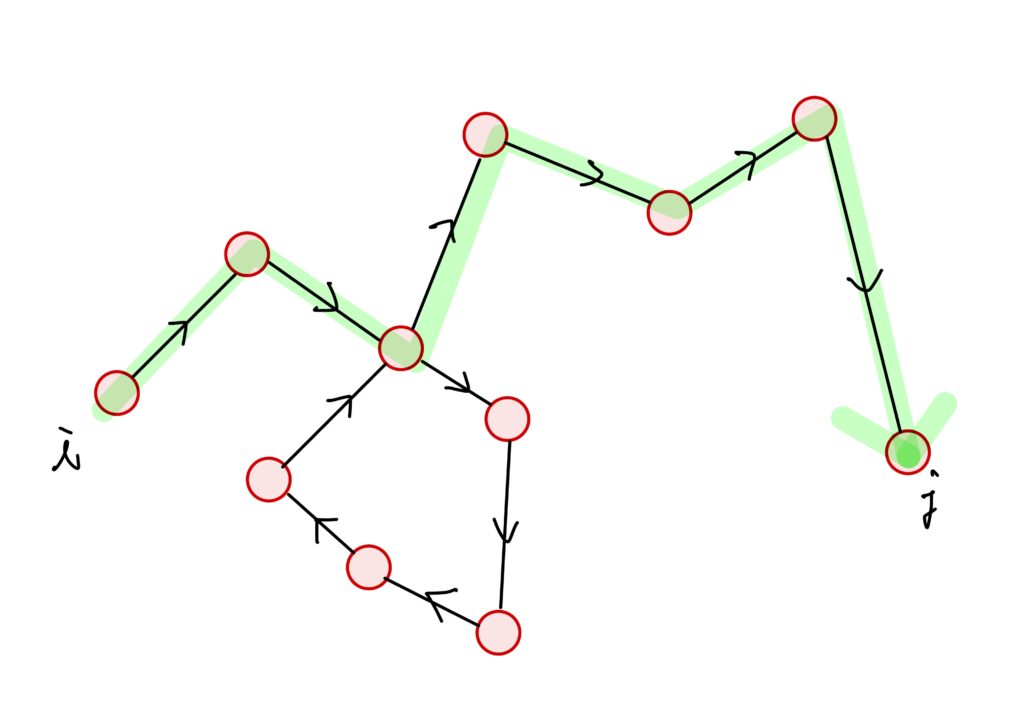
補題2.の証明終わり
余談(抽斗論法)
補題2.の証明で用いたのは抽斗論法(ひきだしろんぽう)というもので、これはディリクレの抽斗論法と呼ばれます。
抽斗論法は鳩ノ巣論法、鳩ノ巣原理とも呼ばれます。
ちなみに、ディリクレ(P. G. Dirichlet;1805-1859)は数の研究に解析学を用いたことで有名です。
補題3.
補題3.
$$\left(A+I\right)^{n-1}>0.$$補題3.の証明
補題2.により、任意の\(i,j\)に対して\(A^k\)の第\((i,j)\)成分が正になるような\(0\leq k\leq n-1\)が存在します。
また、
$$
\left(A+I \right)^{n-1}=\sum_{k=0}^{n-1}
\left(
\begin{array}{c}
n-1\\
k
\end{array}\right)
A^k
\left(=
\sum_{k=0}^{n-1}
{}_{n-1}C_k
A^k
\right)
$$
だから、\(\left(A+I \right)^{n-1}\)の第\((i,j)\)成分は正です。
補題3.の証明終わり
皆様のコメントを下さい!
今回からちょっとしたクイズを始めようと思います。
次の数学ジョークを御覧ください。
ある人「どうして数学者はいつもハロウィンとクリスマスを混同しちゃうんだい?」
数学者「…だからだよ。」
この数学者が言ったことを予想してみて下さい!
コメントでお待ちしております!
結
今回は、ペロン-フロベニウスの定理の証明のための準備をしました。
また、簡単にではありますが、ペロン-フロベニウスの定理の応用先についても述べました。
次回はペロン-フロベニウスの定理を証明します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。





コメントをする
マルコフモデルの詳細を知りたいときに確認させていただきました。読んでいた本には導出が無かったため参考になりました。ありがとうございます!!
べっこう飴様
コメントありがとうございます!
べっこう飴様の勉強の一助となれて嬉しいです!