本記事の内容
本記事は行列の既約性と強連結成分との関係を説明する記事です。
本記事を読むにあたり、強連結と強連結成分について知っている必要があるため、以下の記事も合わせてご覧ください。
↓強連結性の記事
↓強連結成分の記事
前々回、前回、今回で言いたいこと
前々回、前回、次回で言いたいことは次の2つです。
定理0-1.
与えられた\(n\)次の正方行列\(A=\left( a_{ij}\right)\)が可約であれば、添字の番号を並べ替えることにより、次の行列に変形することが出来る。 $$ \begin{pmatrix} A_1&\ast&\ast&\cdots&\ast\\ O&A_2&\ast&\cdots&\ast\\ \vdots&\ddots&\ddots&\ddots&\ast\\ O&\cdots&O&A_{s-1}&\ast\\ O&O&\cdots&O&A_s\\ \end{pmatrix} $$ ただし、\(A_i\)は既約な正方行列である。定理0-2.
有向グラフが強連結であることと、有向グラフの隣接行列が既約であることは同値である。今回は、これらを示します。
前回の軽い復習
有向グラフ\(X^o=(V,E)\)の頂点の集合\(V\)に同値関係を定める。
頂点の集合における関係
与えられた有向グラフの頂点の集合を\(V=\left\{1,\dots,n\right\}\)とし、任意の頂点\(i,j\in V\)に対して次の関係を定める。この関係\(\sim\)は同値関係でした。
\(\sim\)が同値関係であることの証明は【幾何学の基礎シリーズ】グラフ理論編 その6を御覧ください。
\(V\)の分割
先程定めた関係\(\sim\)は同値関係ですので、\(V\)を次のように分割することが出来ます。
$$
V=V_1\cup V_2\cup\cdots\cup V_s
$$
だたし、各\(V_a\)は、その中の2頂点\(i,j\)に対して\(i\sim j\)が成り立ち、しかもこの性質を持つ最大のものです。
要するに、各\(V_a\)は関係\(\sim\)による同値類です。
各\(V_a\)は同値類ですから、任意の\(1\leq p,q\leq s\)を満たす自然数\(p,q\)に対して、\(V_p\cap V_q=\emptyset\)であることに注意です。
強連結成分
各\(V_a\)に対して、\(V_a\)の2頂点を結ぶ路上にある辺を全て集めて、\(V_a\)を頂点の集まりとする有向グラフを作ります。
このグラフを\(X_\alpha^o\)で表すことにしましょう。
たとえは次のようなグラフです。
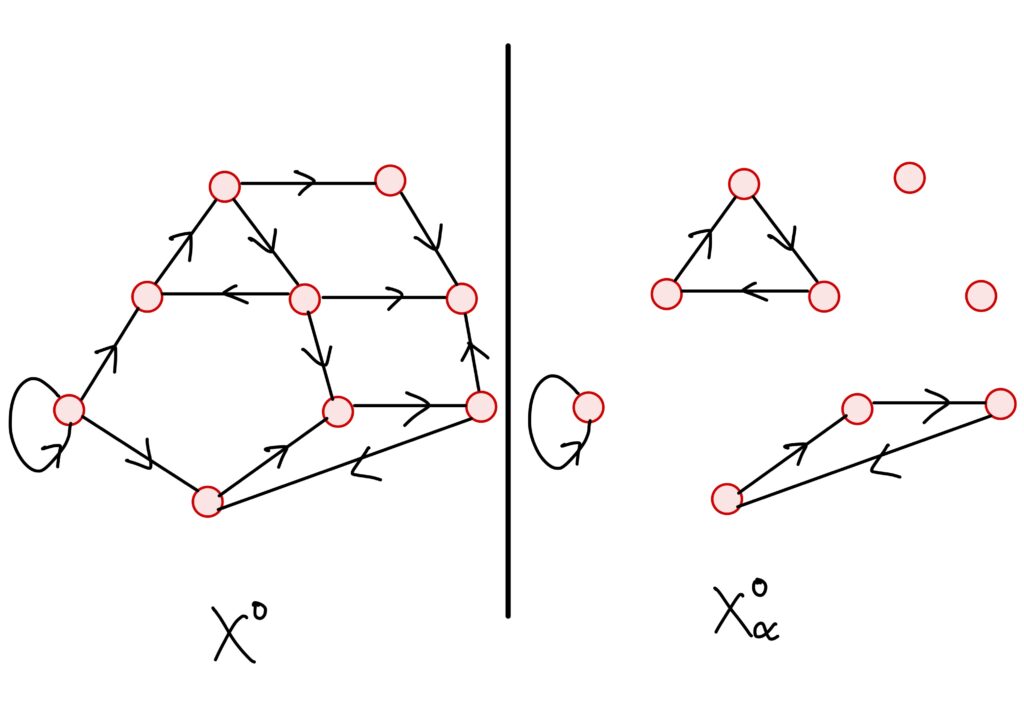
すなわち、以下でした。
強連結成分
有向グラフ\(X^o\)の強連結な部分グラフ\(X_1^o\)を\(X^o\)の強連結成分という。\(V_1,\dots,V_s\)の順序
\(V_1,\dots,V_s\)の順序
この関係\(\leq\)は以下を満たしていたのでした。
- \(V_a\leq V_a\)
- \(V_a\leq V_b,\ V_b\leq V_a\ \Rightarrow\ V_a=V_b\)
- \(V_a\leq V_b,\ V_b\leq V_c\ \Rightarrow\ V_a\leq V_c\)
この証明は【幾何学の基礎シリーズ】グラフ理論編 その6を御覧ください。
\(V_a\)たちの番号付けと\(V_a\)の中の頂点の番号付け
\(V_a\)たちの番号付け
\(V_a\)たちに次の規則で番号を付けます。
- \(V_b<V_a\)となる\(V_b\)が存在しないような\(V_a\)を選び(複数あるかもしれません)、これを極小元といい、これに番号\(1\)を付ける。
複数ある場合は一方を任意に選び番号\(1\)を付ける。 - \(V_a\)を取り除いたものの中で、極小元を選び、それに番号\(2\)を付ける。
- この操作を繰り返す。
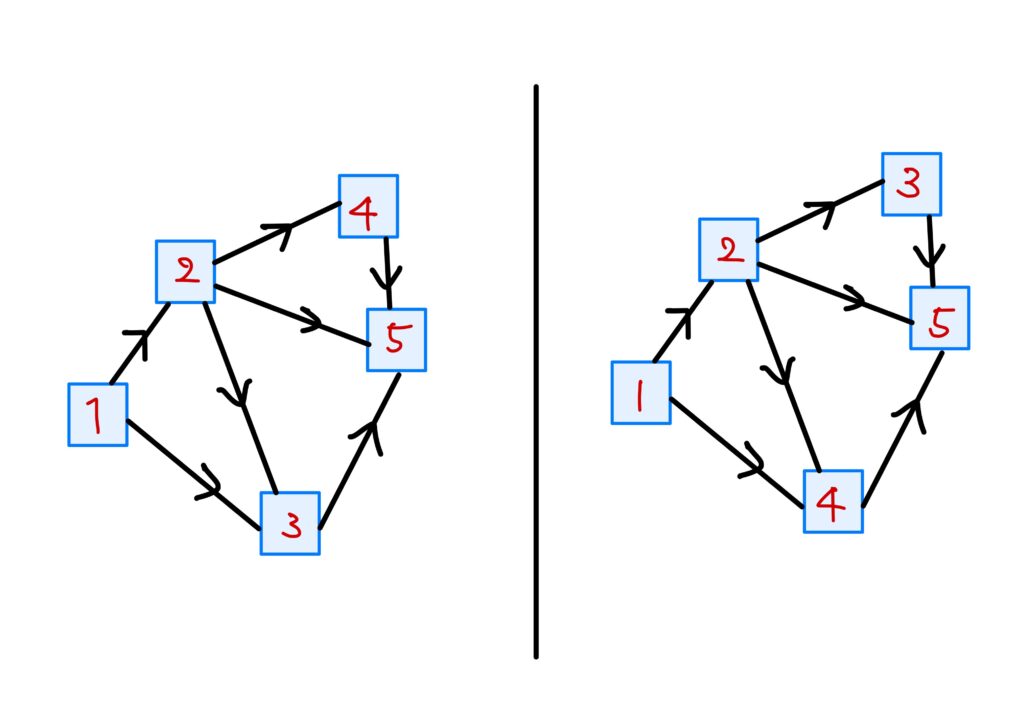
この番号付けと、先程定めた\(\left\{V_a\right\}\)の順序関係\(\leq\)は次のように関連しています。
数の大小関係として\(i\leq j\)が成り立つ(逆は一般に成り立たない)。
そこで、\(V_a\)の番号が\(i\)であるときに、改めて\(V_a\)を\(V_i\)と書くことにしましょう。
先程述べた通り、数として\(i<j\)であるとき、\(V_j\)から\(V_i\)への路は存在しません。
\(V_a\)の中の頂点の番号付け
各\(V_i\)の頂点の数を\(n_i\)として表し、\(V_i\)の頂点にも次の規則で番号付けします。
- \(V_1\)の頂点には、\(1,2,\dots,n_1\)の番号
- \(V_2\)の頂点には、\(n_1+1,n_1+2,\dots,n_1+n_2\)の番号
\(\vdots\) - 以下同様にして、\(V_s\)の頂点には\(n_1+\cdots+n_{s-1}+1,\ n_1+\cdots+n_{s-1}+2,\dots ,\ n_1+\cdots+n_{s-1}+n_s=n\)の番号
を付けます。
こうして、元々の有向グラフ\(X^o\)の頂点に新しい番号が付けられました。
そこで、新しい番号\(k\)を持つ頂点の要素の番号が\(i_k\)だったとして、置換\(\sigma\)を
$$
\sigma=
\left(\begin{array}{c}
1&2&\cdots&n\\
i_1&i_2&\cdots&i_n\\
\end{array}\right)
$$
で定めます。
詳しくは…
詳しくは
を御覧ください。
定理0-1.の証明
いよいよ、定理0-1.の証明に入っていきます。
定理0-1.の証明
今から、\(X^o\)は行列\(A=\left( a_{ij}\right)\)に付随する有向グラフとします。
新しい番号で\(i\)から\(j\)に向かう有向編があれば、それは元の番号で\(\sigma(i)\)から\(\sigma(j)\)に向かう有向辺だから、\(a_{\sigma(i)\ \sigma(j)}\neq0\)であり、かつ逆も成り立ちます。
また、番号の付け方から次が成り立ちます。
- \(i\in V_\alpha\)、\(j\in V_\beta\)で\(\beta<\alpha\)であれば、\(a_{\sigma(i)\ \sigma(j)}=0\)です。
- \(n_\alpha\)次の正方行列\(A_\alpha=\left( a_{\sigma(i)\ \sigma(j)}\right)\ (i,j\in V_\alpha)\)に対する有向グラフは\(X^o_\alpha\)であり、従って強連結です。
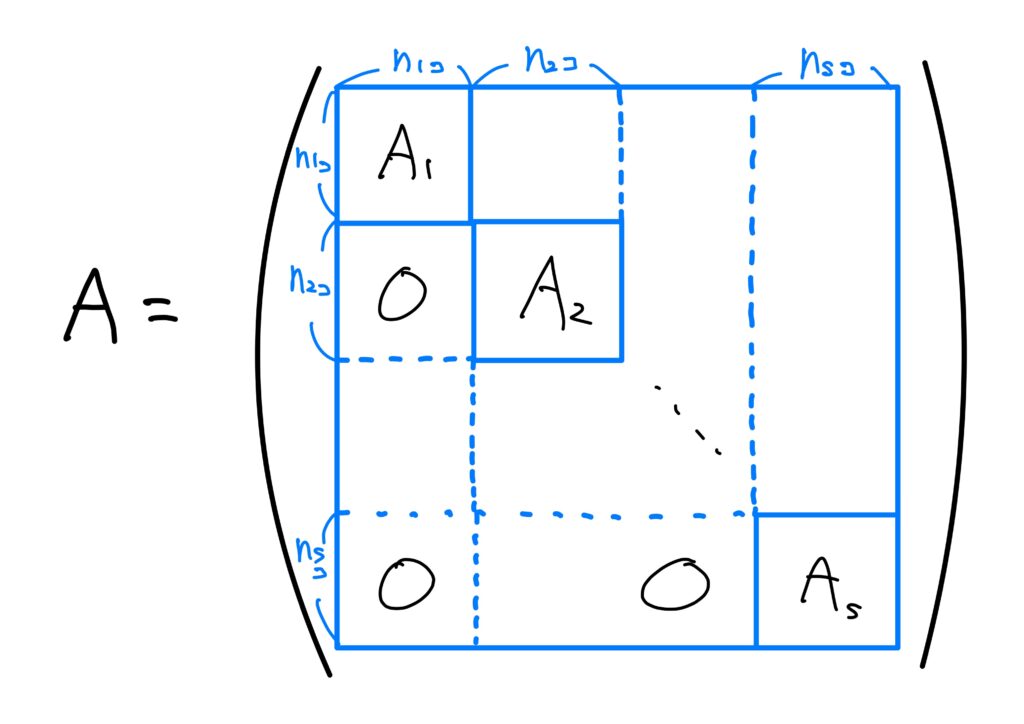
こうして番号の付け替えにより行列\(A\)は
$$
\begin{pmatrix}
A_1&\ast&\ast&\cdots&\ast\\
O&A_2&\ast&\cdots&\ast\\
\vdots&\ddots&\ddots&\ddots&\ast\\
O&\cdots&O&A_{s-1}&\ast\\
O&O&\cdots&O&A_s\\
\end{pmatrix}
$$
に変形されます。
定理0-1.の証明終わり
故に、前々回証明した
定理5.
可約な\(n\)次正方行列\(A\)に対する有向グラフ\(X^o\)は強連結ではない。対偶を取れば、有向グラフ\(X^o\)が強連結であれば、\(X^o\)の隣接行列\(A\)は既約である。から
定理0-2.
有向グラフが強連結であることと、有向グラフの隣接行列が既約であることは同値である。が成り立つわけです。
皆様のコメントを下さい!
数学者ジョークをシリーズ化しようかなあと思っています。
今回も今回とてジョークを紹介します。
Aさん「\(\displaystyle\frac{1}{\rm cabin}\)の積分は?」
Bさん「天然の丸太(natural log→自然対数)で出来た小屋(cabin)」※\(\displaystyle\int\frac{1}{\rm cabin}\ d{\rm cabin}=\log\left|{\rm cabin}\right|\)の意。
Aさん「不正解。答えはハウスボードだ。君は\(C\)(→sea→海)を加えるのを忘れている。」
こんな会話を日常的にしていたら気持ち悪がられますよね。
皆様がご存知のジョークをコメントで教えて下さい!
結
今回は、「有向グラフが強連結であることと、有向グラフの隣接行列が既約であることは同値である。」という主張の証明を完結させました。
有向グラフの強連結性を知るには隣接行列の既約性に注目すれば良い、ということです。
逆に、既約な正方行列が与えられたらば、それから強連結なグラフを作ることが出来ます。
次回はペロン-フロベニウスの定理の紹介とその準備をします。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
この記事の内容をより詳しく知りたい方は以下の書籍を御覧ください!





コメントをする