本記事の内容
本記事はペロン-フロベニウスの定理の証明をする記事です。
本記事を読むにあたり、いくつか補題を知っている必要があるため、以下の記事も合わせてご覧ください。
ペロン-フロベニウスの定理の主張の復習
ペロン-フロベニウスの定理は以下でした。
定理0.(Perron-Frobeniusの定理)
成分がすべて非負な既約\(n\)次正方行列\(A=\left(a_{ij} \right)\)は\(A\neq O\)であるとき、次の性質を満たす固有値\(\lambda(A)\)を持つ。- \(\lambda(A)>0\)であり、\(\lambda(A)\)は特性根として単根である。さらに成分が正の固有ベクトルを持つ。
- \(A\)の任意の固有値\(\lambda\)について、\(\left|\lambda\right|\leq \lambda(A)\)が成り立つ。すなわち\(\lambda(A)\)は\(A\)の最大な正の固有値である。
- \(A\boldsymbol{x}=\lambda\boldsymbol{x}\)、\(\boldsymbol{x}\geq0\)、\(\boldsymbol{x}\neq\boldsymbol{0}\)であるとき、\(\lambda=\lambda(A)\)かつ\(\boldsymbol{x}>0\)が成り立つ。
- \(\displaystyle\min_{j=1,\dots,n}\sum_{i=1}^na_{ij}\leq\lambda(A)\leq\max_{j=1,\dots,n}\sum_{i=1}^na_{ij}\)、\(\displaystyle\min_{i=1,\dots,n}\sum_{j=1}^na_{ij}\leq\lambda(A)\leq\max_{i=1,\dots,n}\sum_{j=1}^na_{ij}\)
今回はこの定理を証明します。
証明の前に…(上下半連続)
上(下)半連続について少し述べます。
上(下)半連続というのは、一言で述べると
です。
これを厳密に書くと、
上(下)半連続
- 上半連続 関数\(f:\mathbb{R}\supset X\to\mathbb{R}\)が与えられたとき、\(c\in\mathbb{R}\)を選べば、\(f\)が定める値が\(c\)以上になるような定義域\(X\)上の点\(x\)からなる集合を $$ U(c)=\left\{x\in X\middle|f(x)\geq c\right\} $$ と定める。これを関数\(f\)の\(c\)に関する上方位集合(uppercontour set)という。
- 下半連続 関数\(f:\mathbb{R}\supset X\to\mathbb{R}\)が与えられたとき、\(c\in\mathbb{R}\)を選べば、\(f\)が定める値が\(c\)以下になるような定義域\(X\)上の点\(x\)からなる集合を $$ L(c)=\left\{x\in X\middle|f(x)\leq c\right\} $$ と定める。これを関数\(f\)の\(c\)に関する下方位集合(lowercontour set)という。
任意の\(c\in\mathbb{R}\)に対する上方位集合\(U(c)\)が\(X\)上の閉集合である場合、\(f\)は上半連続(upper semi-continuous)であるという。
任意の\(c\in\mathbb{R}\)に対する下方位集合\(L(c)\)が\(X\)上の閉集合である場合、\(f\)は下半連続(lower semi-continuous)であるという。
例1. \(\displaystyle f(x)=\begin{cases}x^2&x\neq0\\1&x=0\end{cases}\)とします。
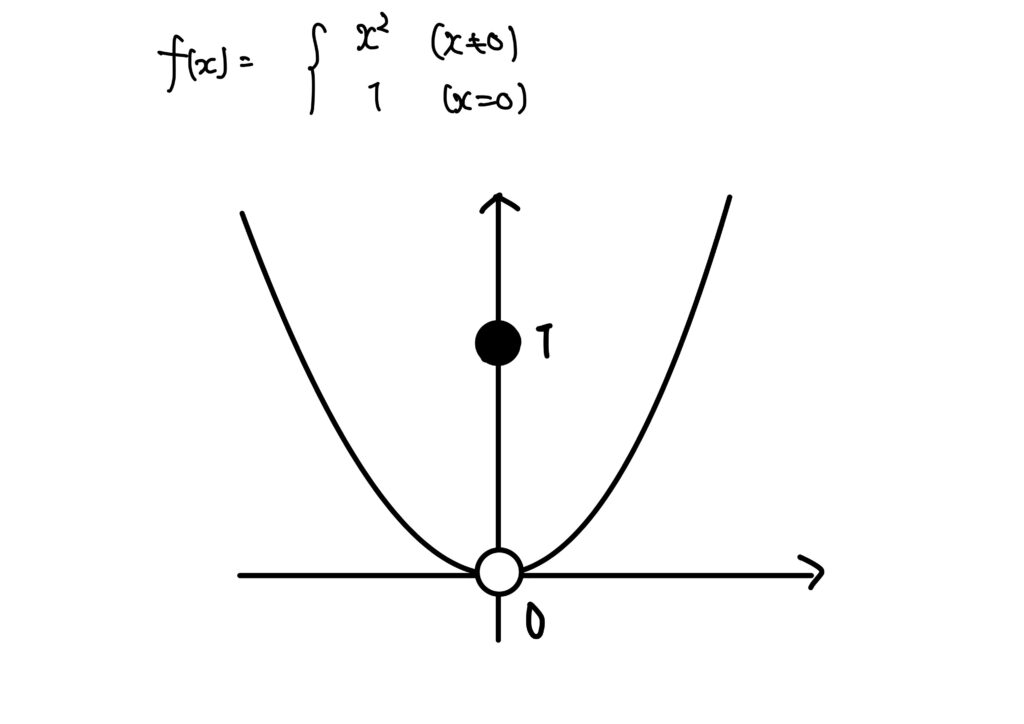
この関数\(f\)は上半連続です。
実際、\(c\leq0\)を満たす\(c\in\mathbb{R}\)を任意に選んだとき、上方位集合は
\begin{eqnarray}
U(c)&=&\left\{x\in\mathbb{R}\middle|f(x)\geq c\right\}\\
&=&\mathbb{R}
\end{eqnarray}
となりますが、\(\mathbb{R}\)すなわち\(U(c)\)は\(\mathbb{R}\)上の閉集合です。
次に\(0<c\leq1\)の場合を考えてみます。
このときの上方位集合は
\begin{eqnarray}
U(c)&=&\left\{x\in\mathbb{R}\middle|f(x)\geq c\right\}\\
&=&(-\infty,-\sqrt{c}]\cup\{0\}\cup[\sqrt{c},+\infty)
\end{eqnarray}
となりますが、\(\mathbb{R}\)上の1点のみから成る集合と、\((-\infty,-\sqrt{c}]\)と\([\sqrt{c},+\infty)\)は閉集合であり、そして有限個の閉集合の和集合もまた閉集合ですので、\(U(c)\)は閉集合です。
最後に\(c>1\)の場合を考えてみます。
このときの上方位集合は
\begin{eqnarray}
U(c)&=&\left\{x\in\mathbb{R}\middle|f(x)\geq c\right\}\\
&=&(-\infty,-\sqrt{c}]\cup[\sqrt{c},+\infty)
\end{eqnarray}
となりますが、先と同様に\(U(c)\)は閉集合です。
以上のことから\(f\)は上半連続です。
例2. \(\displaystyle f(x)=\begin{cases}x^2&x\neq0\\-1&x=0\end{cases}\)とします。
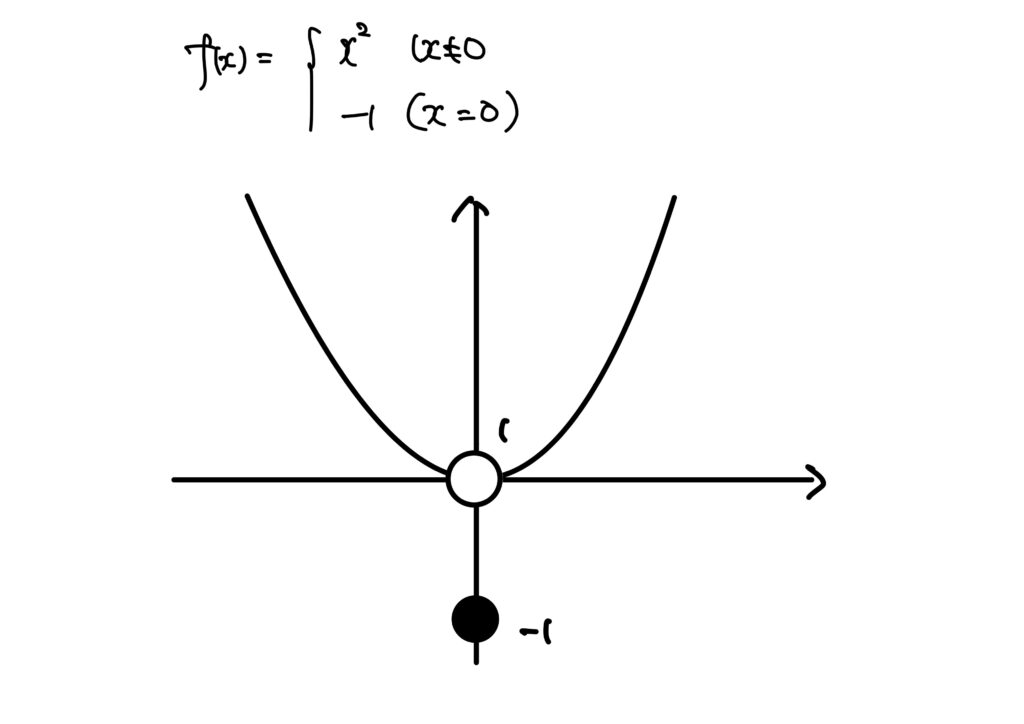
この関数\(f\)は上半連続ではありません。
実際、\(-1<c\leq 0\)を満たす\(c\in\mathbb{R}\)に注目したとき、
\begin{eqnarray}
U(c)&=&\left\{x\in\mathbb{R}\middle|f(x)\geq c\right\}\\
&=&(-\infty,0)\cup(0,+\infty)
\end{eqnarray}
となりますが、\((-\infty,0)\)と\((0,+\infty)\)はともに開集合であり、開集合の和集合もまた開集合なので、\(U(c)\)は開集合です。
故に閉集合ではありません。
従って、\(f\)は上半連続ではありません。
上半連続であるような関数の性質として次があります。
定理3.
関数\(f:X\to\mathbb{R}\)が上半連続であれば、\(f\)は\(X\)で最大値を持つ。この定理3.の証明は後の位相空間論の記事で証明しようと思いますのでそれまでお待ちを…
ペロンフロベニウスの定理の証明
いくつかステップに分けて証明します。
\(\boldsymbol{x}\geq0\)と書いたらば、ベクトル\(\boldsymbol{x}\)の成分がすべて\(0\)以上である、ということを表しています。
ペロン-フロベニウスの定理の証明
ステップ1
\(\boldsymbol{x}\geq0\)、\(\boldsymbol{x}\neq\boldsymbol{0}\)に対して、
$$
\alpha(\boldsymbol{x})=\max\left\{\rho\middle|A\boldsymbol{x}\geq\rho\boldsymbol{x}\right\}
$$
とします。
ただし、一般にベクトル\(\boldsymbol{x}\)、\(\boldsymbol{y}\)に対して\(\boldsymbol{x}\geq\boldsymbol{y}\)は\(\boldsymbol{x}-\boldsymbol{y}\geq0\)の意味です。
このとき、次の2つが成り立ちます。
- \(\alpha(\boldsymbol{x})\)は\(\boldsymbol{x}\)に関して領域\(D=\left\{\boldsymbol{x}\middle|\boldsymbol{x}\geq0,\ \boldsymbol{x}\neq\boldsymbol{0}\right\}\)上で連続である。
- \(\alpha(\boldsymbol{x}_0)=\left\{\alpha(\boldsymbol{x})\middle|\boldsymbol{x}\geq0,\ \boldsymbol{x}\neq\boldsymbol{0}\right\}\)を満たす\(\boldsymbol{x}_0\geq0\ (\boldsymbol{x}\neq\boldsymbol{0})\)が存在する。
これを示すために\(K=\left\{\boldsymbol{x}\geq0\middle|\left|\boldsymbol{x}\right|=1\right\}\)とします。
ただし、\(\boldsymbol{x}=\left(x_1,\dots,x_n \right)\)に対して
$$
\left|\boldsymbol{x}\right|=\max\left\{\left|x_1\right|,\dots,\left|x_n\right|\right\}
$$
とします。
さらに、\(T=\left( A+I\right)^{N-1}\ \)(ただし、\(I\)は単位行列)とすると\(T\)は連続です。
実際、\(T(\boldsymbol{x})=\left( A+I\right)^{N-1}(\boldsymbol{x})\)は多項式関数だからです。
\(K\)は有界な閉集合であり(四分円だから)、関数\(T\)は連続なので、有界閉集合上の連続関数の像は有界閉集合だから、\(T(K)\)も有界閉集合です。
ここで、次の事実を使います。
補題3.
$$\left(A+I\right)^{n-1}>0.$$補題3.の証明は【幾何学の基礎シリーズ】グラフ理論編 その8を御覧ください。
補題3.により、\(\boldsymbol{y}\in T(K)\)は成分がすべて正のベクトルです。
\(\alpha(\boldsymbol{y})\)は上半連続なので、定理3.から\(\alpha(\boldsymbol{x}_0)=\max\left\{\alpha(\boldsymbol{y})\middle|\boldsymbol{y}\in T(K)\right\}\)を満たす\(\boldsymbol{x}_0\in T(K)\)が存在します。
これが求めたいものであることを見てみましょう。
\(\boldsymbol{x}\geq0\)かつ\(\boldsymbol{x}\neq\boldsymbol{0}\)であるような\(\boldsymbol{x}\)に対して、\(\hat{\boldsymbol{x}}=\boldsymbol{x}\left|\boldsymbol{x}\right|^{-1}\in K\)と置きます。
このとき、\(\alpha(\boldsymbol{x})=\alpha(\hat{\boldsymbol{x}})\)が成り立つので、
$$
A\hat{\boldsymbol{x}}\geq\alpha(\boldsymbol{x})\hat{\boldsymbol{x}}
$$
及び
$$
TA\hat{\boldsymbol{x}}\geq\alpha(\boldsymbol{x})T\hat{\boldsymbol{x}}
$$
が成り立ちます。
\(TA=AT\)だから、
$$
AT\hat{\boldsymbol{x}}\geq\alpha(\boldsymbol{x})T\hat{\boldsymbol{x}}
$$
を得るので、\(\alpha\left(T\hat{\boldsymbol{x}} \right)\geq\alpha(\boldsymbol{x})\)となります。
\(T\hat{\boldsymbol{x}}\in T(K)\)だから
$$
\alpha(\boldsymbol{x}_0)\geq\alpha\left(T\hat{\boldsymbol{x}} \right)\geq\alpha(\boldsymbol{x})
$$
となります。
ステップ2
$$
\alpha=\max\left\{\alpha(\boldsymbol{x})\middle|\boldsymbol{x}\geq0,\ \boldsymbol{x}\neq\boldsymbol{0}\right\}
$$
とすると、\(\alpha>0\)です。
このとき、以下が成り立ちます。
これを示すために\(\boldsymbol{y}=\left(A-\alpha I \right)\boldsymbol{x}\)と書きます。
\(A\boldsymbol{x}\geq\alpha(\boldsymbol{x})\boldsymbol{x}=\alpha\boldsymbol{x}\)だから、\(\boldsymbol{y}\geq0\)です。
また、\(\boldsymbol{y}\neq\boldsymbol{0}\)により、\(T\boldsymbol{y}>0\)です。
故に
$$
AT\boldsymbol{x}-\alpha T\boldsymbol{x}=\left( TA-\alpha T\right)\boldsymbol{x}=T\boldsymbol{y}>0
$$
だから、\(AT\boldsymbol{x}>\alpha\boldsymbol{x}\)です。
これはまさに\(\alpha\left( T\boldsymbol{x}\right)>\alpha\)であることを意味しているため、矛盾です。
従って、\(\boldsymbol{y}=\boldsymbol{0}\)、すなわち\(A\boldsymbol{x}=\alpha\boldsymbol{x}\)です。
ステップ3
実際、\(A\boldsymbol{y}=\lambda\boldsymbol{y}\)かつ\(\boldsymbol{y}\neq\boldsymbol{0}\)とすると、\(\boldsymbol{z}=\left( \left|y_1\right|,\dots,\left|y_n\right|\right)\)とおけば\(A\boldsymbol{z}\geq\left|\lambda\right|\boldsymbol{z}\)です。
従って、\(\alpha\geq\alpha(\boldsymbol{z})\geq\left|\lambda\right|\)です。
ステップ4
ステップ3で見たように、もし\(A\boldsymbol{y}=\lambda\boldsymbol{y}\)かつ\(\boldsymbol{y}\neq\boldsymbol{0}\)とすると、\(\alpha(\boldsymbol{z})=\alpha\)、\(\boldsymbol{z}>0\)および\(A\boldsymbol{z}=\alpha\boldsymbol{z}\)となります。
特に、\(\alpha\)に対する固有ベクトルの成分はすべて\(0\)ではありません。
\(\alpha\)に対する線型独立な2つの固有ベクトル\(\boldsymbol{y}_1\)、\(\boldsymbol{y}_2\)が存在したとすると、それらの適当な線型結合を取れば、少なくとも1つの成分を\(0\)とする事ができるため、矛盾です。
ステップ5
これを示すために、転置行列\(A^\top\)を考えます。
\(A^\top\)に対応する有向グラフはすべての有効辺の向きを逆にしたものです。
\(A^\top\)の固有値は、\(A\)の固有値と一致するから、\(\alpha\)は\(A^\top\)の固有値でもあるため、\(A^\top\boldsymbol{y}=\alpha\boldsymbol{y}\)を満たす正のベクトル\(\boldsymbol{y}\)が存在します。
故に
$$
(\lambda\boldsymbol{x},\boldsymbol{y})=\left(A\boldsymbol{x},\boldsymbol{y}\right)=\left(\boldsymbol{x}, A^\top\boldsymbol{y}\right)=\alpha(\boldsymbol{x}\cdot\boldsymbol{y})
$$
および\((\boldsymbol{x},\boldsymbol{y})\)により、\(\alpha=\lambda\)です。
ステップ6
これを示すために、
$$
m=\min_i\frac{y_i}{x_i},\quad M=\max_i\frac{y_i}{x_i}
$$
としましょう。
このとき\(mx_i\leq y_i\leq Mx_i\)です。
\(A^\top\boldsymbol{y}_0=\alpha\boldsymbol{y}_0\)を満たす\(\boldsymbol{y}_0\)を取れば、
$$
(m\boldsymbol{x}_0,\boldsymbol{y}_0)\leq(\boldsymbol{y}_0,\boldsymbol{y}_0)\leq \left(M\boldsymbol{x},\boldsymbol{y}_0 \right)
$$
です。
一方で、
$$
(\boldsymbol{y},\boldsymbol{y}_0)=\left( A\boldsymbol{x},\boldsymbol{y}_0\right)=\left( \boldsymbol{x},A^\top\boldsymbol{y}_0\right)=(\alpha\boldsymbol{x},\boldsymbol{y}_0)
$$
だから
$$
(m\boldsymbol{x},\boldsymbol{y}_0)\leq(\alpha\boldsymbol{x},\boldsymbol{y}_0)\leq \left(M\boldsymbol{x},\boldsymbol{y}_0\right)
$$
です。
従って\(m\leq\alpha\leq M\)です。
ペロン-フロベニウスの定理の証明終わり
皆様のコメントを下さい!
前回の記事で紹介したジョーク
ある人「どうして数学者はいつもハロウィンとクリスマスを混同しちゃうんだい?」
数学者「…だからだよ。」
の答えは
数学者「8進数(Oct)の31は10進数(Dec)の25だからだよ。」
でした。
なるほど。面白いですね!
次はこれです。
ある人「もし死人(DEAD people)のみが16進数を理解できるなら、16進数を理解できるのは何人でしょうか?」
数学者「…人だね。」
この数学者が言ったことを予想してみて下さい!
コメントでお待ちしております!
結
今回は、ペロン-フロベニウスの定理を証明しました。
応用先がたくさんあるこの定理ですが、グラフ理論では隣接行列を観察する際に大いに役立ちます。
次回はハミンググラフとハミング距離について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。




コメントをする