本記事の内容
本記事はグラフ理論におけるグラフとは何かを解説する記事です。
本記事を読むにあたり、集合、写像の基礎について知っている必要があるため、以下の記事も合わせてご覧ください。
※シリーズ化しているため、一部のリンクを掲載しています。
↓集合の記事
↓写像の記事
いきなりですが、クイズです。
唐突ですが、クイズを出題します。
クイズ(是非一度解いてみて下さい!)
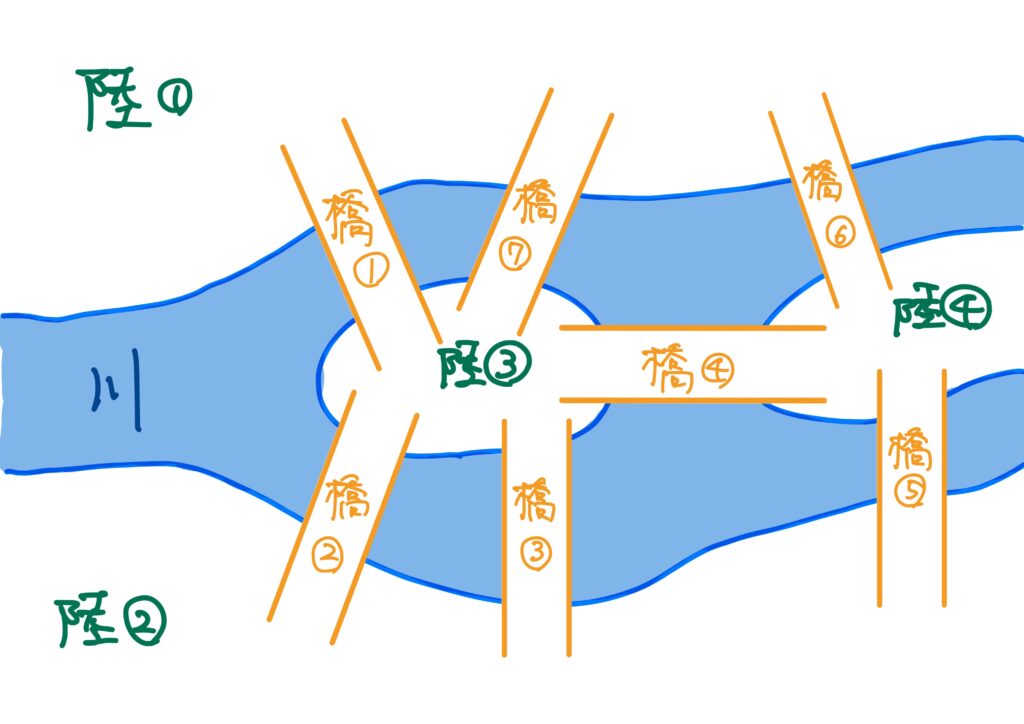
18世紀の初頭、プロイセン王国の東部の東プロイセンの首都であるケーニヒスベルク(現:ロシア連邦カリーニングラード)という大きな街がありました。この街の中心部には、プレーゲル川という大きな川が流れており、7つの橋が架かっていました(以下の図を参照)。
あるとき、街の人が次のように言いました。
「この問題が数学と関係あるの?」と思われるかもしれませんが、関係あります。
5分くらい考えてみて下さい。
考えましたか?
どうでしょう?
街の人が言ったことは実現可能でしょうか?
答えは、「不可能」です。
どうやって解決したんですか?
筆者がはじめてこの問題に出会ったのは実は高校生の時でした。
とはいえ、その後すぐに忘れてしまい、大学入学後に再度触れ、思い出したというなんとも情けないお話です。
さて、高校生の時の筆者は「出来るでしょ。ルートを見つけてやろうじゃないか。」と意気込んで愚直に色々試してみましたが、ある程度試したところで「これ、出来ないんじゃないか?」と思い諦めて答えをみました。
勿論、当時の筆者のように愚直に全パターン試せば、不可能であるということが証明できます。
しかし、面倒ですよね。
実は、1736年にレオンハルト・オイラーが以下のように問題を”置き換えて”解きました。
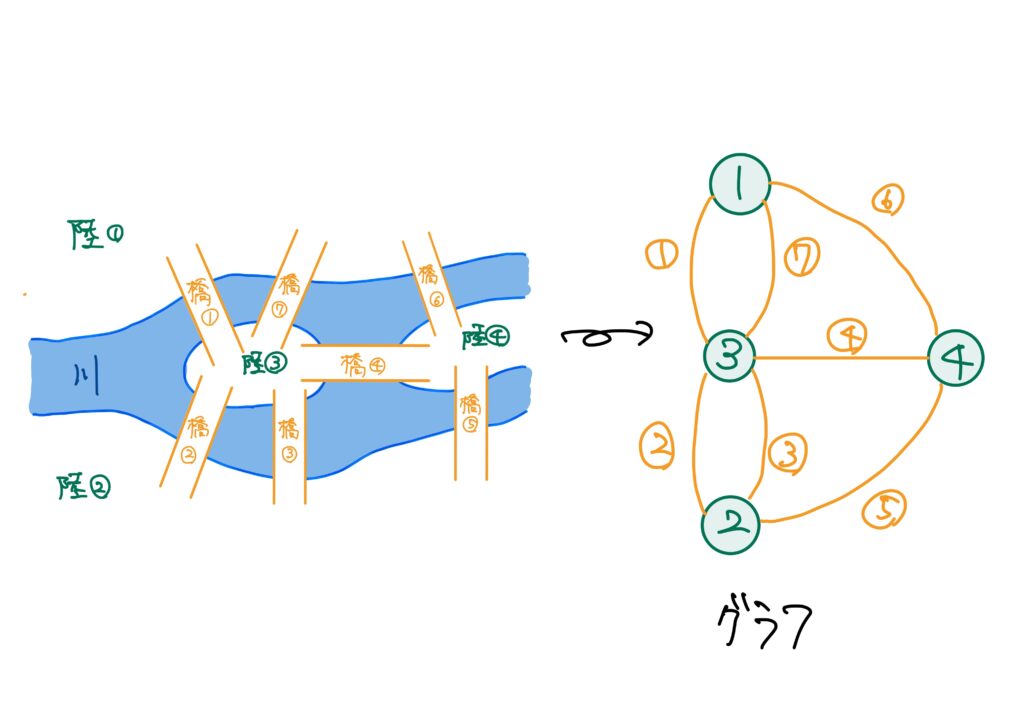
上の右側の図が本シリーズにおけるグラフと呼ばれるものです(これについては後述します)。
オイラーが上記の右図でどうやって解決したかというお話の前に「どうしてケーニヒスベルクの街の立地が右側の図になるの?」ということからお話しましょう。
どうやって作図したんですか?
シンプルです。

各陸地はの間には川が流れており、各陸地は橋でもって繋がっています。
要するに「各陸地同士が橋でどのように繋がっているか」という情報さえあれば十分であり、橋の長さやら陸の広さやらは今回の問題では関係ありません。
この発想から、各陸地を点、橋を辺で表して、どの陸地が橋でどのように繋がっているかを、点を辺でつなげることで表現した、ということです。
オイラーの解法
では、オイラーの解法を解説します(解説というより紹介ですが…)。

オイラーは上図のようにケーニヒスベルクの街をグラフ(点と線で表した図)で表現することで、問題を
という問題に置き換えました。
このグラフが一筆書き可能なのであれば、ケーニヒスベルクの橋を全て1度ずつ通って戻ってくるルートが存在することになります。
そして、オイラーは、このグラフが一筆書きできないことを証明することで、ケーニヒスベルクの橋の問題を否定的に解決しました。
一筆書きが可能かどうかの判定法
では、一筆書きできるかどうかの判定法について紹介します。
結論は以下です。
定理0.(一筆書きが可能かどうかの判定法)
与えられた連結なグラフが一筆書き可能であることの必要十分条件は以下の条件のいずれか一方が成り立つことである。- 全ての頂点の次数が偶数である。
- 2つの頂点の次数が奇数で、その他の全ての頂点の次数が偶数である。
この定理の証明はここでは行いません。
後の記事でするかもしれません。
この定理の主張を理解するにはグラフについての説明が必要ですが、言葉の意味を直感的に説明します。
まず、グラフの点のことを頂点といいます。
次に、1つの頂点に繋がっている辺の数のことを次数といいます。
最後に、どの頂点からどの頂点へも辺をたどって移動できるときに、そのグラフは連結であるといいます。
判定法を使ってケーニヒスベルクの橋の問題を解いてみます。
ケーニヒスベルクの橋の問題を先の定理0.を使って解いてみます。
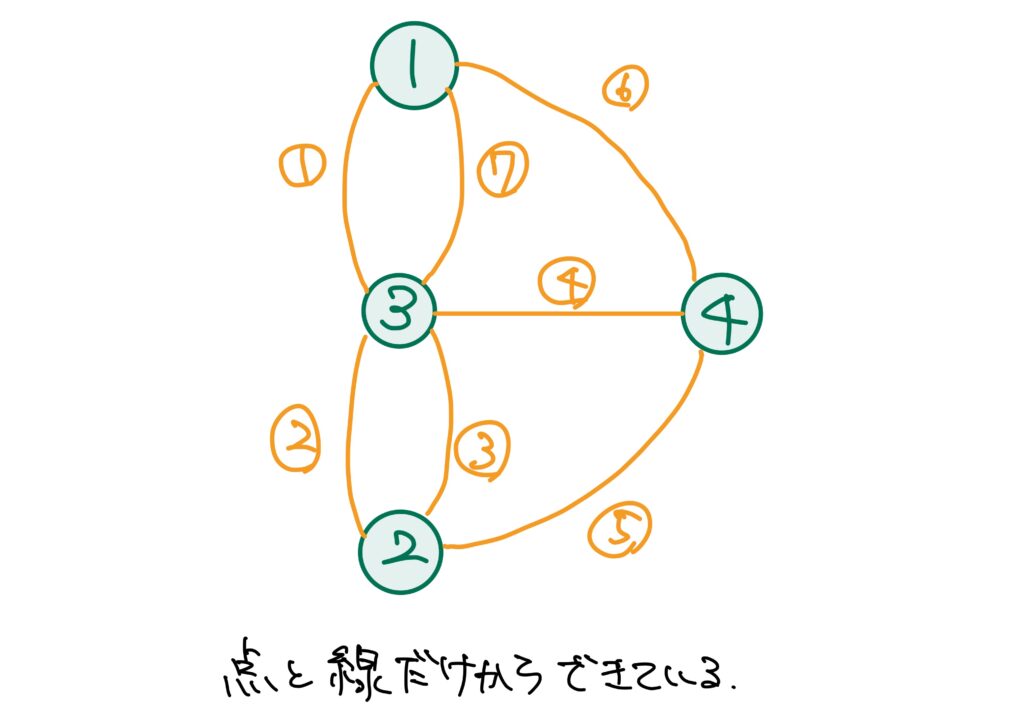
このグラフを見てみると、4つの頂点の次数が全て奇数です。
従って、定理0.によりこのグラフは一筆書きできません。
故に、ケーニヒスベルクの街は、橋を1度ずつ渡り、全ての陸地を通って元の位置に戻ることは不可能です。
数学的なグラフの話
では、今までのクイズの話から数学の話にはいっていきます。
「グラフ」という言葉について
「グラフとは何か?」ということを数学的に説明する前に、まずは「グラフ」という言葉について注意をしておきます。
“グラフ”と言われたらば、真っ先に思い浮かぶのは
ではないでしょうか。
勿論、これもグラフと呼んで差し支えありません。
しかし、本シリーズにおいてはグラフは関数のグラフのように\(x\)軸と\(y\)軸があって…というものではありません。
本シリーズで扱うグラフは”グラフ”という言葉から真っ先に想像するような関数のグラフではない、ということを注意しておきます。
グラフって何ですか?(直感的な話)
“グラフ”というのは直感的にはなんてことありません。
誠にシンプルです。
一言でいうと、
です。
たったこれだけです。
「点と線からなるモノ」のことをグラフと呼ぶわけですので、点と点との物理的な距離(ユークリッド距離)は考えません。
つまりグラフ理論とは
と言い換える事ができます。
グラフは「点と線からなるモノ」ですので、意味が誠に広いです。
故にありとあらゆるところにグラフは存在します。
これについては後述します(グラフ理論の応用例)。
先程のケーニヒスベルクの橋の問題の部分でも紹介した以下の図はまさしく点と線からなるものですのでグラフです。
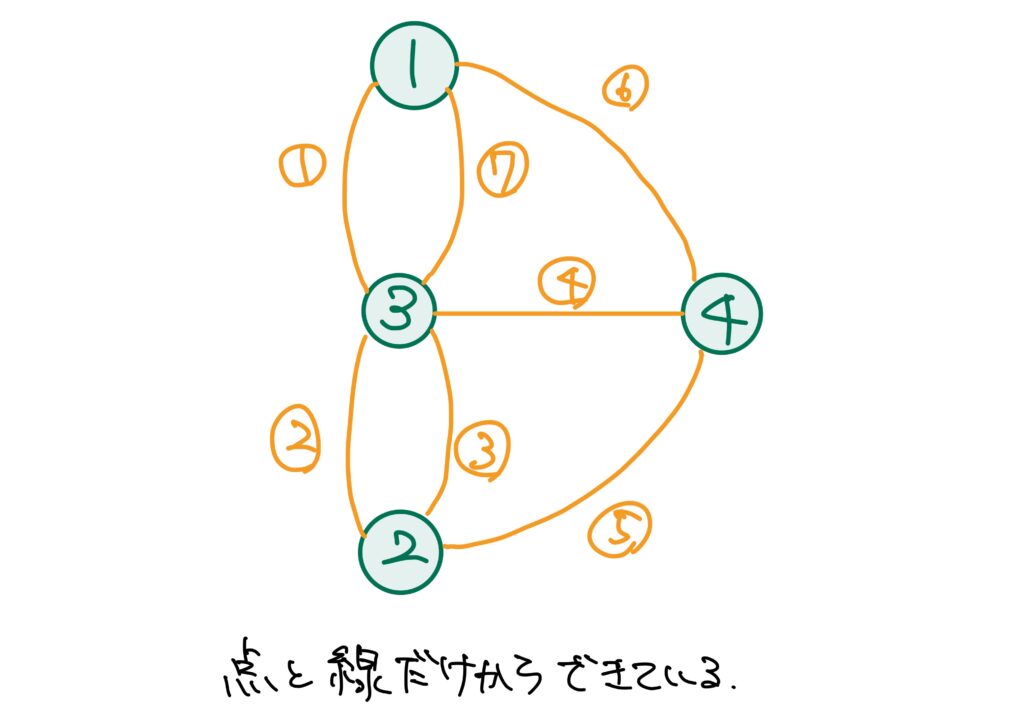
点と線からなっていればよいので、以下もグラフです。
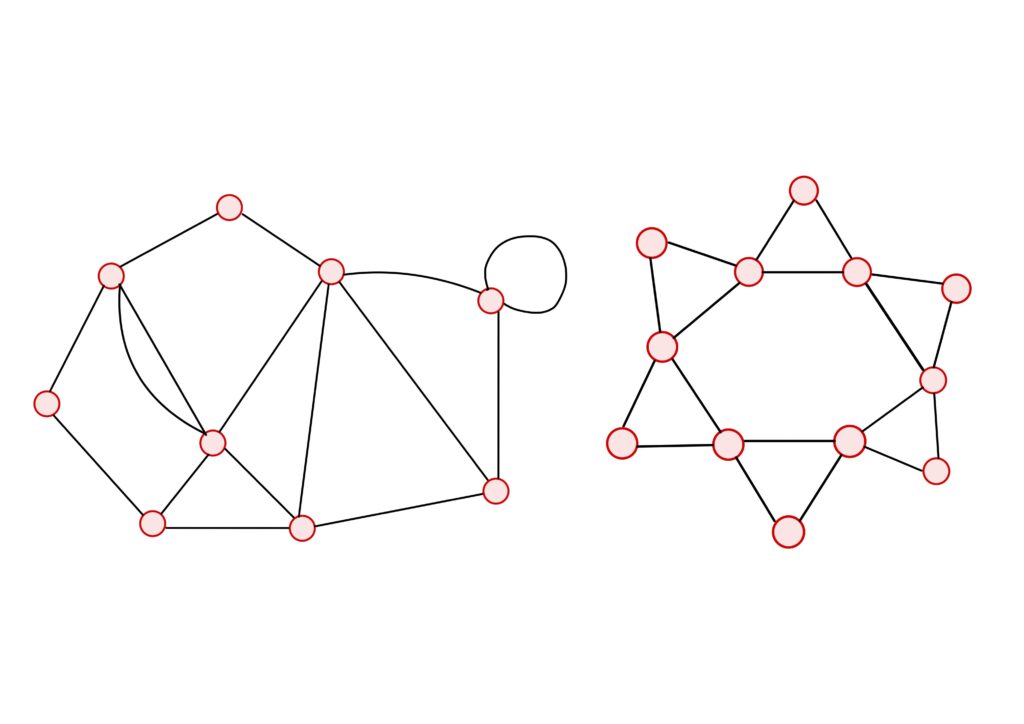
辺には、矢印で表される向きを考えることが出来ます。
そして各辺はちょうど2つの向きを持ちます。
向きが与えられた辺を有向辺(directed edge)といいます。
有向辺の矢印の根本にある頂点をこの有向辺の始点(origin)といい、矢印の先にある頂点を終点(termunus)といいます。
向きを考えない辺を無向辺といいます。
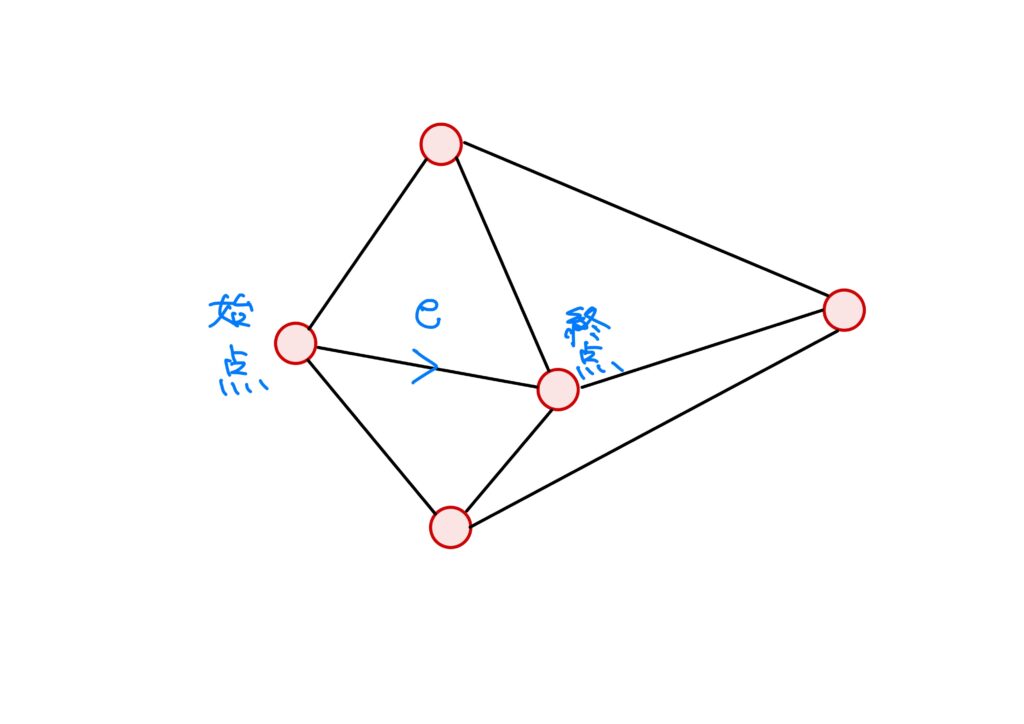
では、この「点と線からなるモノ」やら、始点、終点やらを数学的に表すにはどうすればよいでしょうか。
答えは簡単で、集合と写像の言葉を使って表現します。
数学的にグラフって何ですか?
では、「グラフとは何か?」という問に数学的に答えようと思います。
グラフ
集合\(V,E\)に対して、\(V\)と\(E\)の対\(X=(V,E)\)が以下を満たすとき\(X\)はグラフであるという。- \(V\cap E=\emptyset\)
- 次の性質を満たす写像\(i:E\to V\times V\)、\(\iota:E\to E\)が存在する。
- \(\iota^2\left(=\iota\circ\iota \right)={\rm id}_E\quad\)(ただし、\({\rm id}_E\)は\(E\)の恒等写像)
- 任意の\(e\in E\)に対して以下が成り立つ。 $$ \iota(e)\neq e,\quad i\left(\iota(e)\right)=\tau\left(i(e)\right) $$ ただし、\(\tau:V\times V\to V\times V\)は\(\tau(x,y)=(y,x)\)により定まる写像である。
これを見ても「ん?何いってんの?」となると思いますので、今まで述べていた図とどのようにつながるかを説明します。
図とのつながり
先のグラフの数学的な説明において\(V\)(vertexの頭文字)が頂点の集合、\(E\)(edgeの頭文字)が有向辺の集合に対応しています。
有向辺\(e\in E\)に対して、逆向きの有向辺を\(\bar{e}\)により表すことにすると、\(\bar{\bar{e}}=e\)が成り立ちます。
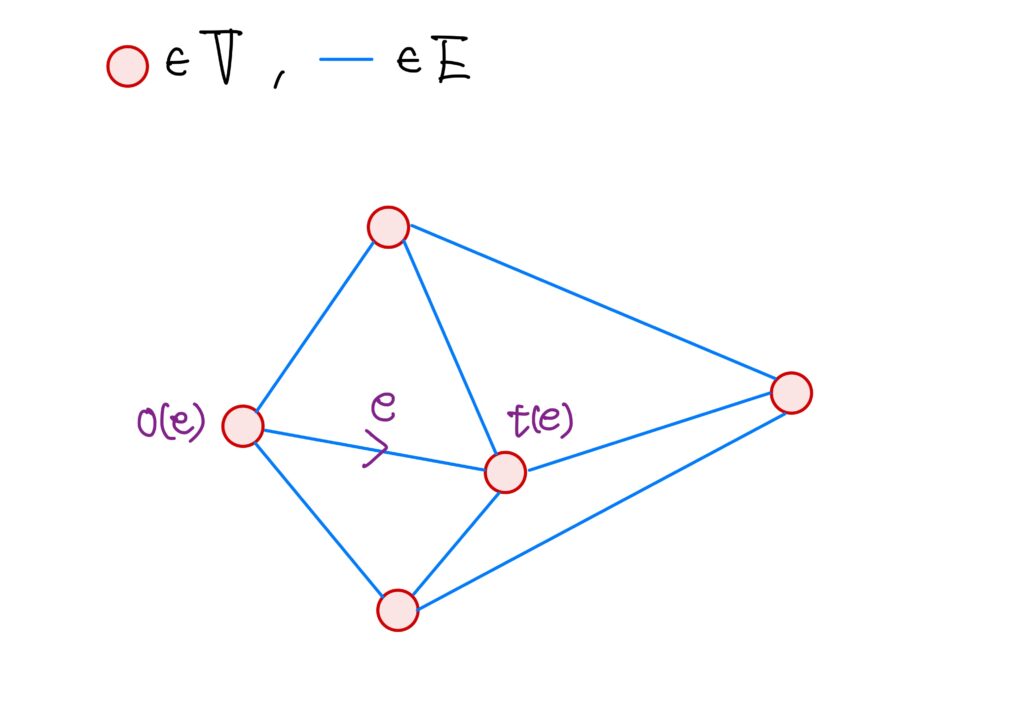
\(e\in E\)の始点を\(o(e)\)(\(o\)はoriginのo)、終点を\(t(e)\)(\(t\)はterminusのt)により表します。
辺の向きを逆にすれば、始点と終点が入れ替わるので、\(o(\bar{e})=t(e)\)、\(t(\bar{e})=o(e)\)が成り立ちます。
ここで、\(o,t\)は共に\(E\)から\(V\)の写像、すなわち\(o:E\to V\)、\(t:E\to V\)です。
この準備の元、\(i(e)=\left(o(e),t(e) \right)\)、\(\iota(e)=\bar{e}\)と置きます。
すなわち、写像\(i:E\to V\times V\)は辺と頂点の間の繋がり方を規定する写像であり、\(\iota: E\to E\)は有向辺の向きを逆向きにする写像です。
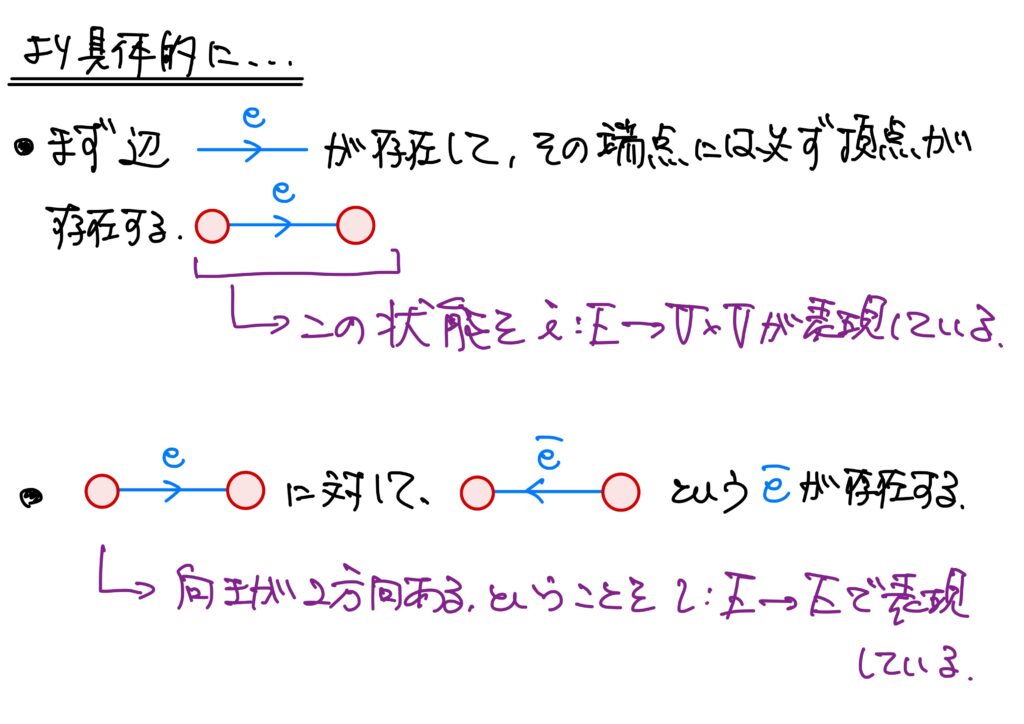
もう少し踏み込んでおくと、先に\(V\)は頂点の集合、\(E\)は有向辺の集合と述べましたが、頂点と有向辺を数学的に説明していません。
実は\(V,E\)はそれぞれ「なんであっても良い」のです。
ヒルベルト風に言えば、\(V\)は「椅子」の集合、\(E\)は机の集合であっても良いのです。
このような点やら辺やら線やらを無定義用語といいます。
つまり、ある対象が満たすべき性質によってそのものを定める、ということで、その性質を満たすものを点やら線と呼ぶということなのです。
故に、点やら線の中身(実態)が「椅子」やら「机」やらであっても何も問題ありません。
数学的な説明をしましたが…
今、グラフを数学的に説明しましたが、それに拘る必要は無いと思います。
というのも、実際筆者の知る限りですが、数学者はグラフを研究するときには、それを具体的な付として思い浮かべるようだからです。
とはいえ、数学的に記述することは重要ですけどね。
数学では、いくつかの特別な例たちに共通する概念を「構造」として取り出し、この「構造」そのものを研究対象とすることが多いです。
例えば、ベクトルやら行列やら、関数の空間などから取り出した「構造」は、「線型構造」と呼ばれるもので、この線形構造を扱う「線型代数」という分野が存在します。
また、形の対称性、「もの」の置換や変換などが持つ「構造」が、「群構造」と呼ばれるものです。
グラフも、ネットワーク、電気回路、乱歩などに現れる共通の概念を一般化した「構造」です。
それを一般的な枠組みの中で研究することで、その結果を特殊例にフィードバックする事ができます。
記号の話
\(E_x\)により\(x\)を始点とする有向辺\(e\)全体の集合を表します。
つまり、
\(x\)を始点とする有向辺の集合
$$ E_x=\left\{e\in E\middle|o(e)=x\right\} $$ とする。すなわち\(E_x\)は\(x\)を始点とする有向辺\(e\)全体の集合を表す。このとき、以下が成り立ちます。
命題2.
\(X=(V,E)\)をグラフとする。このとき\(x\neq y\)ならば、\(E_x\cap E_y=\emptyset\)である。すなわち、頂点が異なれば、その頂点を始点とする有向辺も異なる。命題2.の証明
背理法で証明します。
\(E_x\cap E_y\neq \emptyset\)とします。
このとき、ある要素\(e\in E_x\cap E_y\)が存在します。
\(o(e)=x\)、\(t(e)=y\)だから、\(x=y\)となって仮定に矛盾です。
命題2.の証明終わり
命題2.から
$$
E=\coprod_{x\in V}E_x
$$
(ただし、\(\coprod\)は交わらない和集合を指します)が成り立ちます。
グラフの応用例
グラフ理論の応用はたくさんあります。
四色問題
四色定理とは「如何なる地図も隣接する領域が異なる色になるように塗るには4色あれば十分である。」という定理です。
ただし、飛び地のような領域は考えません。
これはグラフ理論において「平面グラフは4彩色可能である」ということと同値です。
この問題は、グラフ理論における最も有名な未解決問題でしたが、1976年にケネス・アッペル(Kenneth Appel)とウルフガング・ハーケン(Wolfgang Haken)によってコンピュータを駆使して証明されました。

巡回セールスマン問題
巡回セールスマン問題(Traveling Salesman Problem, TSP)とは、多くのしと各市間の移動コストが与えられたとき、全ての市を一度だけ回って戻ってくるルートのうち最小のコストのものを求める問題です。
要するに、「一番楽ちんに回るにはどうすればいいか?」という問題です。
この問題は計算量が膨大だという意味で困難な問題として知られています。
余談
計算量が膨大と述べましたが、この問題は実質、線型計画法やら論理木を組み合わせた分枝限定法やら、線型計画法と巡回群を組み合わせた切除平面法により、約2000都市以内であれば、普通のパソコンでもおよそ1日以内で厳密解を得られることが多いようです。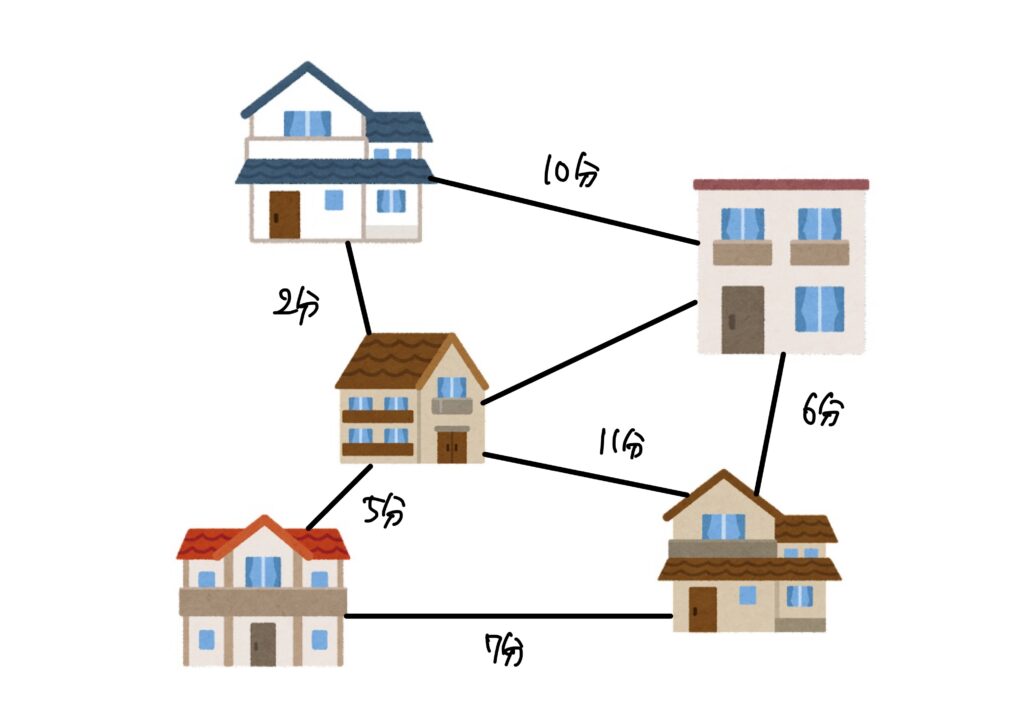
路線図
これは先の巡回セールスマン問題と似ているものですが、電車の路線図もグラフです。
もっと一般に交通網がグラフです。
この場合において最も身近だと思われるのが「乗り換えアプリ」です。
地域により異なると思いますが、首都圏にお住まいの方であれば日常的に使うのではないでしょうか。
乗り換えアプリは、始点(出発する駅)と終点(目的地の駅)を指定したとき、運賃や所要時間などの要素において最適なルートを検索しています。
首都圏にお住まいの方(ないしは居住経験がある方)はお分かりかと思いますが、電車は始点と終点をつなぐ路がいくつも存在します。
例えば、新宿駅⇔東京駅は中央線の他に丸ノ内線で行く、という手もあります。
他にもあるのでしょうが筆者は東京に住んでいないのでパッとは出てきません。ごめんなさい。
そして、新宿駅から東京駅に一駅で行けるわけではありません。
あらゆる駅を経由していきます。
その中で、どの路を通れば安く早いのか、ということを教えてくれるのが乗り換えアプリです。
これをグラフ理論の言葉を使うと、頂点が駅、辺が路線、路は辺の集まりです。
乗り換えアプリはまさにグラフ理論的視点でもって運用されているわけです。
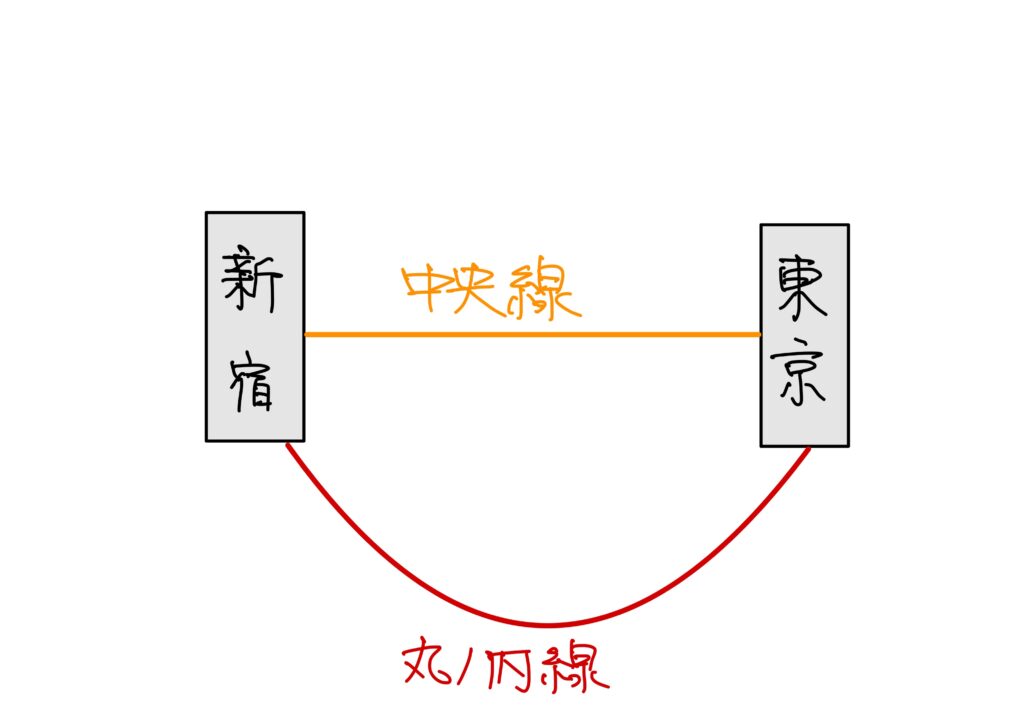
分子構造
これはシンプルです。
頂点が原子で辺が原子同士の結合を表しています(実は筆者はこの手の分野に近いことを研究していました)。
物質を構成する原子の繋がり方をグラフとして表現し、そのグラフの構造(どのように原子同士が結合しているか)という情報から物性を予測する、という研究もあるようです。

ネットワーク
グラフの図を見れば一目瞭然という感じですが、グラフ理論はネットワークの理論と大いに関係があります。
これは勿論通信におけるネットワークだけでなく、もっと一般に人間社会における人間の関係性を表すネットワークなども含む大きな意味でのネットワークです。
通信におけるネットワークは、最適な基地局配置に応用されています。
人間社会におけるネットワークの例を少し説明します。
1930年代、心理学者ヤコブ・モレノは社会学を発展させて、ソシオグラム(集団の中の人間関係や集団の様相を空間的にグラフとして表わしたもの)を発表しました。
モレノは
と発表しました。
ソシオグラムは以下のようなものです。
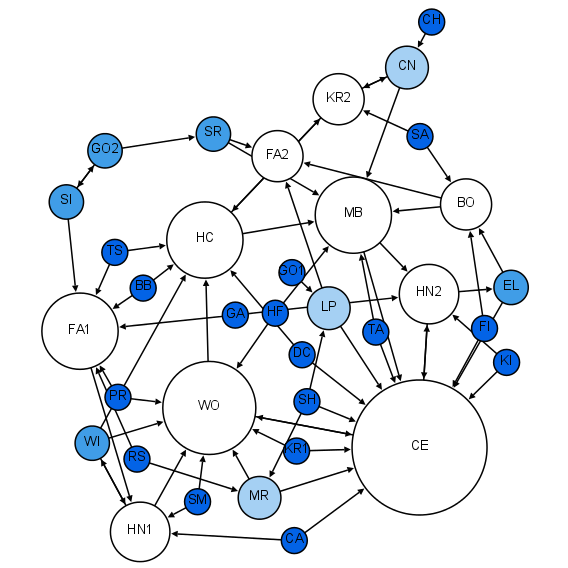
上図は、小学一年生の社会的構造の表象を表しています。
男子と女子はそれぞれ同性が友達でしたが、例外の1人の男子がが女子を好きだと言いましたが、相互的な関係ではないことが分かります。
ソシオグラムは現在では社会ネットワーク解析という分野に発展しています。
産業連関
産業の分野でもグラフ理論は活躍しています。
これは経済のお話ですが、経済にもグラフ理論が応用されています。
これについては後の記事で解説します(結構後になってしまいますが)が、ここでサラッと述べておきます。
- \(x_i\):部門\(i\)の生産量
- \(x_{ij}\):部門\(i\)の生産量から部門\(j\)により需要され、使われる量
- \(f_i\):部門\(i\)の生産量から消費財として需要され使われる量
- \(e_i\):部門\(i\)の生産量から海外(輸出)のために需要され、使われる量
- \(m_i\):部門\(i\)に輸入で海外から供給される量
とします。
ただし、農業部門には1を、工業部門には2を、サービス部門には3を対応させます。
これを表にまとめると次です。
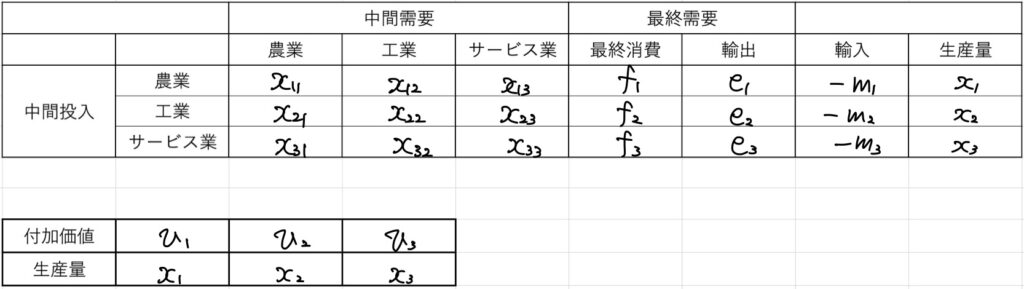
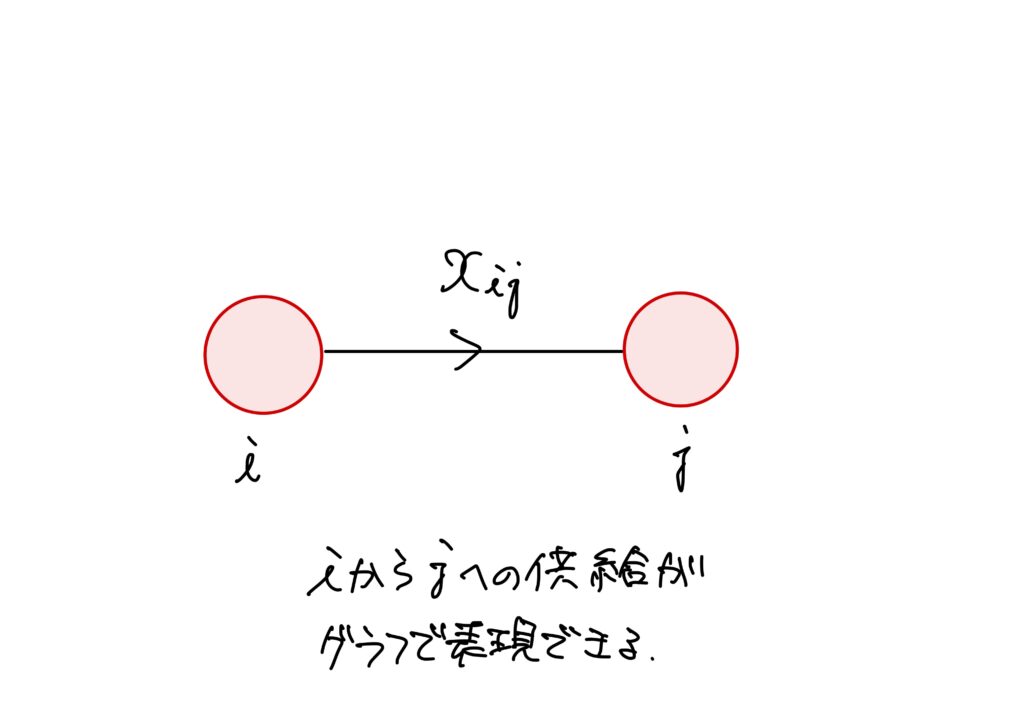
各部門を点、部門\(i\)から部門\(j\)への供給がある場合に点\(i\)と点\(j\)との間には辺が存在するとします。
そして、\(x_{ij}\)は部門\(i\)と部門\(j\)をつなげる辺に対応した値と捉えます。
そうすることで、グラフが出来上がります。
さらにこの応用とし、均衡産出高を考察するレオンチェフ方程式というものがあります。
皆様のコメントを下さい!
以前の記事でも述べましたが、グラフ理論は筆者が一番好きな分野です。
学部のときの講義で一番面白かった講義でした。
小中高大、または社会人になってからでも構いませんので、印象に残っている授業、講義があれば是非コメントで教えて下さい!
結
今回は、グラフ理論の初歩として「グラフとは何か?」ということとグラフ理論の応用例を解説しました。
くどいようですが、グラフ理論は筆者が好きな分野ということもあり、少し熱が入ってしまいました。
グラフというのは一言で言えば、
です。
これは集合と写像の言葉で表現することが出来ます。
応用例としては、四色問題、巡回セールスマン問題、路線図、分子構造、ネットワーク、産業連関など多岐にわたります。
次回は有限グラフ、正則グラフ、路について解説します。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!





コメントをする
為になります。非常に面白い