本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
では、問題
今回は前回の最後に「皆様への挑戦状」ということで提示した問題です。
図形の問題です。
\(\triangle ABC\)の\(\angle A\)の2等分線と\(BC\)の交点を\(D\)とするとき
$$
AB+AD=CD,\quad AC+AD=BC
$$
であるという。\(\angle B\)、\(\angle C\)はどんな角か求めてください。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13.
いざ、チャレンジ
チャレンジの結果…..解けました!
ただ、問題文の表現の仕方が納得しきれませんでした。
筆者の解答
\(\angle B=40^\circ\)、\(\angle C=20^\circ\)が筆者の解答です。
では、どのようにしてこの角を出したかを説明します。
まず、問題文の「”\(AB+AD=CD,\quad AC+AD=BC\)であるという。”」という表現ですが、「”であるという”?これは何?仮定?」と混乱しました。
「もしかして、\(AD\)が\(\angle B\)の二等分線であることをで\(AB+AD=CD,\quad AC+AD=BC\)と表現するという意味なのか?」とも思いましたが、そうすると「\(\angle B\)と\(\angle C\)はどんな角か。」という問題の意味が不明です。
今回における「〜であるという。」は「〜が成り立っているのだそうだ。」と捉えることもできなくもないということで、「おそらく仮定なのだろう」と仮定として話を勧めた結果、正解でした。
$$
AB+AD=CD\cdots①\\
AC+AD=BC\cdots②
$$
により、\(AD\)を消去すると、
$$
AC-AB=BC-CD=BD
$$
と分かります。
ここで、\(AB\)を\(B\)の方向に伸ばして、半直線\(AB\)上に\(BE=BD\)となるように点\(E\)を取れば、\(AE=AC\)となります。
故に、\(\triangle BED\)は二等辺三角形なので、\(\angle BDE=\angle AED\)です。
従って、\(\angle B=\angle ABD=\angle BDE+\angle AED=2\angle AED\)です。

さて、\(\triangle AED\)と\(\triangle ACD\)に着目してみます。
今、\(AE=AC\)であり、\(AD\)は共通、線分\(AD\)が\(\angle A\)の二等分線なので\(\angle EAD=\angle CAD\)です。
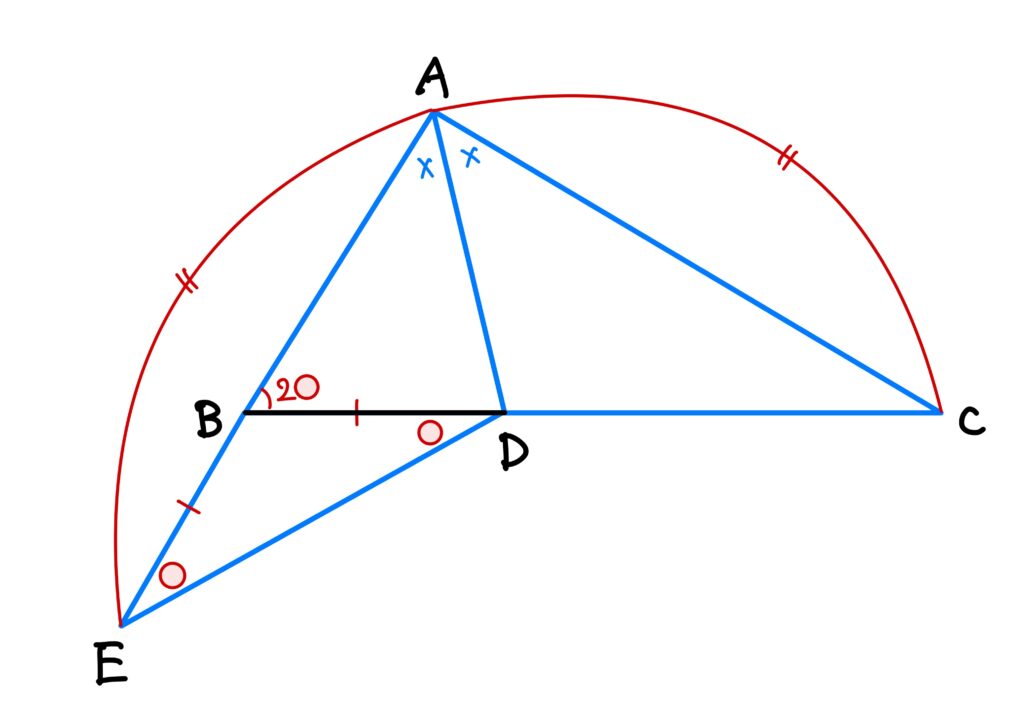
従って、二辺狭角が合同(中学校では「二辺とその間の角が等しい」と習います)なので、\(\triangle AED\equiv\triangle ACD\)です。
故に、\(\angle AED=\angle ACD\)です。
ここで、\(\angle C=\angle ACB=c\)とすると、\(\angle B=\angle ABC=2c\)です。
つまり、\(\angle B\)と\(\angle C\)の間には\(\angle B=2\angle C\)という関係がある、ということです。
さらに、\(\displaystyle\angle ADB=90^\circ-\frac{c}{2}\)と分かります。
線分\(BC\)上に\(CF=AC\)となるように点\(F\)を取れば、\(AC+AD=BC\)だから、
$$
BF=BC-CF=BC-AC=AD
$$
となります。
また、\(CF=AC\)によって\(\displaystyle\angle AFD=90^\circ-\frac{c}{2}\)だから、\(\angle ADF=\angle AFD\)です。
故に、\(AF=AD=BE\)なので、\(\angle FAB=\angle FBA=2c\)だから
$$
\angle AFC=2c+2c=4c
$$
となります。
また、\(\displaystyle\angle AFC=90^\circ-\frac{c}{2}\)なので、\(\displaystyle4c=90^\circ-\frac{c}{2}\)だから\(c=\angle C=20^\circ\)となります。
従って、\(\angle B=40^\circ\)です。
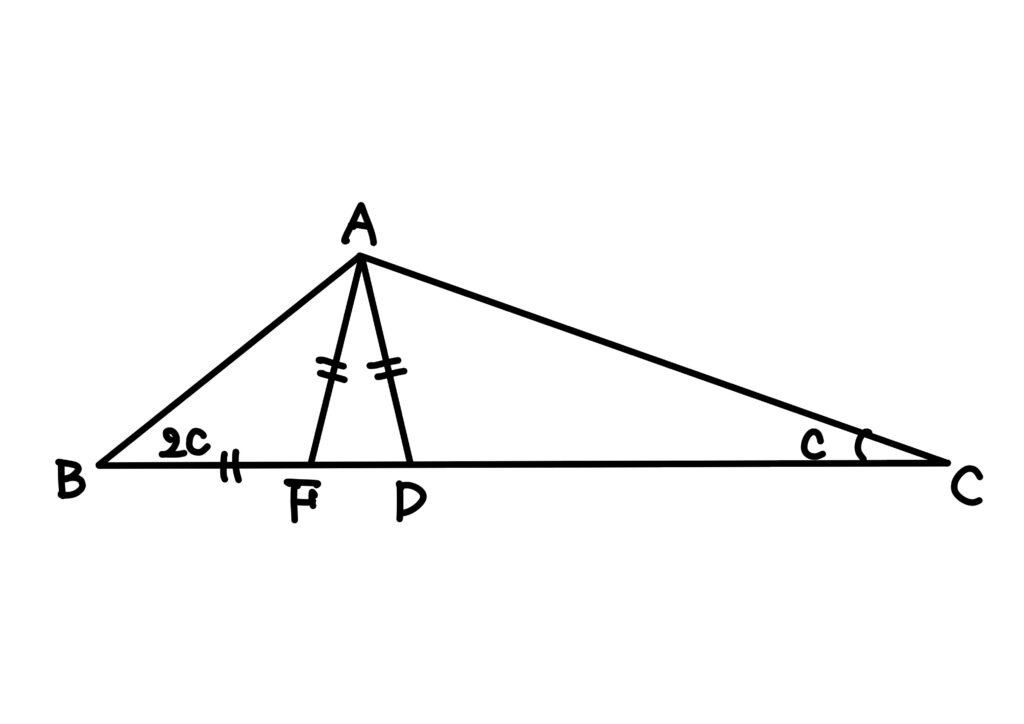
投稿されたエレガントな解答
では、投稿された解答を紹介します。
ただし、\(\angle B=2\angle C\)の証明は省略します。
$$
AB+AD=CD\qquad(1)\\
AC+AD=BC\qquad(2)
$$(中略)
\(BC\)上に\(F\)を\(\angle FAC=\alpha\)にとれば\(AF=CF\)。また、\(\angle AFB=2\alpha=\angle B\)より\(AB=AF\)である。よって\(AB=AF=CF\)。
これと(1)より
$$
DF=CD-CF=CD-AB=AD.
$$
ゆえに\(\angle DAF=\angle DFA=2\alpha\)、したがって
$$
\angle BAD=\angle DAC=2\alpha+\alpha=3\alpha.
$$
よって\(\angle BAC=\angle BAD+\angle DAC=6\alpha\)。
\(\triangle ABC\)の内角の和は\(180^\circ\)であるから
$$
\angle A+\angle B+\angle C=6\alpha+2\alpha+\alpha=180^\circ.
$$
これから\(\alpha=20^\circ\)、よって\(\angle B=40^\circ\)、\(\angle C=20^\circ\)。以下の解では\(\angle B=2\angle C\)の証明は省略する。
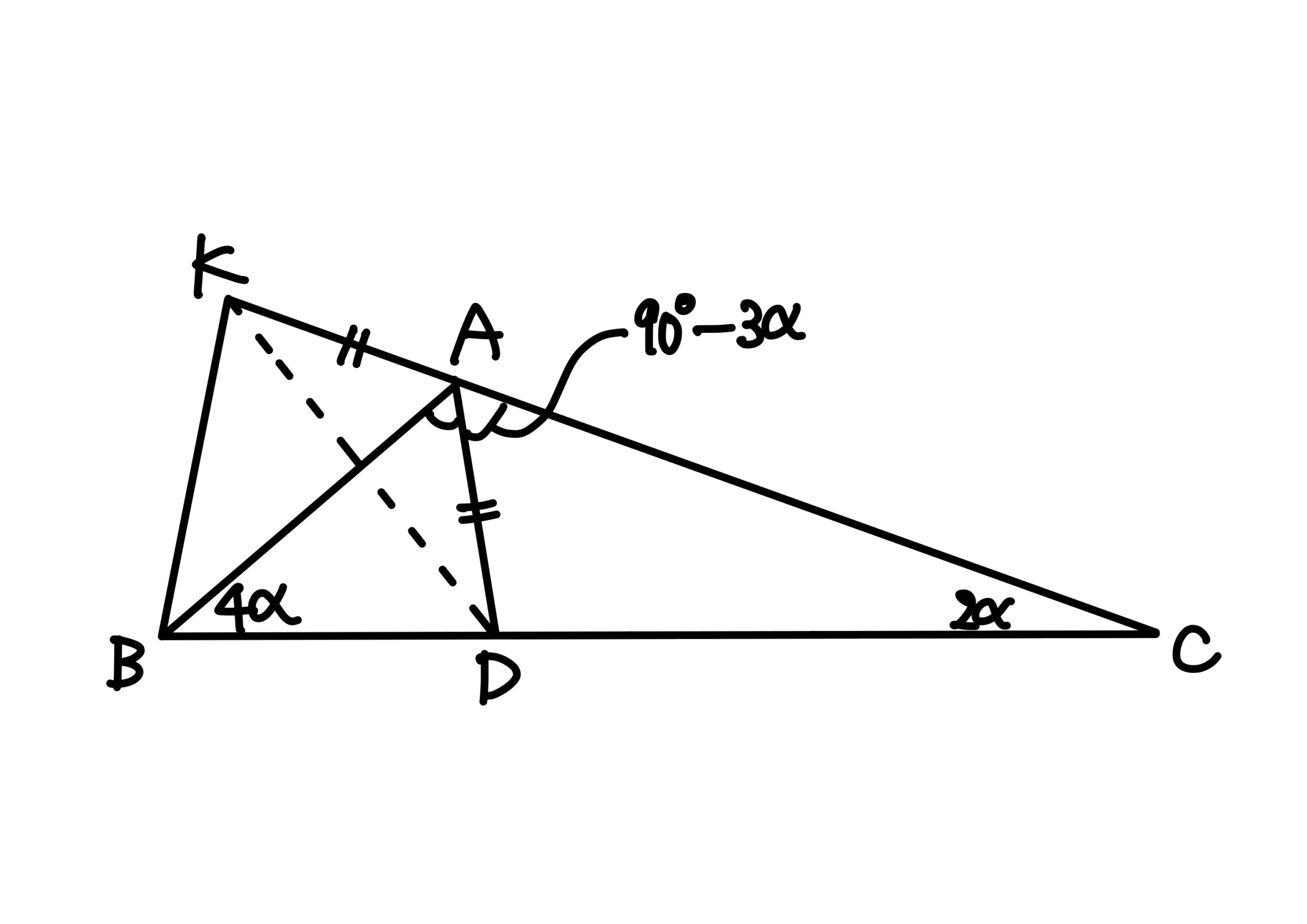
解2 \(\angle C=2\alpha\)とおけば\(\angle B=4\alpha\)である。
\(\angle BAC=180^\circ-6\alpha\)であるから
$$
\angle BAD=\angle DAC=90^\circ-3\alpha.
$$
\(CA\)の延長上に点\(K\)を\(AK=AD\)にとれば、\(AC+AD=BC\)だから
$$
CK=AC+AK=AC+AD=BC.
$$
よって\(\angle CKB=\angle CBK=90^\circ-\alpha\)。
また\(\angle ADB=\angle DAC+\angle C=90^\circ-3\alpha+2\alpha=90^\circ-\alpha\)より、
$$
\angle AKB=\angle ADB.
$$
ここで\(AK=AD\)より
$$
\angle AKD=\angle ADK.
$$
2式の両辺を辺々相減じて
$$
\angle BKD=\angle BDK.
$$
よって\(BK=BD\)。したがって\(\triangle KAB\equiv\triangle DAB\)となるから
$$
\angle KAB=\angle DAB=\angle DAC,
$$
よって\(3\angle KAB=180^\circ\)。ゆえに\(\angle KAB=60^\circ\)。
\(\angle KAB=\angle B+\angle C=6\alpha\)だから
$$
\alpha=10^\circ.
$$
したがって、\(\angle B=40^\circ\)、\(\angle C=20^\circ\)である。解4 (中略)
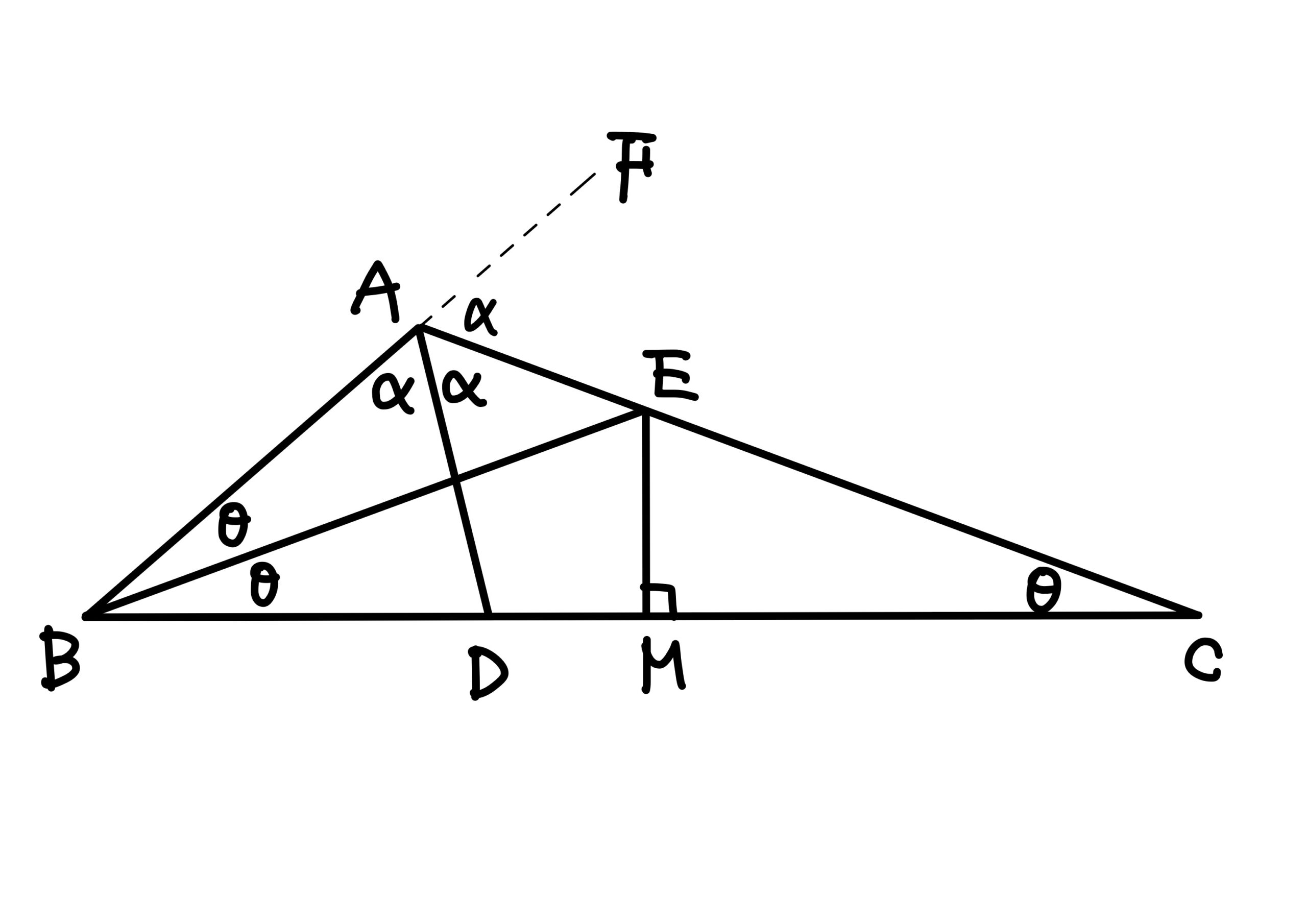
\(\angle C=\theta\)とおけば\(\angle B=2\theta\)である。\(\angle B\)の2等分線と\(AC\)との交点を\(E\)とすれば、\(\angle EBC=\angle ECB\)であるから、\(E\)から\(BC\)への垂線の足を\(M\)とすれば、\(M\)は\(BC\)の中点である。
よって\(AB+AD=CD\)より
$$
AB+AD+BD=CD+BD=BC=2BM.
$$
\(BM\)は\(\triangle ABD\)の周の半分であるから、\(M\)は\(\triangle ABD\)の\(\angle B\)内の傍接円が\(BD\)に接する点で、\(M\)において\(BD\)に立てた垂線と\(\angle B\)の2等分線との交点\(E\)は傍心である。よって\(EA\)は\(\angle BAD\)の外角を2等分する。\(\angle BAD=\angle DAC=\alpha\)とおき、\(BA\)の延長上の点を\(F\)とすれば、\(\angle FAC=\angle DAC=\alpha\)であるから\(3\alpha=\angle BAF=180^\circ\)。ゆえに\(\alpha=60^\circ\)。
\(\angle FAC=2\theta+\theta=3\theta\)であるから\(\theta=20^\circ\)。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p81-p83.
よって\(\angle B=40^\circ\)、\(\angle C=20^\circ\)である。
解4の傍接円を使う、というのはものすごい発想だと思いました。
筆者の中ではもはや傍心すらうろ覚えでした。
図形の問題は発想で誠にシンプルに問題を解けたりするところが面白いところですよね。
読者の皆様への挑戦状!
今から紹介する問題の解答は来週解説します!
正三角形\(ABC\)の辺\(BC\)上に点\(D\)を、\(BD:DC=2:1\)にとり、線分\(AD\)上に点\(E\)を\(AE:ED=3:4\)にとれば、\(\angle BED\)、\(\angle CED\)はそれぞれどんな角になるでしょうか。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
今回の問題は図形の問題で、少し頭を捻る問題でしたがシンプルな問題に感じました。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!




コメントをする