本記事の内容
本記事は、位数が12の群の分類の一部分について解説する記事です。
本記事を読むに当たり、商群、二面体群、生成された部分群、シローの定理について知っている必要があるため、以下の記事も合わせて御覧ください。
↓商群の記事
↓二面体群の記事
↓生成された部分群の記事
↓シローの定理の記事
今回から数回に渡ってやること
今回から数回に渡って何を解説するか、というと、結論としては次の定理の証明です。
定理0.
\(G\)が群で、\(\left|G\right|=12\)であれば、\(G\)は次の1.から5.のどれかと同型である。また、1.から5.の中で自分以外と同型になるものは存在しない。- \(\mathbb{Z}/{3\mathbb{Z}}\times\mathbb{Z}/{4\mathbb{Z}}\left(\cong \mathbb{Z}/{12\mathbb{Z}} \right)\)
- \(\mathbb{Z}/{3\mathbb{Z}}\times\mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{2\mathbb{Z}}\)
- 交代群\(A_4\)
- 二面体群\(D_6\)
- \(\left\langle x,y\middle|x^4=y^3=1,\ xy=y^2x\right\rangle\)
「なぜ12なの?」と思うかも知れませんが、12という数を選んだのは、位数が小さい群の中では位数12の群が一番興味深いと言われているからです。
また、分類の過程で群論に関して今までに学んだことのほとんどを使うことになるからです。
要するに、位数12の群は群論の基礎知識をフル稼働させるため、群論の全体像をつかみやすくするだけでなく「群のイロハが詰まっている」という理想的な状況なのです。
交代群
一言で述べれば、
です。
\(\sigma\)を置換とし、\({\rm sgn}(\sigma)\)を\(\sigma\)の符号とすると、\({\rm sgn}\)は\(\mathcal{G}_n\)から\(\left\{\pm1\right\}\)への準同型写像となります。
\(A_n={\rm Ker}({\rm sgn})\)(準同型写像\(\varphi\)の核\({\rm Ker}(\varphi)\)は正規部分群でしたね)と書き、\(A_n\)のことを\(n\)次交代群といいます。
定理0.の証明の流れ
割とシンプルです。
- ① 出現する全ての群が同型でないことの証明
- ② \(G\)が位数12の群なら、1.から5.のうちのどれかと同型になることの証明
- 1.と同型になる場合
- 2.と同型になる場合
- 3.と同型になる場合
- 4.と同型になる場合
- 5.と同型になる場合
今回は、①と、②を証明するためのちょっとした準備を行います。
いざ、証明(Part.1)
主張を再掲しておきます。
定理0.
\(G\)が群で、\(\left|G\right|=12\)であれば、\(G\)は次の1.から5.のどれかと同型である。また、1.から5.の中で自分以外と同型になるものは存在しない。- \(\mathbb{Z}/{3\mathbb{Z}}\times\mathbb{Z}/{4\mathbb{Z}}\left(\cong \mathbb{Z}/{12\mathbb{Z}} \right)\)
- \(\mathbb{Z}/{3\mathbb{Z}}\times\mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{2\mathbb{Z}}\)
- 交代群\(A_4\)
- 二面体群\(D_6\)
- \(\left\langle x,y\middle|x^4=y^3=1,\ xy=y^2x\right\rangle\)
1.から5.の全ての群が同型でないことの証明
1.と2.は可換群で、3.から5.は非可換群なので、1.または2.が3.から5.のどれかと同型になることはありません。
1.には位数4の要素があり、2.には位数4の要素がないので、1.と2.は同型ではありません。
交代群\(A_4\)に対して、\((i_1\ i_2\ i_3)\)という形の巡回置換の数は\(\left\{1,2,3,4\right\}\)から3個の数字を選ぶ選び方の数4個と、3個の数字の巡回置換の数2の積8個です。
それ以外にクラインの四元群(【代数学の基礎シリーズ】群論編 その19参照)の要素4個が存在するため、合計で12個となり、それ以外の要素は存在しません。
故に、\(A_4\)に位数4の要素は存在しません。
ここで、二面体群の性質を使います。
命題1.
- 関係式\(t^n=I_2\)(ただし、\(I_2\)は\(2\)次元の単位行列)、\(r^2=I_2\)、\(rtr=t^{-1}\)が成り立つ。
- \(\left|D_n\right|=2n\)、\(D_n=\left\{I_2,t,\dots,t^{n-1},r,rt,\dots,rt^{n-1}\right\}\)である。
- \(rt^i\ (i=0,\dots,n-1)\)の位数は\(2\)である。
命題1.の証明は【代数学の基礎シリーズ】群論編 その12を御覧ください。
命題1.により、\(D_6\)の要素の位数は6の約数です。
したがって、3.と4.には位数4の要素が存在しません。
しかしながら、5.には位数4の要素が存在していることから、3.または4.が5.と同型になることはありません。
また、3.には位数6の要素は存在しませんが、4.には存在しているため、3.と4.は同型ではありません。
以上のことから、1.から5.の中で同型になるものがないことが示されました。
1.から5.の全ての群が同型でないことの証明終わり
次に、\(G\)が位数12の群なら、1.から5.のうちのどれかと同型になることを証明するためのちょっとした準備を行います。
準備(シロー\(p\)部分群に着目)
とします。
このとき、次の事実を使います。
命題2.
\(G\)が有限群で、\(\left|G\right|=p^2\)(\(p\)は素数)ならば、\(G\)は可換群である。命題2.の証明は【代数学の基礎シリーズ】群論編 その24を御覧ください。
\(\left|H\right|=4=2^2\)なので、命題2.により\(H\)は可換群です。
\(H\)が位数4の要素を持てば、\(H\cong\mathbb{Z}/{4\mathbb{Z}}\)です。
\(H\)が位数4の要素を持たなければ、単位元以外の要素の位数は2です。
\(a\neq b\in H\)を単位元以外の要素とすると、\(ab\neq a,b\)です。
\(ab=1\)なら、\(b=a^{-1}=a\)なので矛盾です。
したがって、\(H=\left\{1,a,b,ab\right\}\)となり、\(H=\left\langle a,b\right\rangle\)です。
\(H_1=\left\langle a\right\rangle=\left\{1,a\right\}\)、\(H_2=\left\langle b\right\rangle=\left\{1,b\right\}\)とすれば、\(H_1\cap H_2=\left\{1\right\}\)であり、\(H\)は可換群なので、\(H_1,H_2\)は\(H\)の正規部分群です。
\(H_1H_2=H\)なので、\(H\cong H_1\times H_2\cong \mathbb{Z}/{2\mathbb{Z}}\times \mathbb{Z}/{2\mathbb{Z}}\)です。
\(12\div 3=4\)なので、\(K\)の共役の個数は1か2か4です。
\(2\equiv1\ ({\rm mod}\ 3)\)なので、\(K\)の共役の個数は2ではありません。
\(K\)が正規部分群でないと仮定して、\(H\)が正規部分群であることを示します。
仮定から、\(K\)の共益の数は4です。
\(K_1,\dots,K_4\)を\(K\)の共役とします。
\(i\neq j\)なら、\(K_i\cap K_j\subsetneqq K_i\)ですが、\(\left|K_i\right|=3\)は素数なので、\(K_i\cap K_j=\left\{1\right\}\)です。
故に、\(S=\displaystyle\bigcup_{i=1}^4\left( K_i\setminus \left\{1\right\}\right)\)とおくと、\(\left|S\right|=8\)であり、\(S\)の要素は全て位数3の要素です。
位数が2、4の要素は\(G\setminus \left( S\cup\left\{1\right\}\right)\)の要素になりますが、\(\left|G\left( S\cup\left\{1\right\}\right)\right|=3\)なので、\(H\)の共役の可能性としては\(G\setminus S\)しかありえません。
したがって、\(H\)は正規部分群です。
準備おしまい
皆様のコメントを下さい!
続きです。
今回はユードクソスの「無限」の取り扱いについて少々お話します。
古代ギリシャの思想家が悩んだ「無限」をどう取り扱うのか?ということは、数学に関する限り、ユードクソスによって解決されました。
ある線分の半分以上を取り去り、残りからさらにその半分を取り去る。これを繰り返すとその残りの部分は予め指定された線分よりちいさくなる
これを現代的に言い換えれば、「正数列\(\{a_n\}_{n\in\mathbb{N}}\)が
$$
a_{n+1}\leq\frac{1}{2}a_n
$$
を満たしていると、\(a_n<a\)が予め指定された正数\(a\)に対して成り立つような\(n\)が存在する」ということです。
ユードクソスは「取り尽くしの方法」と背理法を結びつけることにより、円の面積や三角錐の体積を求めました。
その後、ユー ドクソスのアイディアはアルキメデスにより発展され、球面や放物線の研究に使われました。
しかし、ヨーロッパではアルキメデスの業績は忘れ去られたのです。
これは、アラビアから「再輸入」されるまで、ギリシャ数学が1000年の間忘れられていたことを思い起こせば不思議なことではありません。
ユードクソスのアイディアは、無限のプロセス、あるいは無限そのものが現れる数学の事柄を、有限の言葉でいい表そうとする「有限主義」や「形式主義」の端緒になるのです。
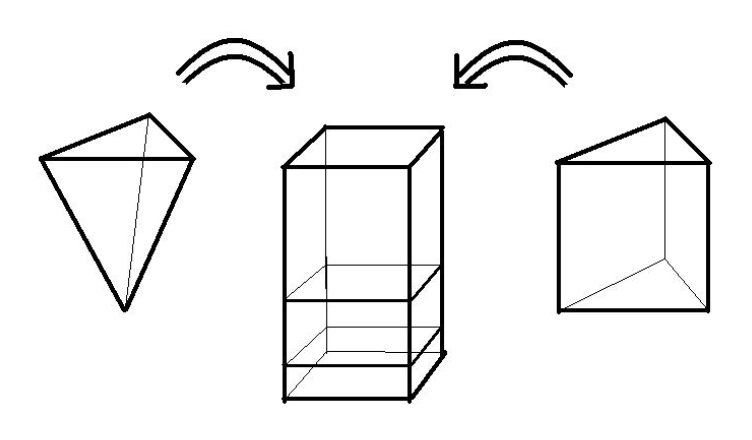
ユードクソスの論法を満ちいて三角錐(四面体)の体積を求めてみましょう。
ただし、斜角柱の体積が底面積\(\times\)高さであることは既知とします。
(1)まず底面積と高さがそれぞれ等しい2つの三角錐の体積が等しいことを証明します。
2つの三角錐(の体積)を\(V\)と\(W\)とします。
\(V>W\)と仮定しましょう。
\(V\)の方に注目して(\(V<W\)の場合は\(W\)に注目)、図のように\(V\)を分割します(2つの\(V_1\)と\(P,P^\prime\))。
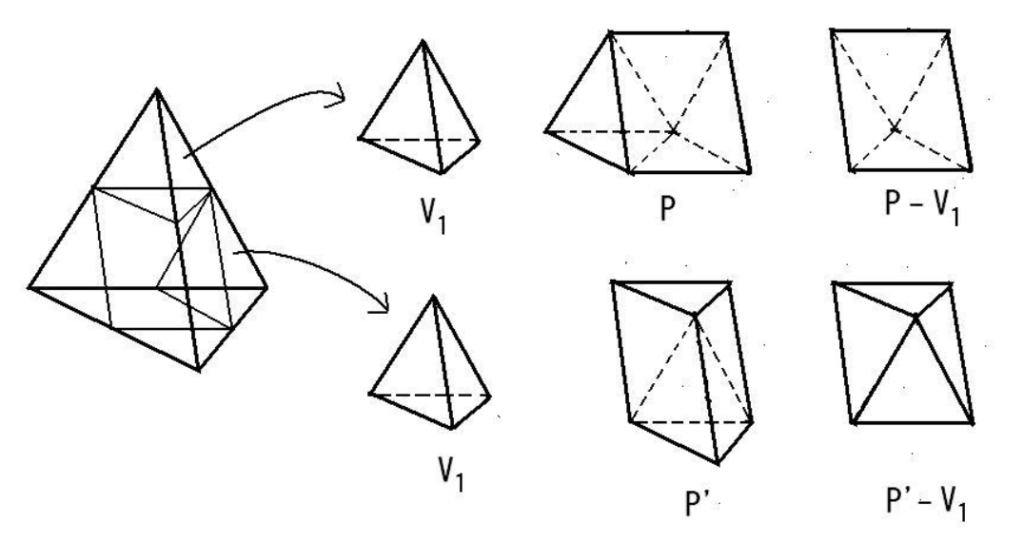
少三角錐の体積を\(V_1\)で表すことにします。
\(V\)には\(V_1\)が4つ入るから\(V>4V_1)となります。
一 方、2つの\(V_1\)を除いた残りは二つの角柱\(P\)と\(P^\prime\)になり、\(P\)から\(V_1\)を除いた多面体と、\(P^\prime\)から\(V_1\)を除いた多面体は合同です。
よって\(P\)と\(P^\prime\)の体積は等しいです。
角柱\(P^\prime\)の体積は\(V\)の底面積の\(\displaystyle\frac{1}{4}\)(\(P^\prime\)の底面積)と\(V \)の高さの\(\displaystyle\frac{1}{2}\)(\(P^\prime\)の高さ)をかけたものに等しいから、結局\(P\)と\(P^\prime\)を合わせた多面体の体積\(P_1\)は\(V\)の底面積と高さで決まります。
\(V\)は2つの\(V_1\)と\(P_1\)の和だから、
$$
V=2V_1+P_1
$$
を得ます。
三角錐\(V_1\)の底面積は\(V\)の底面積の\(\displaystyle\frac{1}{4}\)であり、高さは\(V\)の高さの\(\displaystyle\frac{1}{2}\)ということに注意しましょう。
2つの小三角錐\(V_1\)に対して同様の分割を行い、これを続けていきます。
\(V_n\)を\(n\)回目に得られる小三角錐の体積とすると、
$$
V>4^nV_n,\quad V=2^nV_n+P_n
$$
という式が得られます。
ただし、\(P_n\)は\(V\)の底面積と高さで決まる量です。
故に、
$$
V<2^{-n}V+P_n
$$
です。
\(W\)に対しても同様のことを行うと、\(W\)の底面積と高さで決まる量\(Q_n\)により
$$
W=2^nW_n+Q_n(>Q_n)
$$
と表されます。
仮定から、\(V\)の底面積と高さは\(W\)の底面積と高さにそれぞれ等しいから\(P_n=Q_n\)です。
故に、
$$
V-W<\left( 2^{-n}V+P_n\right)-Q_n=2^{-n}V\tag{\ast}
$$
となります。
一方で、ユードクソスの論法を適用すれば、
$$
2^{-n}V<V-W
$$
を満たす番号\(n\)が存在するから、これは\((\ast)\)に矛盾です。
したがって、\(V=W\)でなければなりません。
今回はここまでです。
次回は三角錐の体積が底面積\(\times\)高さ\(\div 3\)であることを示します。
如何でしたか?
古代ギリシャの数学のレベルというものは計り知れないですね。
古代ギリシャの数学事情について「これ、知ってる?」というものがあれば是非コメントで教えて下さい!
結
今回は位数が12の群の分類の一部を解説しました。
位数12の群は位数自体が比較的小さく、そして群論の知識をフル稼働で使うため群論そのものの良い復習となるだけでなく、群論の見通しを良くします。
個人的に最も面白いのは、位数12の群はたった5つのグループに分けることができる、ということです。
状況に応じて考えやすい同型な群で話をすすめることができます。
次回は今回の続きとして、各群と同型になる場合を証明していきます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。







コメントをする
交代群の説明の部分は、An=Ker(sgn)ではありませんか?
名無しさん
ご指摘ありがとうございます!
間違っておりました。修正いたしました。
「しかしながら、5.には位数6の要素は存在しませんが、4.には存在するので、3.と4.は同型ではありません。」ここちょっと文が壊れているように思います。「5が3、4どちらとも同型でない」「3と4が同型でない」の2つの説明が混ざってしまったのでしょうか。
名無し様
コメントありがとうございます。
>「しかしながら、5.には位数6の要素は存在しませんが、4.には存在するので、3.と4.は同型ではありません。」ここちょっと文が壊れているように思います。「5が3、4どちらとも同型でない」「3と4が同型でない」の2つの説明が混ざってしまったのでしょうか。
とのことでしたが、ご指摘のとおりでした。
訂正いたしました。ありがとうございました。