「対称群の共役類①〜準備〜(対称群の復習とヤング図形)」【代数学の基礎シリーズ】群論編その18

本記事の内容
巡回置換の復習
置換群(対称群)の復習
ヤング図形
皆様のコメントを下さい！
結

本記事の内容

本記事は、対称群の共役類を語るための準備として、巡回置換を復習し、その性質を解説する記事です。

本記事を読むに当たり、巡回置換について知っている必要があるため、以下の記事も合わせてご覧ください。

巡回置換の復習

巡回置換を一言で。

番号がぐるぐる回る(巡回する)置換のこと。

巡回置換とは？

巡回置換

m, n \in N

$m,n\in\mathbb{N}$ が

$m<n$ を満たし、

$M_n=\{1,2,\dots,m,\dots,n\}$ とする。また、

$\sigma= \begin{pmatrix} 1&2&\cdots&m&m+1&\cdots&n \\ i_1&i_2&\cdots&i_m&i_{m+1}&\cdots&i_n\\ \end{pmatrix}$ とする。このとき、置換

$\sigma$ が

$M_n$ の要素のうち、

$i_1,i_2,\dots,i_m$ 以外は動かさず

$i_1,i_2,\dots,i_m$ のみを

$i_1\mapsto i_2,\ i_2\mapsto i_3,\cdots,i_m\mapsto i_1$ のように一巡させる置換であるとき、すなわち

$\sigma= \begin{pmatrix} i_1&i_2&\cdots&i_m&i_{m+1}&\cdots&i_n \\ i_2&i_3&\cdots&i_1&i_{m+1}&\cdots&i_n\\ \end{pmatrix}$ を巡回置換といい、

$\sigma=(i_1\ i_2\ \cdots\ i_m)$ で表す。

例

例1.
$\sigma= \begin{pmatrix} 1&2&3&4&5 \\ 5&2&1&4&3\\ \end{pmatrix}$
とします。
このとき、
$\sigma(1)=5,\ \sigma(2)=2,\ \sigma(3)=1,\ \sigma(4)=4,\ \sigma(5)=3$
で、 $2$ と $4$ は順番を並び替えずに、 $1\mapsto 5$ 、 $5\mapsto 3$ 、 $3\mapsto 1$ というように、 $1$ が $5$ と $3$ を経由してグルッと回ってて $1$ に戻ってくるということです。
それ故、巡回置換と呼ばれます。

置換は巡回置換の積で表すことができます。

定理2.

任意の置換は共通の文字を含まないいくつかの巡回置換の積として表され、この表し方は積の順序を除いて一意的である。

定理2.の証明は【線型代数学の基礎シリーズ】行列式編その1を御覧ください。

置換群(対称群)の復習

置換群(対称群)

$X$ の置換全体からなる群のことを

$X$ の置換群という。

$X_n=\left\{1,2,\dots,n\right\}$ とするとき、

$X_n$ の置換のことを $n$ 次の置換という。

$n$ 次の置換全体よりなる群のことを

$\mathcal{G}_n$ で表し、

$\mathcal{G}_n$ を $n$ 次対称群という。

さも当然のように、「置換全体からなる群」と置換全体からなる集合は群となると述べていますが、置換は全単射な写像なので、写像の合成でもって群です。

ちなみに、置換とは以下でした。

置換

$n\in\mathbb{N}$ とする。

$n$ 個の文字

$1,2,\dots,n$ からなる集合を

$M_n=\{1,2,\dots,n\}$ とする。写像

$\sigma:M_n\to M_n$ が全単射であるとき、

$\sigma$ を

$M_n$ の置換という。
　置換

$\sigma$ による対応が

$1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n$ であるとする、すなわち、

$\sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n$ とする。このとき

$\sigma$ を

$\sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$ と書く。

詳しくは【線型代数学の基礎シリーズ】行列式編その1を御覧ください。

ヤング図形

巡回置換の型

$l$ 個の数の巡回置換 $i_1\ \cdots\ i_l$ を、長さ $l$ の巡回置換といいます。
$\sigma$ を共通する要素の無い巡回置換の積に書くとき、長さが大きい順に
$\sigma=(i_{11}\ \cdots\ i_{1l_1})\cdots(i_{t1}\cdots i_{tl_t})\quad l_1\geq l_2\geq\cdots\geq l_t$
と表すことが出来ます。
このとき、 $(l_1,\cdots,l_t)$ を $\sigma$ の型と呼ぶことにします。
例えば、 $\sigma\in\mathcal{G}_{10}$ で $\sigma=(1\ 2\ 3\ 4)(5\ 6\ 7)(8\ 9)$ なら、 $\sigma$ の型は $(4,3,2,1)$ です。

ヤング図形とは？

$\mathcal{G}_n$ の要素の置換の型は次のような図形で表すことが出来ます。

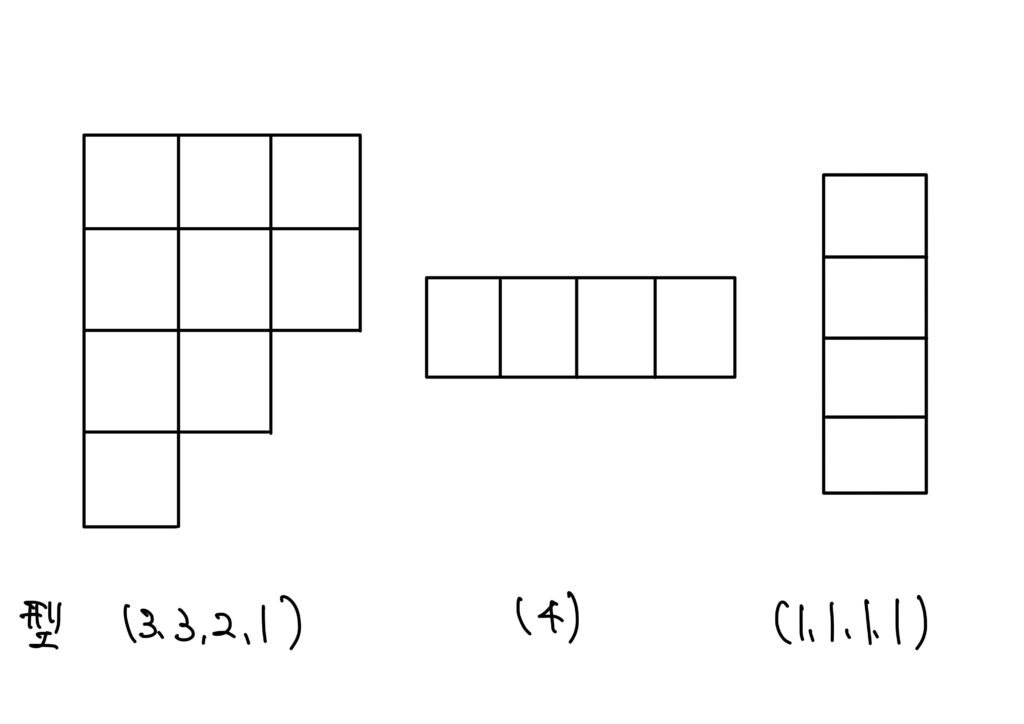
このような図形をヤング(Young)図形といいます。
例えば、一番左のヤング図形に対応する型は $(3,3,2,1)$ です。
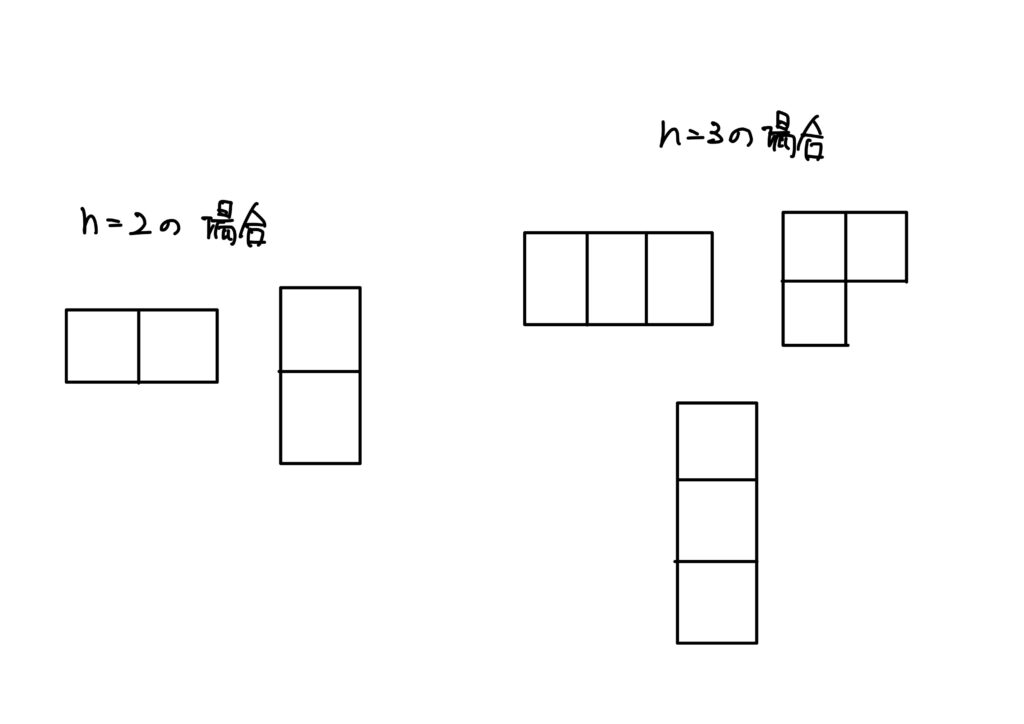
$n=2,3$ の場合のヤング図形はそれぞれ $2,3$ 個あり、以下のようになります。

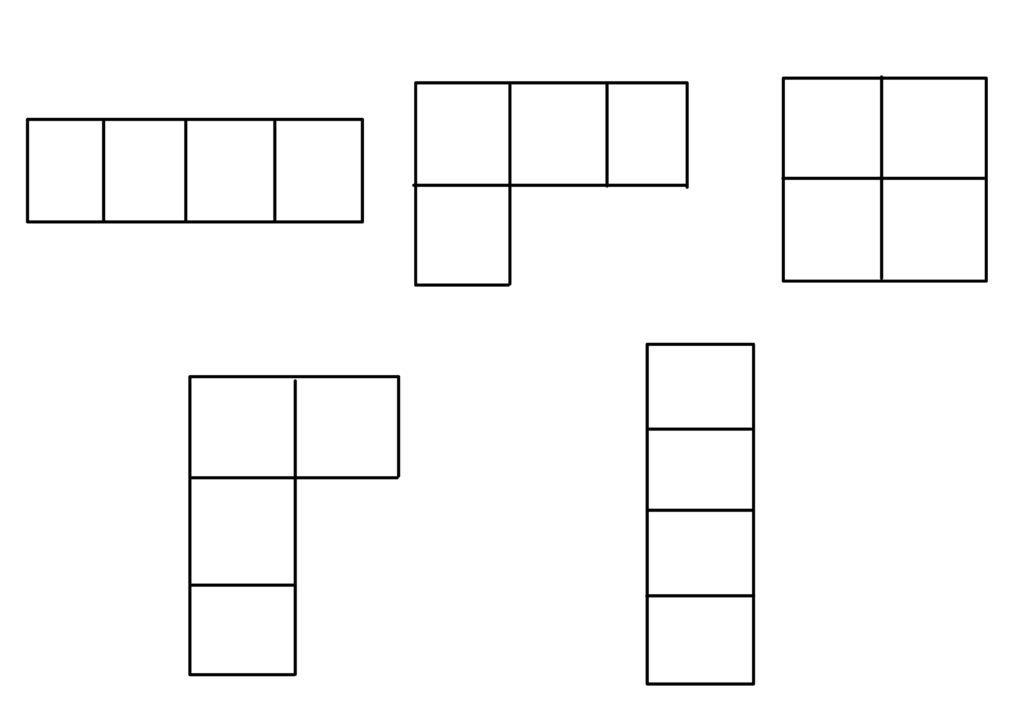
$n=4$ の場合のヤング図形は以下の5つです。

なぜこの図形が必要なんですか？

「どうしてヤング図形が必要なのか？」という疑問を持たれる方もいらっしゃると思いますので、それについて言及しておきます。

本日から数回に渡って解説する対称群の共役類に関係してくるからです。
より具体的には

対称群の共役類が置換の型、あるいはヤング図形で定まる。

のです。
本日から数回は、これを示すことが目標です。

皆様のコメントを下さい！

今回はディリクレです。

ディリクレ(Dirichlet, Peter Gustav;1805–1859)はドイツの数学者。
ガウスの整数論に強い影響を受け、ガウスの「整数論」を持ってフランスに渡り、フーリエ、ルジャンドルと知り合います。
フーリエ級数の研究に関連して、関数概念を明確にしたことで有名(それまでは関数は何らかの「式」で表されるものとしていました)です。
さらに解析的手法を整数論に持ちこむことにより、素数が自然数の集合の中でどのように分布するかを調べ、多くの結果を得ました。
1828年にベルリン大学教授、1855年にはガウスの後を継いでゲッチンゲン大学の教授となりました。

結

今回は、対称群の共役類の準備として、対称群の復習とヤング図形について解説しました。
ヤング図形は、置換の型を表した図形のことを指します。
なぜこのような図形を導入したのかと言うと、対称群お共益類が置換の方、あるいはヤング図形で定まるため、それを示したいからです。

次回は共益であることと置換の型が等しいことが同値であることを示します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34