「位数とは？」「剰余類とは？」「商群(剰余群)とは？」【代数学の基礎シリーズ】群論編その4

本記事の内容
同値関係と商集合の軽い復習
位数
1. 群の位数
2. 元(要素)の位数
部分群による同値関係と可換図式
左剰余類、右剰余類
1. 正規部分群であれば、左剰余類と右剰余類は一致します。
商群(剰余群)
商群がイマイチ分かりにくいんですが…
皆様のコメントを下さい！
結

本記事の内容

本記事は、商群(剰余群)について解説する記事です。

本記事を読むにあたり、同値関係と商集合について知っている必要があるため、以下の記事も合わせてご覧ください。

同値関係と商集合の軽い復習

同値関係と商集合を軽く復習します。

同値関係

同値関係

一般に、次の３条件を満たす集合

X

$X$ 上の関係

\sim

$\sim$ を同値関係(equivalence relation)という。

$x\in X$ のとき、 $x\sim x$ (反射律),
$x,y\in X$ のとき、 $x\sim y\Rightarrow y\sim x$ (対称律),
$x,y,z\in X$ のとき、 $x\sim y,\ y\sim z\Rightarrow x\sim z$ (推移律)

同値類

定理1.

x \in X

$x\in X$ と同値な要素全体を

C_{x}

$C_x$ と書き、これを

x

$x$ の同値類(equivalence class)という。すなわち、

C_{x} = {y \in X ∣ x \sim y}

$C_x=\{y\in X\mid x\sim y\}$ である。このとき、次が成り立つ。

$x\in C_x$ ,
$C_x\cap C_y\neq \emptyset \Rightarrow C_x=C_y$ ,
$C_x\neq C_y\Rightarrow C_x\cap C_y= \emptyset$ .

定理1.の証明は、【論理と集合シリーズ】その7を御覧ください。

商集合

商集合

\sim

$\sim$ を

X

$X$ 上の同値関係であるとする。各同値類は

X

$X$ の部分集合であるが、それらを要素とする集合を商集合(quotient set)とよび、

X / \sim

$X/\sim$ で表す。言い換えれば、同値類につけられた”名前”の集合が商集合である。

二項関係、同値関係、商集合について詳しくは【論理と集合シリーズ】その7を御覧ください。

位数

位数について解説します。
位数には2種類存在します。
それは

群の位数
要素の位数

です。
双方とも概念自体は難しいものではありませｎ。

群の位数

群の位数を一言で述べれば、

群の位数は、群の要素の数のこと。

です。
集合の言葉を使えば、群の位数とは群の濃度のことです。
記号で書けば、群 $G$ に対して、 $\left|G\right|$ が群 $G$ の位数です。

群の位数、有限群、無限群

群

G

$G$ に対してその要素の個数

| G |

$\left|G\right|$ を $G$ の位数(order)という。位数が有限な群のことを有限群という。有限群でない群、すなわち

G

$G$ の位数

| G |

$\left|G\right|$ が有限でない群

G

$G$ を無限群という。

元(要素)の位数

群の元(要素)の位数を一言で述べれば

最低何回演算して単位元となるのか？を表すその回数のこと。

です。
記号でかけば、演算が $\ast$ の群 $G$ の要素 $x\in G$ に対して $x^n\left(=x\ast x\ast \cdots\ast x\right)=1_G$ となるような自然数の内、最小のもの、ということになります。

元(要素)の位数

G

$G$ を群、

x \in G

$x\in G$ とする。もし、

x^{n} = 1_{G}

$x^n=1_G$ となるような正の整数が存在すれば、その中で最小のものを $x$ の位数という。もし、

x^{n} = 1_{G}

$x^n=1_G$ となる正の整数が存在しなければ、 $x$ の位数は $\infty$ である、あるいは $x$ は無限位数であるという。

例1.
$G$ が群であれば、その単位元の位数は $1$ です。
逆に $x\in G$ の位数が $1$ であれば、 $x=x^1=1_G$ となり $x=1_G$ です。
従って、単位元は位数が1のただ一つの元です。

例2.
$\mathbb{Z}$ は整数のたし算を演算としてで群でした。
$x\in\mathbb{Z}$ でかつ $x\neq0$ だとします。
このとき
$x^n=x\ast x\ast\cdots\ast x=x+x+\cdots+x=nx$
ですが、 $n\neq0$ のときに $nx\neq0$ ですので、 $x\neq0$ の位数は $\infty$ です。

有限群の元の位数は有限です。

定理2.

$G$ が有限群ならば、

$G$ の任意の元の位数は有限である。

定理2.

$g\in G$ ならば、 $G$ の元の個数が有限なので、 $\left\{1_G,\ g,\ g^2,\dots\right\}$ は有限集合です。
従って、ある自然数 $i<j$ が存在して、 $g^i=g^j$ です(このような議論を「部屋割り論法」と言ったりします)。
すると、 $g^{j-i}=1_G$ となります。
$j-i>0$ なので、 $g$ の位数は有限です。

定理2.の証明終わり

部分群による同値関係と可換図式

では、本題に入ります。

群 $G$ に関係を定めます。

$G$ を群、 $H\subset G$ を部分群とします。
$x,y\in G$ に対して、 $x^{-1}y\in H$ であるときに $x$ と $y$ は関係があると定めます。
すなわち、群 $G$ の要素に対して、関係 $\sim$ を
$x\sim y\Longleftrightarrow x^{-1}y\in H$
で定めます。
このとき、 $G$ 上の関係 $\sim$ は同値関係です。

実際、

反射律

$x^{-1}x=1_G$

$H$

$G$

$1_G=1_H\in H$

$1_G\in H$

$x^{-1}x\in H$

$x\sim x$

対称律

$x,y\in G$

$x\sim y$

$x^{-1}y\in H$

定理3.(部分群であることの必要十分条件)

群

$G$ の部分集合

$H$ が

$G$ の部分群になるための必要十分条件は次の3つの条件が満たされることである。

$1_G\in H$ である。ただし、 $1_G$ は群 $G$ の単位元である。
$x,y\in H\Rightarrow xy\in H$ である。
$x\in H\Rightarrow x^{-1}\in H$ である。

定理3.

【代数学の基礎シリーズ】群論編その2

定理3.

$a\in H$

$a^{-1}\in H$

$\left(x^{-1}y \right)^{-1}\in H$

$\left( x^{-1}y\right)^{-1}=y^{-1}\left(x^{-1} \right)^{-1}=y^{-1}x$

$y^{-1}x\in H$

$y\sim x$

推移律

$x,y,z\in H$

$x\sim y$

$y\sim z$

$x^{-1}y\in H$

$y^{-1}z\in H$

$x^{-1}z=x1_gz=x^{-1}yy^{-1}z$

$H$

$G$

定理3.

$a,b\in H$

$ab\in H$

$x^{-1}y\in H$

$y^{-1}z\in H$

$x1_gz=x^{-1}yy^{-1}z\in H$

$x1_gz=x^{-1}yy^{-1}z=x^{-1}$

$x^{-1}z\in H$

$x\sim y$

$y\sim z$

$x\sim z$

以上をまとめれば、次です。

命題4.

$G$ を群、

$H\subset G$ を部分群とする。群

$G$ の任意の要素

$x,y\in G$ に対して、関係

$\sim$ を

$x\sim y\Longleftrightarrow x^{-1}y\in H$ で定める。このとき、

$G$ 上の関係

$\sim$ は同値関係である。

もう一回商集合について。

同値類、商集合(quotient set)

$\sim$ を集合

$X$ 上の同値関係とする。

同値類

$x\in X$

$C(x)=\left\{y\in X\middle| x\sim y\right\}$

$x\in X$

同値類

商集合

$X$

$C(x)\ (x\in X)$

$X/{\sim}$

同値関係による商

商集合

自然な写像

$x\in X$

$\varphi(x)=C(x)\in X/{\sim}$

$\varphi:X\longrightarrow X/{\sim}$

$X$ から $X/{\sim}$ への自然な写像

代表元

$C\in X/{\sim}$

$C$

$x\in C$

$X$

$C$

代表元

完全代表系

$R\subset X$

$X/{\sim}$

$R$

$\sim$

完全代表系

可換図式

$f:A\longrightarrow B$ に対して、 $f(x)=f(y)$ であるときに $x\sim y$ だとします。
すなわち、集合 $A$ 上に、関係 $\sim$ を
$x\sim y\Longleftrightarrow f(x)=f(y)$
で定めます。
このとき、関係 $\sim$ は同値関係です。

実際、以下が成り立ちます。

反射律
$x\in A$ に対して、 $f(x)=f(x)$ により $x\sim x$ です。
対称律
$x,y\in A$ に対して、 $x\sim y$ 、すなわち $f(x)=f(y)$ とします。
このとき、 $f(y)=f(x)$ だから、 $y\sim x$ です。
推移律
任意の $x,y,z\in A$ に対して、 $x\sim y$ かつ $y\sim z$ 、すなわち $f(x)=f(y)$ かつ $f(y)=f(z)$ だとすると、 $f(x)=f(z)$ により $x\sim z$ です。

このとき、同値関係 $\sim$ による商集合 $A/{sim}$ から $B$ への写像 $\bar{f}:A/{\sim}\longrightarrow B$ を $C=C(x)\in /{\sim}\ (x\in A)$ に対して $\bar{f}(C)=f(x)$ と定めます。

このとき、 $x,y\in A$ で $C(x)=C(y)$ ならば、 $y\in C(x)$ となり、 $y\sim x$ なので、同値関係の定め方から $f(x)=f(y)$ です。
従って、写像 $\bar{f}:A/{\sim}\longrightarrow B$ は写像としての体裁が整っています(定義域の同じ要素が終域の同じ要素と対応している、という意味で、これを満たすような写像をwell-definedな写像といいます)。
$\bar{f}$ の定め方から、 $\pi:A\longrightarrow A/{\sim}$ を自然な写像とすると、 $f=\bar{f}\circ \pi$ です。

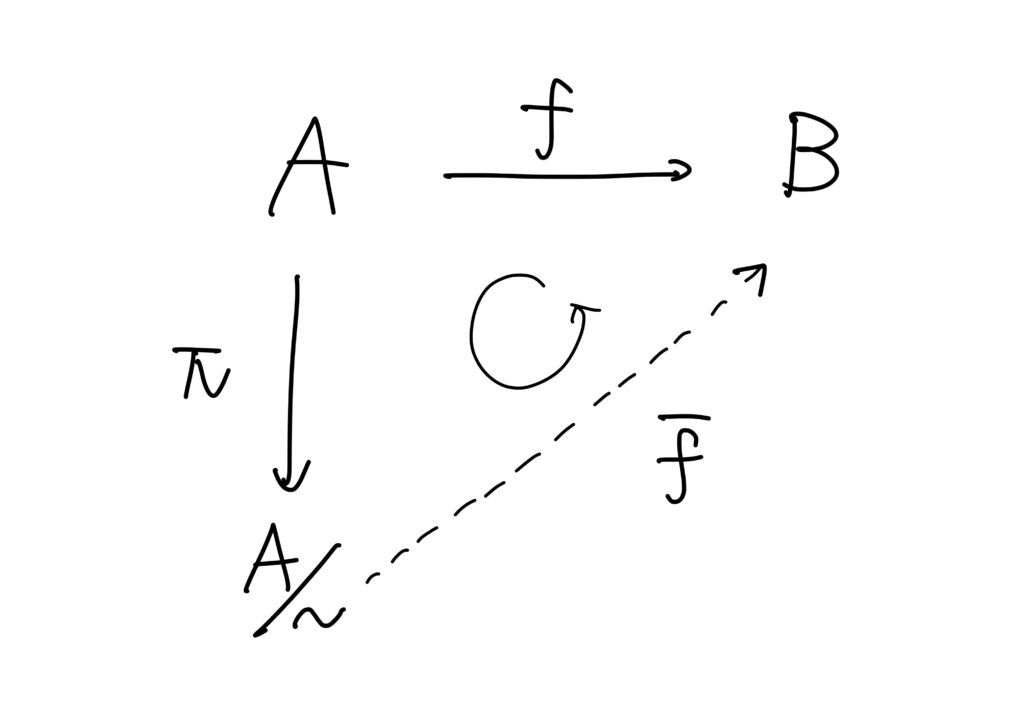
一般に、上手のように複数の写像があるずで、同じ集合の間の異なった経路の写像の合成が等しくなるとき、図は可換図式である、といいます。
この意味で、上手は可換図式です。
また、 $\sim$ の定め方から、 $x,y$ で $f(x)=f(y)$ ならば、 $x\sim y$ です。
故に $\bar{f}$ は単射であり、 $\bar{f}$ は $A/{\sim}$ から $f(A)$ への全単射写像です。

左剰余類、右剰余類

次に、左剰余類、右剰余類について解説します。

まず、それぞれが何か、ということを述べてしまいます。

左剰余類、右剰余類

$H\subset G$ を群

$G$ の部分群、

$x,y\in G$ とする。

左剰余類

$G$

$\sim_1$

$x\sim_1 y\Longleftrightarrow x^{-1}y\in H$

$\sim_1$

$x\in G$

$xH$

$x\in H$

$H$

左剰余類

$G/{\sim_1}$

$G/{H}$

右剰余類

$G$

$\sim_2$

$x\sim_2 y\Longleftrightarrow yx^{-1}\in H$

$\sim_2$

$x\in G$

$Hx$

$x\in H$

$H$

右剰余類

$G/{\sim_2}$

$H\backslash{G}$

$G$ が可換群であれば、左剰余類と右剰余類は一致します。
どうして左剰余類と右剰余類と分かれているか、というと群は必ずしも可換ではないからです。

例5. $G=\mathbb{Z}$ 、 $H=m\mathbb{Z}=\left\{mn\middle|n\in\mathbb{Z}\right\}$ とします。
このとき、
$a\sim b\Longleftrightarrow (\exists k\in\mathbb{Z})\ {\rm s.t.}\ b=a+mk$
で $\mathbb{Z}$ 上の関係 $\sim$ を定めます。
また、
$(\exists k\in\mathbb{Z})\ {\rm s.t.}\ b=a+mk$
のとき、 $a\equiv b\ ({\rm mod}\ m)$ と書きます。
このとき、 $a\in\mathbb{Z}$ の $H$ に関する剰余類は $a$ の合同類 $a+m\mathbb{Z}\left\{a+mk\middle| k\in\mathbb{Z}\right\}$ であり、左剰余類 $G/{H}=\mathbb{Z}/{m\mathbb{Z}}$ は、
$\mathbb{Z}/{m\mathbb{Z}}=\left\{\bar{0},\bar{1},\bar{2},\cdots,\overline{m-1}\right\}$
です。
ただし、 $k\in\left\{0,1,\dots,m-1\right\}$ に対して、 $\bar{k}$ は
$\bar{k}=\left\{l\in\mathbb{Z}\middle|l\equiv k\ ({\rm mod}\ m)\right\}$
を指します。
すなわち、 $\bar{k}$ は、 $m$ で割った余りが $k$ であるような整数の集合、ということです。

正規部分群であれば、左剰余類と右剰余類は一致します。

命題6.

$N$ が群

$G$ の正規部分群だとする。

$g\in G$ ならば、

$gN=Ng$ である。

命題6.の証明

$n\in N$ であれば、 $N$ は $N\triangleleft G$ だから( $N$ は $G$ の正規部分群だから) $n^\prime=gng^{-1}$ とおくと、 $n^\prime\in H$ です。
故に、 $gn=n^\prime g\in N_g$ です。
これが全ての $n\in N$ について成り立つので、 $gN\subset Ng$ です。
同様にして、 $Ng\subset gN$ も成り立つため、 $Ng=gN$ です。

命題6.の証明終わり

商群(剰余群)

ようやっと本題です。

先程説明した $G/{N}$ には、 $N$ が $G$ の正規部分群であるときに適切に演算を定めることで群となります。
これが商群(剰余群)です。

$G$ を群、 $N$ を $G$ の正規部分群とします。
また、 $\pi:G\longrightarrow G/{N}$ を自然な写像とします。
つまり、 $g\in G$ に対して、
$\pi(g)=gN\in G/{N}$
です。
$G/{N}$ の2つの要素を剰余類の代表元 $g,h$ により $gN$ 、 $hN$ で表したとします。
このとき、 $gN\in G/{N}$ と $hN\in V$ との間の、 $G/{N}$ 上の演算 $\ast$ を
$\left( gN\right)\ast \left(hN \right)=ghN$
で定めます。

$g,h$ は代表元ですが、演算 $\ast$ は代表元のとり方に依存しません。
実際、 $gN$ 、 $hN$ の任意の要素はそれぞれ $n,n^\prime\in N$ により $gn,hn^\prime$ と書けます。
すると、
$gnhn^\prime=ghh^{-1}nhn^\prime$
ですが、 $h^{-1}nh\in N$ なので、 $h^{-1}nhn^\prime\in N$ です。
故に、 $gnhn^\prime$ 、 $gh$ の剰余類は等しいです。

命題7.

$G$ を群、

$N\subset G$ を

$G$ の正規部分群とする。このとき

$G/{N}$ は、演算

$G/{N}\times G/{N}\ni \left( gN,hN\right)\mapsto ghN\in G/{N}$ によって群となる。

命題7.の証明

$1_GN=N$ は $G/{N}$ の単位元となります。
$ghk\in G$ であれば、 $G$ が群であることので結合律が成り立つから $(gh)k=g(hk)$ です。
故に、
$\begin{eqnarray} \left( \left( gN\right)\left( hN\right)\right)\left( kN\right)&=&\left( ghN\right)\left( kN\right)\\ &=&\left( (gh)k\right)N\\ &=&\left( g(hk)\right)N\\ &=&\left(gN \right)\left( (hk)N\right)\\ &=&\left( gN\right)\left( \left( hN\right)\left( kN\right)\right) \end{eqnarray}$
となるため、結合律が成り立ちます。

$\left( g^{-1}H\right)\left( gH\right)=g^{-1}gH=1_{G}H=gg^{-1}H=\left( gH\right)\left( g^{-1}H\right)$
となるので、逆元も存在します。

命題7.の証明終わり

この演算により $G/{H}$ は群となるので、 $G/{N}$ を商群(剰余群)といいます。

商群(剰余群)

$N$ を群

$G$ の正規部分群とする。左剰余類

$G/{N}$ は演算

$G/{N}\times G/{N}\ni \left( gN,hN\right)\mapsto ghN\in G/{N}$ により群となる。この

$G/{H}$ を

$G$ の

$N$ による商群(quotient group)または剰余群(factor group)と呼ぶ。

例8. $n>0$ を正の整数として、 $\mathbb{Z}/{n\mathbb{Z}}$ を考えます。
$x\in \mathbb{Z}$ の $n\mathbb{Z}$ に関する剰余類を $\bar{x}$ で書くことにします。
$x,y\in\mathbb{Z}$ に対して、 $x+y$ を $n$ で割った余りを $r$ とすると、 $\overline{x+y}=\bar{r}$ です。
$\mathbb{Z}/{n\mathbb{Z}}$ の演算は
$\bar{x}+\bar{y}=\bar{r}$
とすることで群となるので $\mathbb{Z}/{n\mathbb{Z}}$ は $\mathbb{Z}$ の $n\mathbb{Z}$ による商群です。

商群がイマイチ分かりにくいんですが…

筆者個人の意見ですが、商群は難しい概念だと思います。
本質的には商群が難しいと言うより、商の概念が難しいのだと思います。
筆者が学部、修士とお世話になった教授曰く

「商の概念を理解できるか否かで数学の理解度が大きく変わる。商の概念の理解は、ある種大学数学における登竜門的存在である。」

だそうです。
そこで、商群についてもう少し述べようと思います。

商群(剰余群)のモチベーションとしては

商集合

$G/{H}$ に群の構造を入れたい。

ということです。

$G/{H}$ の正体としては、とある同値関係の商集合です。
一般に群 $G$ の部分群があれば、群に同値関係を入れることができます。
どう定めるかと言うと、
$(\forall x,y\in G)\quad x\sim y\overset{\text{def}}{\Longleftrightarrow}x^{-1}y\in H$
と定めます(この関係 $\sim$ はたしかに同値関係になっていますが証明は省きます)。
$G/{H}$ はこの同値関係における商集合というわけです。

$G/{H}$ の要素は集合ですが、
$xH=\left\{xh\middle|h\in H\right\}$
という形をしています。
ちなみに、 $xh$ は $H\subset G$ ですので $x\in G$ と $h\in H$ に $G$ の演算を施したものです。

ここで注意なのが、

あくまで

$G/{H}$ は”現時点では”単なる集合に過ぎない。

ということです。
この単なる集合 $G/{H}$ に群の構造を入れたい、つまり群にしたいわけです。
では、同演算を定めるか、という話になりますが、以下で定めます。
$\left( \forall xH,\ yH\in G/{H}\right)\quad xH\ast yH=(xy)H\tag{#}$
「よし、これで群になるのか！」と思われるかもしれませんが、これでは実は $G/{H}$ は必ずしも群とはなりません。

例えば、 $G=\mathcal{S}_3$ 、すなわち $3$ 次の対称群とします。
ちなみに、 $3$ 次の対称群というのは、番号 $1,2,3$ の並び替え(写像)によりなる群です。
要素の個数は $3!=6$ 個です。

さて、
$H=\left\{{\rm id},\ (1\ 2)\right\}$
( ${\rm id$ は恒等写像)とすると、 $H$ は $G$ の部分群となります(簡単に確かめられます)。
このとき、 $G/{H}$ の要素は
$\begin{eqnarray} &&H=\left\{{\rm id},\ (1\ 2)\right\}=(1\ 2)H,\\ &&(1\ 2\ 3)H=\left\{(1\ 2\ 3),\ (1\ 3)\right\}=(1\ 3)H,\\ &&(1\ 3\ 2)H=\left\{(1\ 3\ 2),\ (2\ 3)\right\}=(2\ 3)H \end{eqnarray}$
と書くことができます。

では $(1\ 3)H\ast (2\ 3)H$ を $(#)$ に則って計算してみます。
$(1\ 3)H\ast (2\ 3)H=\left( (1\ 2)(2\ 3)\right)H=(1\ 2\ 3)H$
です。
先程述べた通り、 $(1\ 2\ 3)H=(1\ 3)H$ ですので、 $(1\ 2\ 3)H\ast (2\ 3)H=(1\ 2\ 3)H$ のはずです。
しかし計算してみると、
$(1\ 2\ 3)H\ast (2\ 3)H=\left( (1\ 2\ 3)(2\ 3)\right)H=(1\ 2)H$
となり、一致しません。
すなわち、この演算は要素の表示の仕方に依存している、ということになります。
$xH=xhH\ (h\in H)$ ですので、 $xH$ 表示の仕方は複数あります。
こういう状況の中で、 $(#)$ を演算として定めたいわけなのです。

$xH$ 、 $yH$ を $h,k\in H$ を用いてそれぞれ $(xh)H$ 、 $(yk)H$ と書いたとしましょう。
成り立ってほしいこととしては、
$(xh)H\ast (yk)H=(xy)H$
です。
$(xh)H\ast (yk)H$ を $(#)$ に則って計算すると、
$(xh)H\ast (yk)H=(xhyk)H$
です。
つまりは

$(xhyk)H=(xy)H$ が成り立ってほしい！

ということです。

実は、 $H$ が $G$ の正規部分群であるときにはうまくいく、つまりは上記のことが成り立つのです。
実際、
$\begin{eqnarray} (xhyk)H&=&\left( xyy^{-1}hyk\right)H\\ \end{eqnarray}$
と変形します。
$H$ は正規部分群なので、 $y^{-1}hy\in H$ で、さらに今 $k\in H$ ですから、
$l=y^{-1}hyk$
とすると $l\in H$ となるわけです。
故に、 $l\in H$ に対して $lH=H$ ですので
$\left( xyy^{-1}hyk\right)H=(xyl)H=(xy)H$
となります。

したがって、群 $G$ の部分群 $H$ が正規部分群であるときには、 $G_{H}$ は演算 $(#)$ で群となり、 $G/{H}$ を商群(または剰余群)と呼ぶ、ということなのです。

皆様のコメントを下さい！

今回はピタゴラスです。

ピタゴラス(紀元前581年頃-紀元前507頃)はイオニアのサモス島出身の哲学者であり数学者です。
彼がイタリア半島の南端の植民都市クロトンに開いた学園(正確には「彼岸的神秘的」宗教的集団)では、幾何学、算術(数論)、天文、音楽が主要科目でした。
この学園に属していた人々をピタゴラス学派といいます。
イオニア学派が無神論的(唯物論的)であったことと比較して、ピタゴラス学派が宗教的(観念論的)であったことは興味深いことです。

この学園では「万物は数である」という根本原理を掲げ、商業上の利益に関係する計算術を数の理論まで高めました。
しかし、ピタゴラス学派が政治的意志を持つに至って、反対派の陰謀により滅ぼされたと言われています。
なお，Mathematics(数学)の語源であるギリシャ語の「マテマ」(μαθημα)は「学ばれるべきもの」と翻訳され、それから派生した「マテマティコイ」(μαθηματικι)は「学問をする人」という意味となって、特にピタゴラス学派の人々を指していました。
数学と数学者を指すようになったのは、後のプラトンとアリストテレスの時代になってからです。

宗祖のピタゴラス自身が数学の研究にどれほど係わっていたかは定かではありませんが、ピタゴラス学派による幾何学への貢献は多大なものがありました。
三角形の内角和定理や三平方の定理の証明も、ピタゴラスもしくは彼の学派に属する数学者に依るものです。
このため、三平方の定理はピタゴラスの定理ともよばれます。
紀元後3世紀にディオゲネス・ラエルティオス(Diog ́enes La ́ertios;哲学史家。生没年は不明)により書かれた『ギリシャ哲学者列伝』(Vitae Philosophorum)の第8巻第1章には、数学者アポロドロス(Apollodorus;生没年は一切不明)の証言としてピタゴラスが三平方の定理を発見したことが書かれていますが、ピタゴラス自身は、直角二等辺三角形の場合のみ証明を持っていたと考えられています。
また、ピタゴラスはバビロニアに滞在していたことがあり、そのときに三平方の定理(少なくとも結果だけ)を学んだという説もあります。

いかがでしたか？
よく知られているピタゴラスの定理に名を残す数学者(またはその集団)です。
ここに書かれている事のほかにでピタゴラスについてご存知のことがあれば是非コメントで教えて下さい！

結

今回は位数、剰余類、商群について解説しました。
位数とは、群の要素の数と、何回演算すると単位元に戻るのかという数、剰余類は剰余を集めた集合で、それに適切な演算を定めることで群となり、それを商群と呼びます。

次回は準同型定理(第一同型定理)について解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

代数についてより詳しく知りたい方は以下を参考にすると良いと思います！

コメントをする

名前:名無しさん : 投稿日：2023/02/16(木) 14:03:03 ID：MzODMzOTM

完全代表系の定義において、R⊂S/~としていますが、R⊂Sではないのでしょうか？
また、商群はNが正規部分群でない場合も定義できるのですか？

返信

名前:オノコウスケ : 投稿日：2023/02/19(日) 03:05:59 ID：Y1MDQ3MDI

名無し様

>完全代表系の定義において、R⊂S/~としていますが、R⊂Sではないのでしょうか？
ご指摘ありがとうございます。
おっしゃるとおりでした。訂正いたしました。

>また、商群はNが正規部分群でない場合も定義できるのですか？
ご指摘ありがとうございます。
商集合 $G/{N}$ が群たりえる(つまり商群となる)のは $N$ が $G$ の正規部分群のときです。
補足を加筆いたしました。

返信

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

本記事の内容

同値関係と商集合の軽い復習

同値関係

同値類

商集合

位数

群の位数

元(要素)の位数

定理2.

定理2.の証明終わり

部分群による同値関係と可換図式

群GGに関係を定めます。

もう一回商集合について。

可換図式

左剰余類、右剰余類

正規部分群であれば、左剰余類と右剰余類は一致します。

命題6.の証明

命題6.の証明終わり

商群(剰余群)

命題7.の証明

命題7.の証明終わり

商群がイマイチ分かりにくいんですが…

皆様のコメントを下さい！

結

コメントをする

群 $G$ に関係を定めます。