本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
※「これを5分で解けるかな!?」も是非挑戦してみて下さい!
前回の問題については以下の記事を御覧ください!
今日の問題
1から6までの自然数\(\left\{ 1,2,3,4,5,6\right\}\)を考え、その中から隣り合う数を含まないようにして何個かの数を選び出します。すると、1個選ぶときは
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p29.
$$
\left\{ 1\right\},\ \left\{ 2\right\},\ \left\{ 3\right\},\ \left\{ 4\right\},\ \left\{5\right\},\ \left\{ 6\right\}
$$
の6通り、2個選ぶときは
\begin{eqnarray}
&&\left\{ 1,3\right\},\ \left\{ 1,4\right\},\ \left\{ 1,5\right\},\ \left\{ 1,6\right\},\ \left\{ 2,4\right\},\\
&&\left\{ 2,5\right\},\ \left\{ 2,6\right\},\ \left\{ 3,5\right\},\ \left\{ 3,6\right\},\ \left\{ 4,6\right\}
\end{eqnarray}
の10通り、3個選ぶときは、
$$
\left\{ 1,3,5\right\},\ \left\{ 1,3,6\right\},\ \left\{ 1,4,6\right\},\ \left\{ 2,4,6\right\},\
$$
の4通りとなります。
これと同じ方法で、1から10までの10個の自然数を考えると、1個、2個、3個、4個、5個の数を選び出す仕方はそれぞれ何通りあるでしょうか。また、一般の1から\(n\)までの自然数を考えるときはどうでしょうか。
チャレンジの結果…
チャレンジの結果…解けました。
解けましたが、「結構簡単だな…」という印象で、解答がエレガントか?というと少々疑問が残る感じでした。
筆者の解答
正直なところ、解くということ自体1時間もかかりませんでした。
ただ、おそらく正攻法による解答だと思いますので、エレガントなのか?と言われると少々疑問です。
さて、では筆者の解答を紹介します。
①1個取り出すとき
これは単純で、\({}_{10}C_{1}=10\)通りです。
②2個取り出すとき
真正直にやってみると、

だから、
$$
{}_8C_{1}+{}_7C_{1}+\cdots+{}_1C_{1}+0+0=36
$$
により、答えは36個です。
③3個取り出すとき
ここで、真正直に解くやり方もあるのでしょうが、面倒そうなので、考え方を変えてみました。
結局のところ、条件はあれど10個の数値から3つの数値を取り出す組み合わせのパターンを求めよ、というのが今回の問題です。
その条件は、「隣り合う数値は同時に取り出すことができない」というものでした。
ということは、7個のボールを並べたとき、残りの3つのボールが入るパターン数と同じだと気づきました。
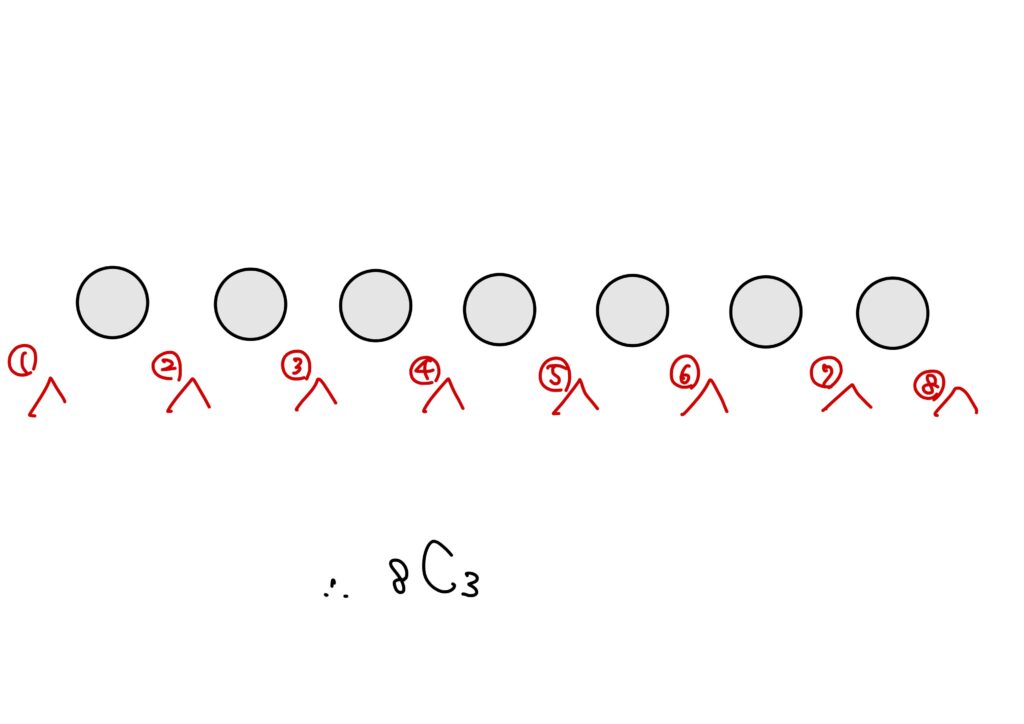
ボールと数値の対応は、単純に計10個の玉に数字を左から順々に当てはめていけばボールと数値が一意に対応するのでOKです。
となれば、話は簡単で、7個の玉の間は計8つあり、そこから3つ選ぶわけですので、
$$
{}_8C_{3}=56
$$
により、56通りです。
同様にすれば、4個取り出すとき、5個取り出すときのパターン数がわかります。
④一般化してみる
一般化してみる、といっても簡単です。
要するに、\(n\)個のボールから、隣り合わないように\(k\)個のボールを選ぶときは、次のようになります。
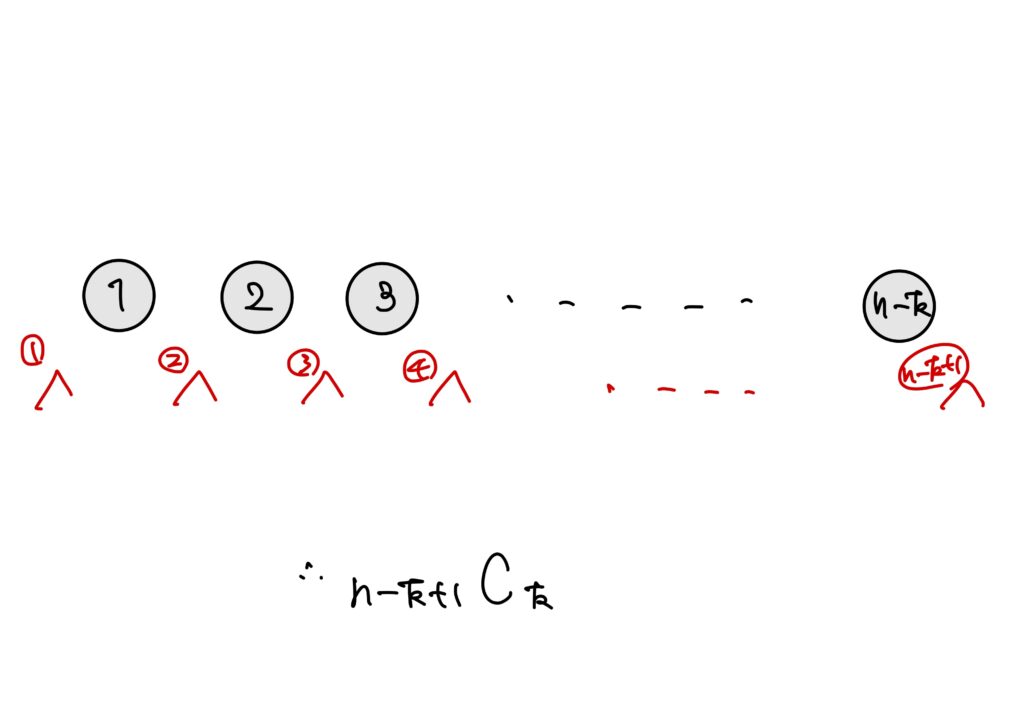
故に、
$$
{}_{n-k+1}C_{k}
$$
通りとなります。
投稿されたエレガントな解答
(前略)
さて、この問題を解くだけならば簡単です。\(1\)から\(n\)までの\(n\)個の自然数から\(k\)個を抜き出し、その中のどの2数も隣り合わない抜き出し方を\(f(n,k)\)通りとします。すると、それぞれの抜き出し方は、次の並べ方と1対1対応します。\(n-k\)個の白玉を横1列に並べ、その間に\(k\)個のくろたまをつぎの規則で挿入して、\(n\)個の偶にした並べ方です。その規則とは、左端や右端に黒玉を置いてもよいが、2個以上の黒玉を隣り合わせに置かないというものです。この並べ方のそれぞれに対して、左端から右端までの\(n\)個の玉に順番に\(1,2,3,\cdots,n\)と番号をつけ、くろたまにつけた番号だけを抜き出すと、これらの番号は出題の条件を満たしています。ところが、くろたまの入れ方は簡単です。白玉の間にある\(n-k+1\)個の隙き間から\(k\)個の隙き間を選び出し、そこへ黒玉を1個ずつ入れればよいからです。\(n-k+1\)個のものから\(k\)個を選び出す組み合わせの仕方なので、
$$
f(n,k)={}_{n-k+1}C_{k}\tag{1}
$$
が得られます。こうして、\(n=10\)のときは、
$$
{}_{10}C_{1}=10,\quad {}_{9}C_{2}=36,\quad {}_{8}C_{3}=56,\quad {}_{7}C_{4}=35,\quad {}_{6}C_{5}=6
$$
となります。これより少し複雑な解法として、\(f(n,k)\)通りの抜き出し方を、\(n\)を含むものと含まないものに分ける方法があります。\(n\)を含むときは、その他の数は\(n-2\)以下なので、その抜き出し方は\(f(n-2,k-1\)通りです。また、\(n\)を含まないときは、\(n-1\)以下の自然数に対する抜き出し方となるので、\(f(n-1,k)\)通りです。こうして、
$$
f(n,k)=f(n-2,k-1)+f(n-1,k)\tag{2}
$$
となりますが、
\begin{eqnarray}
&&f(n,1)=n\\
&&f(n,2)=1+2+3+\cdots+(n-2)\tag{3}
\end{eqnarray}
はほとんど明らかなので、式(1)が得られます。なお、式(3)はつぎの解答で説明します。さらにもう少し複雑な解法として、\(f(n,k)\)通りの抜き出し方を、それに含まれる最大の自然数で分類する方法があります。この数が\(m\)ならば、その他の数は\(m-2\)以下なので、その抜き出し方は\(f(m-2,k-1)\)とおりです。こうして、
\begin{eqnarray}
f(n,k)=f(n-2,k-1)&+&f(n-3,k-1)\\
&+&\cdots+f(2k-3,k-1)\tag{4}
\end{eqnarray}
となります。
なお、式(4)に\(k=2\)を代入すると、式(3)が得られます。つぎに、この問題の一般化に移ります。ごく自然な一般化は、隣り合う数だけでなく、その1個隣りの数、2個隣りの数と、一般に\(d\)個隣りの数まで含めないとするものです。このときの解答は、式(1)を導いたときと同じ方法で、\({}_{n-d(k-1)}C_{k}\)通りとなります。すると、最初の問題の解答は、\(d=1\)としたものです。また、\(1\)から\(n\)までの数を巡回させると、\(1\)と\(n\)も隣り合うことになり、これも同時には含めないことになります。このときの解答は、\(\left[ {}_{n-k+1}C_{k}-{}_{n-k-1}C_{k-2}\right]\)通りとなります。
最後に、なんkの数を抜き出すかは問題とせず、とにかく隣り合う2数を含まない抜き出し方を考えます。これは、式で示せば
$$
f(n,1)+f(n,2)+\cdots+f(n,s)
$$
です。ここに、\(s\)は\(n\)が偶数ならば\(n/2\)、奇数ならば\((n+2)/2\)として、\(f(n,2)\)が\(0\)にならないところまでを加えます。これに1個も抜き出さない(つまり空集合を抜き出す)ときを便宜的に
$$
f(n,0)=1
$$
で与え、\(f(n)\)を
$$
f(n)=f(n,0)+f(n,1)+f(n,2)+\cdots+f(n,s)\tag{5}
$$
で定義します。すると、
$$
f(0)=1,\quad f(1)=2
$$
は明らかで、また、一般の\(f(n)\)にたいしては、抜き出した数に\(n\)が含まれていなければ\(f(n-1)\)通り、\(n\)が含まれていれば\(f(n-2)\)通りとなるので、
$$
f(n)=f(n-1)+f(n-2),\quad n\geq2
$$
も成り立ちます。これは\(f(n)\)が\(n+1\)番目の父母ナッチ\(\)であることを示すもので、この問題はフィボナッチ数を二項係数の和に分解する問題でもあったのです。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p251-p253.
なんと…フィボナッチ数と関連があるとは…全く気が付きませんでした。
!次回予告!
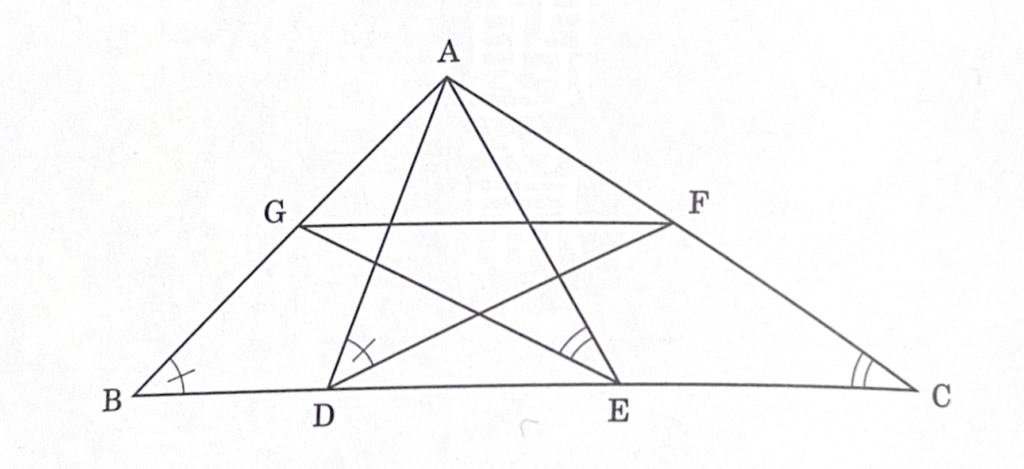
\(\triangle ABC\)において\(\angle BAC>90^\circ\)とする。辺\(BC\)上に点\(D,E\)を
$$
\angle BAE=\angle CAD=180^\circ-\angle BAC
$$
であるようにとり、辺\(AC,AB\)上にそれぞれ点\(F,G\)を
$$
\angle ADF=\angle ABC,\quad \angle AEG=\angle ACB
$$
であるようにとれば
$$
GF/\!/ BC,\quad DF=EG=FG
$$
であることを証明してください。『エレガントな解答をもとむ 名作セレクション2000~2020』数学セミナー編集部編、日本評論社、2022、p20.
筆者からの挑戦状!(5分で解けるかな?)
斜線部の面積を求めよ。ただし、全ての円の半径は\(2\)であり、それぞれが他の2円と1点で接しているものとする。
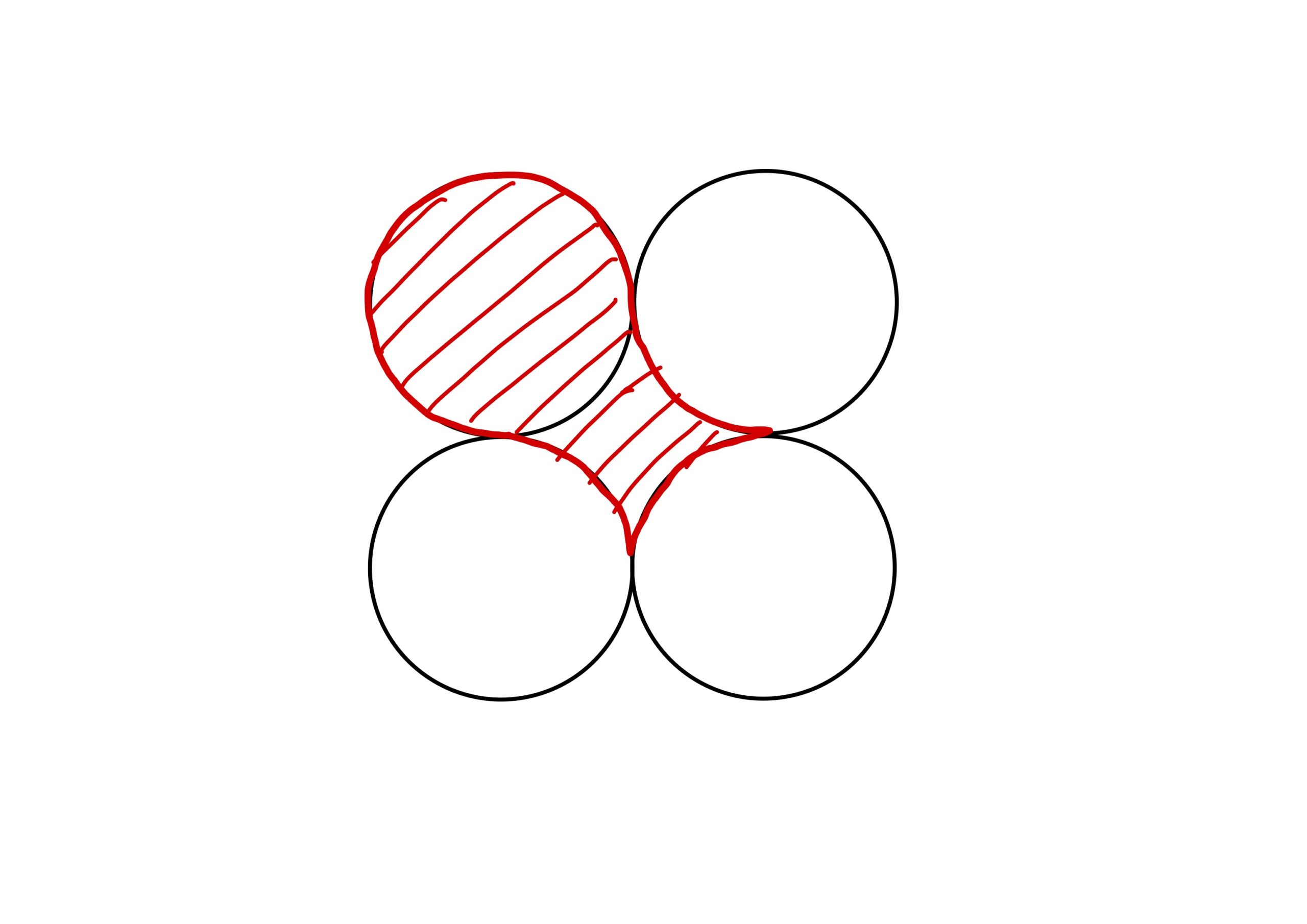
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「筆者からのの挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!




コメントをする