本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
平面上の円盤内から、一様な確率密度(ある領域から点が選ばれる確率はその領域の面積に比例すること)に従い、ランダムに選ばれた\(n\)個の点があるとします。この\(n\)個の点の凸包(この\(n\)個の点を含む最小の凸集合、すなわち\(n\)個の点のうちのいくつかを頂点とし、残りの点を内部に含む凸多角形)の内部に、この円盤の中心\(O\)が含まれる確率はいくらでしょうか。
できればこの問題の「平面」を「空間」に、「円盤」を「球」に換えてできる同様の問題についても確率を求めて下さい。さらに、一般次元にまで拡張した問題も考察してみて下さい。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p18.
いざ、チャレンジ
チャレンジの結果…一部解けました。
一般化した問題は解けませんでしたので、一部です。
筆者の解答
少々実験してみました。
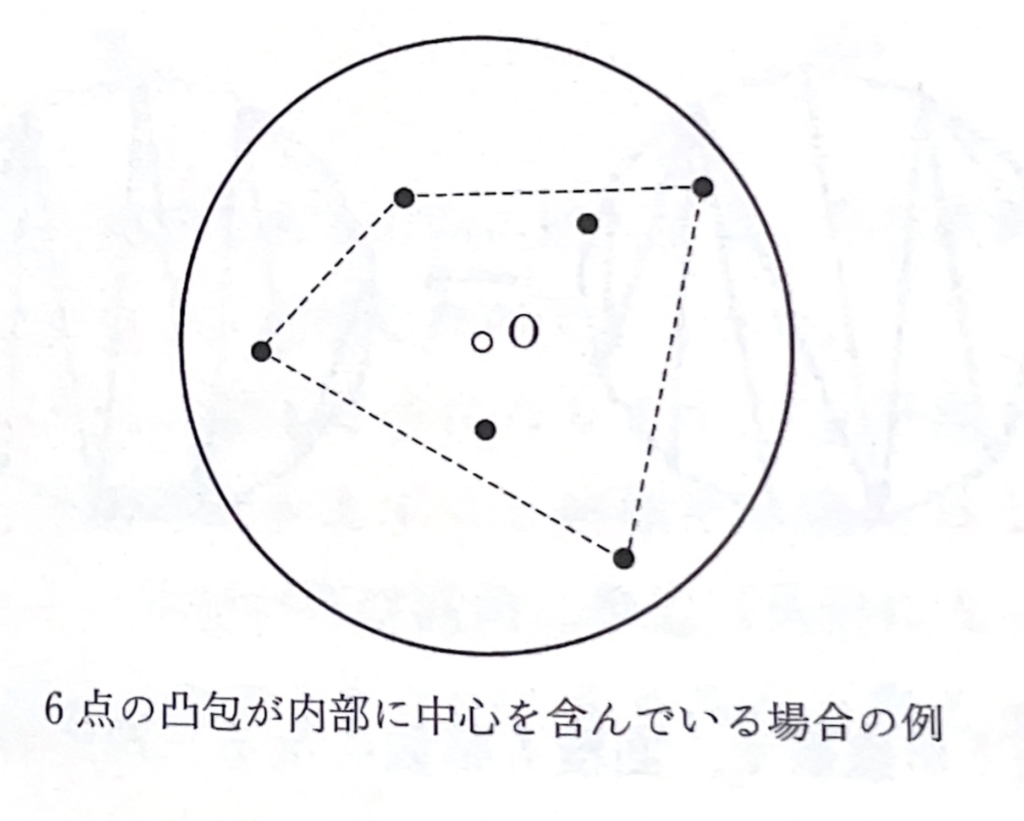
例えば、\(n=7\)のとき、以下のような状態になる確率を求めましょう、ということになります。

筆者の直感的には結構確率は高そうだな、と思ったので余事象を使うことにしました。
つまり、\(n\)個の点の凸包が点\(O\)を含まないような確率を求めることにしました。
ということは、「\(n\)個の点の凸包が\(O\)を含まない」ことの必要十分条件を求める必要があります。
再度実験です。

要するに、\(n\)個の点が端っこに寄ってれば良さそうです。
ただ、次のような場合はだめです。
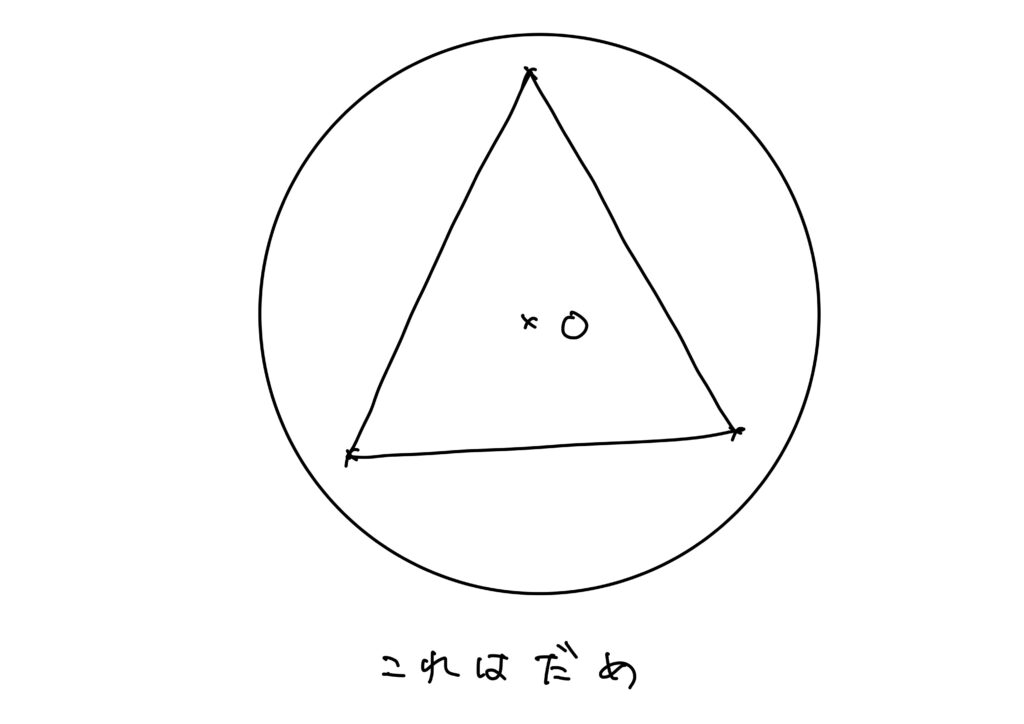
ということで、単に端っこに寄っているだけではだめで、\(n\)個の点が全てとある半円の中に入ってればよいのかな、と思いました。
つまり、「ある半円が存在して、その半円の中に\(n\)個の全ての点が含まれる」ということが必要十分条件なのでは?と思いました。
そこで、必要十分条件なのか考えてみました。
仮に、「ある半円が存在して、その半円の中に\(n\)個の全ての点が含まれる」とします。
また、その半円板にある\(n\)個の点で作る凸包の内部に円の中心\(O\)が含まれるとします(背理法)。
すると、円の直径上に点\(O\)が存在しないことになってしまい、矛盾です。
逆に、円盤内の任意の\(n\)個の点で作る凸包が\(O\)を含まないとすると、ある直径が存在してその直径上のどの点も凸包の内部に含まれません。
実際、どんな直径に対しても必ずそれ上の点が凸包の内部に含まれているとするとそこに\(O\)もまた含まれてしまいます。
したがって、必要十分条件が導けました。
あとは、確率を求めます。
どの確率かというと、「円の内部からランダムに選ばれた\(n\)点がある半円板上に含まれる確率」です。
これを\(p(n)\)と書きましょう。
ある直径に対して、\(n\)点がどちらか一方にある確率で存在するので、\(\displaystyle\left( \frac{1}{2}\right)^{n-1}\)であり、それが\(n\)パターン存在するわけですので、その\(n\)倍が\(p(n)\)です。
つまり、
$$p(n)=n2^{1-n}$$
です。
故に、求める確率は\(1-n2^{1-n}\)です。
投稿されたエレガントな解答
(前略)
まず、確率を求めるのですから、\(n\)の配置は一般の位置にある場合のみを考慮すればいいことになります。つまり、選ばれた点の中の3点、もしくは2点と中心\(O\)、が一直線上にあるなどという特殊な場合を考慮しても、確率の値には反映されないということです。なぜならそのようなことが起こる確率が\(0\)であるからです。ですから、以降の議論においては、いちいち断らなくてもこのような特殊な場合は除かれています。
(中略)
次に、「円盤\(D\)ないの\(n\)点の凸包が\(D\)の中心\(O\)を含まないための必要十分条件は、この\(n\)点がある半円板に含まれることである」が成立します。ここで半円板とは、\(D\)をある直径で半分に分けたものの一方のことです。\(n\)点がすべて半円板に含まれると、それらの凸包は中心\(O\)を含み得ないのは明らかですが、逆に中心\(O\)を含まない\(D\)内の凸集合はある直径で区切られた半円板に含まれることも、簡単な考察で判ります。
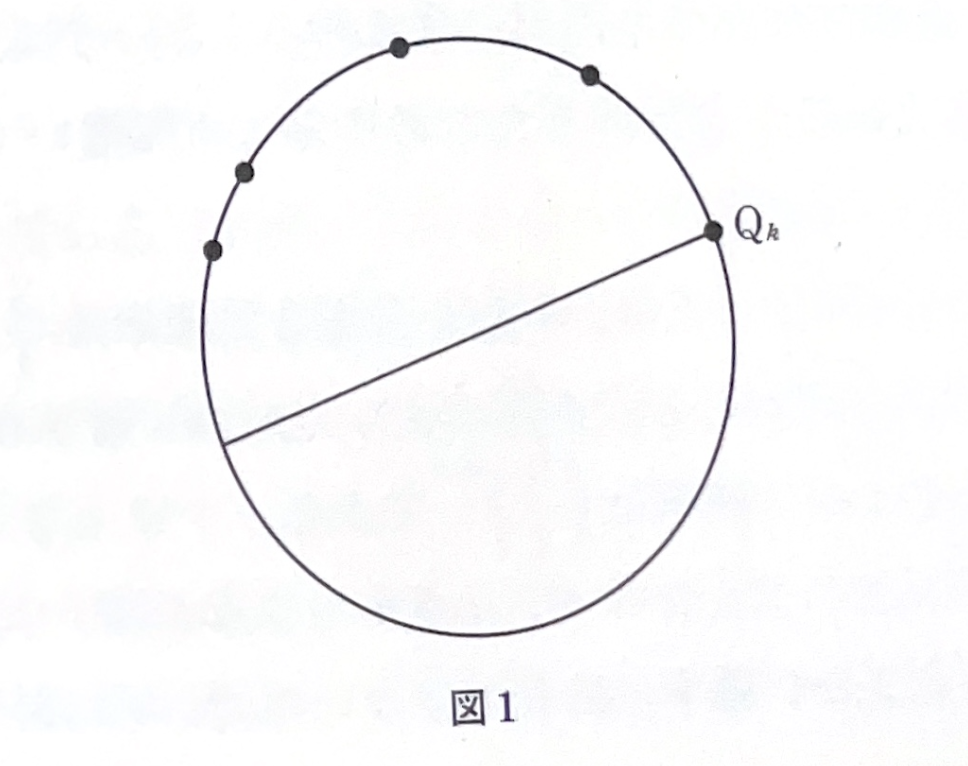
選ばれた\(n\)点を\(P_1,\cdots,P_n\)とし、\(P_i\)を通る半径が円盤の周囲にぶつかる点を\(Q_i\)とすると、\(Q_i,\cdots,Q_n\)は円周上から一様な確率分布によってランダムに選ばれた\(n\)点となります。したがって、「円周上からランダムに選ばれた\(n\)点\(Q_1,\cdots,Q_n\)」が、ある半円周上に含まれる確率」を\(f(n)\)とすると、\(1-f(n)\)が求める確率となります。(中略)
解法1:\(Q_1,\cdots,Q_n\)がある半円周上にあり、しかも\(Q_k\)がその半円周上反時計回りの順序で\(n\)点の中で最初のものであるような確率は、\(Q_k\)以外の\(n-1\)個の点が\(Q_k\)を反時計回りの視点とする半円周上にすべてのっている確率に等しいので、\(2^{1-n}\)となります。\(f(n)\)は、\(k=1,\cdots,n\)に関するこの非重複的な確率の和であるので、\(f(n)=n2^{1-n}\)となります。
(中略)
解法2:\(Q_1,\cdots,Q_{n-1}\)を含む最小の弧の中心の中心核がちょうど\(\theta\)となるような確率密度を考え、各\(\theta\)にたいし\(Q_1,\cdots,Q_n\)が半円周上にあるための\(Q_n\)の存在範囲を考察して\(n\)に関する漸化式を出し、確率を求める。
(中略)
解法3:円周の\(2m\)等分点からランダムに\(n\)点を選ぶとき、それが半円的である確率を求め、それの\(m\to\infty\)における極限値を求める。
解法4:\(Q_1,\cdots,Q_n\)で円周を切ってできる\(n\)個の弧の中心各を\(\theta_1,\cdots,\theta_n\)とすると、\(0<\theta_i<2\pi\ (i=1,\cdots,n)\)、\(\theta_1+\cdots+\theta_n=2\pi\)を満たす。この\(\theta_1,\cdots,\theta_n\)が成す空間を\(X\)とする。次に、\(\theta_i<\pi\ (i=2,\cdots,n)\)を満たすような点全体からなる\(X\)の部分集合を\(Y\)とする。求める確率は(\(Y\)の体積/\(X\)の体積)であるから、これを計算すれば良い。
(中略)
また、誤った解答として多かったのは、次のようなものです。
解法5(誤答):ある直径に対して、\(n\)点がどちらか一方にある確率でそんざいするから、\(f(n)=2^{1-n}\)である。
(中略)
解法6(誤答):\(n=3\)のとき、中心を含まない確率は\(\displaystyle\frac{3}{4}\)である。一般の\(n\)に関しては、\(n\)点から\(3\)点を選ぶ選び方が\({}_n \mathrm{C}_3\)通りあるので、\(n\)点の凸包が中心を含まない確率は\(\displaystyle\left( \frac{3}{4}\right)^{{}_n \mathrm{C}_3}\)である。
\(\displaystyle\frac{3}{4}\)という確率はあっていますが、\(n\)点から3点をかってに選んだときその凸包が中心を含まない確率は独立ではないので単純に掛けてはだめです。\(P_1,P_2,P_3\)の凸包と\(P_1,P_3,P_4\)の凸包とが中心を含まないとしたとき、\(P_1,P_2,P_4\)の凸包が中心を含まない確率は\(\displaystyle\frac{3}{4}\)ではないでしょう。ところで以上に挙げた解法はどれも、次元を高くした問題へ拡張するには困難があるよです。
(中略)
そこで、一般次元の球面に関する性質を調べて、高次元の問題の解法をさぐることにしましょう。\(d\)次元球は\(\left\{(x_1,\cdots,x_{d+1})\in\mathbb{R}^d\middle|x_1^2+\cdots+x_d^2\leq1\right\}\)であり、その表面を\(d-1\)次元球面といい\(S^{d-1}\)と書きます。つまり
$$
S^{d-1}=\left\{(x_1,\cdots,x_{d+1})\in\mathbb{R}^d\middle|x_1^2+\cdots+x_d^2=1\right\}
$$
で定義される\(d\)次元空間内の図形です。2次元球面が普通の球面であり、1次元球面は単位円周のことであり、9次元球面は数直線上の2点\(\left\{-1,1\right\}\)のことです。3次元以上の球面の定義できますが、それらの全体像は目で見ることはできません。想像をふくらませて心で見て下さい。
\(d-1\)次元球面\(S^{d-1}\)の中で、第\(d\)座標が0であるような点全体\(\left\{(x_1,\cdots,x_d)\in S^{d-1}\middle|x_d=0\right\}\)を\(S^{d-1}\)の赤道と言いますが、これは\(d-2\)次元球面と同じものなので、赤道球面と呼ぶこともあります。ですから、\(S^0\subset S^1\subset S^2\subset\cdots\subset S^{d-1}\subset\cdots\)とみなせます。また、原点を通る任意の\(d-1\)次元部分空間と\(S^{d-1}\)との交わりを大円と呼びますが、これも\(d-2\)次元球面です。ですから、大球面と呼ぶほうが的確かもしれません。
球面上の一点\(P\)に対し、球の中心に関して点対称な位置にある点を、\(P\)の対心点といい\(P^\ast\)と書きます。\(N=(0,\cdots,0,1)\)と\(S=(0,\cdots,0,-1)\)は互いに対心点ですが、これを\(d-1\)次元球面の北極と南極と呼びます。地球上の点が緯度と経度で表されるように、\(d-1\)次元球面上の北極と南極以外の点\((x_1,\cdots,x_d)\)はその点の最後の座標\(x_d\)と、その点から赤道への最短距離でおろしたところの点\((x_1,\cdots,x_{d-1},0)/\sqrt{1-x_d^2}\in S^{d-2}\)の二つで一意的に表すことができます。この\(d-1\)次元球面上の両極以外の転から赤道への対応を\(p_{d-1}:S^{d-1}\setminus\left\{N,S\right\}\to S^{d-2}\)と書きます。
\(d-1\)次元球面を一つの大円で切手できる2弧の成分の一つを\(d-1\)次元半球面と呼びます。\(d-1\)次元球面上の点集合は、ある\(d-1\)次元半球面に含まれるとき、半球面的と呼ぶことにします。
さて、我々の欲しいものは、「\(d\)次元球の表面である\(d-1\)次元球面からランダムに選ばれた\(n\)点\(Q_1,\cdots,Q_n\)が半球面的である確率」です。これを\(f(d,n)\)と書くことにしましょう。
\(Q_1,\cdots,Q_n\)が半球面的であるとき、\(Q_1\)が残りの点\(Q_2,\cdots,Q_n\)に関して外的である、内的であるというのを次で定義します。\(Q_1\)を含まず\(Q_2,\cdots,Q_n\)を含むような\(d\)次元半球面があるとき、\(Q_1\)は\(Q_2,\cdots,Q_n\)に関して外的であるといい、そうでないとき\(Q_1\)は\(Q_2,\cdots,Q_n\)に関して内的であると言うことにします。一般のいちで考える限り、\(Q_1\)が外的であることは\(Q_1\)を通るある大円で切ってできる半球面内に\(Q_2,\cdots,Q_n\)が含まれることである、ということに注意します。
さて、\(Q_1,\cdots,Q_n\)をランダムに選んだときそれらが半球面的でありしかも\(Q_1\)が\(Q_2,\cdots,Q_n\)に関して外的である確率を\(\alpha(d,n)\)、同様に内的である確率を\(\beta(d,n)\)と書くと、内的、外的は排反的ですから\(f(d,n)=\alpha(d,n)+\beta(d,n)\)となります。
\(Q_1\)を北極にするような座標を\(S^{d-1}\)上により、この座標に関しての赤道への対応\(p_{d-1}:S^{d-1}\setminus\left\{P,Q\right\}\to S^{d-2}\)による\(Q_2,\cdots,Q_n\)の像を考えると、\(Q_1\)が\(Q_2,\cdots,Q_n\)に関して外的である必要十分条件は、この像\(p_{d-1}\left( \left\{Q_2,\cdots,Q_n\right\}\right)\)が\(S^{d-2}\)内で半球面的であることになります。なぜなら、\(Q_1\)を通る大円で切ってできる半球面の\(p_{d-1}\)による像は赤道球面上の半球面であるからです。各店\(p_{d-1}(Q_i)\)は赤道球面上に一様な確率密度で分布しますから
$$
\alpha(d,n)=f(d-1,n-1)
$$
となります。
また、\(Q_1,\cdots,Q_n\)をランダムに選んだとき\(Q_2,\cdots,Q_n\)が半球面的であるが\(Q_1,\cdots,Q_n\)が半球面的でないお確率を\(\gamma(d,n)\)とおきます。\(Q_2,\cdots,Q_n\)が半球面的である確率は\(f(d,n-1)\)ですから、\(f(d,n-1)=f(d,n)+\gamma(d,n)\)、よって
$$
\gamma(d,n)=f(d,n-1)-f(d,n)
$$
となります。
次の考察がこの問題を解くための最大の鍵となります。\(Q_1,\cdots,Q_n\)が半球面的であるとき、\(Q_1\)が\(Q_2,\cdots,Q_n\)に関して内的であることと、\(Q^\ast_1,Q_2,\cdots,Q_n\)が半球面的でないことは同値と成るのです。なぜなら、\(Q_1\)を含まず\(Q_2,\cdots,Q_n\)を含む半球面は\(Q^\ast_1\)と\(Q_2,\cdots,Q_n\)を含むからです。よって、どのような半球面的な配置\(Q_2,\cdots,Q_n\)に対しても、\(Q_1\)が\(Q_2,\cdots,Q_n\)に関して内的となる\(Q_1\)の存在範囲と、\(Q_1,\cdots,Q_n\)が半球面的でない\(Q_1\)の存在範囲は、球の中心に関して対称であり、その面積(あるいは体積)は等しいので
$$
\beta(d,n)=\gamma(d,n)
$$
を得ます。
さて、\(f(d,n)=\alpha(d,n)+\beta(d,n)\)に以上のことを代入すると、\(f(d,n)=f(d-1,n-1)+f(d,n-1)-f(d,n)\)となり、これより漸化式
$$
f(d,n)=\frac{1}{2}\left( f(d,n-1)+f(d-1,n-1)\right)
$$
が得られます。
次にこの漸化式のための初期値について考察します。\(S^0=\left\{-1,1\right\}\)ですから、\(f(1,n)=2^{1-n}\)でありますが、このためには\(f(0,n)=0\)と定義すると良いことがわかります。また\(d\)弧以下の点の凸包は\(d-1\)次元以下の図形となり、それが球の中心を含む確率は\(0\)ですから、\(f(d,n)=1\ (d\geq n)\)となります。(中略)
では最後にこの漸化式を解いてみましょう。\(g(d,n)=2^{n-1}f(d,n)\)とおき、さらに\(g(d,n)\)の\(d\)に関する階差数列\(h(d,n)=g(d+1,n)-g(d,n)\)をとると、
\begin{eqnarray}
h(d,n)&=&h(d,n-1)+h(d-1,n-1)\\
h(0,n)&=&1,\quad h(d,n)=0\quad (d\geq n)
\end{eqnarray}
となります。
この漸化式と初期値はよく知られた二項係数のものなので
$$
h(d,n)={}_{n-1} \mathrm{C}_d=\frac{(n-1)!}{(n-1-d)!d!}
$$
となり、したがって
$$
f(d,n)=2^{1-n}\sum_{k=0}^{d-1}{}_{n-1} \mathrm{C}_k
$$
を得ます。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p140-p146.
読者の皆様への挑戦状!
空間の5点\(A,B,C,D,E\)に対して
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p18.
\begin{eqnarray}
&&AB=BC=CD=DE=EA,\\
&&AC=BD=CE=DA=EB
\end{eqnarray}
が成り立つとき、\(A,B,C,D,E\)は同一平面上にあるといえるでしょうか。
前回の問題は【1時間チャレンジシリーズ】挑戦⑳を御覧ください。
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする