本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
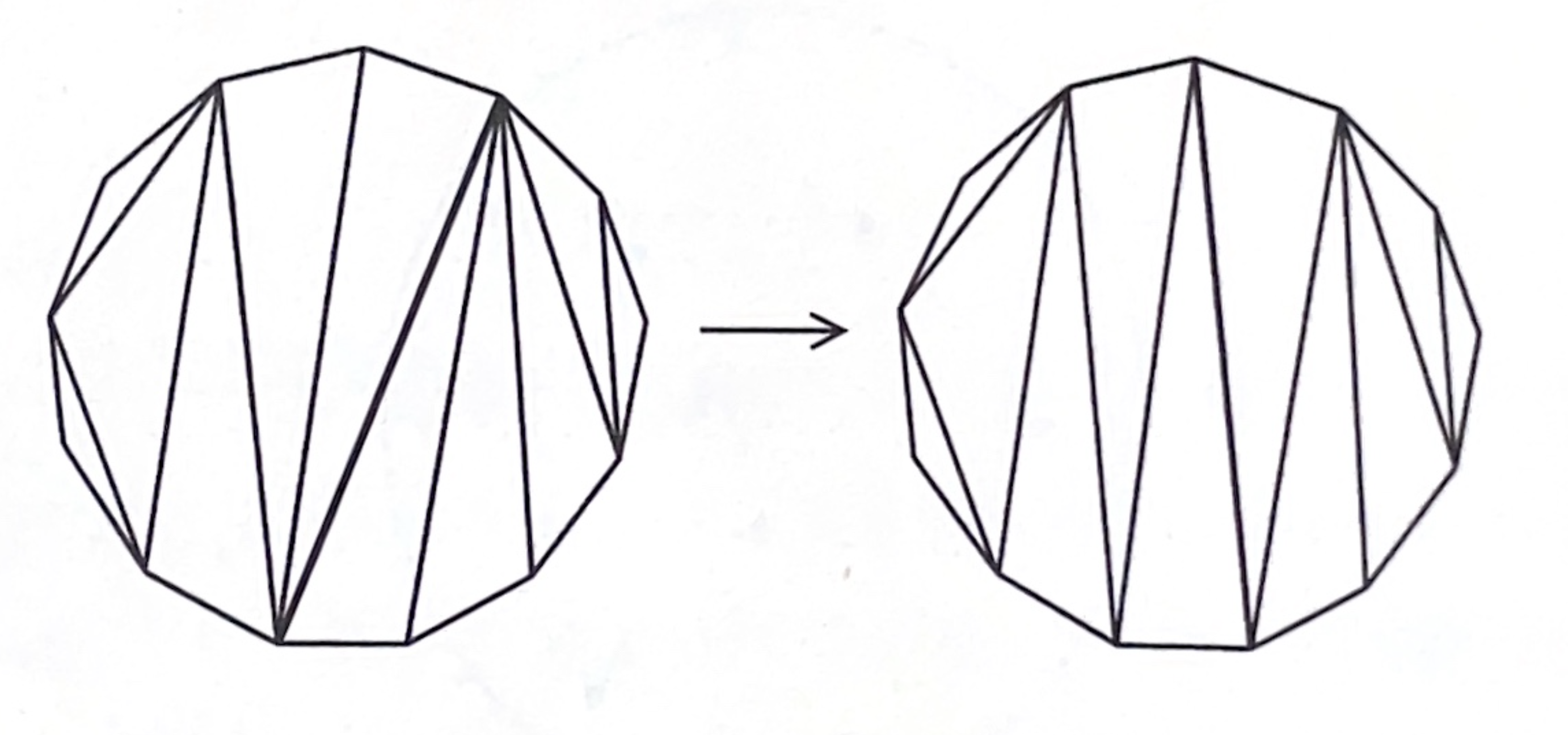
正十三角形に対角線を加えて三角形に分割した図形を考えます。下図のように、その作を対角変形と呼ぶことにします。どのように対角線を入れた2つの正十三角形も対角変形を繰り返すことにり、お互いに移り合います。どんな場合でも何回以下で移り合うでしょうか?
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p17.
いざ、チャレンジ
チャレンジの結果…解けませんでした…
ても足も出なかったというわけではありませんが、混乱してしまい、時間内に望ましい解答を与えることができませんでした。
筆者の解答
筆者の解答を紹介します。
ちょっとした疑問
まず、この問題を見たときに「回転は考慮するのか?」と疑問に思いました。
今回は正13角形に対する問題ですが、例えば簡単に正方形の場合を考えると、正方形を三角形に分割するように対角線を引けば次の2パターンが考えられます。
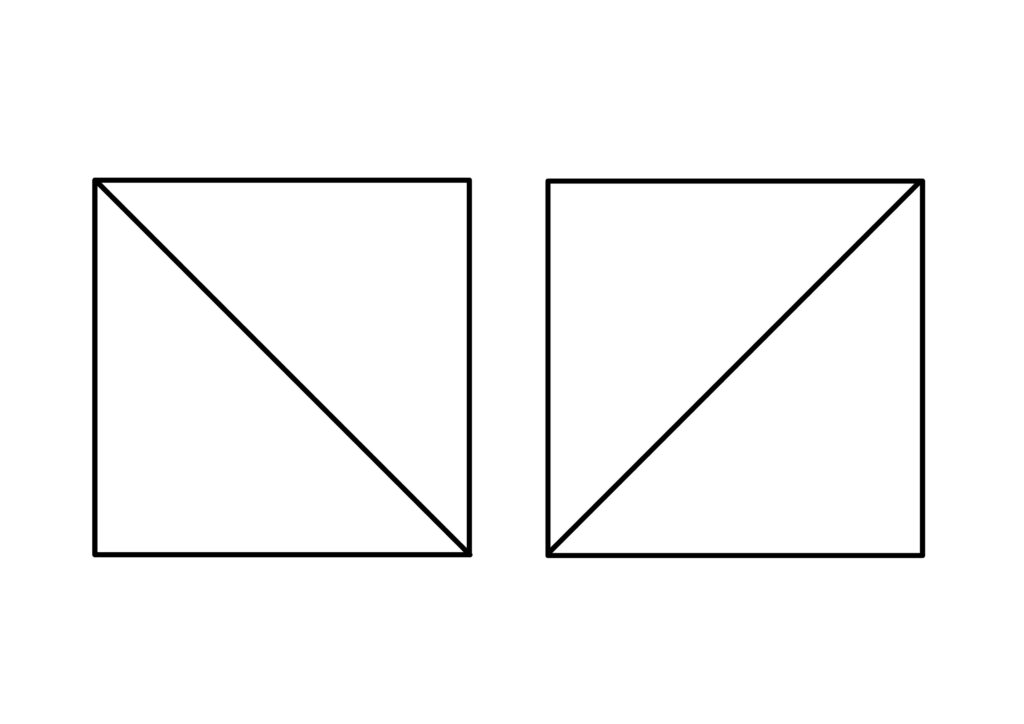
これらは\(90^\circ\)回転でもって互いに移り合います。
つまり、回転を考慮すれば対角変形なる操作を行わずとも、移り合わせることができます。
この場合はどう扱うのか?と思ったわけです。
とはいえ、回転については何も述べられていないので、回転は考慮しない、すなわち先の例でいうような図形同士は別物として扱うということにしました。
余談
「回転について何も述べられていないのだから、使ってもいいのでは?」と一瞬思いました。こういう場合、使っていいものでしょうか。
それとも使ってはいけないのでしょうか。
未だにわかりません。
ただ、おそらく出題者の意図とは異なるのだろうなという予想の元、使わないことにしました。
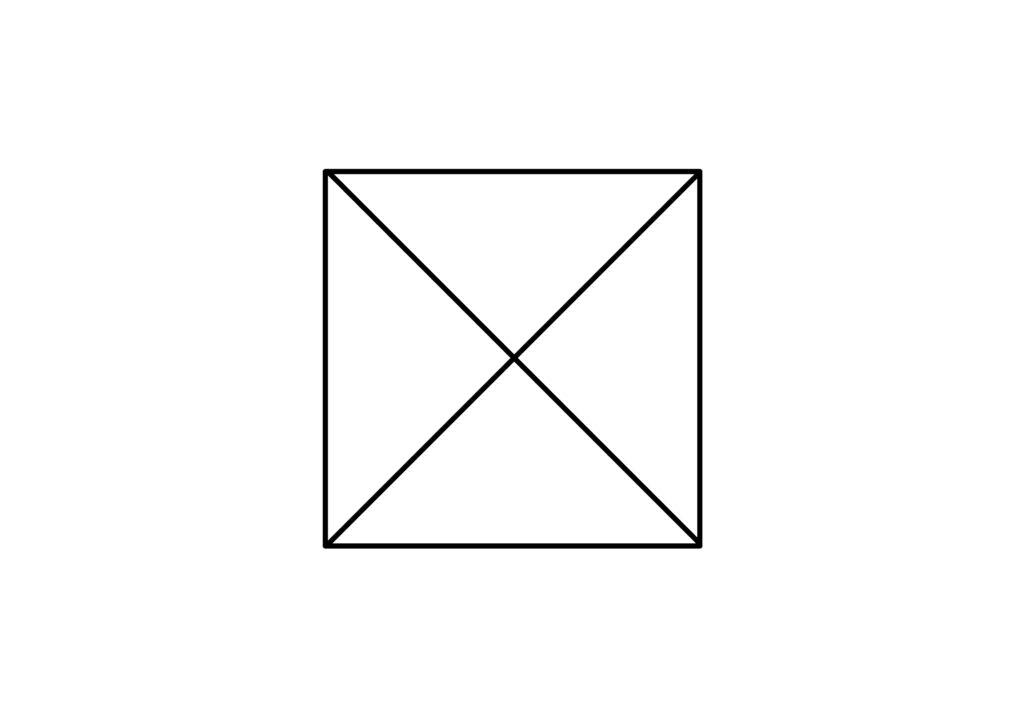
さらにいえば、問題を鵜呑みにして対角線を引けば
このように対角線を引いても正方形は三角形で分割されています。
おそらくこの場合、つまり対角線が交わっているような場合は除くのでしょうが、もしかしたら考えなければならないかもしれません。
簡単な実験をしてみました。
なぜ実験するかというと、もしかすると規則性があるかもしれないと思ったからです。
もし規則性が存在すれば、あとは数学的帰納法で証明して13角形の場合について考察すれば良いのです。
正方形の場合
先程紹介した正方形の場合について考えてみました。
先程の通り、正方形を三角形で分割するような対角線の引き方は2パターンしか存在しません。
そしてそれはお互い1回の対角変形で移り合います。
正五角形の場合
正五角形を三角形で分割するような対角線の引き方は大きく分けて以下の通りです。
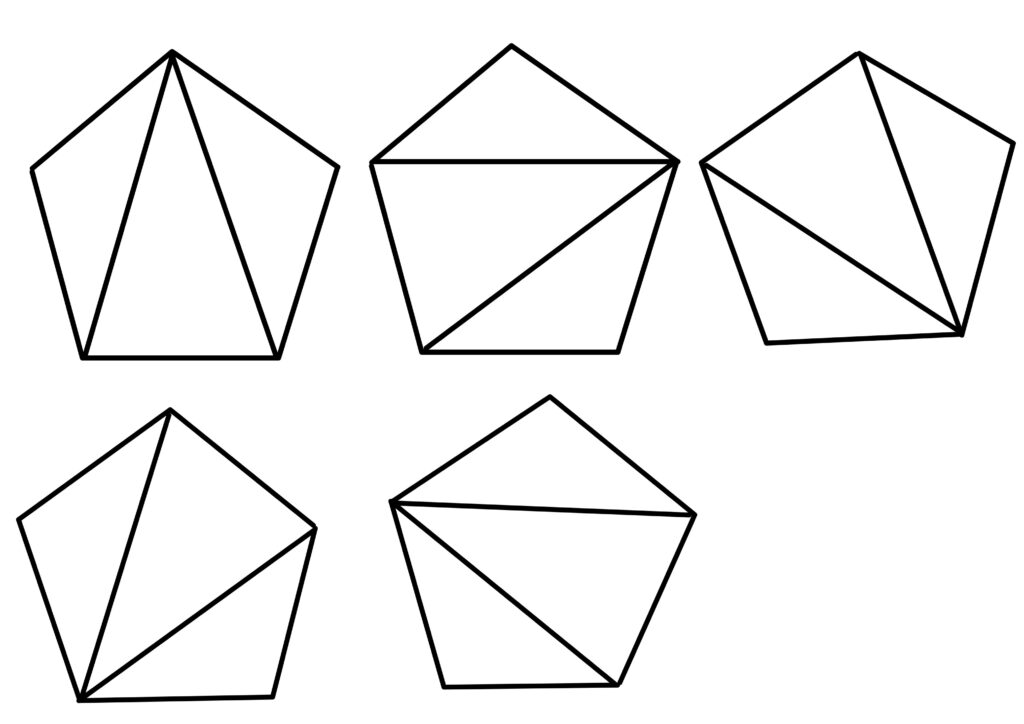
最大で2回で済みます。
正六角形の場合
正六角形を三角形で分割するような対角線の引き方はたくさんありますが、ピックアップすると以下のようなものがあります。

実験の結果
もっと実験すればよいのかもしれませんが、そのようにすれば結局13角形までたどり着いてしまいますので、エレガントない解答ではないと思い、やめました。
実験してみたものの、あまり芳しい結果は得られませんでした。
修士のときの指導教員の言葉を思い出しました。
数学に限らず、筆者の基本的な思考の流れとして「具体→抽象」という考え方をします(読者の皆様もこのような流れで考える方が多いのではないでしょうか)。
それゆえ、先の通り実験っぽいことをして具体例を出してみたりだとかをしてから問題に取り掛かることが多いです。
修士のとき、ある3次元の問題を考えていました。
しかし、うまく行かずどうしようかと悩んでいたところ、当時の指導教員から
と指導を受けたことがありました。
聞いた瞬間は「何言ってんだ。具体的な問題のほうがわかりやすいじゃないか。具体的な問題がわからない状態で同一般化しろというのだ。」と思いました。
とはいえ、やってみたら、確かに指導教員の指導の通りでした。
一般化をすることでむしろ分かりやすかったのです。
小話はおいておいて、要するに、13角形で考えるのではなく、一般に正\(n\)角形で考えようという話です。
一般化してみた
正\(n\)角形の頂点に\(X_1,\dots,X_n\)と名前をつけます。
これらを正\(n\)角形の対角線で接続することにして、その対角線で正\(n\)角形が三角形で分割されているようにします。
そもそもこのような対角線が何本あるか?というと\(n-3\)本です。
というのも、1つの頂点に注目して、その頂点から対角線を引くと、その頂点自身と、頂点の左右1つずつを覗いた頂点に向けて対角線が引けるから\(n-3\)本です。
つまり、\(X_i\)という頂点に目をつければ、対角変形によって対角線がすべて\(X_i\)を端点とするようにすれば、\(X_i\)は最大で\(n-3\)ボンの対角線の端点となっているわけです。
ということは、最大の対角変形の回数は\(n-3\)回じゃないか?と予想しました。
ただ、おそらくこの予想は間違いです。
なぜなら、「対角線1つにつき、1回だけしか対角変形しないのか?」と言われるとそうとも限らないからです。
ここまで来てタイムアップでした。
なんとも残念です。
投稿されたエレガントな解答
今回はエレガントな解答を紹介しているというよりは単に出題者からの解説が書かれているだけでした。
多角形に対角線を加えて三角形に分割した図形をその多角形の三角形分割と呼ぶことにします。まず、一般に、正\(n\)角形のどんな2つの三角形分割も対角変形を繰り返して互いに移り買うことを示して、正十三角形の場合に何回の対角変形で十分なのかを考えていくことにしましょう。
そこで、正\(n\)角形の\(n\)個の頂点を順に\(A_1,A_2,\cdots,A_n\)とし、その1つの三角形分割\(T\)において\(A_i\)を端点とする(接続している)対角線の本数を\(d_i\)とします。
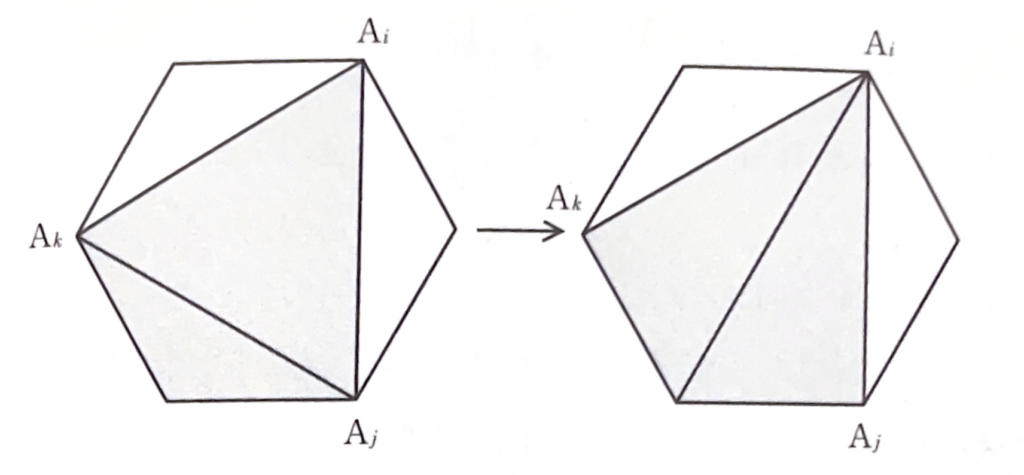
もし三角形\(A_iA_jA_k\)で、辺\(A_jA_k\)が三角形分割の対角線になっているものがあれば、その対角線\(A_jA_k\)をそれを含む四角形の中で切り替えて、\(A_i\)に接続する対角線に直すことができます。したがって、この変形を繰り返せば、すべての対角線が\(A_i\)に接続している状態を実現できることになります。
その最終状態では\(A_{i-1}\)と\(A_{i+1}\)と\(A_i\)を除く\(n-3\)個の頂点と\(A_i\)を結ぶ\(n-3\)本の対角線が存在しています。そこで、この特徴的な状態の三角形分割をここでは標準形と呼ぶことにします。
対角変形が対角線の総数を変えないことに注意すれば、標準形と同様に、どんな三角形分割にも\(n-3\)本の対角線があることがわかります。また、上述の対角変形を1回行うたびに、\(A_i\)に集まる対角線の本数は1本ずつ増えていくので、最初の状態からこの標準形を得るまでには、\(n-3-d_i\)回の対角変形が必要です。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p122-p124.
同様に、もう1つの三角形分割\(T^\prime\)を考えて、\(A_i\)に対角線を集めていきます。\(T^\prime\)において\(A_i\)に\(d_i^\prime\)本の対角線が接続しているなら、\(T^\prime\)から上と同じ標準形を作るには、やはり\(n-3-d_i\)回の対角変形が必要です。
ということは、まず、三角形分割\(T\)から上で述べたやり方で標準形を作り、それに\(T^\prime\)をその標準形にする変形の逆操作(これも対角変形)を施せば、\(T\)から\(T^\prime\)を作る1つの方法が得られることになります。
その際に実行する対角変形の回数は
$$
(n-3-d_i)+(n-3-d_i^\prime)=2n-6-(d_n+d_n^\prime)
$$
です。この値を小さくするためには、\(d_i+d_i^\prime\)の値を大きくすればよいので、\((d_i+d_i^\prime)\)がどのくらい大きくできるかを考えてみましょう。
まず、\(n-3\)本の対角線はそれぞれ2つの頂点に接続しているので、頂点に接続している対角線の本数である\(d_i\)を全部足すと対角線数の2倍になります。
$$
d_1+d_2+\cdots+d_n=2(n-3)
$$
これは\(d_i^\prime\)についても同様だから、両方を全部足すと、
$$
(d_1+d_1^\prime)+(d_n+d_n^\prime)+\cdots+(d_n+d_n^\prime)=4(n-3)
$$
になります。
この両辺を\(n\)で割れば、\((d_i+d_i^\prime)\)の平均値が求まります。当然、最大値は平均値以上なので、
$$
(d_i+d_i^\prime)\geq\frac{4(n-3)}{n}=4-\frac{12}{n}
$$
を満たす頂点\(A_i\)が存在します。さらに、\(n\geq 13\)ならば、\(\displaystyle\frac{12}{n}\)は\(1\)より小さくなるので、
$$
(d_i+d_i^\prime)\geq4
$$
となり、どんな2つの三角形分割も\(2n-10\)回以下の対角変形で移り合うことがわかりました。特に、正十三角形\((n=13)\)のときは、16回でOKということになります。これが問題の答えです。
標準形を経由させて移り合わせるという発想だったわけですね。
「経由しなくてもできる場合もあるよね?」と思いましたが、今回は最大でどれくらい対角変形が必要か、という話なので、標準形を経由するということを考えてOKなわけですね。
読者の皆様への挑戦状!
今から紹介する問題の解答は来週の日曜日に解説します!
3辺の長さが整数で、面積も整数になる三角形のうちで、面積が最小となるものを求めてください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p17.
(ヒント) 辺の長さが\(3,\ 4,\ 5\)の直角三角形は面積が\(6\)です。これより小さいものはあるのでしょうか?
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!




コメントをする