データの単位、基数変換、負の２進数、２進数の四則演算

本記事の内容

本記事は、基本情報技術者試験におけるデータの単位、基数変換、負の2進数、2進数の四則演算について、情報及びコンピュータの素人目線から説明する記事です。

本記事を読むに当たり、特別必要な知識はありません。

本ブログでは集合・論理・写像や実数の連続性、群論やグラフ理論など基礎的な大学数学(主として大学1,2年向けの数学)を解説しておりますので、そちらの記事もぜひご覧ください！

↓集合・写像・論理のシリーズ(の記事の一部)

「命題とは？」【論理と集合シリーズ】数学の文章を読むための論理的思考の基礎　その１

...

for-spring.com

2022.01.15

↓実数の連続性のシリーズ

実数の連続性のイメージをつかもう！

...

for-spring.com

2022.03.06

↓線形代数のシリーズ(の一部)

「行列って？」「正方行列、対角行列、単位行列」「転置」【線型代数学の基礎シリーズ】行列編 その1

...

for-spring.com

2022.06.30

本シリーズの立場 (読み飛ばしてOK)

筆者自己紹介にも書いていますが、筆者は学部、修士、博士(単位取得退学)と数学を専攻していました。
特に幾何学を主として学習していたので、情報理論やらコンピュータ理論などには疎いです。

そんなコンピュータ弱者が2023年4月から就職し、職場の関係上基本情報技術者試験を受験することになりました。

という方は案外多いのではないか？と思いました。
そこで、ど素人がど素人目線で基本情報技術者試験の勉強をした軌跡を共有することに価値があるのではないか、と感じ、本シリーズの執筆に至ります。

本シリーズでは、数学的視点も随時盛り込んでいこうとは思っていますが、それよりも「試験に合格すること」に重きを置く、すなわち

「どうすれば問題が解けるのか？」

というある種解き方に重きを置きます。

本記事のゴール

本記事のゴールは次の問題を解けるようになることです。

データの単位

コンピュータの世界では、日常生活ではあまり目にしない単位を使います。

ビット(bit)とバイト(byte)

最も基本的な単位です。

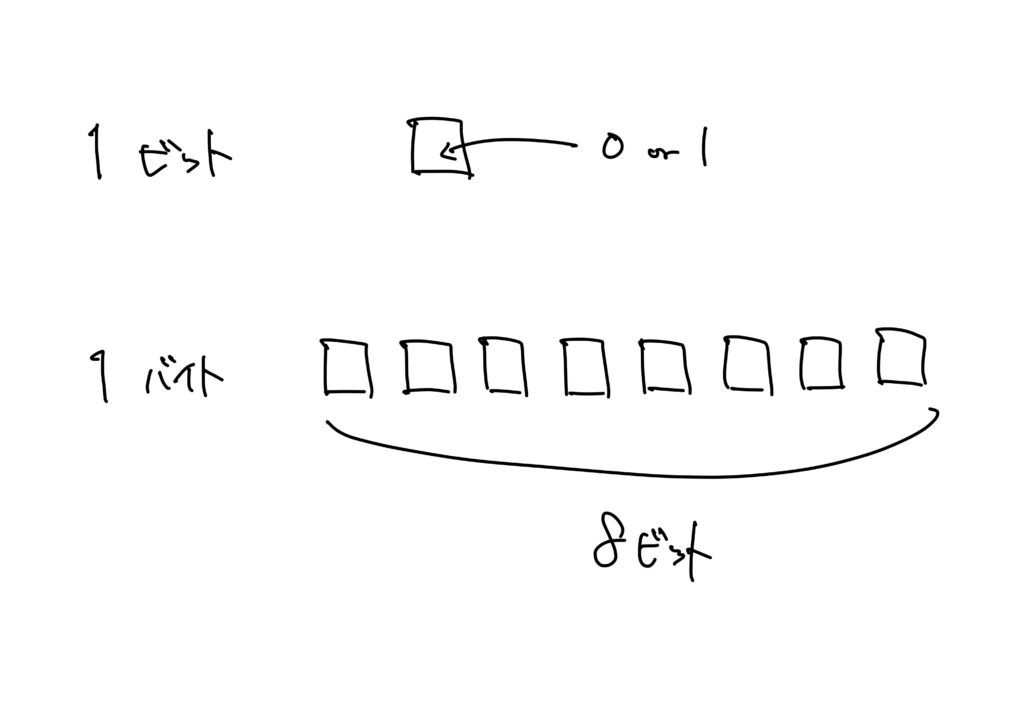
1ビットは「1」か「0」という2つの状態を表すことができるので、1byte=8bitですから、1バイトでは$2^8=256$通りの状態を表すことができます。

例1.

• 1ビット：0と1で$2^1=2$個
• 2ビット：00、01、10、11で$2^2=4$個
• 3ビット：000、001、010、011、100、101、110、111で$2^3=8$個
• 8ビット(1バイト)：$2^8=256$個

基本情報技術者試験では、10010011のように、0と1の並びで表された値のことををビット列、もしくはビットパターンといいます。

色々なデータの単位

キロバイトだのマイクロメートルだのは聞いたことがあると思います。
コンピュータの世界では、非常に大きな値や非常に大きな値を扱うことがありますので、それぞれのデータを簡潔に表す為に次の単位が用意されています。

単位	記号	10進数表記	累乗
テラ	T	1000000000000	$10^{12}$
ギガ	G	1000000000	$10^9$
メガ	M	1000000	$10^6$
キロ	k	100	$10^3$
基準		1	$10^0$
ミリ	m	0.001	$10^{-3}$
マイクロ	$\mu$	0.000001	$10^{-6}$
ナノ	n	0.000000001	$10^{-9}$
ピコ	p	0.000000000001	$10^{-12}$

数値の数え方

我々は$0,1,2,3,4,5,6,7,8,9$の10種類を使って数を表現しています。
つまり、10刻みで数を捉えている、ということになります。

コンピュータでは、そうではなく2刻み、16刻みで数を表現します。

10進数、2進数、16進数

少し数学の話をします。
10進数で3879という数は
$$3\times10^3+8\times10^2+7\times10^1+9\times10^0$$
と表現できます。
この表記を10進数表記と呼びます。
そして10を基数といいます。

2進数、16進数は基数がそれぞれ2、16であるような数の表現方法なのです。

10進数	0	1	2	3	4	5	6	7	8	9	10
2進数	0	1	10	11	100	101	110	111	1000	1001	1010

10進数	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
16進数	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F	10	11	12	13	14

16進数については、アラビア数字が10個しか無い関係上、10〜15はA〜Fのアルファベットで表現します。

※例は基数変換の部分で後述

小数

小数についても、本質的には同じです。

小数には大きく2種類あります。

• 有限小数：小数部の桁数に限りがある小数
• 無限小数：小数部の桁数に限りな無い小数

そして、無限小数には循環小数があります。

例えば、10進数の$0.123$という数は
$$1\times10^{-1}+2\times10^{-2}+3\times10^{-3}$$
と表現できます。
故に、小数も整数の場合と同じ型で表現できます。

基数変換

まず最初に躓くであろう部分(筆者は躓きました)がこの基数変換です。
読んで字の如し、基数を変換するやり方です。
ただ、先程述べた基数がわかっていればなんてことありません。

16進数→10進数、10進数→2進数の変換さえできれば、10進数→16進数の変換も本質的に同じであるため十分です。

16進数→10進数

簡単です。
16進数表現の2BD.C8という数は、
$$2\times16^{2}+{\rm B}\times16^{1}+{\rm D}\times16^0+{\rm C}\times16^{-1}+8\times16^{-2}$$
でした。
そして、B、C、Dはそれぞれ10進数表現では11、12、13です。
故に、
$$\begin{eqnarray} 2{\rm BD}.{\rm C}8&=&2\times16^{2}+{\rm B}\times16^{1}+{\rm D}\times16^0+{\rm C}\times16^{-1}+8\times16^{-2}\\ &=&2\times16^{2}+11\times16^{1}+13\times16^0+12\times16^{-1}+8\times16^{-2}\\ &=&512+176+13+\frac{12}{16}+\frac{8}{16^2}\\ &=&701.78125 \end{eqnarray}$$
となるわけです。

10進数→2進数

10進数表現の4.625を2進数表現に直す方法を述べます。
(ここでは手法を述べることに留めます)

やることは簡単で、与えられた数を整数部と小数部に分け、それぞれ変換します。

整数部

単純です。

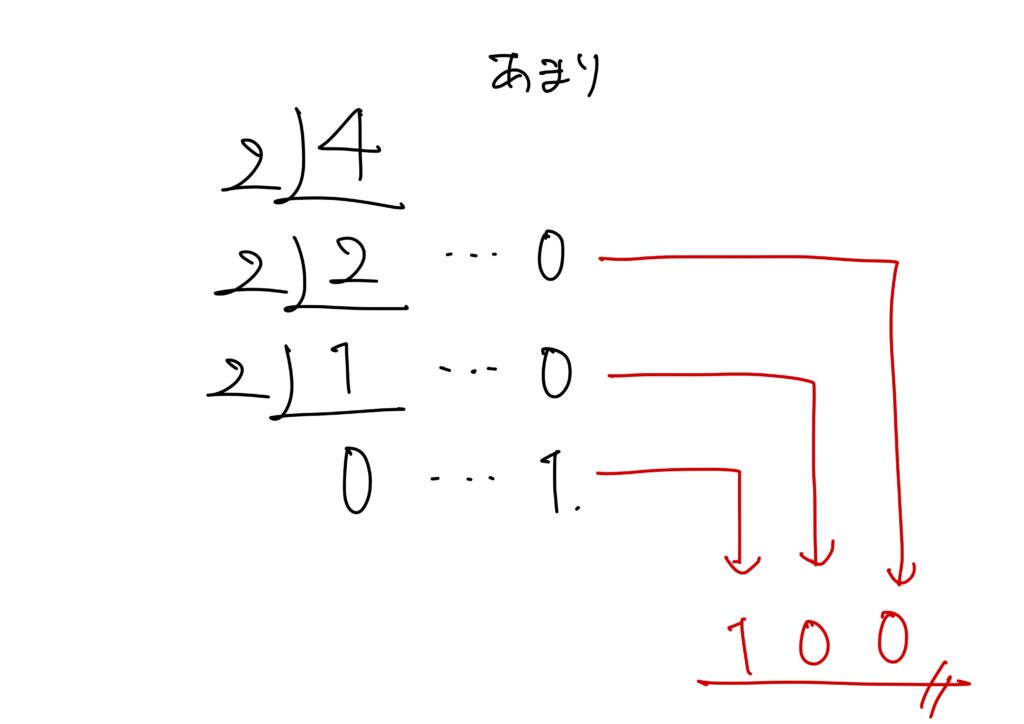
10進数を2進数の基数2で割り算を商が0になるまで続け、余りを逆に並べる

だけです。

小数部

1. 10進数小数に、2進数の基数2をかける。
2. 積のうち、整数部だけを取り出す。
3. 残った小数に更に2をかける。

これを小数部が0になるまで続けます。

本記事のゴールを解いてみる

まず、$7\div 32=0.2185$です。
整数部は0ですので、小数部だけを変換します。

負の2進数

負の整数を2進数で表現する方法には以下の3つがあります。

• 絶対値表現
• 1の補数表現
• 2の補数表現

絶対値表現

例2. 8ビットの2進数で表現

• $2=00000010$
• $-2=10000010$

1の補数表現

例3. 8ビットの2進数で表現

• $2=00000010$
• $-2=11111101$

2の補数表現

例4. 8ビットの2進数で表現

• $2=00000010$
• $-2=11111110$

２進数の四則演算

10進数の四則演算で慣れている我々は、2進数の四則演算を行おうとすると混乱します。
実際に筆者も混乱しました。

しかしながら、よくよく注意すれば加減法は問題ないし、積商も「シフト」の概念が分かればなんてことないのです。

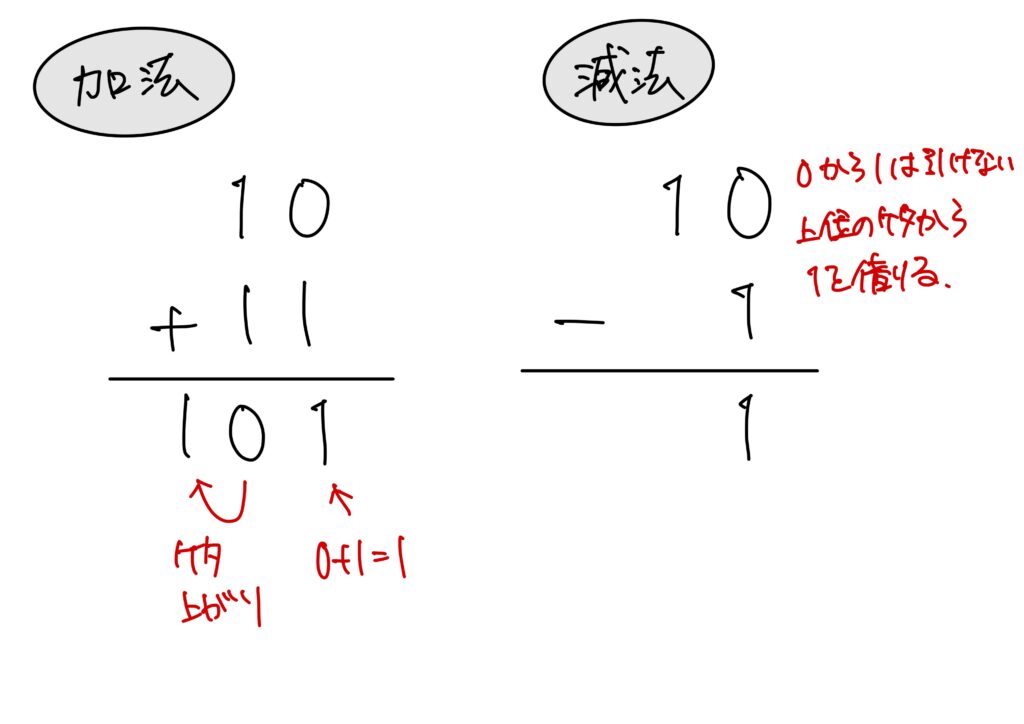
2進数の加減

筆算で行います。

2進数の積商

2進数表現の数を一旦10進数に変換して計算し、計算結果を再び2進数にすることでも解けますが、時間と手間がかかります。

そこで有用なのが「シフト演算」です。
次の章で述べます。

シフト演算

シフト演算には、以下の2種類が存在します。

• 論理シフト：正負を考慮しない(符号ビットを考慮しない)
• 算術シフト：正負を考慮する(符号ビットを考慮する)

「ビットをずらす」とは？

10進数表現において357という数のビットを左にずらしてみましょう。
すると、3570となります。
つまり、10倍されています。

一方で右にずらしてみると、35.7となります。
これは$\displaystyle\frac{1}{10}$倍されています。

これは2進数でも同様で、「ビットをずらす」というのは、基数倍、基数分の1倍するという意味です。

すなわち、2進数表現においてビット列を$n$個分だけ左にずらすというのは、元の数を$2^n$倍すること、右にずらすというのは元の数を$\displaystyle\frac{1}{2^n}$倍するということになります。

論理シフト

ビット列を左右にずらした上で、

• ビット列からはみ出したビットを無視する。
• 空いたビットに「0」を入れる

算術シフト

論理シフトと異なり、符号を考慮するので、符号ビットを特別視して固定します。

つまり、符号ビットは据え置きで、それ以外のビットをずらす、というのが算術シフトです。

手順としては

• ビット列からはみ出したビットを無視する。
• 左方向にずらした場合は、空いたビットに0を入れる。
• 右方向にずらした場合は、符号ビットと同じ数を入れる。

シフト演算を使って本記事のゴールを解いてみる

$32=2^5$ですから、
$$7\div32=7\div2^5=7\times\frac{1}{2^5}$$
です。

$7$の2進数表現は111ですから、右に5ビットだけずらせば良いです。
故に、答えは0.00111です。

簡単にできましたね。
基本情報技術者試験では時間が厳しいので、このシフトを積極的に使うと良いようです。

皆様のコメントをください！

就職して資格試験と仕事に関連する勉強に追われる日々が続いています。
皆さんは今年取った、または取ろうとしている資格はありますか？
是非コメントで教えてください。

結

今回は、基本情報技術者試験におけるデータの単位、基数変換、負の2進数、2進数の四則演算について、情報及びコンピュータの素人目線から説明しました。

問題が解けるということに重きを置き説明しました。

質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない！」などいただければお答えします！
Twitterでもリプ、DM問わず質問、コメントを大募集しております！

過去問などを解きたい場合は、過去問道場がおすすめです！