本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
問題を明示します。
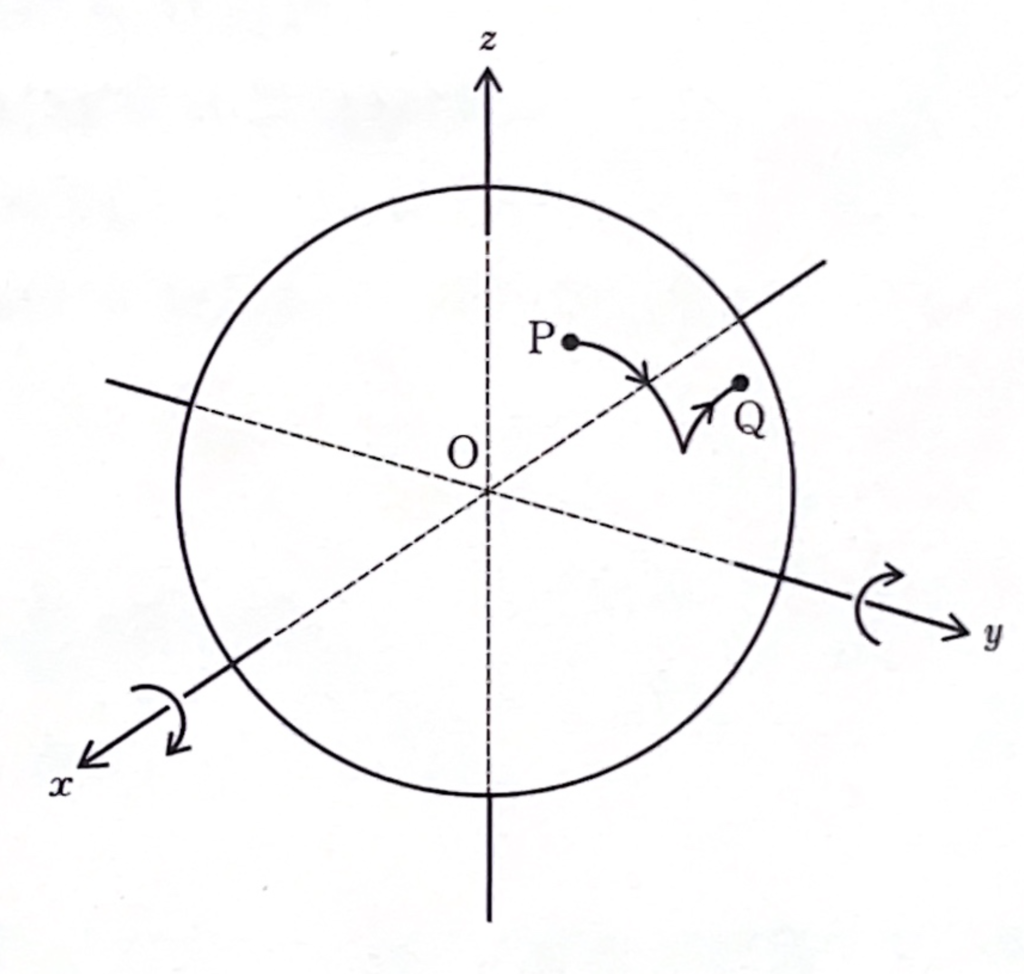
\(\theta\)を定数とします。\(OP=1\)であるような点\(P\)を\(x\)軸中心に角度\(\theta\)だけ回転し、さらに\(y\)軸を中心に角度\(\theta\)だけ回転してうつった点を\(Q\)とします。
原点を中心とする単位球面上の任意の位置に視点\(P\)をとりなおしたとき、線分\(PQ\)の長さの最大値はいくらになるでしょうか。
ただし\(x\)軸を中心とする角度は\(z\)軸から\(y\)軸の向きを正とし、\(y\)軸を中心とする角度は\(x\)軸から\(z\)軸の向きを正とします。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p19.
前回の問題は【1時間チャレンジシリーズ】挑戦㉒を御覧ください。
チャレンジの結果は…?
チャレンジの結果….解けました!
筆者の印象としては、別段難しい訳ではありませんでしたが、少々計算量が多いかな?といったところです。
しかも、真正直な方針で解けました。
筆者の解答を紹介します。
\(P(x,y,z)\)、\(Q(u,v,w)\)とします。
3次元空間における\(x\)軸、\(y\)軸に対して\(\theta\ [{\rm rad}]\)回転を表す行列はそれぞれ以下です。
- \(x\)軸に対する回転行列\(A\)
$$
A=
\begin{pmatrix}
1&0&0 \\
0&\cos\theta&-\sin\theta\\
0&\sin\theta&\cos\theta
\end{pmatrix}
$$ - \(y\)軸に対する回転行列\(B\)
$$
B=
\begin{pmatrix}
\cos\theta&0&\sin\theta \\
0&1&0\\
-\sin\theta&0&\cos\theta
\end{pmatrix}
$$
ここで、\(P\)を\(x\)軸まわりに\(\theta\)だけ回転させた点を\(R(x^\prime,y^\prime,z^\prime)\)と書くことにします。
すると、\((x,y,z)\)、\((x^\prime,y^\prime,z^\prime)\)および\((u,v,w)\)は次を満たします。
\begin{eqnarray}
\begin{pmatrix}
x^\prime\\
y^\prime\\
z^\prime
\end{pmatrix}
&=&
A\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}=
\begin{pmatrix}
1&0&0 \\
0&\cos\theta&-\sin\theta\\
0&\sin\theta&\cos\theta
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\\
\begin{pmatrix}
u\\
v\\
w
\end{pmatrix}
&=&
B\begin{pmatrix}
x^\prime\\
y^\prime\\
z^\prime
\end{pmatrix}=
\begin{pmatrix}
\cos\theta&0&\sin\theta \\
0&1&0\\
-\sin\theta&0&\cos\theta
\end{pmatrix}
\begin{pmatrix}
x^\prime\\
y^\prime\\
z^\prime
\end{pmatrix}
\end{eqnarray}
したがって、\(P(x,y,z)\)と\(Q(u,v,w)\)との関係式は
\begin{eqnarray}
\begin{pmatrix}
u\\
v\\
w
\end{pmatrix}&=&BA
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\\
&=&
\begin{pmatrix}
\cos\theta&0&\sin\theta \\
0&1&0\\
-\sin\theta&0&\cos\theta
\end{pmatrix}
\begin{pmatrix}
1&0&0 \\
0&\cos\theta&-\sin\theta\\
0&\sin\theta&\cos\theta
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\\
&=&
\begin{pmatrix}
\cos\theta&\sin^2\theta&\sin\theta\cos\theta \\
0&\cos\theta&-\sin\theta\\
-\sin\theta&\sin\theta\cos\theta&\cos^2\theta
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}\\
&=&
\begin{pmatrix}
x\cos\theta+y\sin^2\theta+z\sin\theta\cos\theta \\
y\cos\theta-z\sin\theta\\
-x\sin\theta+y\sin\theta\cos\theta+z\cos^2\theta
\end{pmatrix}
\end{eqnarray}
となります。
\(P(x,y,z)\)と\(Q(u,v,w)\)との距離は
\begin{eqnarray}
PQ^2&=&(x-u)^2+(y-v)^2+(z-w)^2\\
&=&\left( x-x\cos\theta-y\sin^2\theta-z\sin\theta\cos\theta\right)^2\\
&&+\left(y- y\cos\theta+z\sin\theta\right)^2\\
&&+\left( z+x\sin\theta-y\sin\theta\cos\theta-z\cos^2\theta\right)^2\\
&=&2\left( 1-\cos\theta\right)\left\{
x^2+y^2+z^2\left( 1+\cos\theta\right)-xy\left( 1+\cos\theta\right)-xz\sin\theta-yz\sin\theta
\right\}
\end{eqnarray}
です。
ここで、\(P(x,y,z)\)は単位球上の点なので、\(x^2+y^2+z^2=1\)を満たすから
\begin{eqnarray}
PQ^2&=&2\left( 1-\cos\theta\right)\left\{
x^2+y^2+z^2\left( 1+\cos\theta\right)-xy\left( 1+\cos\theta\right)-xz\sin\theta-yz\sin\theta
\right\}\\
&=&\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)-\left\{x\sin\theta+y\sin\theta+z\left( 1-\cos\theta\right)\right\}^2
\end{eqnarray}
となります。
さて、この式に注目すると、
\begin{eqnarray}
\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)-\left\{x\sin\theta+y\sin\theta+z\left( 1-\cos\theta\right)\right\}^2\\
&\geq&\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)
\end{eqnarray}
となります。
もし\(PQ^2=\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)\)となるような\(x,y,z\)が存在すれば、\(PQ^2\)の最大値は\(\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)\)と言えます。
うまく計算すれば、
$$
(x,y,z)=\left( \frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0\right)
$$
のとき、\(PQ^2=\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)\)を満たしますので、求める最大値は
$$
\sqrt{\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)}
$$
となります。
投稿されたエレガントな解答を紹介します!
筆者の解答と似ている解法については省略します。
(前略)
解答2 1回目、2回めの回転を表す行列をそれぞれ\(R_1\)、\(R_2\)とおくと
$$
R_1=
\begin{pmatrix}
1&0&0 \\
0&\cos\theta&-\sin\theta\\
0&\sin\theta&\cos\theta
\end{pmatrix},\quad
R_2=
\begin{pmatrix}
\cos\theta&0&\sin\theta \\
0&1&0\\
-\sin\theta&0&\cos\theta
\end{pmatrix}
$$
\(v=\overrightarrow{OP}\)とおくと\(\overrightarrow{OQ}=R_2R_1v\)、\(\overrightarrow{PQ}=\left(R_2R_1-E \right)v\)となる。(ただし、\(E\)は単位行列。) このとき、\(PQ^2={}^t\!v{}^t\!\left(R_2R_1-E \right)\left(R_2R_1-E \right)v\)となるので、
\begin{eqnarray}
S&=&{}^t\!\left( R_2R_1-E\right)\left( R_2R_1-E\right)\\
&=&\left( 1-\cos\theta\right)
\begin{pmatrix}
2&-\left( 1+\cos\theta\right)&-\sin\theta\\
-\left( 1+\cos\theta\right)&2&-\sin\theta\\
-\sin\theta&-\sin\theta&2\left( 1+\cos\theta\right)
\end{pmatrix}
\end{eqnarray}
とおくと、\(\left|v\right|=1\)なる\(v\)について\({}^t\!vSV\)の最大値を求めればよい。\(S\)は実対称行列なので、この最大値は\(S\)の固有値のうちで最大のものに等しい。\(S\)の固有多項式を計算すると
$$
\det\left( \lambda E-S\right)=\lambda\left( \lambda-\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)\right)^2
$$
となり、固有値は\(0\)と\(\left(1-\cos\theta \right)\left(3+\cos\theta \right)\)(重複度2)。\(\left(1-\cos\theta \right)\left(3+\cos\theta \right)\)のほうが大きいので、\(PQ\)の最大値は\(\sqrt{\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)}\)(答)となる。この解法はスマートですが、固有値の計算がめんどうなのが難点です。
解答3 2界の回転の合成変換を表す行列は、上で定義した\(R_1\)、\(R_2\)を用いて、
$$
R_2R_1=
\begin{pmatrix}
\cos\theta&\sin^2\theta&\sin\theta\cos\theta \\
0&\cos\theta&-\sin\theta\\
-\sin\theta&\sin\theta\cos\theta&\cos^2\theta
\end{pmatrix}
$$
とかける。ここで
$$
u=
\begin{pmatrix}
1\\
1\\
\displaystyle\tan\frac{\theta}{2}
\end{pmatrix}
$$
とおくと、\(R_2R_1u=u\)であることが、具体的に計算することにより確かめられる。すなわち\(R_2R_1\)はベクトル\(u\)を軸に回転を表すので、この回転でもっとも移動する点はこの回転の赤道上にある。つまり、\(u\perp \overrightarrow{OP_0}\)となる\(P_0\)が\(PQ\)の最大値を与える。たとえば\(P_0\)を\(\displaystyle\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0 \right)\)とおいて具体的に計算することにより、求める最大値\(\sqrt{\left( 1-\cos\theta\right)\left( 3+\cos\theta\right)}\)(答)を得る。2回の回転の合成写像を\(f\)、平面\(x=y\)についての面対象変換を\(g\)とおくと、\(g\)は\(x\)軸と\(y\)軸をいれかえ、さらに回転の向きを逆にするので、\(g^{-1}\circ f\circ g=f^{-1}\)であることがわかります。\(f\)は後述の系にあるように回転軸をもちますが、この式はこの回転軸が平面\(x=y\)の上にのっていることを意味します。つまり上の\(P_0\)はこの平面の法線ベクトルである\(\displaystyle\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0 \right)\)にとれることが分かります。
(中略)
さて、一般に次の事実が成り立ちますが、これを知っていると見通しよく計算をすすめることができます。解答3では下の系のみを用いて解くことになりますが、次の解答4では補題と系をみとめて解くことになります。
補題 球面から自分自身への向きを保つ等長写像は固定点をもつ。
証明 この写像を表す行列は正規直交行列だが、この行列が固有値\(1\)をもつことをいえばよい。直交行列なので角固有値の絶対値は\(1\)である。また、正規行列なので3つの固有値の積は\(1\)である。固有値がすべて実数のとき、各固有値は\(\pm1\)だが、3つの固有値の積が\(1\)なので、少なくとも1つは\(1\)になる。実数でない固有値\(\lambda\)をもつとき、実行列なので\(\overline{\lambda}\)も固有値にもつが、\(\lambda\overline{\lambda}=\left|\lambda\right|^2=1\)に注意すると、残りの1つは\(1\)になることがわかる。系 球面から自分自身への向きを保つ等長写像は、恒等写像か、ある軸を中心にする回転である。
証明 上の補題よりこの写像は固定点をもつので、この固定点と球の中心をとおる直線を軸にする回転(特別の場合として、恒等写像)にならざるをえないことが、等長写像であることを用いて示される。解答4 2つの回転の合成写像を表す行列は上で定義した\(R_1\)、\(R_2\)を用いて\(R_2R_1\)とかけるが、これは上の系より
$$
\begin{pmatrix}
\cos\omega&-\sin^2\omega&0 \\
\sin\omega&\cos\omega&0\\
0&0&1
\end{pmatrix}
$$
と共役になる。ただし\(\omega\)は合成写像の回転角である。(恒等写像のときは\(\omega=0\)とする。)共役な行列は対角和が等しいので、
$$
2\cos\theta+\cos^2\theta=2\cos\omega+1
$$
を得る。球面を回転したときもっとも移動する点はその回転の赤道上の点であり、問題の場合、赤道は半径\(1\)の円でこれを\(\omega\)回転することになるので、赤道上の各{\rm T}年の移動距離は\(\displaystyle2\sin\frac{\omega}{2}\)になる。よって求める最大値は
$$
2\sin\frac{\omega}{2}=\sqrt{2(1-\cos\omega)}=\sqrt{-\cos^2\theta-2\cos\theta+3}\tag{答}.
$$(中略)
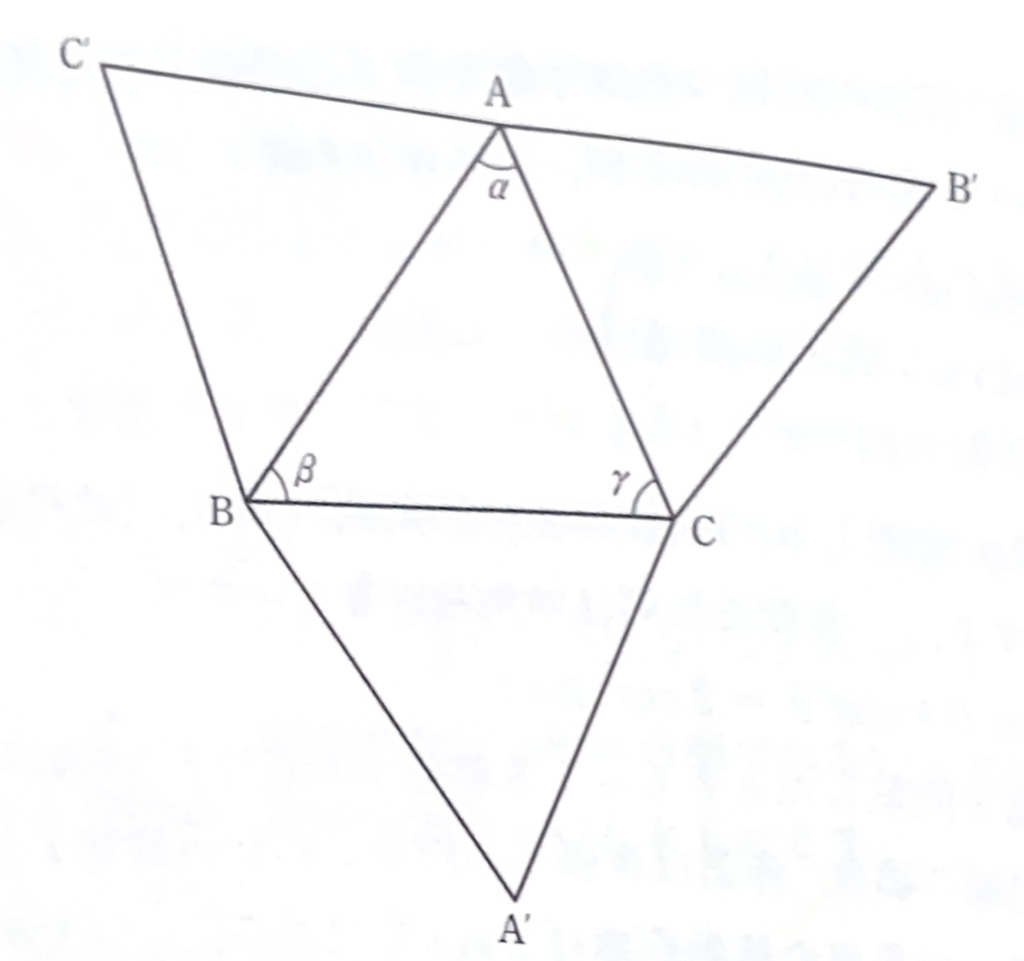
解答5 一般に単位球面上の球面3角形\(ABC\)について\(\angle A,\ \angle B,\ \angle C\)の大きさが\(\alpha,,\ \beta,\ \gamma\)であったとする。大円\(\stackrel{\huge\frown}{AB}\)について\(C\)と対象な点を\(C^\prime\)、大円\(\stackrel{\huge\frown}{BC}\)について\(A\)と対象な点を\(A^\prime\)、大円\(\stackrel{\huge\frown}{CA}\)について\(B\)と対象なてんを\(B^\prime\)とする。3点\(A,\ B,\ C^\prime\)を、点\(B\)を中心に\(2\beta\)回転すると、それぞれ\(A^\prime,,\ B,\ C\)に移り、さらに点\(C\)を中心に\(2\gamma\)回転すると、\(A,\ B^\prime,\ C\)に移る。すなわちこの2つの回転の合成は点\(A\)の合成は点\(A\)を中心にする\(-2\alpha\)回転である。
さて、問題の場合は\(2\beta=2\gamma=\theta\)、\(\displaystyle\stackrel{\huge\frown}{BC}=\frac{\pi}{2}\)のときに相当する。球面3角形の余弦定理より、
$$
\cos\alpha=-\cos\beta\cos\gamma+\sin\beta\sin\gamma\cos\stackrel{\huge\frown}{BC}=-\cos^2\frac{\theta}{2}
$$
である。合成写像の回転角は\(2\alpha\)なので、解答4と同様に考えて、求める最大値は
$$
2\sin\alpha=2\sqrt{1-\cos^4\frac{\theta}{2}}\tag{答}
$$(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p156-p160.
読者の皆様への挑戦状!ぜひ解いてみて下さい!
以下の問題は来週解説します。
シルクロードの遺跡を発掘していた数セミ隊は、ネストリウス派の教会跡と思われるところから青銅の箱に収められた文書を発見した。それはソグド文字で記載される交易に関する文書群であった。それによれば、この遺跡の周辺にはなお5つの都市が存在していたことが解る。現在発掘中の都市を\(A_1\)とする。この他に\(A_2,A_3,B_1,B_2,B_3\)という都市が存在した。文書によれば、都市\(A_i\)から\(B_j\)へは\(i+j\)日かかるという。また、ある断簡によれば、\(A_x\)から\(B_y\)へ向かうカラバンと\(B_w\)から\(A_z\)に向かうキャラバンとが、その道筋で出会ったときに何か争いを起こしたと思われるが、\(x\neq z\)、\(y\neq w\)であるらしいことは解るものの、\(x,y,z,w\)そのものは読みとれない。
各都市の間の道は直線的であったとし、かつその間を移動するのにかかる日数はちょうど距離に比例すると仮定して、その位置関係を探って今後の発掘の参考にしたい。
- いま簡単のために\(x=1\)、\(y=2\)、\(z=2\)、\(w=1\)を仮定してその位置関係を考えて見たところ、この仮定の下ではなんと\(A_1\)、\(A_2\)、\(B_1\)、\(B_2\)は一直線上に存在することが解った。
- 上記の仮定を置かずにさらにいろいろと考えたところ、実はすべての6つの都市が一直線上にあることが解った。
さて、上記のことを確認していただきたい。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p19-p20.
前回の問題は【1時間チャレンジシリーズ】挑戦㉒を御覧ください。
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!




コメントをする