本記事の内容
本記事は「関数が極限を持つならば、制限した関数も同じ極限を持つ」、「連続関数の制限もまた連続関数である」ということを証明する記事です。
本記事を読むにあたり、多変数ベクトル値関数の極限について知っている必要があるため、その際は以下の記事を参照してください。
まずは、写像、特に関数の制限について説明します。
写像の”制限”って?
写像の”制限”を一言で言えば、「定義域を狭めた写像」のことです。
「どういうことかネ?」となると思うので、例を挙げます。
例1.(料理を食べるときに使う食器との対応規則)
\(X=\{カレー,\ ステーキ,\ おにぎり,\ チャーハン\}\)、\(Y=\{スプーン,\ ナイフ,\ 手,\ 足\}\)として、\(f:X\to Y\)が
- \(f(カレー)=スプーン\)、
- \(f(ステーキ)=ナイフ\)、
- \(f(おにぎり)=手\)、
- \(f(チャーハン)=スプーン\)
で定められているとしましょう。
このとき、\(X\)の部分集合として\(X^\prime=\{カレー,\ おにぎり,\ チャーハン\}\)を考えます。
すなわち、\(X^\prime\)は\(X\)の中でご飯物を集めた集合です。
\(X^\prime\subset X\)ですので、当然ながら\(X^\prime\)の任意の要素に対して、\(Y\)の要素がただ1つ対応しています。
しかも、その対応規則は\(f\)と同じです。
つまり、
- \(f^\prime(カレー)=スプーン\)、
- \(f^\prime(おにぎり)=手\)、
- \(f^\prime(チャーハン)=スプーン\)
で定められる\(f^\prime:X^\prime \to Y\)を考えることができます。
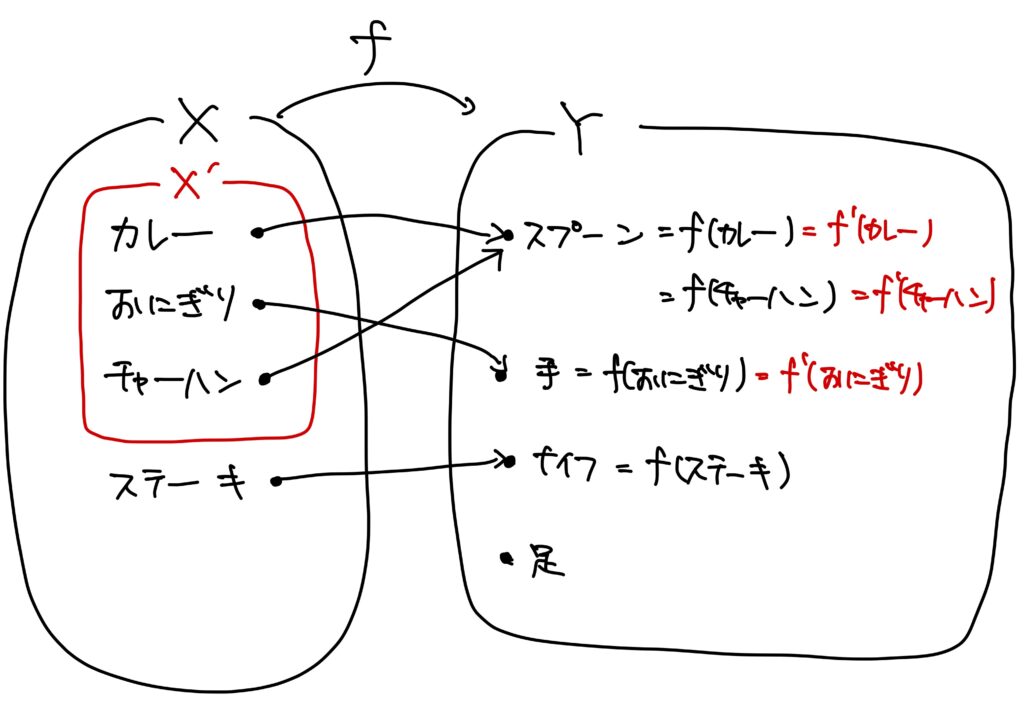
この\(f^\prime\)を\(f\)の\(X^\prime\)への制限と言います。
例2. \(g:\mathbb{R}\to\mathbb{R}\)が \(g(x)=\sin x\)で定められているとします。
【論理と集合シリーズ】写像編 その9で説明したとおり、この\(g\)は、というより\(\sin\)は全単射ではありません。
従って、逆写像は存在しません。
しかしながら、「定義域と終域を”絞る”ことで全単射が作れる」のでした。
つまり、定義域を\(\mathbb{R}\)から\(\displaystyle\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)に、終域を\(\mathbb{R}\)から\([-1,1]\)に”絞る”ことで全単射になるため、この場合には逆写像が存在するのでした。
新たにこの写像に\(g^\prime:\displaystyle\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\to[-1,1]\)と名前を付けましょう。

実はこれは\(g\)の\(\displaystyle\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\)への制限だったのです。
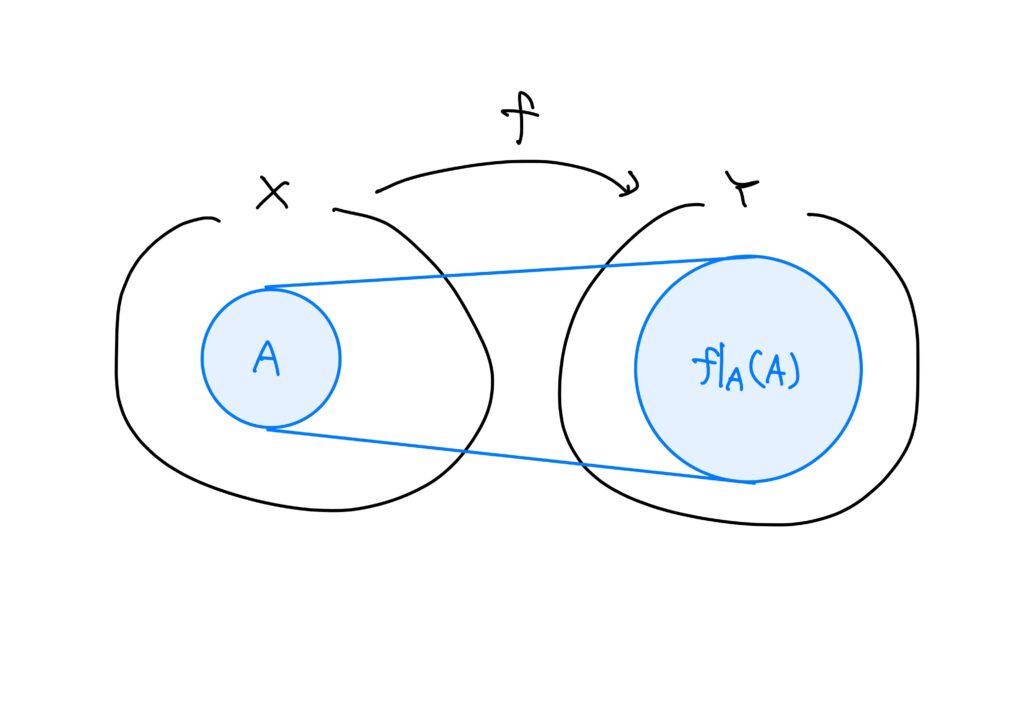
この例は終域も絞っていますが、一般に、写像の制限は定義域を絞ることです。
以上のことを数学的に表すと次です。
すなわち、\(f|_A:A\to Y\)は $$ (\forall x\in A)\quad f|_A(x)=f(x) $$ で定められる写像である。
では、定義域を制限した関数の極限について考えてみます。
関数が極限を持つならば、制限した関数も同じ極限を持つ
まずは主張を明示します。
すなわち、 \(\Omega^\prime\subset \Omega\subset \mathbb{R}^n\)とし、\(\Omega^\prime\neq \emptyset\)とする。 \(\boldsymbol{f}:\Omega\to\mathbb{R}^m\)とするとき、\(\boldsymbol{f}\)の\(\Omega^\prime\)への制限\(\boldsymbol{f}|_{\Omega^\prime}:\Omega^\prime\to \mathbb{R}^m\)が\(\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{x})\)で定められる。 このとき、\(\boldsymbol{a}\in\bar{\Omega^\prime}\)、\(\boldsymbol{A}\in\mathbb{R}^m\)、\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A}\)であれば、 $$ \lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})=\boldsymbol{A} $$ が成り立つ。
※ちょっとした注意※\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})\)を\(\displaystyle\lim_{\substack{\boldsymbol{x}\in \Omega^\prime\\ \boldsymbol{x}\to\boldsymbol{a}}}\boldsymbol{f}(\boldsymbol{x})\)で表す場合もあります。
証明
誠に簡単です。
というより明らかと言いたいところです。
言いませんけどね(笑)
仮定から\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{A}\)ですので、
$$
(\forall \epsilon>0)\ (\exists \delta>0)\ {\rm s.t.}\ \left(\forall \boldsymbol{x}\in\Omega :0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon\right)
$$
今、\(\Omega^\prime\subset \Omega\)です。
部分集合とはどういうものだったかを思い出すと、
$$
\forall\boldsymbol{x}\in\Omega^\prime\Rightarrow \boldsymbol{x}\in \Omega
$$
です。
従って、\(0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\)を満たす任意の\(\boldsymbol{x}\in\Omega^\prime\)は、\(|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon\)を満たしています。

これはまさに
$$
(\forall \epsilon>0)\ (\exists \delta>0)\ {\rm s.t.}\ \left(\forall \boldsymbol{x}\in\Omega^\prime :0<|\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon\right)
$$
を表しているため、\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})=\boldsymbol{A}\)です。
証明終わり
この命題3.の系として次が成り立ちます。
すなわち、 \(\Omega^\prime\subset \Omega\subset \mathbb{R}^n\)とし、\(\Omega^\prime\neq \emptyset\)とする。 \(\boldsymbol{f}:\Omega\to\mathbb{R}^m\)とするとき、\(\boldsymbol{f}\)の\(\Omega^\prime\)への制限\(\boldsymbol{f}|_{\Omega^\prime}:\Omega^\prime\to \mathbb{R}^m\)が\(\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{x})\)で定められる。 このとき、\(\boldsymbol{a}\in\bar{\Omega^\prime}\)であり、\(\boldsymbol{f}\)が\(\Omega\)で連続、すなわち、任意の\(\boldsymbol{a}\in\Omega\)に対して\(\displaystyle\lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{a})\)であれば、 $$ \lim_{\boldsymbol{x}\to\boldsymbol{a}}\boldsymbol{f}|_{\Omega^\prime}(\boldsymbol{x})=\boldsymbol{f}(\boldsymbol{a}) $$ が成り立つ。
この系4.の証明は命題3.の証明を\(\boldsymbol{A}\)を\(\boldsymbol{f}(\boldsymbol{a})\)に書き換えれば良いので省略します。
なんでこの事実が必要なのかネ?
命題3.を実際に証明してみると「簡単だし当然じゃね?」となりますし、「だから何?」という感じですが、なぜこの事実を記事化したかを話します。
正直、オチとしては「詳しくは次回以降話します」ということです。
多変数関数の場合、一見極限が存在しそうでも存在しない場合があります。
それは、極限への近づき方がありとあらゆる方向からと沢山あるからです。
より端的に言えば、
ということです。
これらを混同してしまいがちですが、違います。
このことを具体例と共に説明するためにこの事実を使うため、今回は制限の極限について話しました。
結
今回は関数が極限を持つならば、制限した関数も同じ極限を持つ」「連続関数の制限も連続関数である」ということを説明、証明しました。
要は、
ということです。
次回は関数の発散の一部について解説します。
※5/18追記 次回に多変数実数値関数の注意を書くことにします。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする