本記事の内容
本記事はワイエルシュトラスの上限公理をデデキントの定理から導き、それを説明、証明する記事です。
本記事を読むにあたり、デデキントの定理を知っている必要があるため、以下の記事も合わせて御覧ください。
また、上限についても知っている必要があるため、以下の記事も合わせて御覧ください。
ワイエルシュトラスの上限公理
ワイエルシュトラスの上限公理は解析学の中でも非常に基本的な事実です。
先述しましたが、この公理はデデキントの定理から証明できます。
若干ネタバラシなのですが、その逆、すなわちワイエルシュトラスの上限公理を認めれば、デデキントの定理を示すことができます。
デデキントの定理は何だったかというと、以下です。
- Aには最大値が無く、Bには最小値rがある。
- Aには最大値rがあり、Bには最小値がない。
証明は【解析学の基礎シリーズ】実数の連続性編 その2を御覧ください。
ワイエルシュトラスの上限公理は「天井があるような集合には上限と呼ばれるMAX値（最大値ではない）が実数に存在しますよ、ということだ」と先に述べました。
これを今まで解説したことを思い出すと、上限は「その数よりも”ほんのちょっとでも”小さい数は上界じゃないぜ」という「その数」のことでした。
これはつまり、「どんな実数にもその十分近くにまた実数がある」ということが保証されなければ上限なんていうものは存在し得ない、ということになります。
ワイエルシュトラスの上限公理を認める、ということはこの上限の存在を保証することで、どんな実数にもその十分近くにまた実数があることを認めている、ということなのです。
論理式で書けば、
です。
ちなみに、公理ということをざっくり述べておくと「議論を行うための大前提」のことです。
ワイエルシュトラスの上限公理はデデキントの切断からデデキントの定理を導出することで、デデキントの定理から証明が可能なので、そういう言う意味では公理ではありません。
ただし、後に述べるようにこれら２つは同値なので、ワイエルシュトラスの上限公理を大前提として議論をすすめる立場もあります。
したがって、公理と呼んでいるのです。
証明
A⊂Rは空集合でなく、かつ上に有界であるとします。
また、Aの上界の集合をBとします。
このとき、C=Bc=R∖Bとおくと、(C,B)はRの切断となっています。
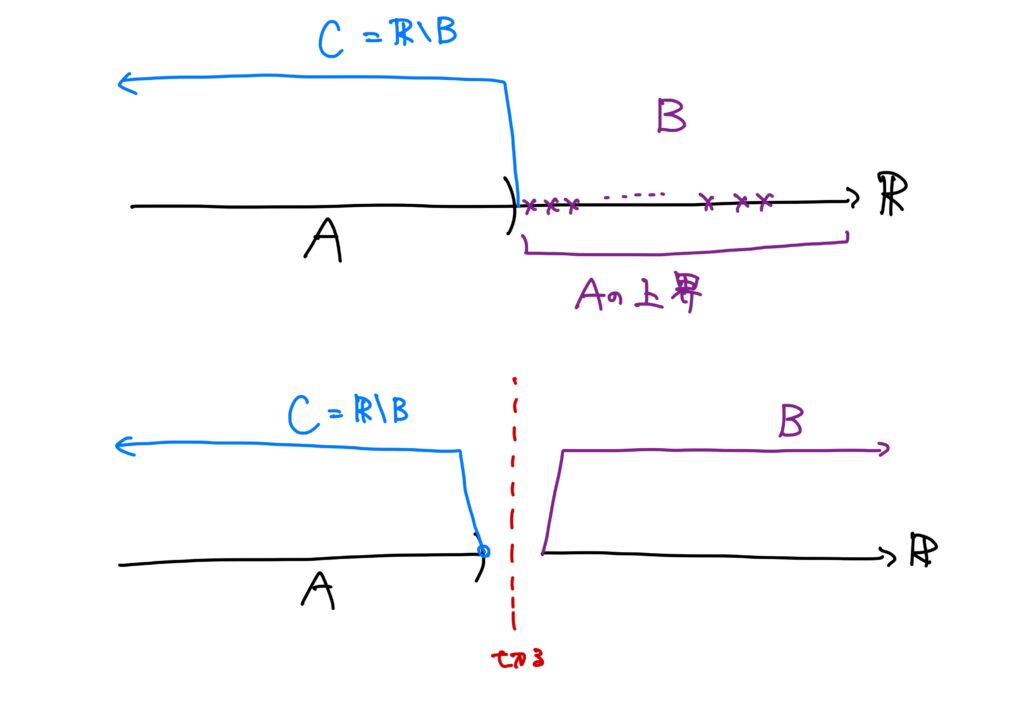
すなわち、次が成り立ちます。
- R=C∪B
「R⊂C∪BかつC∪B⊂R」を示せばOKです。（集合が等しいとはこれを示すことだった！）
任意のx∈Rに対して、xがAの上界であれば、x∈Rかつx∈Bです。
そうでなければ、x∈Rかつx∉Bです。
従って、x∈R∖Bまたはx∈Bが成り立つので、x∈R∖B∪B=C∪Bです。
任意のx∈C∪Bに対して、x∈Cであれ、x∈Bであれx∈Rです。
従って、R=C∪Bです。 - C∩B=∅
仮にC∩B≠∅とすると(背理法！)、あるzが存在してz∈C∩Bを満たします。
従って、「z∈Rかつz∉Bかつz∈B」が真である事になってしまいますが、これは偽であり矛盾です。 - C≠∅, B≠∅
B=∅であれば(背理法！)、Aに上界が存在しないことになりますが、これはAが上に有界であることに矛盾です。
あるx∈Aに対して、x−1∉Bです。
実際、x−1∈Bであれば、任意のx∈Aに対してx≤x−1を満たすことになり、0≤−1を得るため矛盾です。
加えて、x∈A⊂Rですから、x−1∈Rです。
従って、x−1∈R∖B=Cとなり、C≠∅です。 - c∈Cかつb∈Bならばc<b
任意のc∈CはAの上界ではないので、c∉Bであり、あるx0∈Aが存在してx0>c(cがAの上界であることの否定！)を満たします。
また、b∈Bにより、任意のx∈Aに対してx≤bが成り立ちます。
この命題は任意のx∈Aについて成り立つので、x0∈Aについても成り立ちます。
つまり、x0≤bが成り立ちます。
したがって、c<x0≤bですからc<bです。
故に(C,B)はRの切断です。
デデキントの定理から、ある実数rが存在して、
- Cには最大値が無く、Bには最小値rがある。
- Cには最大値rがあり、Bには最小値がない。
のいずれか一方が成り立ちます。
2.が成り立ったとしましょう。
つまりCには最大値rがあり、Bには最小値がないとします。
r∈Cであれば、(C,B)は切断ですので、r∉Bです。
従って、rはAの上界ではありません。
すなわち、x0>rを満たすようなx0∈Aが存在します。
これを論理式で書けば、
(∃x0∈A) s.t. x0>r
(rがAの上界であることの否定！)です。
ここで、r+x02はrとx0の間にある数(有理数とは限りません)であり、これをbとします。
すなわち、b=r+x02とおけば、
r<b<x0
を満たします。
これはbがAの上界でないことを表しています。
故にb∈Cです。
rはCの最大値ですから、任意のt∈Cに対して、t≤rを満たします。
b∈Cですからb≤rも成り立ちます。
従って、r<bとb≤rが同時に成り立つので矛盾です。
故に、2.の場合は起こり得ません。
すなわち、起こり得るのは1.の場合です。
つまり、Cには最大値は存在せず、Bには最小値rが存在します。
BとはAの上界の集合であり、上限とは上界の最小値ですから、rはAの上限です。
証明終わり
結
今回はワイエルシュトラスの上限公理をデデキントの定理から示しました。
これは「どんな実数のにもその十分近くにもまた実数がある。」という直感に対応します。
次回は「ワイエルシュトラスの上限公理とデデキントの定理は同値」です
乞うご期待！質問、コメントなどお待ちしております！
コメントをする
教えてください
CとBに切断してCに最大値ｒがあるなら上限で切断して上限ｒ
をCに含めたからだと思います。
その場合Cにｒを超える元が存在市内のでは無いかとおもいます。
名無しさん
ご質問ありがとうございます！
少々遅れてしまいましたが、回答させていただきます。
2.が成り立っていると仮定したので、
が成り立っています。
今、Cには最大値rが存在するのだから、
が成り立っています。
r∈Cで、(C,B)が切断なので、r∉Bです。
BはAの上界の集合だったので、r∉Bということは、rはAの上界ではありません。
今、rはAの上界ではないので、これの否定
(∃x0∈A) s.t. x0>r
が成り立っています。
ここで、
b=r+x02
はrとx0の間にある数です。
つまり
r<b<x0⋯①
です。
これはつまり
(∃x0∈A) s.t. x0>b
ということなので、これはbがAの上界でないことを表しています。
bがAの上界でないので、b∉Bです。
今、(C,B)は切断なので、b∉Bによりb∈Cです。
さて、rはCの最大値だったので、どんなCの要素tに対してもt≤rだから、
b≤r⋯②
です。
①と②からr<bとb≤rが同時に成り立ってしまったので、矛盾です。
思い出しておくと、デデキントの定理から
のどちらか１つが成り立っています。
これまでの話は「2.が成り立ったとすると」という仮定のもとで行った話で、そこで矛盾が発生したため、2.の場合は起こり得ない、ということになります。
デデキントの定理から1.と2.の「どちらか1つだけ」成り立つ、ということで、2.が成り立ったとすると矛盾が生じたため、1.が成り立つ、という結論になります。
いかがでしょうか…?
この回答にも不明点などあればぜひまたコメントをお願いします。
何度でも質問を受け付けておりますので、お気軽にご質問くださいませ。