「多変数ベクトル値関数の収束」【解析学の基礎シリーズ】多変数関数編 その2

本記事の内容

本記事は「多変数ベクトル値関数の収束」について解説する記事です。

本記事を読むにあたり、多変数ベクトル値関数とは何か、関数の極限について知っている必要があるため、その際は以下の記事を参照してください。

「多変数ベクトル値関数って？」【解析学の基礎シリーズ】多変数関数編 その1

本記事の内容本記事は「多変数ベクトル値関数って何？」ということについて解説する記事です。本記事を読むにあたり、「関数(写像)ってなんだっけ」ということを知っている必要があるため、その際は以下の記事を参照してください。また、点列について知って

for-spring.com

「関数の収束って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その２

本記事の内容本記事は関数の収束は数学的にどういうことかを説明し、実際に関数の収束を証明してみる記事である。本記事を読むにあたり数列の収束を理解し、関数の収束のイメージがついているとより理解しやすいと思われるので、その際は以下の記事を参照して

for-spring.com

関数の収束の復習と多変数ベクトル値関数の極限のイメージ

点列のときと同様に、多変数ベクトル値関数も関数なので極限を考えることができます。
「点列のときと同様に、成分ごとに考えれば今まで扱ってきた関数の極限に帰着できるのかネ？」といいうと注意が必要です。
というのも、点列は自然数に対してベクトルを対応させる写像だったからです。
どういうことかというと、点列は数列と定義域が同じですが、多変数ベクトル値関数は定義域の次元も変わります。
つまり、成分ごとに考えてもまだ多変数の関数の可能性があります。
とはいえ、形式的には今まで扱ってきた１変数実数値関数の極限と同じです。

というわけで、まずは1変数実数値関数の収束のイメージを軽く復習しましょう。

1変数実数値関数の収束の復習

「ちゃんと知りたい！」「ちゃんと思い出したい！」という方は【解析学の基礎シリーズ】関数の極限編 その1と【解析学の基礎シリーズ】関数の極限編 その2を参照してください。

ということでした。
厳密に論理式で書けば

ということです。
では多変数ベクトル値関数について見ていきましょう。

多変数ベクトル値関数の収束のイメージ

本質的には1変数実数値関数と同じです。
つまり、「ある点と距離が近い定義域の値に対しては、その値に対応する関数の値同士が十分近いときに収束するという。」というわけです。
この”値”が今までは実数でしたが、これからは”ベクトル”というだけです。
要は、多次元ではベクトルがベクトルに近づくということです。
しかし、数列と点列との関係よりも少々複雑なので、ちょっと踏み込んだ多変数ベクトル値関数の収束のイメージで少々語ることにします。

さて、「多次元のときも距離は絶対値なのかネ？」と思うかもしれません。
これは点列のときと同様で、ベクトルの距離は単なる絶対値では表現できません。
従って、ベクトルの大きさが距離になります。
記号で書けば、ベクトル$\boldsymbol{a}=(a_1,a_2,\cdots,a_n)^\top$の大きさ$|\boldsymbol{a}|$は
$$|a|=\sqrt{a_1^2+a_2^2+\cdots+a_n^2}$$
です。
(※これをEuclid(ゆーくりっど)距離と言ったりします。)
ただし、$\boldsymbol{a}^\top$はベクトル$\boldsymbol{a}$の行と列を入れ替えた(転置した)ベクトルのことです。

これで「ベクトル同士が十分近い」ということが表現できました。
では、多変数ベクトル値関数の収束を数学的に明示しましょう。

で？”多変数ベクトル値関数の収束”は何なのかネ？

今までの話を論理式で書く前に一つ記号を導入します。

閉包

閉包を論理式で書くとちょっとイメージが湧きにくいかもしれませんが、直感的には非常にシンプルです。
$\bar{I}$は区間$I$の両端を入れた区間でした。
$\bar{\Omega}$は領域$\Omega$の境界(縁)を入れた領域です。

これを論理式で書くために、1つ記号を導入します。
$$B(\boldsymbol{x};\epsilon)=\{\boldsymbol{y}\in\mathbb{R}^n|\ |\boldsymbol{x}-\boldsymbol{y}|<\epsilon\}$$
とします。
$B(\boldsymbol{x};\epsilon)$を開球といいます。
これは中心が$\boldsymbol{x}$で半径が$\epsilon$の球の表面を除いた($<$だから)球の領域です。
(要は境界を含まない球です。)
2次元の場合は円周を除いた円の領域です。
実際、$\boldsymbol{x}=(x_1,x_2,\cdots,x_n)^\top$、$\boldsymbol{y}=(y_1,y_2,\cdots,y_n)^\top$と書いたとき、
$$|\boldsymbol{x}-\boldsymbol{y}|=\sqrt{(y_1-x_1)^2+(y_2-x_2)^2+\cdots+(y_n-x_n)^2}<\epsilon$$
であり、
$$(x_1-y_1)^2+(x_2-y_2)^2+\cdots+(x_n-y_n)^2<\epsilon^2$$
です。
これはまさに球の内側の領域を表しています。
2次元の場合を考えてみるとより分かりやすいです。
$\boldsymbol{x}=(x_1,x_2)^\top$、$\boldsymbol{y}=(y_1,y_2)^\top$と書いたとき、
$$|\boldsymbol{x}-\boldsymbol{y}|=\sqrt{(y_1-x_1)^2+(y_2-x_2)^2}<\epsilon$$
であり、
$$(x_1-y_1)^2+(x_2-y_2)^2<\epsilon^2$$
です。
これはまさに円の内側の領域です。

開球を導入したところで、閉包を導入します。
先程閉包は領域の縁を含めた領域だ、と述べました。
これを論理式で書くと、
$$\bar{\Omega}=\{\boldsymbol{x}\in\mathbb{R}^n|\ (\forall \epsilon>0)\ B(\boldsymbol{x};\epsilon)\cap \Omega\neq \emptyset\}$$
です。
これだけ見ても「本当に$\Omega$の境界を含んだ領域なのかネ？」というように直感とはつながらないので、図で説明します。

で結局論理式で書くとどうなのかネ？

閉包を導入したところで、多変数ベクトル値関数の収束を論理式で書きます。

このように形式的には1変数実数値関数と何ら変わりません。
とはいえ、イメージが湧きにくいのも事実です。

実は、点列と同様に、多変数ベクトル値関数もベクトルの成分ごとの極限を考えれば良い、という定理があります。

結局のところ、成分ごとに極限を考えてOKということです。
高校数学のノリで言うところの「$\lim$はカッコの中に入れてOK」というわけです。

では証明に入りますが、点列のときとほとんど同じです。

証明

$(\Rightarrow)$の証明

示したいことは、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |f_i(\boldsymbol{x})-A_i|<\epsilon)$$
です。
今、
$$(\forall \epsilon_0>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon_0)$$
が成り立っているので、
$$|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|=\sqrt{(f_1(\boldsymbol{x})-A_1)^2+(f_2(\boldsymbol{x})-A_2)^2+\cdots+(f_m(\boldsymbol{x})-A_m)^2}<\epsilon_0$$
が任意の$\epsilon_0$で成り立っています。
$\epsilon_0$は任意なので、任意の$\epsilon>0$を用いて$\epsilon_0=\sqrt{\epsilon}$としても成り立ちます。
従って、
$$|\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|=\sqrt{(f_1(\boldsymbol{x})-A_1)^2+(f_2(\boldsymbol{x})-A_2)^2+\cdots+(f_m(\boldsymbol{x})-A_m)^2}<\sqrt{\epsilon}$$
が成り立っています。

ここで、$(f_i(\boldsymbol{x})-A_i)^2$は$1\leq i\leq m$で$0$以上です。
また、$\displaystyle \sum_{i=1}^m(f_i(\boldsymbol{x})-A_i)^2<\epsilon$なのですから、
どの$1\leq i\leq m$を満たす$i\in\mathbb{N}$についても$\displaystyle (f_i(\boldsymbol{x})-A_i)^2<\epsilon$でなければなりません。
従って、$\displaystyle M=\max_{i=1,2,\cdots,m} (f_i(\boldsymbol{x})-A_i)^2$とすると、$M<\epsilon$が成り立ちます。
故に$0<|\boldsymbol{x}-\boldsymbol{a}|<\delta$なる$\boldsymbol{x}\in\bar{\Omega}$に対して
$$(f_i(\boldsymbol{x})-A_i)^2\leq M<\epsilon$$
となります。
従って、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |f_i(\boldsymbol{x})-A_i|<\epsilon)$$
です。

$(\Leftarrow)$の証明

示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon)$$
です。
今、
$$(\forall i\in\mathbb{N}:1\leq i\leq m)(\forall \epsilon_0>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |f_i(\boldsymbol{x})-A_i|<\epsilon_0)$$
が成り立っています。
$\epsilon_0$は任意なので、任意の$\epsilon>0$を用いて$\displaystyle\epsilon_0=\frac{\epsilon}{\sqrt{m}}$としても成り立ちます。
従って、
$$\begin{eqnarray} |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|&=&\sqrt{(f_1(\boldsymbol{x})-A_1)^2+(f_2(\boldsymbol{x})-A_2)^2+\cdots+(f_m(\boldsymbol{x})-A_m)^2}\\ &<&\sqrt{\frac{\epsilon^2}{m}+\frac{\epsilon^2}{m}+\cdots+\frac{\epsilon^2}{m}}\\ &=&\sqrt{m\cdot \frac{\epsilon^2}{m}}\\ &<&\sqrt{\epsilon^2}=\epsilon \end{eqnarray}$$
となります。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in\bar{\Omega}:0\geq |\boldsymbol{x}-\boldsymbol{a}|<\delta\Rightarrow |\boldsymbol{f}(\boldsymbol{x})-\boldsymbol{A}|<\epsilon)$$
です。

証明終わり

従って、

というわけです。
「あまり代わり映えしないネ」と思うかもしれません。
形式的にはそうです。
しかし、この定理は強力ではありますが、関数値が実数からベクトルになること自体に難しさが無いと述べているに過ぎません。
多変数ベクトル値関数は点列と違い、定義域の次元も変わってしまいますので注意が必要です。
これについては別の記事を書きます。

ちょっと踏み込んだ多変数ベクトル値関数の収束のイメージ

実は点列と同じ部分もあれば違う部分もあります。
どの場合で違うかというと、終域によってイメージが変わってきます。
つまり、

• 実数値関数
• ベクトル値関数

の２つの場合でそれぞれイメージが違います。

多変数実数値関数の場合

これは点列と数列との違いと同じです。
「極限への近づき方が多次元的だ」ということが違いです。

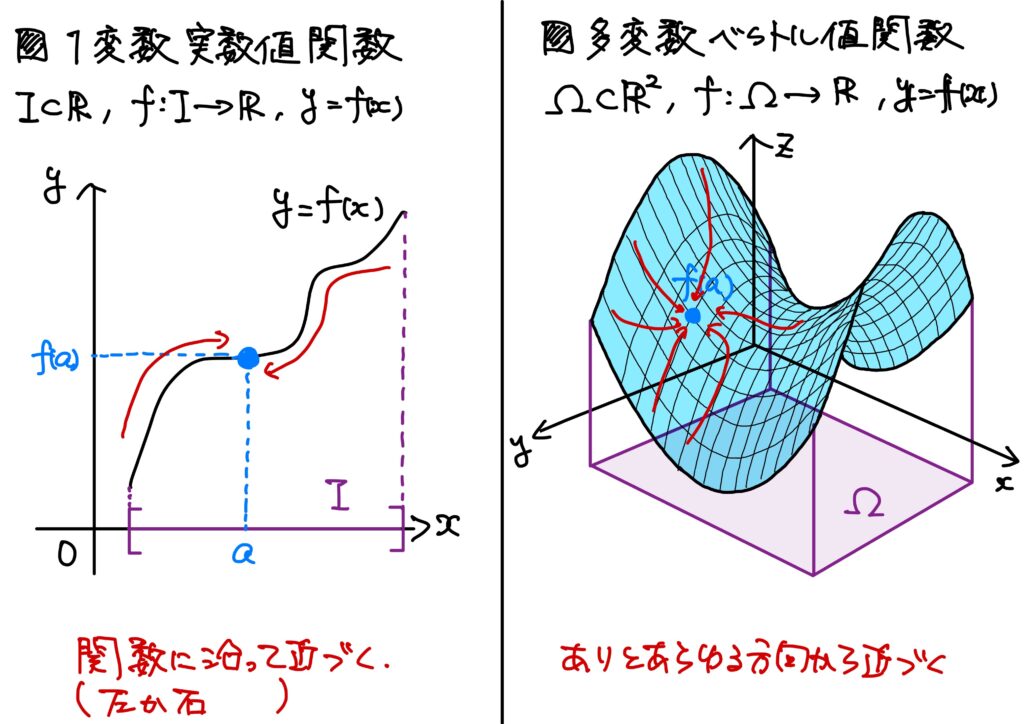
1変数実数値関数の極限への近づき方は関数に沿って近づく、そういう意味では1次元的でした。
一方多変数実数値関数の近づき方は多次元的です。
つまり、ありとあらゆる方向から近づきます。

多変数ベクトル値関数の場合

これはイメージが難しいです。
というのも、極限がベクトルだからです。
「ベクトルに収束するってのはどういうことかね？」となっちゃうので難しいです。
定義域と終域が3次元だったとしてもグラフは描けません。

サラっとではありますが、グラフについて述べることにします。

グラフって？

「グラフとは何かネ？」と聞かれたらば「関数のグラフであれば、集合です。」が答えです。
(※広義には点と点との繋がりにのみ着目したグラフ理論という分野もあるので、ひとえにグラフは集合です、とは言い切れません。)
実は数学では関数のグラフは図ではなく、集合です。
よく言う「関数のグラフ」は、グラフと呼ばれる集合を図示したもので、グラフそのものではありません。

例1. $f:[0,1]\to\mathbb{R}$が$f(x)=x^2$で定められているとしましょう。
このとき$f$のグラフ$G(f)$は
$$G(f)=\{(x,y)\in I\times\mathbb{R}\mid y=x^2\}$$
です。
つまり、定義域と終域の直積集合の部分集合です。
さらに言えば、$G(f)\subset \mathbb{R}^2$です。
それ故、図が描けます。

一般に、グラフというのは次を指します。

多変数ベクトル値関数の場合は図が描けないこともしばしばあります。
というのも、次を考えてみましょう。

例2. $\boldsymbol{f}:\mathbb{R}^2\to\mathbb{R}^2$が
$$\boldsymbol{f}(\boldsymbol{x})=\left( \begin{array}{c} x+y \\ x-y\\ \end{array}\right)$$
で定められているとしましょう。
このとき$\boldsymbol{f}$のグラフは
$$\begin{eqnarray} G(f)&=&\{(\boldsymbol{x},\boldsymbol{y})\in \mathbb{R}^2\times \mathbb{R}^2\mid \boldsymbol{y}=\boldsymbol{f}(\boldsymbol{x})\}\\ &=&\left\{(x_1,x_2,y_1,y_2)\in \mathbb{R}^4\middle| \left( \begin{array}{c} y_1\\ y_2\\ \end{array}\right) =\boldsymbol{f}\left( \begin{array}{c} x_1\\ x_2\\ \end{array}\right)\right\} \end{eqnarray}$$
となり、4次元ですのでグラフを図に描くことはできません。
定義域と終域が2次元でもこのようなことが起こります。
従って、多変数ベクトル値関数の図を描くことはできないことが多いです。

では、何も描けないのかネ？

いえ、そんなことはありません。
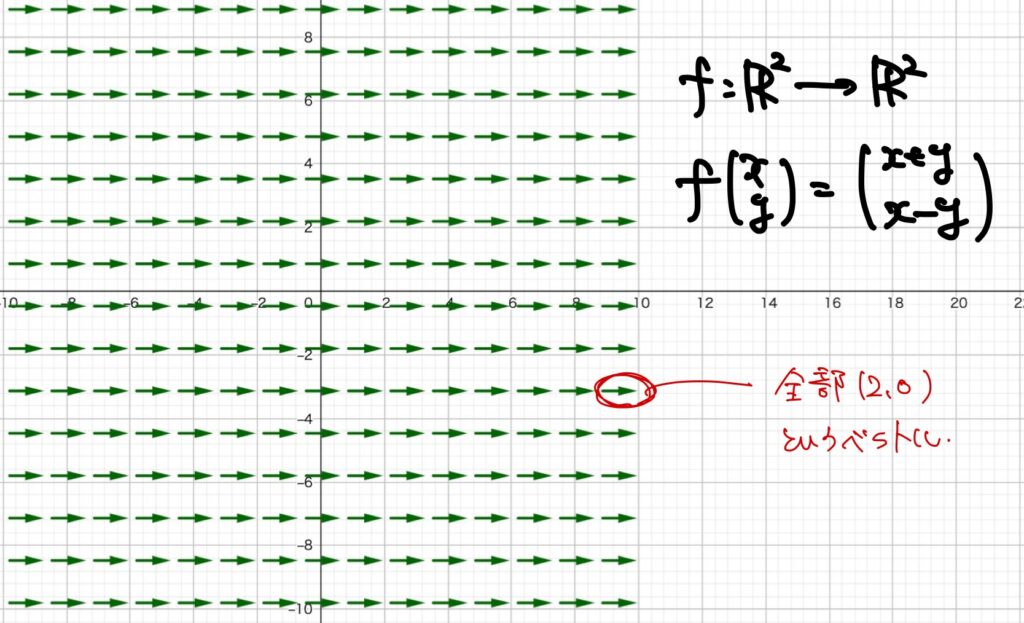
例2.を別の視点で見てみましょう。
すると、例2.の$\boldsymbol{f}$はベクトルに対してベクトルを対応させる関数です。
つまり、$(x,y)$という座標に対して、$(x+y,x-y)$というベクトルを対応させていると考えることができます。
例えば、$(1,2)$という座標に対しては$(3,-1)$というベクトルを対応させているわけです。
従って、次のような図を描くことができます。

多変数ベクトル値関数の収束のイメージは、このいっぱいある矢印が全て同じ方向と大きさの矢印になることです。
図としてはこんな感じになります。

実際に証明してみよう！

では、実際に証明してみましょう。
先程挙げた例2.を証明してみましょう。

例2. $\boldsymbol{f}:\mathbb{R}^2\to\mathbb{R}^2$が
$$\boldsymbol{f}(\boldsymbol{x})=\left( \begin{array}{c} x+y \\ x-y\\ \end{array}\right)$$
で定められているとします。
このとき、
$$\lim_{\boldsymbol{x}\to(1,1)} \left(\begin{array}{c} x+y\\ x-y\\ \end{array}\right)=\left(\begin{array}{c} 2\\ 0\\ \end{array}\right)$$
です。

証明

示したいことは
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall (x,y)\in\mathbb{R}^2\\ 0<\sqrt{(x-1)^2+(y-1)^2}<\delta\Rightarrow \sqrt{(x+y-2)^2+(x-y)^2}<\epsilon\right)$$
です。
$\delta>0$を見つけるために、$\sqrt{(x+y-2)^2+(x-y)^2}$を変形します。
$$\begin{eqnarray} \sqrt{(x+y-2)^2+(x-y)^2}&=&\sqrt{x^2+2xy+y^2-4(x+y)+4+x^2-2xy+y^2}\\ &=&\sqrt{2x^2+2y^2-4x-4y}\\ &=&\sqrt{2}\cdot\sqrt{x^2-2x+y^2-2y}\\ &=&\sqrt{2}\cdot\sqrt{(x-1)^2+(y-1)^2-2}\\ &<&\sqrt{2}\cdot\sqrt{(x-1)^2+(y-1)^2}\\ \end{eqnarray}$$
従って、任意の$\epsilon>0$に対して$\displaystyle\delta=\frac{\epsilon}{\sqrt{2}}$とすれば、
$$\begin{eqnarray} \sqrt{(x+y-2)^2+(x-y)^2}&<&\sqrt{2}\cdot\sqrt{(x-1)^2+(y-1)^2}\\ &<&\sqrt{2}\cdot\delta\\ &<&\sqrt{2}\cdot\frac{\epsilon}{\sqrt{2}}\\ &=&\epsilon \end{eqnarray}$$
となります。
従って、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ \left(\forall (x,y)\in\mathbb{R}^2\\ 0<\sqrt{(x-1)^2+(y-1)^2}<\delta\Rightarrow \sqrt{(x+y-2)^2+(x-y)^2}<\epsilon\right)$$
です。

結

今回は多変数ベクトル値関数の極限について説明しました。
多変数ベクトル値関数の極限は1変数実数値関数と形式的にはほとんど同じですが、近づき方幾通りもあるという点で違いがあるのでした。

ただ、点列と同じなのは、各成分ごとに極限を考えればOKという点です。

若干余談ながら、グラフの話もしました。
実はグラフは図ではなく集合です。
多変数ベクトル値関数は定義域と終域が2次元や3次元だったとしてもグラフ自体は4次元、6次元ですのでグラフを描くことはできません。
しかし、座標に対してベクトルを対応させる関数が多変数ベクトル値関数なので、各座標にどんなベクトルが対応しているかを描くことはできます。

次回は多変数ベクトル値関数の和、差の極限について解説します。

乞うご期待！質問、コメントなどお待ちしております！