数列の収束って？〜直感から論理へ〜

本記事の内容

本記事は「有界な単調列は収束する」という命題の証明に必要な、数列の極限を説明する記事です。

この記事を読むにあたり、数列とはどういうものかを知っている必要があるため、以下の記事も合わせて御覧ください。

数列？　有界？　単調列？

...

for-spring.com

2022.03.07

収束の直感的なイメージとその例

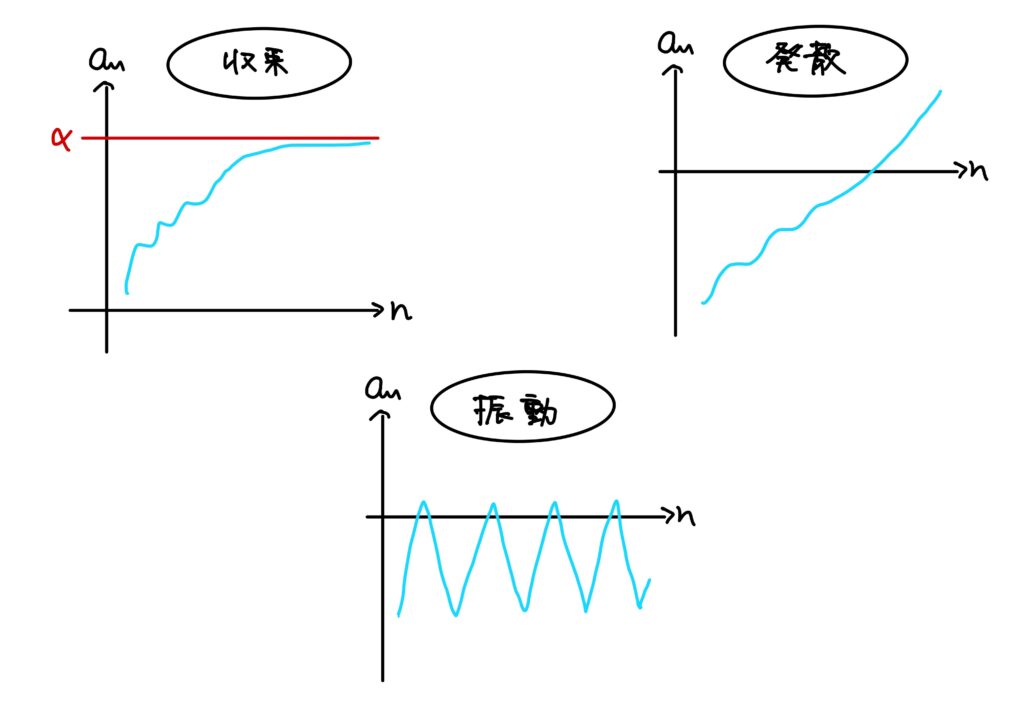
「収束」の直感的なイメージは、「項の番号$n$が限りなく大きくなっていくとき、ある一定の値に限りなく近づいていくならば、収束する、という。」ということです。
要は数列$\{a_n\}$の項の番号$n$を大きくしていったとき、$\{a_n\}_{n\in\mathbb{N}}$がある値$\alpha$に行き着くならば、その行き着いた$\alpha$を数列$\{a_n\}{n\in\mathbb{N}}$の極限といい$\displaystyle\lim_{n\to\infty}a_n$と書きます。
またこのとき、$\{a_n\}_{n\in\mathbb{N}}$は収束するといいます。
ちなみに、収束せずに$a_n$の値がどんどん大きくなっていくときは発散するといい、収束せず$\{a_n\}$の値がギザギザと波打っていくときは振動するといいます。
発散するとき、$\displaystyle\lim_{n\to\infty}a_n=\infty$と書きます。

直感から論理(数学)へ

さて、「収束する」ということの直感的なイメージは湧きやすいと思うので、いよいよ「限りなく」という文言を、特に「限りなく近づく」、「限りなく大きくなる」という文言を論理的に厳密に書くとどうなるかという話をしましょう。

限りなく近づく

「近づく」という言葉を使うときを思い出してみます。
すると、モノ同士が近づく、という表現で使われる事が多いように感じます。
少々昔の話になるのだが、とあるお笑い芸人に「1日2ミリバス停ずらす！すごい2年を費やし自宅の前へ！」という「そんなことをしちゃうあっちゃんカッコいい！」というネタがあります。
これは何が近づくの？と言われれば自宅とバス停であるが、より正確には自宅とバス停の”距離”が近づくのです。
したがって、”限りなく近づく”の近づくは”距離”によって表現できます。

さて、実数の数直線において”距離”は何で表現されるでしょうか。
それは「絶対値」です。
特に、二点の値の差の絶対値です。　
すなわち、実数$a$と実数$b$の距離は$\mid a-b \mid=\mid b-a \mid$で表現されます。
実際、$1$と$7$の距離は$\mid 1-7\mid=\mid 7-1\mid=6$です。
また、$-2$と$5$の距離は$\mid -2-5\mid=\mid 5-(-2)\mid=7$です。
従って、”近づく”という文言は$2$点間の距離が小さくなることを指すわけです。

では”限りなく近づく”を考えてみます。
今の段階で”限りなく近づく”を言い換えてみると、”限りなく$2$点$a,b\in\mathbb{R}$間の距離が小さくなる”となります。
そもそも距離はどれくらい離れているかの指標なのだから負の値は取りません。
すなわち$0$以上の値を取ります。(そもそも絶対値は必ず$0$以上の値を取ります。)
“限りなく”距離が小さくなるのだから$\mid a-b\mid$の値がめちゃくちゃ小さくなるということです。
すなわち、この”めちゃくちゃ小さくなる”ということを数学で表現できれば良いわけです。
これを数学で表現すると、「どんな正の実数よりも$2$点間の距離が小さい」となるのです。
つまり、どんな$0$と距離近い数(どんなに$0$の近くの正の実数)を取ってきたとしても、かならず$2$点の間の距離はその正の数よりも小さい、と表現できるわけです。
より端的に言えば、「$2$点の距離がどんな正の実数よりも小さい」というのが”限りなく近づく”ということなのです。
「そんな$0$と近い実数なんてあるんすか？」となるかもしれないが、これは存在します。
というのも、我々はワイエルシュトラスの上限公理を仮定しているので、実数の連続性は担保されているのだから、$0$にもその十分近くにまた実数があるのです。

これを論理式で表してみると、以下です。

限りなく大きくなる

「”限りなく大きくなる”という文言もさっきと同じ感じなのかな？」と思うかもしれませんが、実は少々違います。
というのも、”近づく”という文言は距離が$0$より小さくはならないというある種の基準があった一方で、”大きくなる”は際限がないからです。
そもそも数列の各項に対する番号$n$は自然数なのだから、$1$ずつ際限なく大きくなってきます。
故に”限りなく大きくなる”ということは特に自然数について考えるということですでに担保されています。

数列って段々と極限に近づいていくよね？

そのとおりである、と言い切ると若干語弊があるのですが、おおよそそのとおりです。
というのも、ギザギザしながらだんだんと極限に近づいていくような数列も存在するからです。

とどのつまり、初項からいきなり極限\(\alpha\(に近いわけではなく、番号をどんどん大きくすることによって段々と近づいていく。
実際、例2.を見てみましょう。

例2.(反比例に似た数列)
$\displaystyle a_n=\frac{1}{n}$の初項$1$と極限$0$は$\epsilon=\displaystyle\frac{1}{4}$に対して$\displaystyle\mid1-0\mid>\frac{1}{4}$です。
従って、どんな正の実数$\epsilon$に対しても極限との距離が$\epsilon$よりも小さいくなければ近づいたとは言えないので、$1$と$0$は近くない。

すなわち、段々と近づく、という”段々と”を数学的に言えれば良いわけです。
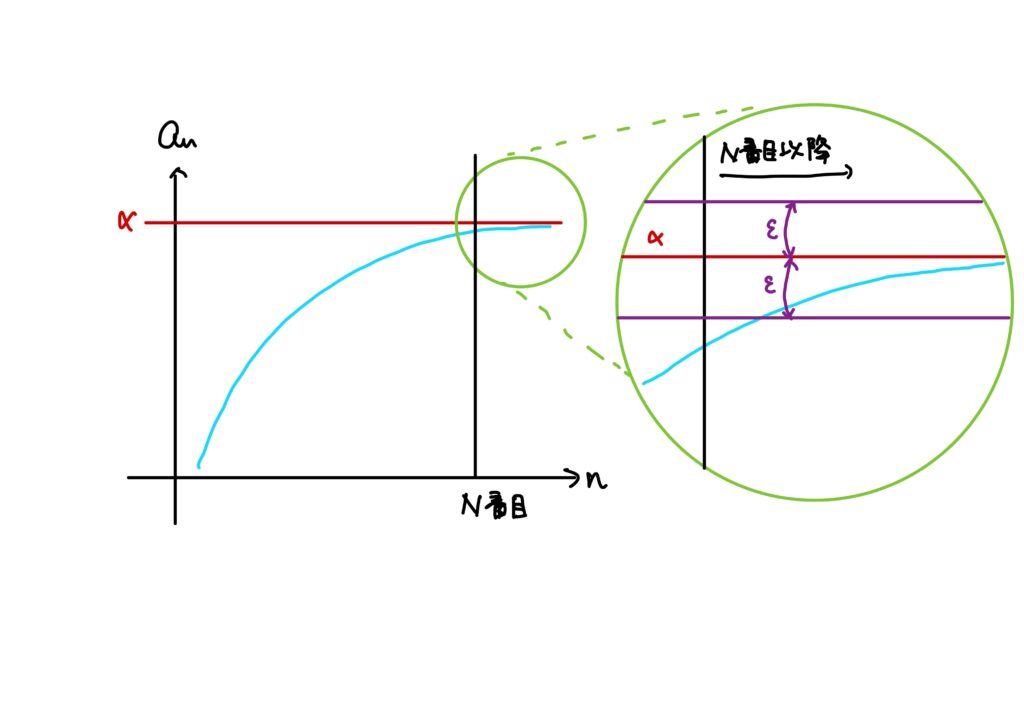
これは「とある番号$N$以降の番号に対して」と表現するのです。
これは若干”段々と”という文言と差があるかもしれないのだが、”近い”の数学的表現とともに使うことでしっくり来ると思われます。
つまり、「数列のとある番号$N$以降の項は全て極限との距離がどんな正の実数よりも小さい」と表現することで、”段々と”と”限りなく近づく”を表現できるわけです。
ここで注意なのが、このとある番号$N$はどんな数列に対しても適用できるような絶対的な値ではないということです。
各数列に特に任意の正の実数$\epsilon$に依存する値です。

以上のことをまとめると、数列$\{a_n\}_{n\in\mathbb{N}}$が$\alpha$に収束するというのは、

数列の収束

上記の数列の収束を論理式で書けば、次です。

これをもう一度日本語でかくと、

である。
故に、ある数列$\{a_n\}_{n\in\mathbb{N}}$が収束することを示しなさいと言われたらば、上記を満たすようなとある番号$N$($N$番目以降の$a_n$は極限と近いような番号$N$)を見つけてきなさい、ということです。

数列が収束することを証明してみよう

例2.の$\displaystyle\frac{1}{n}$としたときの数列$\{a_n\}_{n\in\mathbb{N}}$が極限$0$に収束することを証明してみましょう。

筆者の個人的な感覚なのだが、数列の収束の証明の理解が解析学の理解への登竜門だと感じます。
それは、筆者の感覚だと、数学を直感から切り離し、論理の世界に入るその瞬間が数列の収束の証明だと感じるからです。
実際、筆者の大学の同級生にもこの数列の収束(通称$\epsilon-N$論法)の理解に苦しむ人がいました。(筆者もその１人だったのだけれどね。)
このことから、やはり難しいのです。
しかし、そこで投げ出すのではなく、根気強く考え続けることによってあるとき突然理解ができる、と思います。
筆者を数学徒と言っていいのかはおいておいて、少なくとも数学を勉強するにあたり、理解するにあたり根気が必要になってくると思います。
（筆者も「なんだよ！わかんねえよ！」と幾度投げ出そうと思ったか分かりません。とはいえ、やはり数学が好きだったからでしょうが、修士号を取るまで続けました。）

さてさて、筆者の個人的な感想は置いておいて、早速証明に入って行きましょう。
言わずもがな証明はなるべく丁寧に書くつもりです。
その証明の後に、少々また感想を述べることにします。
※この感想は内容としては全く関係ないので、「貴様は偉そうに語っているがどう思ってるんだ？」とちょっと疑問に思った方は是非一読してみてください。

命題4.
$\displaystyle \lim_{n\to\infty}\frac{1}{n}=0.$
※「証明に挑戦してみようかな」という方は下記の証明を読む前に是非一度証明に挑んでほしい！
（ヒント：アルキメデスの原理を使います。下記参照）

証明

以下を示せば良いです。
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left| \frac{1}{n}-0\right|<\epsilon)\cdots①$$
日本語に直すと、

ことを示せばよいわけです。
すなわち、任意の正の実数$\epsilon$に対して、上記を満たすような番号$N\in\mathbb{N}$を見つければ良いわけです。
アルキメデス(アルキメデス)の原理を用います。

アルキメデスの原理はどんな2つの正の実数$a,b$に対しても、$b<N_0a$を満たすような自然数$N_0$が取れます（見つけてくることができます）、という主張なのであるから、$b=1$としても成り立ちます。
すなわち、
$$(\forall a\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ 1<N_0a$$
が成り立ちます。

このときの$a$を名前を変えて$\epsilon$と書き直すと、
$$(\forall \epsilon\in\mathbb{R}_{>0})(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ 1<N_0\epsilon$$
さらに、$\epsilon\in\mathbb{R}_{>0}$なのだから、
$$(\forall \epsilon>0)(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ 1<N_0\epsilon$$
です。
すなわち、
$$(\forall \epsilon>0)(\exists N_0\in\mathbb{N})\ {\rm s.t.}\ \frac{1}{N_0}<\epsilon$$
です。
要は、上記を満たすような自然数$N_0$を見つけることができます。
さて、証明したいことは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left| \frac{1}{n}-0\right|<\epsilon)$$
でした。
つまり、任意の実数$\epsilon$に対して、ある番号$N$が存在して、自然数$n$が$n\geq N$ならば、$\left|\frac{1}{n}-0\right|<\epsilon$を満たすことです。
さらにいえば、これを満たすような自然数$N$を見つけてくれば良いわけです。
この$N$として、先程見つけた$N_0$を採用します($N=N_0$とします)。
このとき、この$N$($N_0$のこと)に対して、
$$(\forall n\in\mathbb{N})(n\geq N\Rightarrow \left|\frac{1}{n}-0\right|<\epsilon)$$
が成り立てば証明完了です。
実際、今
$$(\forall \epsilon>0)(\exists N\in\mathbb{N})\ {\rm s.t.}\ \frac{1}{N}<\epsilon\cdots②$$
が成り立っているので、この任意の正の実数$\epsilon$に対して
$$(\forall n\in\mathbb{N})(n\geq N\Rightarrow \left|\frac{1}{n}-0\right|<\epsilon)$$
が成り立てば、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow \left| \frac{1}{n}-0\right|<\epsilon)$$
が成り立つことになります。
さて、$n\geq N$のとき、$\displaystyle\frac{1}{n}\leq\frac{1}{N}$であり、また②により、
$$\left|\frac{1}{n}-0\right|=\left|\frac{1}{n}\right|=\frac{1}{n}\leq\frac{1}{N}<\epsilon$$
です。
すなわち、任意の正の実数$\epsilon$に対して、ある自然数(番号)$N$として$N_0$を採用すれば、$n\geq N$ならば$\displaystyle\left|\frac{1}{n}-0\right|<\epsilon$が成り立つので、①が証明されました。

証明終わり

余談(筆者の感想)
数学は何か主張を述べるだけではあまり意味はありません。
その証明を与えてこそ意味がある場合が多いです。
「じゃあ未解決問題に意味はないのか？」と思うかもしれないのだが、そんなことはありません。
現在の未解決問題の殆どが「これが分かったら別の大きな事実がわかる！」という意味があります。
加えて、「数多の数学者が歴史上長らく考えたのだが未だ分からない」という研究者としての好奇心をくすぐるものでもあります。
要は、数学の理論の展開において証明は切っても切り離せない存在です。
一見正しそうでも実は正しくない主張がある通り、証明して初めて正しいと言えます。
その証明の中で、筆者が個人的に一番難しいと思う形式の証明は、「とある〇〇が存在する。」という主張の証明です。
その他の証明は別の事実から芋づる式に出てきたり、式変形をしたりすればおおよそ証明ができるのですが、「〇〇が存在する」という主張の証明は、その〇〇を具体的に見つけてこなければならないため、アイデアが必要になるのです。
筆者は「〇〇が存在する」という主張の証明をする際に心がけているのが、「スタートからゴールを目指すのではなく、ゴールからスタートに逆算する」ということです。
「こうなってほしいなあ〜。そのためにはこうなってなきゃいけないなあ〜。だからこういう主張があればいいなあ〜」というようにゴールから考えるのです。
上記の命題を例に取れば、「$\displaystyle \frac{1}{n}<\epsilon$が$\forall\epsilon>0$で成り立ってほしいなあ。この不等式に似てる不等式があればいいんだけどなあ。あ、アルキメデスの原理って似てるよな。考えてみるか。あ、これでいけるじゃん。よっしゃ。」と言った具合です。
最も大事なのは、「あ、アルキメデスの原理って似てるよな。」という発想に至ることです。
そのためには数多くの事実を正確に知る必要があるため、「〇〇が存在する」という主張の証明は難しいのだな、と思います。
同時に、勉強し始めた当初はその知識がまだ少ないため、アイデアも生まれにくいということで難しいのだなあと思います。

結

今回は「有界な単調列は収束する」という命題の証明に必要な数列の極限について解説しました。
高校数学で学んだ極限の直感的な理解から、極限の論理的な理解についての橋渡しに重きをおいたつもりです。

次回は「有界な単調列は収束する？」です。

乞うご期待！質問、コメントなどお待ちしております！