本記事の内容
本記事は多変数バージョンの中間値の定理のイメージを説明する記事です。
本記事を読むにあたり、1変数実数値関数の場合の中間値の定理について知っている必要があるため、その際は以下の記事を参照してください。
1変数実数値関数の場合の中間値の定理のチャラい復習
1変数実数値関数の場合の中間値の定理をチャラく復習します。
一言で述べれば、
ということでした。
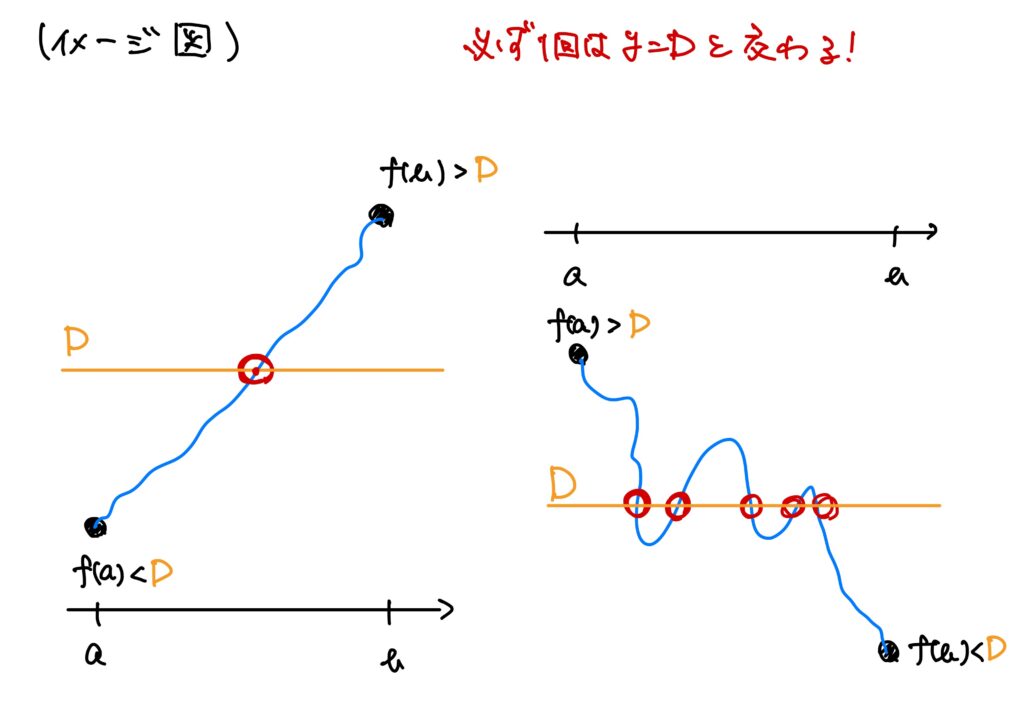
この主張を数学的に明示すると、次でした。

1変数実数値関数の場合は、連続な関数の定義域の端点での関数の値の一方が\(y=D\)より大きく、一方が\(y=D\)より小さいときに、その関数は\(y=D\)という”直線”と必ず交点がある、ということでした。
一方、多変数の場合の中間値の定理は、\(z=D\)という”平面”と必ず交点があるということです。
1変数実数値関数の定義域は区間でした。
「であれば、多変数の場合は単に領域になるだけかネ?」と思うかもしれませんが、そう単純な話ではありません。
ここで、弧状連結集合について解説します。
弧状連結集合
弧状連結な集合は直感的には特に難しいお話ではありません(特に\(\mathbb{R}\)の場合はね)。
直感的には
というわけです。
図で表すと次になります。
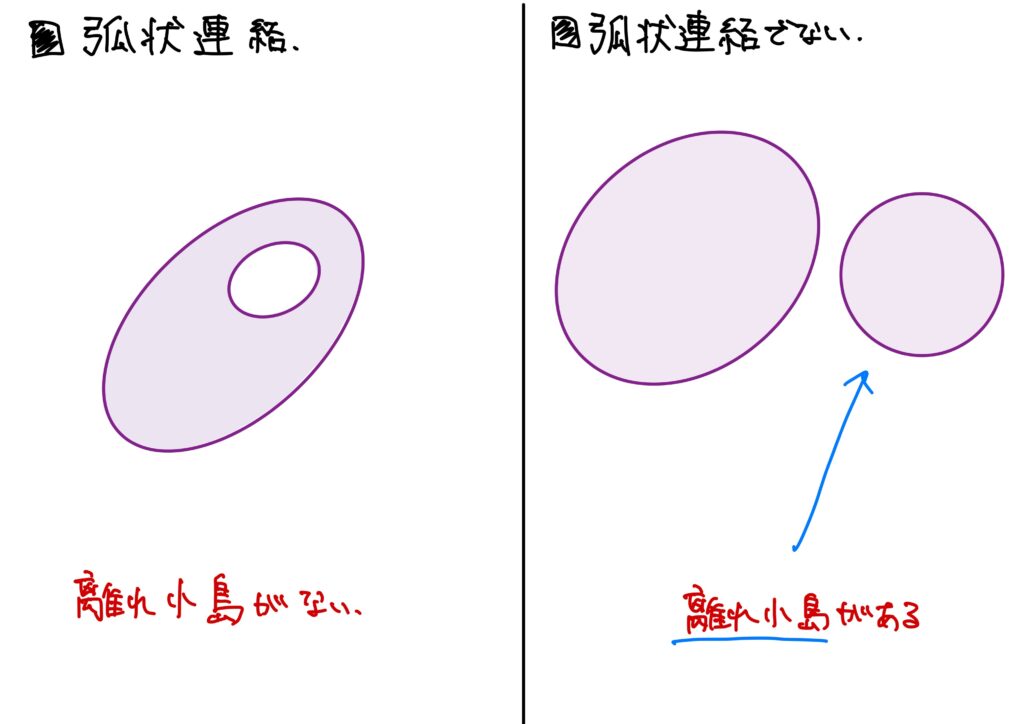
これを数学的に明示すると、次です。

多変数バージョンの中間値の定理のイメージ
多変数バージョンの中間値の定理は言ってしまえば、「直線と交わる」という事が「平面と交わる」に変わるだけです。
ただ、定義域については弧状連結でないといけません(何故かは後述します)。
「で?つまりどういうことかネ?」ということを説明する図が以下になります。
上記の図のように、定義域が弧状連結である(離れ小島が無い)ような連続な多変数実数値関数は必ず\(z=D\)という平面と1回は交わる、ということです。
1変数実数値関数の場合と同様に、連続でない関数については必ずしも\(z=D\)と交わるわけでは有りません。
より直感的な説明
登山を考えてみましょう。

当然のことながら、0合目から登頂するには必ず8合目に到達しなければいけません。
(富士山などはリフトがあったりするようですけどね)
いきなり4合目から、頂上にひとっ飛びというわけには行きません。
この「必ず8合目に到達しなければならない」というのが「\(z=D\)と必ず1回は交わる」ということに対応しています。
余談(本当に読まなくてOK)
数学の論証はよく登山に例えられます。
それが理由なのかは定かでは有りませんが、数学者には登山を趣味とする人が割といます。
かくいう筆者の師匠も登山が趣味でした。
正直なところ、趣味は人それぞれですし貶すつもりは一切ありませんが、筆者は「疲れるからやだな」と思っています(笑)。
弧状連結でなければダメなのかネ?
ダメなんです、局長。
例えばこんな場合があるからです。
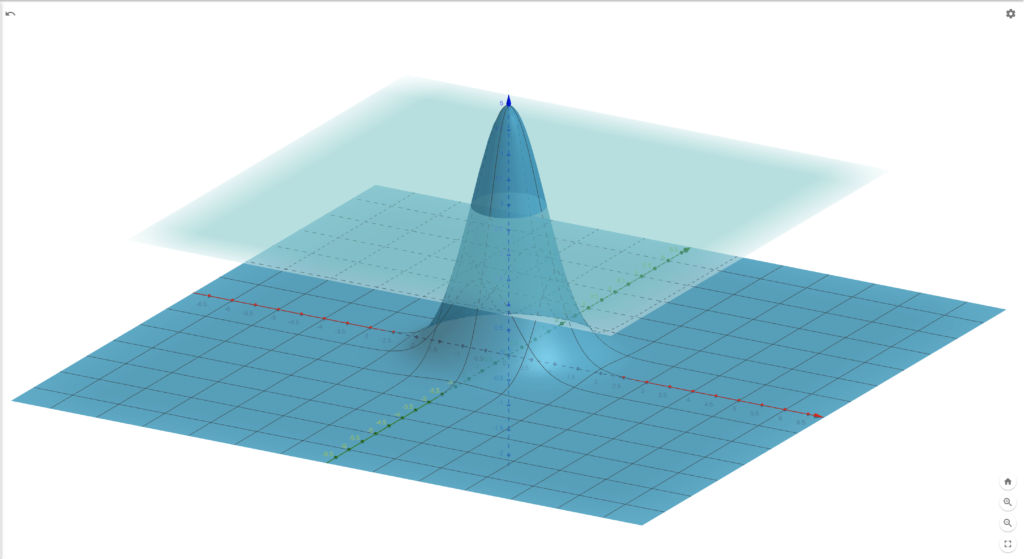
例1. \(\Omega=\{(x,y)\in\mathbb{R}^2\mid x^2+y^2=1\}\cup \{(x,y)\in\mathbb{R}^2\mid (x-2)^2+y^2=1\}\)とします。
また、\(f:\Omega\to\mathbb{R}\)が\(f(x,y)=x^2+y^2\)で定められているとします。
\(f\)は\(\Omega\)で連続ですが、\(\Omega\)は弧状連結ではありません。
このとき、\(f\)のグラフは次です。

\(f\)は\(f(0,0)<5<f(2,1)\)ですが、\(z=1\)とは交わりません。
このように、たとえ定義域で連続な関数であったとしても定義域が弧状連結出ない場合には\(z=D\)と交わらない事があるので、中間値の定理が成り立ちません。
結
今回は多変数の場合の中間値の定理のイメージを解説しました。
イメージとしては、1変数実数値関数の場合が\(y=D\)という直線と必ず1回は交わる、ということだったのに対して、多変数実数値関数の場合は\(z=D\)という平面と必ず1回は交わる、ということでした。
ただ、1変数の場合との違いは定義域です。
多変数の場合は定義域が弧状連結という”離れ小島が無い”ような定義域の関数、という条件が必要なのでした。
次回は多変数の場合の中間値の定理を実際に証明します。
とはいえ、そんなに難しい話ではなく、1変数実数値関数の場合の中間値の定理から、比較的すぐ証明できます。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする