本記事の内容
本記事は部分積分を厳密に証明する記事です。
本記事を読むにあたり、積の微分法と微分積分学の基本定理について知っている必要があるため、以下の記事も合わせてご覧ください。
↓積の微分法の記事
↓微分積分学の基本定理の記事
部分積分は積の微分法に基づいています。
前回(【解析学の基礎シリーズ】積分編 その18)で解説した置換積分(変数変換公式)は、合成関数の微分法に基づいていました。
これに対して、部分積分は積の微分法に基づいています。
少々余談ですが、置換積分、部分積分はそれぞれ合成関数の微分法、積の微分法に基づいているので、このことからも微分と積分は非常に深い関係にあることが見て取れます。
最も微分と積分の深い関係を表しているのは微分積分学の基本定理だとは思いますが。
高校で習った部分積分法の軽い復習
まずは、部分積分がどういう手法だったかということを復習しましょう。
※数Ⅲの内容も含まれますので、数Ⅲを学習していない方は「ふーん。そうなんだー。」でOKです。
例1. \(\displaystyle\int_0^1xe^x\ dx\)を計算します。
\begin{eqnarray}
\int_0^1xe^x\ dx&=&\int_0^1x\left( e^x\right)^\prime\ dx\\
&=&\left[ xe^x\right]_0^1-\int_0^1\left( x\right)^\prime e^x\ dx\\
&=&\left[ e-0\right]-\int_0^1e^x\ dx\\
&=&e-\left[ e^x\right]_0^1\\
&=&e-\left( e-1\right)=1
\end{eqnarray}
という計算方法でした。
部分積分法の明示とその証明
では、まず主張を明示します。
部分積分法の明示
定理2.(部分積分法)
\(I=[a,b]\)を\(\mathbb{R}\)の閉区間とし、\(f:I\to\mathbb{R}\)、\(f^\prime:I\to\mathbb{R}\)、\(g:I\to\mathbb{R}\)、\(g^\prime:I\to\mathbb{R}\)が\(I\)上で可積分(例えば、連続または単調である)とする。このとき、 $$ \int_a^bg^\prime(x)f(x)\ dx=\left[g(x)f(x) \right]_a^b-\int_a^bg(x)f^\prime(x)\ dx\cdots① $$ が成り立つ。特に、\(g(x)=x\)のとき、 $$ \int_a^bf(x)\ dx=\left[xf(x) \right]_a^b-\int_a^bxf^\prime(x)\ dx\cdots② $$ である。
証明は、先程述べた通り積の微分法を用います。
また、証明も誠にシンプルです。
部分積分法の証明
定理2.の証明
まず、積の微分法を使います。
定理3.(積の微分法)
$$\left(f(x)g(x)\right)^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)$$定理3.の証明は【解析学の基礎シリーズ】1変数実数値関数の微分編 その2を御覧ください。
積の微分法から、
$$
\left(f(x)g(x)\right)^\prime=f^\prime(x)g(x)+f(x)g^\prime(x)
$$
が成り立ちます。
仮定から、\(f\)、\(f^\prime\)、\(g\)、\(g^\prime\)が可積分だから、\(f^\prime g\)も\(fg^\prime\)も可積分です。
実際、次が成り立つからです。
定理4.
\(I\subset\mathbb{R}^n\)とする。2つの有界な関数\(f\)、\(g\)が\(I\)上で可積分であれば、積\(fg\)も\(I\)上で可積分である。定理4.の証明は【解析学の基礎シリーズ】積分編 その8を御覧ください。
\(f^\prime g\)も\(fg^\prime\)も可積分なので、\(f^\prime(x)g(x)+f(x)g^\prime(x)\)も可積分です。
実際、次が成り立つからです。
定理1.(積分の線型性)
\(\mathbb{R}^n\)の有界閉区間\(I\)上で可積分な実数値関数全体の集合\(\mathcal{R}(I)\)は実線型空間であり、\(I\)上の積分は\(\mathcal{R}(I)\)から\(\mathbb{R}\)への線型写像である。すなわち、\(\forall f,g\in\mathcal{R}(I)\)、\(\forall c\in\mathbb{R}\)に対して、\(f+g,\ cf\in\mathcal{R}(I)\)であり、かつ- \(\displaystyle\int_I(f+g)(\boldsymbol{x})\ d\boldsymbol{x}=\int_{I}f(\boldsymbol{x})\ d\boldsymbol{x}+\int_{I}g(\boldsymbol{x})\ d\boldsymbol{x}\)
- \(\displaystyle\int_I\left( cf\right)(\boldsymbol{x})\ d\boldsymbol{x}=c\int_If(\boldsymbol{x})\ d\boldsymbol{x}\)
定理5.の証明は【解析学の基礎シリーズ】積分編 その2を御覧ください。
故に、\(\left( fg\right)^\prime\)も可積分です。
そこで、微分積分学の基本定理を使います。
定理0.(微分積分学の基本定理)
\(I\)を\(\mathbb{R}\)の有界閉区間、\(f\)を\(I\)上の実数値関数、すなわち\(f:I\to\mathbb{R}\)とする。このとき以下の2つが成り立つ。- \(f\)が\(I\)で微分可能で、導関数\(f^\prime\)が\(I\)上で可積分(例えば、連続)ならば、任意の\(a,b\in I\)に対して $$ \int_a^bf^\prime(x)\ dx=f(b)-f(a) $$ が成り立つ。
- \(f\)が\(I\)上で可積分で、1点\(x\in I\)で連続ならば、\(f\)の不定積分\(\displaystyle F(x)=\int_a^xf(y)\ dy\)は\(x\)で微分可能で、\(F^\prime(x)=f(x)\)が成り立つ。
定理0.(微分積分学の基本定理)の証明は【解析学の基礎シリーズ】積分編 その14を御覧ください。
定理0.の1.と定理5.から
$$
\int_a^bf^\prime(x)g(x)\ dx+\int_a^bf(x)g^\prime(x)\ dx=\int_a^b\left( f(x)g(x)\right)\ dx=[f(x)g(x)]_a^b
$$
となります。
従って、
$$
\int_a^bg^\prime(x)f(x)\ dx=\left[g(x)f(x) \right]_a^b-\int_a^bg(x)f^\prime(x)\ dx\cdots①
$$
を得ます。
定理2.の証明終わり
不定積分における部分積分法
定理2.において、積分の上端\(b\)を変数\(x\)で置き換えて、定数をまとめて簡単にすれば不定積分に関する部分積分の公式が得られます。
すまわち、\(C\in\mathbb{R}\)を定数として、
$$
\int g^\prime(x)f(x)\ dx=f(x)g(x)-\int g(x)f^\prime(x)\ dx+C\\
\int f(x)\ dx=xf(x)-\int f^\prime(x)\ dx+C\\
$$
が得られます。
部分積分法を使ってみます。
実際に使って計算してみます。
対数関数の原始関数
以前の記事で原始関数を紹介、証明しました。
その中で原始関数は置換積分と部分積分を駆使することで導出することが出来る、と述べました。
ここではその1例を紹介します。
例6. \(\displaystyle\int \log x\ dx\)を計算してみます。
部分積分法を使うと、
\begin{eqnarray}
\int \log x\ dx&=&\int (x)^\prime\log x\ dx\\
&=&(x)\log x-\int x\left( \log x\right)\ dx\\
&=&x\log x-\int x\cdot\frac{1}{x}\ dx\\
&=&x\log x-\int1\ dx\\
&=&x\log x-x+C
\end{eqnarray}
が得られます。
扇形と円の面積
例7.(扇形の面積) \(\displaystyle I=\int_0^x\sqrt{a^2-x^2}\ dx\ (|x|\leq a)\)を計算してみます。
定理2.(部分積分法)により、
\begin{eqnarray}
I&=&\int_0^x\left( x\right)^\prime\sqrt{a^2-x^2}\ dx\\
&=&x\sqrt{a^2-x^2}+\int_0^x\frac{x^2}{\sqrt{a^2-x^2}}\ dx\\
&=&x\sqrt{a^2-x^2}-\int_0^x\frac{-x^2\color{red}{+a^2-a^2}}{\sqrt{a^2-x^2}}\ dx\\
&=&x\sqrt{a^2-x^2}-I+a^2\arcsin\frac{x}{a}
\end{eqnarray}
となります。
最後の等式については、以前の記事で解説した以下の事実を使いました。
命題8.
\(\displaystyle f(x)=\frac{1}{\sqrt{a^2-x^2}}\ (a\neq0)\)の原始関数\(\displaystyle F(x)=\int f(x)\ dx\)は $$ F(x)=\arcsin \frac{x}{a} $$ である。命題8.の証明は【解析学の基礎シリーズ】積分編 その16を御覧ください。
従って、
\begin{eqnarray}
I=x\sqrt{a^2-x^2}-I+a^2\arcsin\frac{x}{a}&\Longleftrightarrow&2I=x\sqrt{a^2-x^2}-a^2\arcsin\frac{x}{a}\\
&\Longleftrightarrow&I=\frac{1}{2}\left(x\sqrt{a^2-x^2}-a^2\arcsin\frac{x}{a}\right)\\
\end{eqnarray}
となります。
この積分の幾何学的意味を考えてみます。
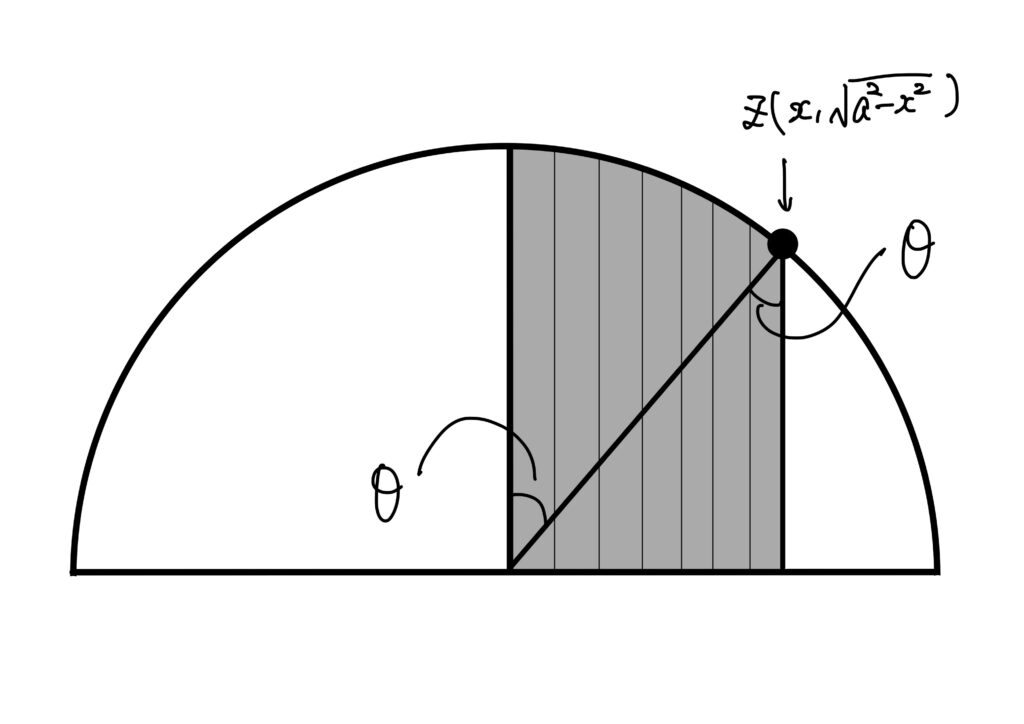
\(\displaystyle\frac{1}{2}x\sqrt{a^2-x^2}\)は図の三角形\(Oxz\)の面積です。
そこで、\(\displaystyle\frac{a^2}{2}\arcsin\frac{x}{a}\)がのことに扇形の面積です。
\(\displaystyle\arcsin\frac{x}{a}=\theta\)は図の角を表すから、
$$
I=\frac{1}{2}\left(x\sqrt{a^2-x^2}-a^2\arcsin\frac{x}{a}\right)
$$
は
を指していると分かります。
高校(もしくは中学校)で習った扇形の面積の公式がここで分かった、ということになります。
ちなみに、これは図のような特定の位置にある扇形に対して成り立つということを証明したわけですが、図形は回転しても面積が変わらないので、任意の扇形の面積に対して成り立つことが分かります。
特に、\(x=a\)とすると、四分円(四分割された円)の面積が\(\displaystyle\frac{\pi^2}{4}a^2\)を得ることができるので、円の面積は\(\pi a^2\)だ、ということも分かります。
皆様のコメントを下さい!
以前にも同様のことを皆様にお聞きしましたが、改めてお聞きしたいです。
何をか、というと、「中学、高校の数学で何処まで厳密な話をするか。」ということです。
大学で学ぶ厳密な数学をそのまま中学や高校で学ぶのは難しいと思います。
では、「直感的な理解で良いところと、厳密な話をするところ」を分ける基準は一体何処にあるのでしょうか。
これのイメージが付くと、数学が苦手な方のためになるのではないかと思います。
是非皆様の考えをお聞かせ下さい!
結
今回は、部分積分について解説しました。
部分積分も微分積分学の基本定理から得られます。
前回解説した置換積分は合成関数の微分法と関連していたのに対し、部分積分は積の微分法としています。
次回は、1時間チャレンジです!
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください!
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ1冊持っておくと良いと思います!





コメントをする