「多項式関数と有理関数は連続」「連続関数の合成関数も連続関数」「関数の発散」【解析学の基礎シリーズ】関数の極限編 関数の極限を理解する　まとめ③

本記事の内容

本記事は多項式関数と有理関数の連続性、連続関数の合成関数もまた連続関数であること、関数の発散について解説する記事である。
本記事を読むに当たり、関数の連続および数列の発散を知っていると理解が深まると思われるので、その際は以下の記事を参照してください。

関数の連続のリンク貼る

「"数列の発散"って数学的に何？」「$\infty$って数なの？」【解析学の基礎シリーズ】数列の発散編 その2

...

for-spring.com

2022.03.30

序

多項式関数と有理関数は実はすでに知っている。
というのも、多項式関数は$y=x^2+2x+2$のような関数であり、有理関数は$\displaystyle y=\frac{3}{x}$のうような関数だからである。
これらのような関数は数学の世界ではそれぞれ多項式関数、有理関数と呼ばれる。(単に仰々しく言っただけのようなもん)
これらは定義域で連続である。
連続関数の合成関数もまた連続関数である。
つまり、連続関数をうまく”組み立てた”関数もまた連続関数だ、ということである。

数列と同様に、関数にも発散という概念がある。
実際、数Ⅲ(今は呼び名が違うかもしれない。一般的な高３理系が学ぶ数学のこと)$y=x^2$は発散すると習っているはずである。

多項式関数と有理関数は連続

多項式関数

序でのべた$y=x^2+2x+2$ような関数のことを多項式関数という。
「まあ、雰囲気は分かるよ」という感じだと思われるので、早速「多項式関数とは何か？」ということについて述べてしまう。

ちなみに整数係数多項式と言われると、$x^3+4x^2+3$のような式である。
$\pi x^2$というのも許すというのが実係数多項式である。
勿論、整数係数多項式は実係数多項式である。

この多項式関数は連続である。
「本当かよ」と思うかもしれないので、簡単ではあるが、2つの例を挙げる。

(※実は前回すでに証明しているので、「それ知ってる」という方は読み飛ばしてください。)

例1.
$f:\mathbb{R}\to\mathbb{R}$が$f(x)=2x$で定められているとする。
このとき、$f$は$\mathbb{R}$で連続である。

(証明)
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。 つまり、任意の$\epsilon>0$に対して上記を満たすような$\delta>0$を見つけてきなさい、ということである。
$\delta=\frac{\epsilon}{2}$とすると、$\delta>0$である。
$0<|x-a|<\delta$を満たす$x\in\mathbb{R}$に対して、
$$|2x-2a|=2|x-a|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
が成り立ったので、$f$は$\mathbb{R}$で連続である。
(Q.E.D.)

例2.
$g:\mathbb{R}\to\mathbb{R}$が$g(x)=x^2$で定められているとする。
このとき、$g$は$\mathbb{R}$で連続である。

(証明)
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
である。
つまり、任意の$\epsilon>0$に対して上記を満たすような$\delta>0$を見つけてきなさい、ということである。
$\delta=-|a|+\sqrt{|a|^2+\epsilon}$とすると、$\delta>0$である。
$0<|x-a|<\delta$を満たす$x\in\mathbb{R}$に対して、
$$\begin{eqnarray} |x^2-a^2|&=&|(x+a)(x-a)|\\ &=&|x-a+2a|\cdot|x-a|\leq |x-a|^2+2|a|\cdot|x-a|\\ &=&|a|^2-2|a|\sqrt{|a|^2+\epsilon}+|a^2|+\epsilon+2|a|(-|a|+\sqrt{|a|^2+\epsilon})\\ &=&2|a|^2-2|a|^2+2|a|\sqrt{|a|^2+\epsilon}-2|a|\sqrt{|a|^2+\epsilon}+\epsilon=\epsilon \end{eqnarray}$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I\ 0<|x-a|<\delta\Rightarrow |x^2-a^2|<\epsilon)$$
が成り立ったので、$f$は$\mathbb{R}$で連続である。
(Q.E.D.)

例に挙げた通り、多項式関数は連続である。
すなわち、次が成り立つ。

実は、この命題の証明は関数の和・差・積・商の連続性を使うことですぐ終わる。
関数の和・差・積・商の連続性は次であった。

これと「恒等写像は連続である。」、「定数関数は連続である。」という事実を使えば、すぐに終わる。
教科書を書くレベルならものの3行で終わるほどである。
しかし、本記事はなるべく丁寧にをモットーの１つとしているので、少々長くなるが。
(くどいと言われてしまうかもしれないネ)

(命題3.の証明)
$f:\mathbb{R}\to\mathbb{R}$を多項式関数とする。
すなわち、
$$f(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_2x^2+a_1x+a_0\quad(n\in\mathbb{N}\cup\{0\},\ a_i\in\mathbb{R})$$
とする。
次の2つの事実を使う。

(命題4.の証明)
$g:\mathbb{R}\to\mathbb{R}$を恒等写像、すなわち任意の$x\in\mathbb{R}$に対して、$g(x)=x$とする。
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |g(x)-a|<\epsilon)$$
である。
つまり、上記を満たす$\delta>0$を見つけてくれば良い。
$\delta$として任意の正数$\epsilon$を採用する。
$a\in\mathbb{R}$のとき、$0<|x-a|<\delta$なる$x\in\mathbb{R}$に対して、
$$|g(x)-a|=|x-a|<\delta=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-a|<\epsilon)$$
が成り立ったため、恒等写像は$\mathbb{R}$で連続である。
(Q.E.D.)

(命題5.の証明)
$h:\mathbb{R}\to\mathbb{R}$を定数関数、すなわち任意の$x\in\mathbb{R}$に対して、$h(x)=c\ (c\in\mathbb{R})$とする。
示したいことは
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-c|<\epsilon)$$
である。
つまり、上記を満たす$\delta>0$を見つけてくれば良い。
$\delta$として任意の正数$\epsilon$を採用する。
$a\in\mathbb{R}$のとき、$0<|x-a|<\delta$なる$x\in\mathbb{R}$に対して、
$$|g(x)-c|=|c-c|=0<\delta=\epsilon$$
が成り立つ。
従って、
$$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}\ 0<|x-a|<\delta\Rightarrow |h(x)-c|<\epsilon)$$
が成り立ったため、定数関数は$\mathbb{R}$で連続である。
(Q.E.D.)

命題3.の証明に戻る。
命題4.と連続関数の和・差・積・商の3.により、$f_1(x)=a_1x\ (\forall a_1\in\mathbb{R})$で定められる関数$f_1:\mathbb{R}\to\mathbb{R}$は$\mathbb{R}$で連続である。
同様に、$f_2(x)=a_2x^2\ (a_2\in\mathbb{R})$で定められる関数$f_2:\mathbb{R}\to\mathbb{R}$も$\mathbb{R}$で連続である。
この操作を繰り返し行うことによって、任意の$n\in\mathbb{N}\cup\{0\}$に対して、$f_n(x)=a_nx^n$で定められる$f_n:\mathbb{R}\to\mathbb{R}$は$\mathbb{R}$で連続であることが分かる。
ここで、連続関数の和・差・積・商の1.により、連続関数は和をとっても連続であるので、$f_0(x)+f_1(x)+\cdots+f_n(x)+f_n(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots +a_2x^2+a_1x+a_0$もまた$\mathbb{R}$で連続である。
従って、多項式関数は$\mathbb{R}$で連続である。
(Q.E.D.)

命題4.と命題5.の証明も与えたという意味で長くなってしまったけど、命題3.の証明自体はすぐ終わった。
勿論、連続関数の和・差・積・商の事実を用いなくても証明は可能である。
とはいえ、結構骨は折れる。

有理関数

多項式関数がわかれば、有理関数もすぐ分かる。
というのも、平たく言えば、有理関数というのは分母分子が共に多項式関数であるような関数のことを指すからである。
しかし、注意が必要である。
というのも、「分母は$0$でない」という条件が必要だからである。

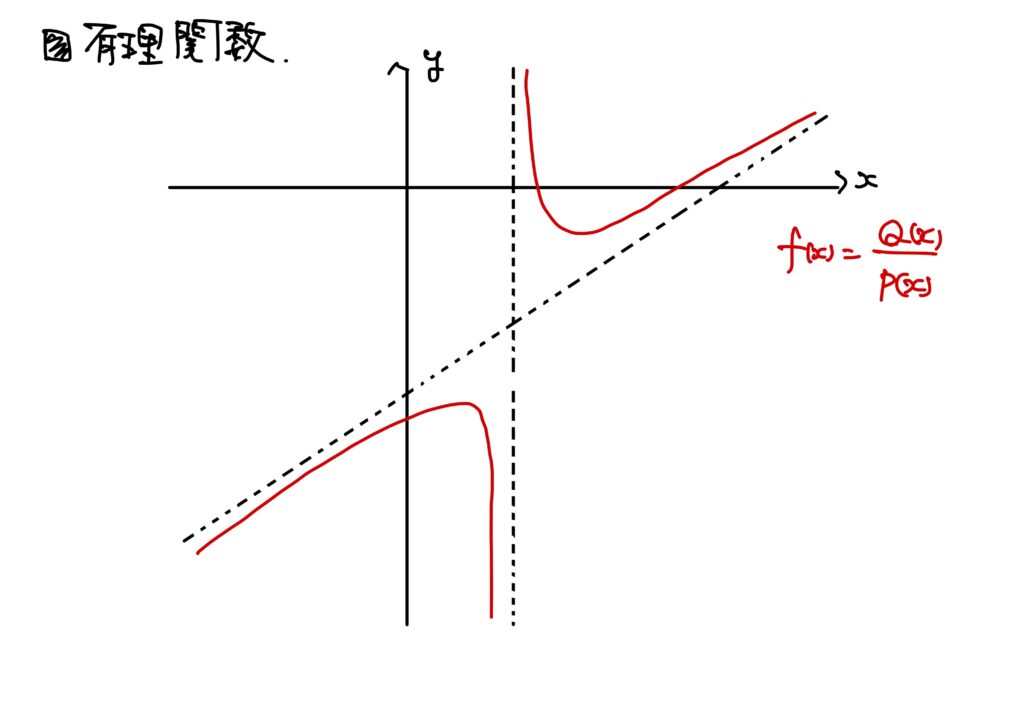
この有理関数は連続である。
「本当かよ」と思うかもしれないので、簡単ではあるが、例を挙げる。

例6. $f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$が$f(x)=\dfrac{x^2-2x+1}{2x}$で定められているとする。
このとき、$f$は$\mathbb{R}\setminus\{0\}$で連続である。

このように有理関数は連続である。
すなわち、次が成り立つ。

(証明)
これも、関数の和・差・積・商の商の事実から直ちに証明できる。

$f:\mathbb{R}\to\mathbb{R}$を有理関数とする。
このとき、$f$は多項式関数$P(x)\neq0$と$Q(x)$を用いて、$f(x)=\dfrac{Q(x)}{P(x)}$と書ける。
$P(x)$と$Q(x)$は多項式関数なのだから、$\mathbb{R}$で連続である。
従って、連続関数の商から$f$は$\{x\in\mathbb{R}\mid P(x)\neq 0\}$で連続である。
(Q.E.D.)

これまでのことをまとめて、

連続関数の合成関数も連続関数

連続関数の合成関数もまた連続関数なのである。
「これが分かると何が嬉しいの？」と思われるかもしれないが、筆者が挙げる例は比較的分かりやすいものなのだが、実際研究をしたり、理論を展開するとなるとそうともいかない。
むしろ、複雑である。
その複雑な関数の連続性を議論するときに「$\delta$をどうやって取ればいいかな…」ということもまた複雑である。
しかし、関数の各部分が連続であることがわかれば、全体も連続である、という主張なのだから連続性を確かめる回数は増えるかもしれないが、個々の連続性の議論をシンプルにすることができる。

つまり、複雑な関数の連続性を考えやすい関数に落とし込むことができるのは、

• 連続関数の和・差・積・商も連続である。
• 多項式関数は連続である。
• 有理関数は連続である。
• 連続な関数の合成関数も連続である。

が成り立っているが故なのである。

例を挙げよう。

例8. $f:\mathbb{R}_{>0}\to\mathbb{R}_{>0}$および$g:\mathbb{R}_{>0}\to\mathbb{R}_{>0}$が$f(x)=2x$、$g(x)=\sqrt{x}$で定められているとする。
このとき、$g\circ f$は$\mathbb{R}_{>0}$で連続である。

(証明)
$f:\mathbb{R}_{>0}\to\mathbb{R}_{>0}$は全単射であるので、$y\in \mathbb{R}_{>0}$に対して、$y=f(x)$なる$x\in\mathbb{R}$が存在する(全射だから)。
従って、$f$と$g$の合成関数を考えることができる。
このとき、
$$(g\circ f)(x)=g(f(x))=g(2x)=\sqrt{2x}$$
である。
今回示したいのは、
$$(\forall a\in\mathbb{R}_{>0})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}:0<|x-a|<\delta\Rightarrow |\sqrt{2x}-\sqrt{2a}|<\epsilon)$$
である。
つまり、上記を満たす$\delta$を見つけてくれば良い。

$\delta=\dfrac{\epsilon^2}{2}+\dfrac{2\sqrt{a}}{\sqrt{2}}\epsilon$とすると、$\delta>0$であり、$|x|<|a|+\delta$であるから、
$$\begin{eqnarray} |\sqrt{2x}^-\sqrt{2a}|&=&\sqrt{2}|\sqrt{x}-\sqrt{a}|\\ &<&\sqrt{2}(\sqrt{|a|+\delta}-\sqrt{a})\\ &=&\sqrt{2}\left( \sqrt{|a|+\frac{\epsilon^2}{2}+\frac{2\sqrt{a}}{\sqrt{2}}\epsilon}-\sqrt{2} \right)\\ &=&\sqrt{2}\left( \sqrt{\left( \sqrt{a} \right)^2+\left( \frac{\epsilon}{\sqrt{2}} \right)^2+2\cdot\frac{\epsilon}{\sqrt{2}}\cdot\sqrt{a}} -\sqrt{a}\right)\\ &=&\sqrt{2}\left( \sqrt{\left( \frac{\epsilon}{\sqrt{2}}+\sqrt{a} \right)^2} -\sqrt{a} \right)\\ &=&\sqrt{2}\left( \frac{\epsilon}{\sqrt{2}}+\sqrt{a} -\sqrt{a} \right)\\ &=&\epsilon \end{eqnarray}$$
従って、
$$(\forall a\in\mathbb{R}_{>0})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in \mathbb{R}:0<|x-a|<\delta\Rightarrow |\sqrt{2x}-\sqrt{2a}|<\epsilon)$$
が成り立ったので、$g\circ f$は$\mathbb{R}_{>0}$で連続である。
(Q.E.D.)

では、連続な関数の合成関数もまた連続な関数であるという主張を明示しよう。

「条件$f(I)\subset J$っている？」と思うかもしれないが、この条件がないと、合成関数を考えることができない。

「おや？これは極限であって関数が連続であることとは関係なくね？」と思うかもしれないのだが、$c=(g\circ f)(a)$の場合を考えれば、上記の主張はそのまま、連続な関数の合成関数は連続な関数である、という主張になる。

(証明)
示したいことは、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow |(g\circ f)(x)-c|<\epsilon)$$
である。
$\displaystyle \lim_{y\to b}g(y)=c$であるから、
$$(\forall \epsilon_1>0)(\exists \delta_1>0)\ {\rm s.t.}\ (\forall y\in J:0<|y-b|<\delta_1\Rightarrow |g(y)-c|<\epsilon)$$
が成り立っている。
さらに、
$\displaystyle \lim_{x\to a}f(x)=b$であるから、
$$(\forall \epsilon_2>0)(\exists \delta_2>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta_2\Rightarrow |f(x)-b|<\epsilon_2)$$
が成り立っている。
ここで、$\epsilon_2>0$は任意の正の実数であるから、$\epsilon_2=\delta_1$でも成り立つ。
従って、
$$(\forall a\in I)\ 0<|x-a|<\delta_2\rightarrow |f(x)-b|<\delta_1$$
が成り立つ。
従って、$\delta$として、$\delta_2$を採用する。
上記を満たすような$x\in I$に対して、$y=f(x)$と書くことで、
$|f(x)-b|<\delta_1$により$|y-b|<\delta_1$が成り立つ。
従ってこのような$y$で$|g(y)-c|<\epsilon_1$であるから、
$$|g(y)-c|=|g(f(x))-c|<\epsilon_1$$
を満たす。
ここで、$\epsilon_1$は任意の正の実数なので、新たに$\epsilon$と書き直すと、
$$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x-a|<\delta\Rightarrow |(g\circ f)(x)-c|<\epsilon)$$
が成り立った。
従って、合成関数の極限が成り立つ。
(Q.E.D.)

関数の発散

ある点付近での発散

数列と同様に、関数にも発散する関数がある。
「数列のときと同じだぜ！」と言いたいところだが、若干違う。
関数の収束の話でもそうだが、全く同じというわけではない。
しかし、似てる。
一言で言えば、

である。
「ある点の付近」というのは、「ある点$a$との距離が$\delta$未満であるような$x$に対しては」という意味である。
(関数の収束と同じだネ)

以上のことを論理式で書くと次である。

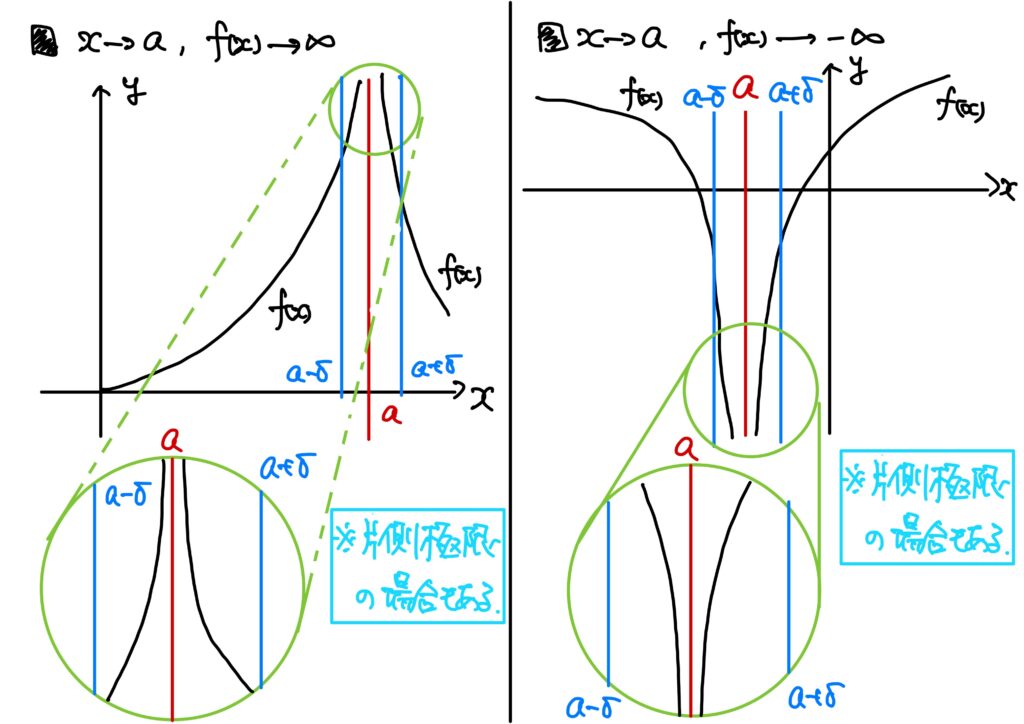
例9
$f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$が$f(x)=\dfrac{1}{x^2}$で定められているとする。
このとき、$\displaystyle\lim_{x\to 0}\frac{1}{x^2}=\infty$である。

(証明)
示したいことは
$$(\forall U\in\mathbb{U})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow \frac{1}{x^2}>U)$$
である。
つまり、上記を満たすような$\delta>0$を見つけこれれば良い。
任意の$U\in\mathbb{R}$に対して、$\delta=\dfrac{1}{\sqrt{U}}$とすると、$\delta>0$である。
$0<|x|<\delta$を満たすような任意の$x\in\mathbb{R}\setminus\{0\}$に対して、

$$\begin{eqnarray} \frac{1}{x^2}&=&\frac{1}{|x|^2}>\frac{1}{\delta^2}=\frac{1}{\left(\frac{1}{\sqrt{U}} \right)^2}=U \end{eqnarray}$$

従って、 $$(\forall U\in\mathbb{U})(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:0<|x|<\delta\Rightarrow \frac{1}{x^2}>U)$$
が成り立ったので、$\displaystyle\lim_{x\to 0}\frac{1}{x^2}=\infty$である。
(Q.E.D.)

「最終的に関数の値はどうなるの？」について

最終的に値が収束する場合

これは、殆ど数列の極限と同じ考え方である。
数列の極限は、平たくいえば「ある番号以降の数列の値がある実数と十分近いときに収束するという。」のであった。
関数に対しては、番号ではなく

なのである。
つまり、そんな$U$が見つかれば、「$f$は$A$に収束するという」わけである。

これを論理式で書けば、次である。

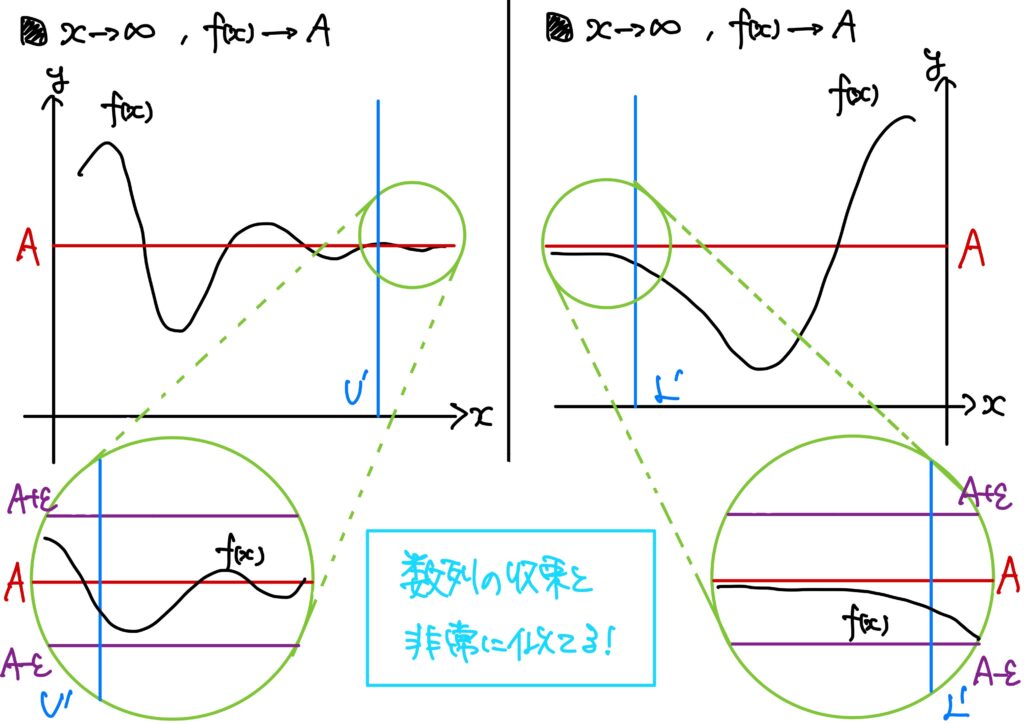
例9
$f:\mathbb{R}\setminus\{0\}\to\mathbb{R}$が$f(x)=\dfrac{1}{x^2}$で定められているとする。
このとき、$\displaystyle\lim_{x\to \infty}\frac{1}{x^2}=0$である。

(証明)
示したいことは
$$(\forall \epsilon>0)(\exists U’>0)\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow\left|\frac{1}{x^2}\right|<\epsilon\right)$$
である。
任意の$\epsilon>0$に対して、$U’=\dfrac{1}{\sqrt{\epsilon}}$とする。
$x>U’$なる$x\in\mathbb{R}\setminus\{0\}$に対して、

$$\left|\frac{1}{x^2}\right|=\frac{1}{x^2}<\frac{1}{U’^2}=\frac{1}{\frac{1}{\sqrt{\epsilon}^2}}=\epsilon$$

であるから、
$$(\forall \epsilon>0)(\exists U’>0)\ {\rm s.t.}\ \left(\forall x\in I:x>U’\Rightarrow\left|\frac{1}{x^2}\right|<\epsilon\right)$$
が成り立ったので、$\displaystyle\lim_{x\to \infty}\frac{1}{x^2}=0$である。
(Q.E.D.)

最終的に収束せず発散する場合

今までの話を組み合わせれば、直ちに分かる。
というのも、

のである。
つまり、ある程度大きい$x$に対しては、$f(x)$がどんな実数よりも大きいときに、関数$f$は$x\to\infty$で$\infty$に発散するという、わけなのである。

これを論理式で書けば、次である。

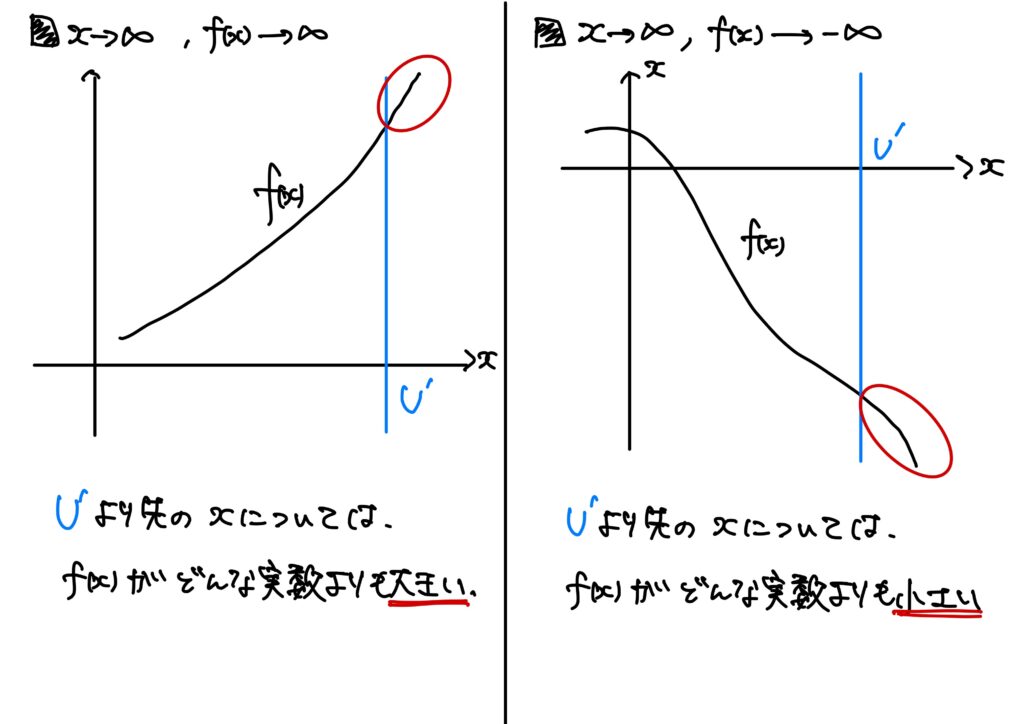
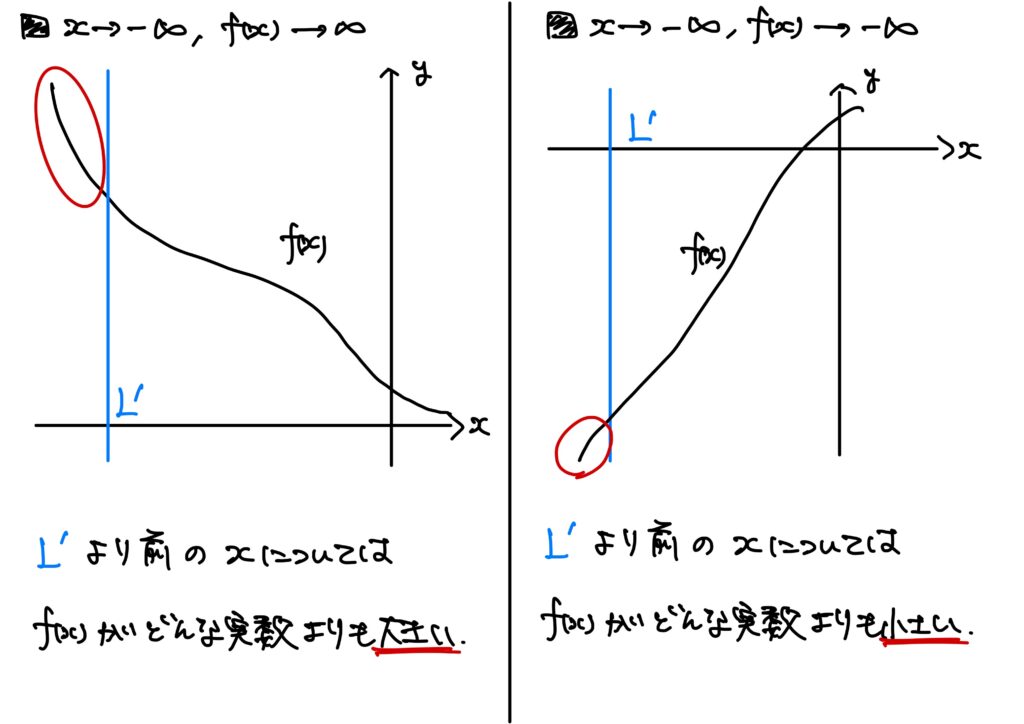
少々まとめてみると、

• $x\to\infty$で$f(x)\to\infty$
• $x\to\infty$で$f(x)\to-\infty$
• $x\to-\infty$で$f(x)\to\infty$
• $x\to-\infty$で$f(x)\to-\infty$

の4パターンがある、と言っているわけである。

例10. $g:\mathbb{R}\to\mathbb{R}$が$g(x)=x^2$で定められているとする。
このとき、$\displaystyle\lim_{x\to \infty}x^2=\infty$である。

(証明)
示したいことは
$$(\forall U\in\mathbb{R})(\exists U’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in\mathbb{R}:x>U’\Rightarrow x^2>U)$$
である。
任意の$U\in\mathbb{R}$に対して、$U’=\sqrt{\epsilon}$とする。
$x>U’$なる$x\in\mathbb{R}$に対して、

$$x^2>U’^2=\left(\sqrt{U}\right)^2=U$$

であるから、
$$(\forall U\in\mathbb{R})(\exists U’\in\mathbb{R})\ {\rm s.t.}\ (\forall x\in\mathbb{R}:x>U’\Rightarrow x^2>U)$$
が成り立ったので、$\displaystyle\lim_{x\to \infty}x^2=\infty$である。
(Q.E.D.)

結

今回は「多項式関数と有理関数は連続」「連続関数の合成関数も連続関数」「関数の発散」について解説した。

「多項式関数と有理関数は連続」と「連続関数の合成関数も連続関数」という事実から、一言で言えば、

ということである。
またこの事実によって、複雑な関数であっても、部分部分で連続であれば、全体の連続性も議論しやすくなるわけである。

また、数列と同様に関数にも発散という概念がある。
数列の場合と違うのは

• $x\to a$で$f(x)\to\infty$
• $x\to a$で$f(x)\to-\infty$
• $x\to\infty$で$f(x)\to\infty$
• $x\to\infty$で$f(x)\to-\infty$
• $x\to-\infty$で$f(x)\to\infty$
• $x\to-\infty$で$f(x)\to-\infty$

の6パターンあるということだ。
しかしながら、結局は数列の発散と殆ど同じで、

• ある点付近で、関数の値がどんな実数よりも大きい。
• ある点付近で、関数の値がどんな実数よりも小さい。
• ある程度大きい実数に対する関数の値がどんな実数よりも大きい。
• ある程度大きい実数に対する関数の値がどんな実数よりも小さい。
• ある程度小さい実数に対する関数の値がどんな実数よりも大きい。
• ある程度小さい実数に対する関数の値がどんな実数よりも小さい。

というわけである。

次回は多変数関数の極限と連続性について説明する。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！