本記事の内容
本記事は区間縮小法とアルキメデスの原理からボルツァーノ-ワイエルシュトラスの定理を証明し、実数の連続性との関係を説明する記事です。
本記事を読むにあたり「区間縮小法」と「アルキメデスの原理」を知っている必要があるため、以下の記事も合わせて御覧ください。
ボルツァーノ-ワイエルシュトラスの定理の明示とその証明
ボルツァーノ-ワイエルシュトラスの定理を一言で述べれば、
ということでした。
では明示しましょう。
数列\(\{x_n\}_{n\in\mathbb{N}}\)が有界な数列ならば、その数列に対する収束する部分列が存在する。
先述の通り、この定理の証明には区間縮小法とアルキメデスの原理を使います。
これらは使うときに改めて明示します。
証明の前に証明の流れを説明します。
- (ステップ1) 数列\(\{x_n\}_{n\in\mathbb{N}}\)が有界である、という条件を言い換える。
- (ステップ2) 縮小する区間とそれから得られる数列を作る。
- (ステップ3) \(\{x_n\}_{n\in\mathbb{N}}\)の部分列を作る。
- (ステップ4) さっき作った部分列が収束することを示す。
「はさみうちの原理」を使う。道中で証明する。
ボルツァーノ-ワイエルシュトラスの定理の証明
(ステップ1)
数列\(\{x_n\}_{n\in\mathbb{N}}\)が有界であるとします。
すなわち、数列\(\{x_n\}_{n\in\mathbb{N}}\)が上に有界であり、かつ下に有界であるとします。
このとき、次が成り立つ。
- ある実数\(R_1\)が存在して、\(\forall n\in\mathbb{N}\)に対して、\(x_n\leq R_1\)を満たす。
- ある実数\(R_2\)が存在して、\(\forall n\in\mathbb{N}\)に対して、\(R_2\leq x_n\)を満たす。
この2つの条件をまとめて書くことができます。
というのも、実数\(R\)を\(|R_1|\)と\(|R_2|\)のうち大きい方とします。
記号で書けば、\(R=\max\{|R_1|,|R_2|\}\)とします。
すると、\(R\geq |R_1|\)かつ\(R\geq|R_2|\)なのだから、\(-R\leq R_1\leq R\)かつ\(-R\leq R_2\leq R\)です
従って、\(-R\leq R_2\leq x_n\leq R_1\leq R\)です。
ゆえに上記の2条件は1行で次のように書けるわけです。
$$(\exists R\in\mathbb{R})\ {\rm s.t.}\ (\forall n\in\mathbb{N})\ -R\leq x_n\leq R$$
(ステップ2)
次にこの条件で縮小する区間を作ります。
実は、これは以前証明した「区間縮小法+アルキメデスの原理\(\Rightarrow\)デデキントの定理」の証明(【解析学の基礎シリーズ】実数の連続性編 その12)と殆ど同じです。
この証明では切断を考えるわけではないので、そこが違うだけで、作り方は殆ど一緒です。
ここで、実数\(-R\)を\(a_1\)、実数\(R\)を\(b_1\)と書いたとする(\(a_1=-R,\ b_1=R\)とする)と、任意の\(n\in\mathbb{N}\)に対して\(a_1\leq x_n\leq b_1\)であるので、任意の\(n\in\mathbb{N}\)に対して\(x_n\in[a_1,b_1]\)となる区間\([a_1,b_1]\)を作ることができます。
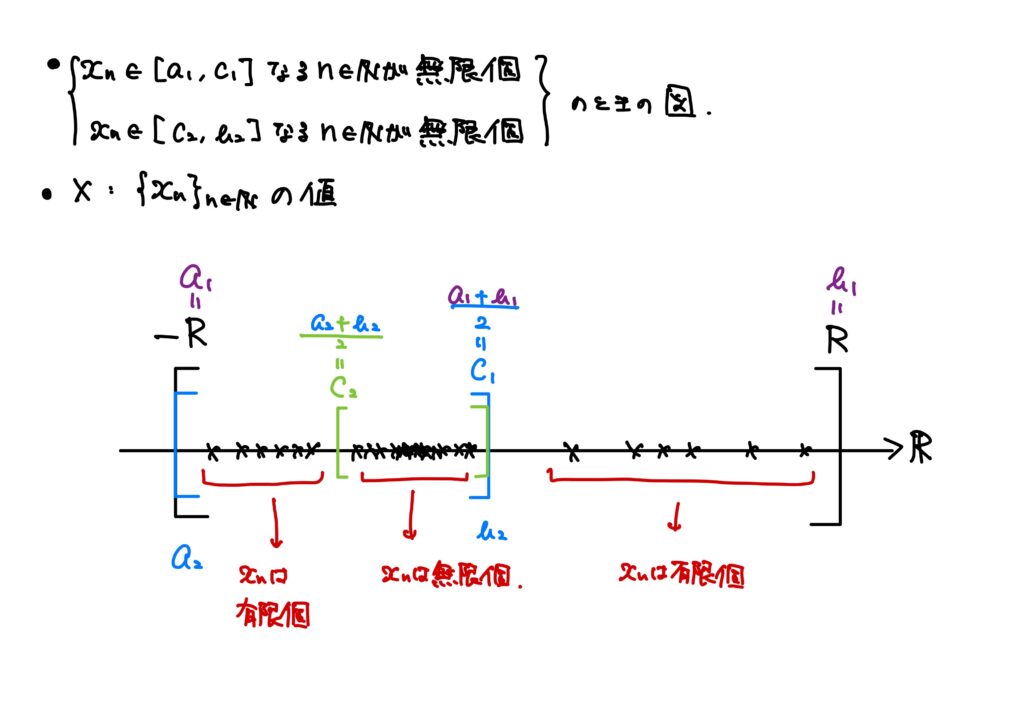
このとき、\([a_1,b_1]\)の中間の点(\(a_1\)と\(b_1\)の真ん中の点)を\(c_1\)とします。
すなわち、\(\displaystyle c_1=\frac{a_1+b_1}{2}\)とします。
このとき、次のいずれか一方、もしくは片方が必ず成り立ちます(両方とも成り立たないということはありません)。
- \(x_n\in[a_1,c_1]\)を満たすような番号\(n\in\mathbb{N}\)が無限個存在する。
- \(x_n\in[c_1,b_1]\)を満たすような番号\(n\in\mathbb{N}\)が無限個存在する。
仮に、両方成り立たないとすると、すなわち、\([a_1,c_1]\)に含まれる\(x_n\)と\([c_1,b_1]\)に含まれる\(x_n\)がどちらも有限個しか無かったとすると、\([a_1,b_1]\)の中に\(x_n\)が有限個しか存在しないことになってしまい、矛盾です。
- 1.が成り立つとき
\(a_2=a_1\)、\(b_2=c_1\)とおきます。 - 2.が成り立つとき
\(a_2=c_1\)、\(b_2=b_1\)とおきます。
すると、\(x_n\in[a_2,b_2]\)となる番号\(n\in\mathbb{N}\)は無限個存在します。
同様にして、\(a_n\)および\(b_n\)を定めれば、数列\(\{a_n\}_{n\in\mathbb{N}}\)は単調増加数列、数列\(\{b_n\}_{n\in\mathbb{N}}\)は単調減少数列です。
次で示します。
今、任意の\(n\in\mathbb{N}\)に対して
- \(a_n=a_{n-1},\ b_n=c_{n-1}=\displaystyle \frac{a_{n-1}+b_{n-1}}{2}\)
- \(a_n=c_{n-1}=\displaystyle \frac{a_{n-1}+b_{n-1}}{2},\ b_n=b_{n-1}\)
のいずれか一方が成り立ちます。
前者の場合を考えます。
\(a_n=a_{n-1}\)であるので\(a_n\geq a_{n-1}\)だから\(a_n\geq a_{n-1}\)です。
また、\(b_n=\displaystyle\frac{a_{n-1}+b_{n-1}}{2}\)であるから、\(\displaystyle b_n-b_{n-1}=\frac{a_{n-1}+b_{n-1}}{2}-b_{n-1}=\frac{a_{n-1}-b_{n-1}}{2}\leq0\)であるため(任意の\(n\in\mathbb{N}\)で\(a_n\leq b_n\)により。)、\(b_n\leq b_{n-1}\)です。
同様に後者の場合を考えます。
\(a_n=\displaystyle\frac{a_{n-1}+b_{n-1}}{2}\)であるから、\(\displaystyle a_n-a_{n-1}=\frac{a_{n-1}+b_{n-1}}{2}-a_{n-1}=\frac{b_{n-1}-a_{n-1}}{2}\geq0\)であるため(任意の\(n\in\mathbb{N}\)で\(a_n\leq b_n\)により)、\(a_n\geq a_{n-1}\)です。
また、\(b_n=b_{n-1}\)であるので\(b_n\geq b_{n-1}\)だから\(b_n\leq b_{n-1}\)です。
従って、\(\{a_n\}_{n\in\mathbb{N}}\)は単調増加数列、\(\{b_n\}{n\in\mathbb{N}}\)は単調減少数列です。
このとき、区間\([a_n,b_n]\)の長さは\(\displaystyle b_n-a_n=\frac{2R}{2^{n-1}}\)す。
また、\(\displaystyle\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}\frac{2R}{2^{n-1}}=0\)です。
これを示すためにアルキメデスの原理を使います。
しかし、これはすでに証明を与えています(【解析学の基礎シリーズ】実数の連続性編 その12)。
従って、今、任意の\(n\in\mathbb{N}\)に対して、\(a_n<b_n\)であり、かつ\(\displaystyle\lim_{n\to\infty}(b_n-a_n)=0\)が成り立っているので、区間縮小法の仮定を満たします。
区間縮小法は何だったかというと、
- 任意の\(I_n\)に含まれる実数が存在する。すなわち $$\bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$$,
- 特に、\(I_n=[a_n,b_n]\)として、\(\displaystyle \lim_{n\to\infty}(b_n-a_n)=0\)であれば(すなわち、区間がどんどん小さくなっていけば)、共通部分は一点\(\alpha\)のみからなる集合である。すなわち、 $$\bigcap_{n\in\mathbb{N}}I_n=\{\alpha\}$$ である。このとき、 $$\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=\alpha$$ である。
でした。
区間縮小法から、
$$(\exists c\in\mathbb{R})\ {\rm s.t.}\ c=\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n$$
が成り立ちます。
(ステップ3)
次に、\(\{x_n\}_{n\in\mathbb{N}}\)の部分列を次のように与えます。
- \(n_1=1\)とする。(\(x_1\in[-R,R]=[a_1,b_1]\))
- \(x_{n_1},\dots,x_{n_{k-1}}\)まで定まったとして、
$$x_n\in[a_k,b_k],\ n>n_{k-1}$$
を満たす\(n\in\mathbb{N}\)(これは無限個存在します。というより、無限個になるようにどんどん区間を狭めていく方法で区間を作りました。)のうち、最小の自然数を\(n_k\)とおきます。
例えば、\(n_2\)はどのように決まるかというと、\(x_n\in[a_2,b_2]\)かつ\(n>n_1\)を満たすような自然数\(n\)の中で最小の自然数を\(n_2\)とおくので、\(n_1=1\)だから\(n>1\)なる自然数\(n\)で、\(x_n\in[a_2,b_2]\)を満たす最小の自然数が\(n_2\)です。。
ここで、必ずしも\(x_2\in[a_2,b_2]\)とは限らないので、\(n_2=2\)とは限りません。
さらに、新たに作った数列\(\{n_k\mid k\in\mathbb{N}\}\)は狭義単調増加数列です。
実際、\(n_k\)は\(x_n\in[a_k,b_k]\)かつ\(n>n_{k-1}\)を満たす自然数\(n\)の中で最小のものなので、\(x_{n_k}\in[a_k,b_k]\)かつ\(n_k>n_{k-1}\)を満たすから、狭義単調増加数列です。
従って、任意の\(k\in\mathbb{N}\)に対して、\(x_{n_k}\in[a_k,b_k]\)なのだから、任意の\(k\in\mathbb{K}\)に対して\(a_k\leq x_{n_k}\leq b_k\)です。
この\(\{x_{n_k}\}_{k\in\mathbb{N}}\)が収束していれば証明は終わります。
(ステップ4)
ここで、次の事実を使います。
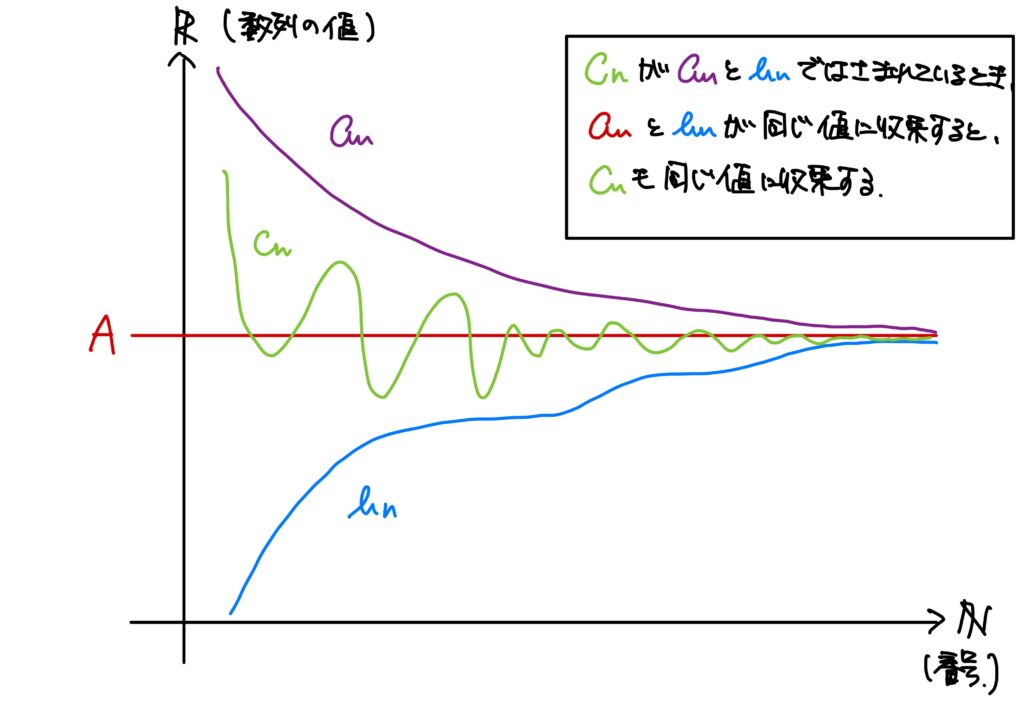
\(\{a_n\}_{n\in\mathbb{N}}\)、\(\{b_n\}_{n\in\mathbb{N}}\)、\(\{c_n\}_{n\in\mathbb{N}}\)を実数の数列とする。 このとき、任意の\(n\in\mathbb{N}\)に対して\(a_n\leq c_n\leq b_n\)が成り立ち、かつある実数\(A\)に対して\(\displaystyle \lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=A\)が成り立つならば、\(\displaystyle\lim_{n\to\infty}c_n=A\)である。
はさみうちの原理の証明
示すべきは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |c_n-A|<\epsilon)$$
です。
つまり、上記を満たすような\(N\in\mathbb{N}\)を見つけてくれば良いです。
今、\(\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=A\)が成り立っています、すなわち、数列\(\{a_n\}_{n\in\mathbb{N}}\)および\(\{b_n\}_{n\in\mathbb{N}}\)が共に\(A\)に収束しているのだから、
- \((\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\epsilon_1)\)
- \((\forall \epsilon_2>0)(\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-A|<\epsilon_2)\)
が成り立っています。
つまり、上記をそれぞれ満たすような自然数\(N_1\)および\(N_2\)を見つけることができます。
さらに、上記は全ての正の実数\(\epsilon_1\)および\(\epsilon_2\)で成り立つのだから、\(\epsilon=\epsilon_1=\epsilon_2\)としても成り立ちます。
ここで、\(N\)を\(N_1\)と\(N_2\)のうち、大きい方とします。
記号で書けば、\(N=\max\{N_1,N_2\}\)とします。
すると、\(n\geq N\)を満たす自然数\(n\)に対して、
$$|a_n-A|<\epsilonかつ|b_n-A|<\epsilon$$
が任意の正の実数\(\epsilon\)に対して成り立っています。
仮定から、任意の\(n\in\mathbb{N}\)に対して\(a_n\leq c_n\leq b_n\)であるから、\(a_n-A\leq c_n-A\leq b_n-A\)です。
さらに、\(|a_n-A|<\epsilon\)かつ\(|b_n-A|<\epsilon\)なのだから、
$$-\epsilon<a_n-A\leq c_n-A\leq b_n-A<\epsilon$$
です。
故に\(-\epsilon<c_n-A<\epsilon\)であるから、
$$\forall n\in\mathbb{N})\ n\geq N\Rightarrow |c_n-A|<\epsilon$$
を満たします。
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |c_n-A|<\epsilon)$$
であるから、\(\displaystyle \lim_{n\to\infty}c_n=A\)です。
はさみうちの原理の証明終わり
(ステップ4)の証明に戻る。
今、\(\displaystyle \lim_{k\to\infty}a_k=\lim_{k\to\infty}b_k=c\)なのだから、はさみうちの原理により、
$$\lim_{k\to\infty}x_{n_k}=c$$
となり、\(\{x_{n_k}\}_{k\in\mathbb{N}}\)は収束します。
ボルツァーノ-ワイエルシュトラスの定理の証明終わり
余談その2(読み飛ばしてOKだけど結構重要だと思うのでもしよかったら読んでください。)
「証明は読んで、なんとなく分かるし、正しいな。」と思うけれども、なにか腑に落ちないというか、「これ、本当に分かったのかな。」と不安にならなかったでしょうか。
筆者は一番最初「ふーん。そうやって証明するんだ。」と単に思っただけだったのだが、再びこの定理の証明に取り掛かったとき、「ん〜。まあ確かに正しいけれども。なんか腑に落ちないというか、分かった気になってるだけじゃね?」と少々不安になりました。
もし読者がその感覚を持っているのであればぜひ大事にしてほしい。
というのも、腑に落ちないというかモヤモヤしていることの根底には「なんでそんなの思いつくんだよ。」という、どうしてその発想に至ったのかがわからいという疑問があるからだと筆者は思います。
この「どうしてその発想に至ったのか」ということが分かって真に理解したと言えるのではないかと感じています。
今回の場合においては、「数列が収束するとは?」という条件を別の視点から言い換えてみると光が見えてくると思われます。
数列\(\{a_n\}_{n\in\mathbb{N}}\)が\(a\in\mathbb{R}\)に収束するというのは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-a|<\epsilon)$$
が成り立つということでした。
これは今まで、
というような説明してきました。
しかし、言い方を変えてみると、
とも言えるのです。
「ある番号\(N\)以降は全部\(|a_n-a|<\epsilon\)が成り立つ」のだから、その番号までは、すなわち\(N-1\)番目までは\(|a_n-a|\geq\epsilon\)が成り立つということです。
つまり、\(|a_n-a|\geq\epsilon\)が成り立つような\(a_n\)は\(N-1\)個しか無いのだから有限個しか存在しないのです。
より直感的に言えば、収束する数列というのは、収束先に(極限に)近づけば近づくほど点が密集している、ということなのです。
今、収束するような部分列を見つけたいのだから、結局は収束する数列を作りたいわけです。
それ故、「より点が密集しているのはどこかな?」ということを区間の長さを半分ずつにしていくことで探索し、収束する数列を見つけようとした、ということがこの部分列を作るときの初手の発想です(と思います)。
部分列は単に数列の一部分を取ってくればよいのではなくて、順番が大事です。
もし、単に数列の一部分を取ってきてしまったら、収束しなくなってしまう場合があります。
これは先に述べた「収束先に(極限に)近づけば近づくほど点が密集しているのが収束列である」ということに反してしまう可能性があるからです。
ゆえに順番が大事なのだが、その順番を正しく並べるために\(x_n\in[a_k,b_k]\)かつ\(n>n_{k-1}\)が成り立つような自然数\(n\)の中で最小のものを選んで新しい番号としています。
これにより正しい順番が担保されているのです。
実数の連続性との関係は?
実数の連続性との関連は序で少々述べたとおりです。
つまり、ボルツァーノ-ワイエルシュトラスの定理は
という直感に対応します。
というのも、結局は収束する数列が見つけてこれる、という話なのだから、直感としては上記に対応するのです。
ちょいと補足しておけば、「有界な閉区間の中のどんな数列に対しても、その一部をうまく取ることで収束列を作り上げることができる。」ということがこの定理の主張です。
つまり、「有界な閉区間さえあれば、適当に数列を作ったとしても、その数列が収束するか否かに関わらず、その閉区間の中で必ず収束する数列を新たに作れる」ということです。
そういう意味でこれは強力な定理だと言えるのではないかと感じます。
話を戻すと、実はボルツァーノ-ワイエルシュトラスの定理から「ある数列が収束することと、その数列がコーシー列であるということは同値」(これを単に「コーシー列の収束」ということもある)ということが証明されます。
さらに、この命題からワイエルシュトラスの上限公理を導き出す事ができるので、
- デデキントの定理
- ワイエルシュトラスの上限公理
- 有界な単調列は収束する。
- 区間縮小法+アルキメデスの原理
- ボルツァーノ-ワイエルシュトラスの定理
- コーシー列の収束
が同値であることが分ります。
これは後の記事(↓)で解説します。
結
今回は区間縮小法とアルキメデスの原理からボルツァーノ-ワイエルシュトラスの定理の証明をした。
実は、この定理の証明は区間縮小法の証明と作業が似ているということが特徴である。
また、余談として筆者の頭の中も少々説明した。
参考になれば嬉しい。
次回は「コーシー列って?」ということについて書く。
ネタバラシしておくと、実数の範囲ではコーシー列は必ず収束する。
逆に収束列は必ずコーシー列である。
この事実からワイエルシュトラスの上限公理を導く事ができる。
故に、
- デデキントの定理
- ワイエルシュトラスの上限公理
- 有界な単調列は収束する。
- 区間縮小法+アルキメデスの原理
- ボルツァーノ-ワイエルシュトラスの定理
- コーシー列の収束
が同値であることが示される。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする