本記事の内容
本記事は、「実数って?」という素朴な疑問に答え、かつその性質である「連続性」とその意義について解説する記事である。
特に、整数、有理数という数は知っているという前提の元、無理数という数を発見し、実数を構成しよう、という話である。
中でも、「デデキントの切断」について解説する。
この記事を理解するためには、集合および論理の初歩を理解していることが前提であるため、そこに不安があれば、次の記事を参照してください。
※シリーズ化しているため、その一部のリンクを張っています。
さらに、今回は、前回解説した「デデキントの定理」についても知っている必要があるので、それもはせて参照してください。
序
実数の連続性と同値な命題はおおよそ6つある、ということを前回の記事で説明した。
中でも前回は「デデキントの切断」を皮切りに「デデキントの定理」を説明し、証明した。
実数の連続性は、直感的に
- 実数の数直線上には一切”すき間”が無い。
- どんな実数にもその十分近くにまた実数がある。
と理解できるのであった。
デデキントの定理は「実数の数直線上には一切”すき間”が無い。」に対応する。
今回は、「ワイエルシュトラスの上限公理(上限公理、有界性公理などとも呼ばれる)」をデデキントの定理から証明し、かつこれら2つの命題が同値であることを示す。
- \(A\)には最大値が無く、\(B\)には最小値\(r\)がある。
- \(A\)には最大値\(r\)があり、\(B\)には最小値がない。
ワイエルシュトラスの上限公理を一言で述べれば「天井があるような集合には上限と呼ばれるMAX値(最大値ではない。後述)が実数に存在しますよ」ということである。
これは「どんな実数にもその十分近くにまた実数がある。」に対応し、先のデデキント切断から証明することができる。
そのために、いくつか概念を導入する。
準備
上界、上限
例6.
区間\([0,1]=\{x\in \mathbb{R}\mid 0<x\leq 1\}\)は\(\mathbb{R}\)の部分集合であり、かつ\([0,1]\)の全ての元は\(1\)以下である。
例7.
区間\((2,3)=\{x\in \mathbb{R}\mid 2<x<3\}\)は\(\mathbb{R}\)の部分集合であり、かつ\((2,3)\)の全ての元は\(3\)より小さい。
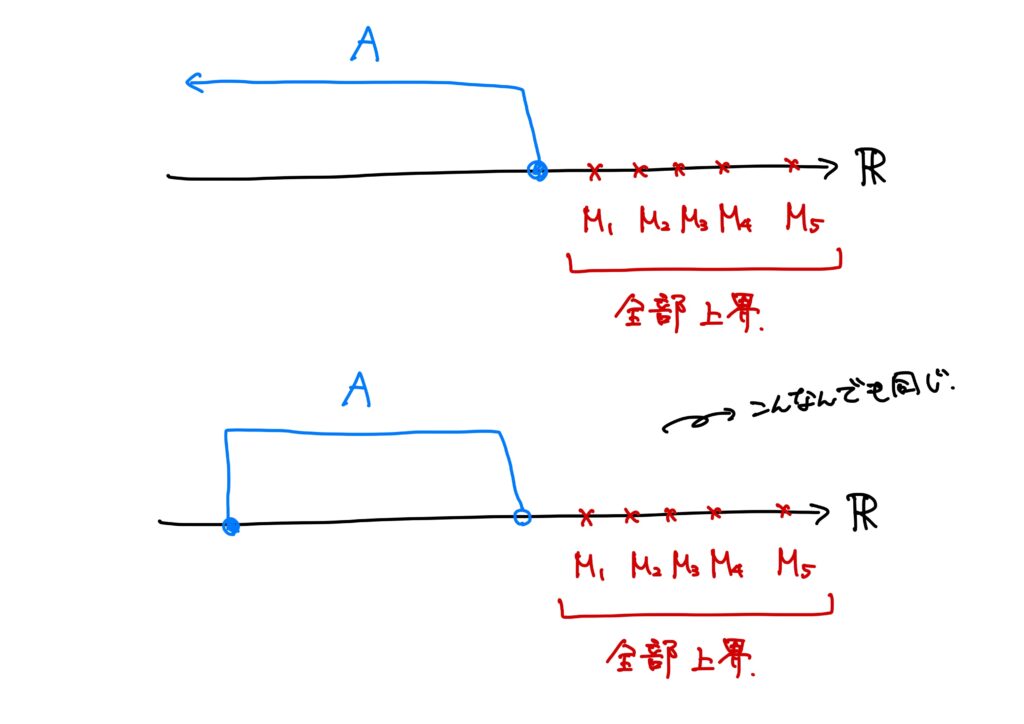
このように、\(\mathbb{R}\)の部分集合に対して、その部分集合のどんな元よりも大きいか等しい実数が存在するときに、その実数のことを上界(a upper bound)という。
要は、「ある実数の部分集合がとある実数を超えることはありませんよ」というその”とある実数”のことを上界と呼ぶというわけである。
これを論理式で書けば、
例6および例7について再度言及すると、例6については\(1\)以上であれば\(5\)も\(7\)も\(300\)も\([0,1]\)の上界であるし、上に有界。
例7については\(3\)以上であれば\(100\)も\(183\)も\(100000\)も\((2,3)\)の上界であるし、上に有界。
ポイントとしては、\(A\subset \mathbb{R}\)が空集合でなく、かつ上に有界であれば、上界は無限個存在する。
さらに、上界には必ず最小値が存在するということである。
ちなみに、例6では\(1\)が、例7では\(3\)が上界の最小値である。
この上界の最小値のことを上限(supremum)という。
言い方を変えると、「上界の中で、その上界よりも”ほんのちょっとでも”小さい実数はもう上界ではないという上界」のことを上限というのである。
「むしろわからん」となるかもしれないので、図を参照してほしい。
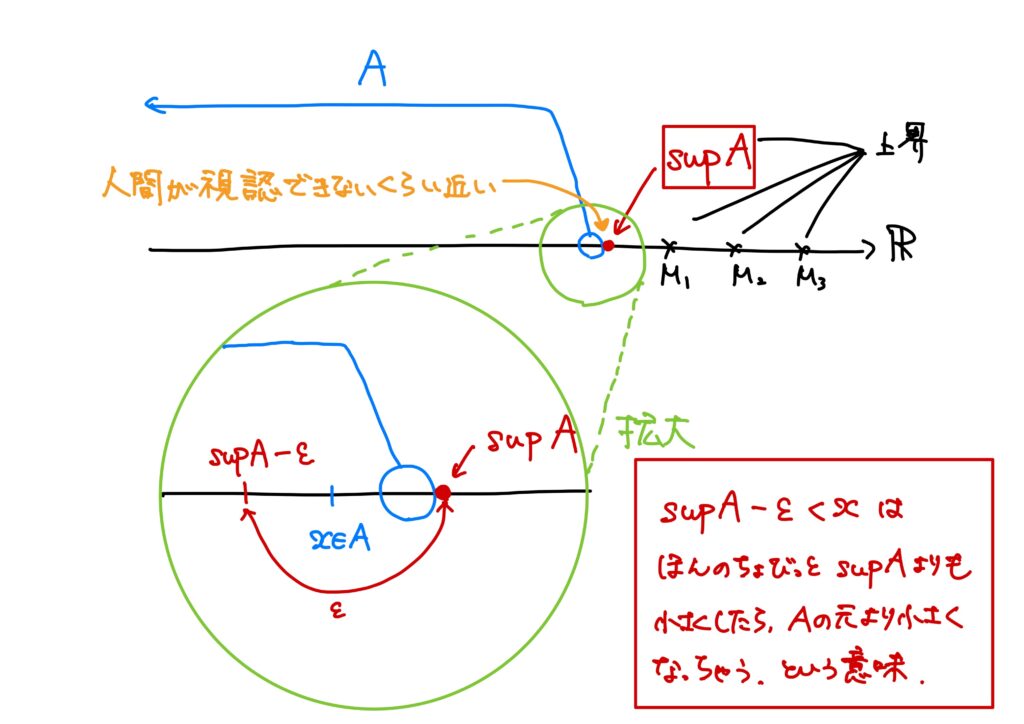
この上限を論理式で書くと、
- \(S\)は\(A\)の上界である。すなわち、次が成り立つ。$$\forall x\in A\ x\leq S$$
- \(S\)よりも小さい数は\(A\)の上界ではない。すなわち、次が成り立つ。 $$(\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>S-\epsilon$$
2.が「”ほんのちょっとでも”小さい実数はもう上界ではない」に対応する。
\(\epsilon\)は正であればどんな実数でも良いので、めちゃくちゃ小さくても良い(遠目に見たらほぼ0じゃね?という実数でも良いということ)。
よって、\(S-\epsilon\)は「\(S\)よりも”ほんのちょっとでも”小さい実数」に対応し、\(x>S-\epsilon\)は、「そんな実数は上界じゃないぜ」ということに対応する。
補足(下界と下限)※上界、上限とほぼ同じで上が下に変わるだけなので読み飛ばしてもOKです。
上界、上限に対応する概念として、「下界(”げかい”ではなく”かかい”)」、「下限」もある。
これは上界、上限の条件の不等式を逆にしたものであって、上界、上限が分かればなんてことはない。
例6.
区間\([0,1]=\{x\in \mathbb{R}\mid 0<x\leq 1\}\)は\(\mathbb{R}\)の部分集合であり、かつ\([0,1]\)の全ての元は\(0\)以上である。
例7.
区間\((2,3)=\{x\in \mathbb{R}\mid 2<x<3\}\)は\(\mathbb{R}\)の部分集合であり、かつ\((2,3)\)の全ての元は\(2\)より大きい。
このように、\(\mathbb{R}\)の部分集合に対して、その部分集合のどんな元よりも小さいか等しい実数が存在するときに、その実数のことを下界(かかい)(a lower bound)という。
要は、「ある実数の部分集合がとある実数よりも小さいなんてことはありませんよ」というその”とある実数”のことを下界と呼ぶというわけである。
これを論理式で書けば、

例6および例7について再度言及すると、例6については\(0\)以下であれば\(-5\)も\(-7\)も\(-300\)も\([0,1]\)の下界であるし、下に有界。
例7については\(2\)以下であれば\(-11\)も\(-183\)も\(-100000\)も\((2,3)\)の下界であるし、下に有界。
ポイントとしては、\(A\subset \mathbb{R}\)が空集合でなく、かつ下に有界であれば、下界は無限個存在する。
さらに、下界には必ず最大値が存在するということである(上界には最小値が存在するのだった)。
ちなみに、例6では\(0\)が、例7では\(2\)が下界の最大値である。
この下界の最大値のことを下限(infimum)という。
言い方を変えると、「下界の中で、その下界よりも”ほんのちょっとでも”大きい実数はもう下界ではないという下界」のことを上限というのである。
「むしろわからん」となるかもしれないので、図を参照してほしい。

下限を論理式で書くと、
- \(I\)は\(A\)の下界である。すなわち、次が成り立つ。$$\forall x\in A\ I\leq x$$
- \(I\)よりも大きい数は\(A\)の下界ではない。すなわち、次が成り立つ。 $$(\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ I+\epsilon>x$$
2.が「”ほんのちょっとでも”大きい実数はもう下界ではない」に対応する。
\(\epsilon\)は正であればどんな実数でも良いので、めちゃくちゃ小さくても良い(遠目に見たらほぼ0じゃね?という実数でも良いということ)。
よって、\(I+\epsilon\)は「\(I\)よりも”ほんのちょっとでも”大きい実数」に対応し、\(I+\epsilon>x\)は、「そんな実数は下界じゃないぜ」ということに対応する。
「最大値と上限って同じじゃね?」「いいえ、違います。」
最大値と上限(最小値と下限)は同じもののように思えるかもしれないが、実は違う。
例6.
区間\([0,1]=\{x\in \mathbb{R}\mid 0<x\leq 1\}\)は\(\mathbb{R}\)の最大値が\(1\)、最小値が\(0\)である。
また、上限は\(1\)であり下限は\(0\)である。
例7.
区間\((2,3)=\{x\in \mathbb{R}\mid 2<x<3\}\)は最大値も最小値も存在しない。
しかし、上限は\(100\)、下限は\(10\)である。
要は、最大値および最小値というのは、その集合の要素の中で最も大きい、最も小さい元のことを指すのである。
例7において、\(2\)および\(3\)というのは\((2,3)\)の元ではない。
折角なので、最大値および最小値とは何か。とうことを論理式で書いておく。
- \(\forall x\in A)(x\leq S)\),
- \(S\in A\).(これが上限との違い)
また、このとき、\(I\in\mathbb{R}\)が
- \(\forall x\in A)(x\geq I)\),
- \(I\in A\).(これが下限との違い)
要は、最大値(最小値)は”その集合の要素の中で”という条件がつくというわけである。
例6で見たように、最大値(最小値)と上限(下限)には一致することもある。
つまり、最大値(最小値)と上限(下限)はそれぞれ違うものだけれども似ているわけである。
それを表す事実を述べておく。
くどいようだが、この命題は決して「必ず最大値と上限は一致する」と言っているわけではない。
「最大値であれば、それは必ず上限である。」と言っているに過ぎないのである。
証明を与えてみよう。
ただし、最大値が上限であることの証明と最小値が下限であることの証明はほぼ同じなので、前者のみ証明を与えることにする。
(証明)
(1)最大値は上限であることの証明
\(A\subset\mathbb{R}\)に対して、\(S\)を\(A\)の最大値とする。
すなわち、
- \((\forall x\in A)(x\leq S)\),
- \(S\in A\).
を満たすとする。
このとき、\(S\)が\(A\)の上限であることを示したいので、
- \(\forall x\in A\ x\leq S\),
- \((\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>S-\epsilon\)
が成り立つことを証明すれば良い。
(1.について)仮定と同じものであるため、成り立つ。
(2.について)任意の\(\epsilon>0\)に対して、\(x>S-\epsilon\)となるような\(x\in A\)を見つけてくれば良い。
仮定から\(S\in A\)であるから、この\(x\)として\(S\)を取ることができる。
すると、この\(S\)は任意の\(\epsilon>0\)に対して、\(S>S-\epsilon\)を満たす(正の数を引けば、元の数よりも小さくなる)。
従って、2.も成り立つ。
(2)逆は成り立たない(上限だからといって必ずしも最大値ではない)の証明
上限は存在するのだが、最大値が存在しない例を挙げれば証明したことになる。
\(A=(2,3)=\{x\in\mathbb{R}\mid 2<x<3\}\)とすると、\(A\subset\mathbb{R}\)である。
このとき、
- \(\forall x\in A\ x\leq S\),
- \((\forall \epsilon>0)(\exists x\in A)\ {\rm s.t.}\ x>S-\epsilon\)
を満たすような\(S\)は存在するのだが、
① \((\forall x\in A)(x\leq S’)\),
② \(S’\in A\).
を満たすような\(S’\)は存在しないということを示すことができれば、証明完了である。
\(S=3\)とすれば、任意の\(x\in A\)に対して、\(x<3\)であるので、\(x\leq3\)であるから1.が成り立つ。
また、任意の\(\epsilon>0\)に対して、\(\epsilon<1\)のときは\(x=\displaystyle\frac{3+(3-\epsilon)}{2}=3-\frac{\epsilon}{2}\)とすれば、\(\displaystyle\frac{5}{2}<3-\frac{\epsilon}{2}<3\)であるから\(x\in A\)である。
一方\(3-\epsilon<3-\displaystyle\frac{\epsilon}{2}=x\)であるから\(x>3-\epsilon\)である。
\(\epsilon\geq1\)のとき、\(3-\epsilon\leq2\)により、\(x=\displaystyle\frac{5}{2}\)とすれば、\(x\in A\)であり、\(3-\epsilon\leq2<\displaystyle\frac{5}{2}=x\)であるから\(x>3-\epsilon\)である。
したがって、1.および2.が成り立つ。
また、1.により①が成り立つような\(S’\)が存在する。
この\(S’\)が同時に②を満たしていたとする。(背理法!)
つまり、\(S’\in A\)だったとする。
すると、\(S'<3\)である。
しかし、有理数の稠密性から、ある有理数\(c\)が存在して、\(S'<c<3\)である。
この\(c\)は\(2<S'<c<3\)により\(c\in A\)である。
しかしこれは、①に反する(\(S’\)が\(A\)の中で最も大きい数だったにもかかわらず、それよりも大きな\(A\)の要素\(c\)が存在することになる)。
よって①と②を同時に満たす\(S’\)は存在しない。
したがって、上限は必ずしも最大値ではない。
(Q.E.D)
ワイエルシュトラスの上限公理
ワイエルシュトラスの上限公理を述べて、その証明を与える。
先述したが、これはデデキントの定理から証明できる。
若干ネタバラシなのだが、その逆、すなわちワイエルシュトラスの上限公理を認めれば、デデキントの定理を示すことができる。
ワイエルシュトラスの上限公理は「天井があるような集合には上限と呼ばれるMAX値(最大値ではない)が実数に存在しますよ」とうことだと先に述べた。
これを今まで解説したことを思い出すと、上限は「その数よりも”ほんのちょっとでも”小さい数は上界じゃないぜ」という「その数」のことだった。
これはつまり、「どんな実数にもその十分近くにまた実数がある」ということが保証されなければ上限なんていうものは存在し得ない、ということになる。
ワイエルシュトラスの上限公理を認める、ということはこの上限の存在を保証することで、どんな実数にもその十分近くにまた実数があることを認めている、ということなのである。
論理式で書けば、
である。
ちなみに、公理ということをざっくり述べておくと「議論を行うための大前提」のことである。
ワイエルシュトラスの上限公理はデデキントの切断からデデキントの定理を導出することで、デデキントの定理から証明が可能なので、そういう言う意味では公理ではない。
ただし、後に述べるようにこれら2つは同値なので、ワイエルシュトラスの上限公理を大前提として議論をすすめる立場もある。
したがって、公理と呼んでいるのである。
(証明)
\(A\subset\mathbb{R}\)は空集合でなく、かつ上に有界であるとする。
また、\(A\)の上界の集合を\(B\)とする。
このとき、\(C=B^c=\mathbb{R}\setminus B\)とおくと、\((C,B)\)は\(\mathbb{R}\)の切断となっている。
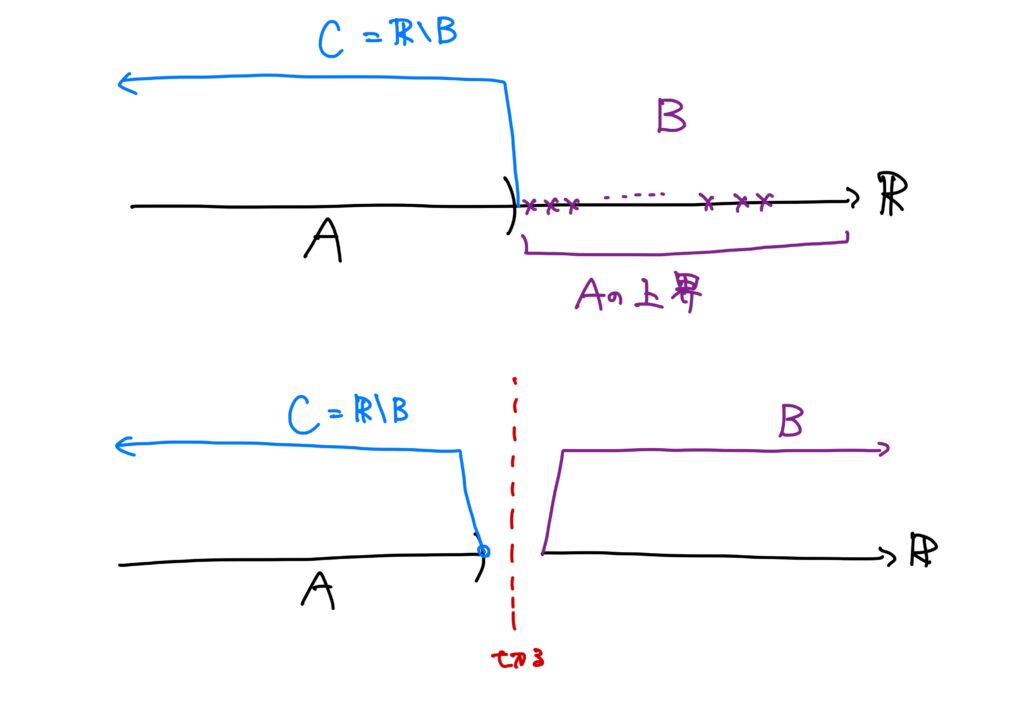
すなわち、次が成り立つ。
- \(\mathbb{R}=C\cup B\)
「\(\mathbb{R}\subset C\cup B\)かつ\(C\cup B\subset \mathbb{R}\)」を示す。(集合が等しいとはこれを示すことだった!もし不安があるようであれば、「【論理と集合シリーズ】その5を参照してください。)
任意の\(x\in\mathbb{R}\)に対して、\(x\)が\(A\)の上界であれば、\(x\in\mathbb{R}\)かつ\(x\in B\)である。
そうでなければ、\(x\in\mathbb{R}\)かつ\(x\not\in B\)である。
従って、\(x\in\mathbb{R}\setminus B\)または\(x\in B\)が成り立つので、\(x\in\mathbb{R}\setminus B\cup B=C\cup B\)である。(不安があれば【論理と集合シリーズ】その6を参照してください)
任意の\(x\in C\cup B\)に対して、\(x\in C\)であれ、\(x\in B\)であれ\(x\in \mathbb{R}\)である。
従って、\(\mathbb{R}=C\cup B\)である。 - \(C\cap B=\emptyset\)
仮に\(C\cap B\neq\emptyset\)とすると(背理法!)、ある\(z\)が存在して\(z\in C\cap B\)を満たす。
従って、「\(z\in\mathbb{R}\)かつ\(z\not\in B\)かつ\(z\in B\)」が真である事になってしまうが、これは偽であり矛盾。 - \(C\neq \emptyset\), \(B\neq \emptyset\)
\(B=\emptyset\)であれば(背理法!)、\(A\)に上界が存在しないことになるが、これは\(A\)が上に有界であることに矛盾。
ある\(x\in A\)に対して、\(x-1\not\in B\)である。
実際、\(x-1\in B\)であれば、任意の\(x\in A\)に対して\(x\leq x-1\)を満たすことになり、\(0\leq -1\)を得るため矛盾。
加えて、\(x\in A\subset \mathbb{R}\)であるから、\(x-1\in\mathbb{R}\)である。
従って、\(x-1\in\mathbb{R}\setminus B=C\)となり、\(C\neq\emptyset\)である。 - \(c\in C\)かつ\(b\in B\)ならば\(c<b\)
任意の\(c\in C\)は\(A\)の上界ではないので、\(c\not\in B\)であり、ある\(x_0\in A\)が存在して\(x_0>c\)(\(c\)が\(A\)の上界であることの否定!)を満たす。
また、\(b\in B\)により、任意の\(x\in A\)に対して\(x\leq b\)が成り立つ。
この命題は任意の\(x\in A\)について成り立つのだから、\(x_0\in A\)についても成り立つ。
つまり、\(x_0\leq b\)が成り立つ。
したがって、\(c<x_0\leq b\)であるから\(c<b\)である。
故に\((C,B)\)は\(\mathbb{R}\)の切断である。
デデキントの定理から、ある実数\(r\)が存在して、
- \(C\)には最大値が無く、\(B\)には最小値\(r\)がある。
- \(C\)には最大値\(r\)があり、\(B\)には最小値がない。
のいずれか一方が成り立つ。
2.が成り立ったとしよう。
つまり\(C\)には最大値\(r\)があり、\(B\)には最小値がないとする。
\(r\in C\)であれば、\((C,B)\)は切断であるから、\(r\not\in B\)である。
従って、\(r\)は\(A\)の上界ではない。
すなわち、\(x_0>r\)を満たすような\(x_0\in A\)が存在する。
これを論理式で書けば、
$$(\exists x_0\in A)\ {\rm s.t.}\ x_0>r(rがAの上界であることの否定!)$$
である。
ここで、\(\displaystyle\frac{s+x_0}{2}\)は\(r\)と\(x_0\)の間にある数(有理数とは限らない)であり、これを\(b\)とする。
すなわち、\(b=\displaystyle\frac{s+x_0}{2}\)とおけば、
$$r<b<x_0$$
を満たす。
これは\(b\)が\(A\)の上界でないことを表している。
故に\(b\in C\)である。
\(r\)は\(C\)の最大値であるから、任意の\(t\in C\)に対して、\(t\leq r\)を満たす。
\(b\in C\)であるから\(b\leq r\)も成り立つ。
従って、\(r<b\)と\(b\leq r\)が同時に成り立つので矛盾。
従って、2.の場合は起こり得ない。
すなわち、起こり得るのは1.の場合である。
つまり、\(C\)には最大値は存在せず、\(B\)には最小値\(r\)が存在する。
\(B\)とは\(A\)の上界の集合であり、上限とは上界の最小値であるから、\(r\)は\(A\)の上限である。(Q.E.D.)
デデキントの定理とワイエルシュトラスの上限公理は同値
本記事で最も大事なことである。
前節において、デデキントの定理を仮定しすることでワイエルシュトラスの上限公理を導いた。
実は、この逆、すなわちワイエルシュトラスの上限公理を仮定するとデデキントの定理が得られる。
- \(A\)には最大値が無く、\(B\)には最小値\(r\)がある。
- \(A\)には最大値\(r\)があり、\(B\)には最小値がない。
つまり、先のワイエルシュトラスの上限公理を仮定するとデデキントの定理を証明することができる。
(証明)
(1)デデキントの定理\(\Rightarrow\)ワイエルシュトラスの上限公理の証明
これは前節で証明済み。
(2)ワイエルシュトラスの上限公理\(\Rightarrow\)デデキントの定理
\(\mathbb{R}\)の任意の切断\((A,B)\)に対して、\(A\)は上に有界である。
実際、ある\(U\in\mathbb{R}\)が存在して、任意の\(a\in A\)に対して、\(a\leq U\)であればよい。
\((A,B)\)は切断であるので、任意の\(a\in A\)および任意の\(b\in B\)に対して\(a<b\)であるから、\(U\)として\(B\)の要素を取れば良い。
また、\((A,B)\)が切断であることから\(A\subset\mathbb{R}\)、\(A\neq\emptyset\)である。
従って、ワイエルシュトラスの上限公理から\(L\)には上限\(s=\sup A\)が存在する。
さらに、\((A,B)\)が切断であるので、\(\mathbb{R}=A\cup B\)かつ\(A\cap B=\emptyset\)であるから、\(s\in A\)か\(s\in B\)のいずれか一方が成り立つ。
\(s\in A\)のとき、\(s\)は\(A\)の最大値である。
実際、\(s\)は上限であり、上限は上界であるから、任意の\(x\in A\)対して、\(x\leq s\)が成り立つ。
仮定から\(s\in A\)であるので、\(s\)は\(A\)の最大値である。
一方\(s\in B\)であるとき、\(s\)は\(B\)の最小値である。
このとき、任意の\(b\in B\)に対して\(s\leq b\)であることを示せば良い。
任意の\(\epsilon>0\)について、\(s-\epsilon\)は、\(s\)が\(A\)の上限であることから、\(s-\epsilon\in A\)である。
ここで、\(s-\epsilon\)は\(s\)よりも小さい任意の実数を表すことに注意。
従って、\(s-\epsilon\in A\)は任意の\(x\in\mathbb{R}\)に対して、\(x<s\)ならば\(x\in A\)が成り立つことに他ならない。
この命題の対偶を取れば、「任意の\(x\in\mathbb{R}\)に対して\(x\not\in A\)ならば\(x\geq s\)」である。
\(\mathbb{R}=A\cup B\)かつ\(A\cap B=\emptyset\)であるから、\(x\not\in A\)は\(x\in B\)と同値である。
従って、任意の\(x\in\mathbb{R}\)に対して\(x\in B\)ならば\(x\geq s\)である。
以上により、
- \(A\)には最大値が無く、\(B\)には最小値\(\sup A\)がある。
- \(A\)には最大値\(\sup A\)があり、\(B\)には最小値がない。
のいずれか一方が成り立つことが示されたので、デデキントの定理が示された。(Q.E.D.)
結
今回は、「実数の連続性」の直感的な理解である
- 実数の数直線上には一切”すき間”が無い。
- どんな実数にもその十分近くにまた実数がある。
を皮切りに、「ワイエルシュトラスの上限公理」について解説し、さらにこれが前回解説したデデキントの定理と同値であることを示した。
実数の連続性と同値な命題は合計で6つほどある(他にもある)。
このどれを仮定してもほかが導ける。
次回は、上記2つと同値である「有界な単調列は収束する。」という命題を数列の収束の説明から解説する。
乞うご期待!質問、コメントなどお待ちしております!





コメントをする