絶対見て！「多変数実数値関数の極限の注意」【解析学の基礎シリーズ】多変数関数編 その20

本記事の内容

本記事は、多変数実数値関数の極限についての諸注意を説明する記事です。
本記事を読むにあたり、多変数実数値関数の極限(特に収束)のイメージについて知っている必要があるため、その際は以下の記事を参照してください。
また、今回は多変数実数値関数に対する極限にのみ焦点をあわせます。

「多変数ベクトル値関数の収束」【解析学の基礎シリーズ】多変数関数編 その2

...

for-spring.com

2022.04.29

多変数実数値関数の収束のイメージのチャラい復習

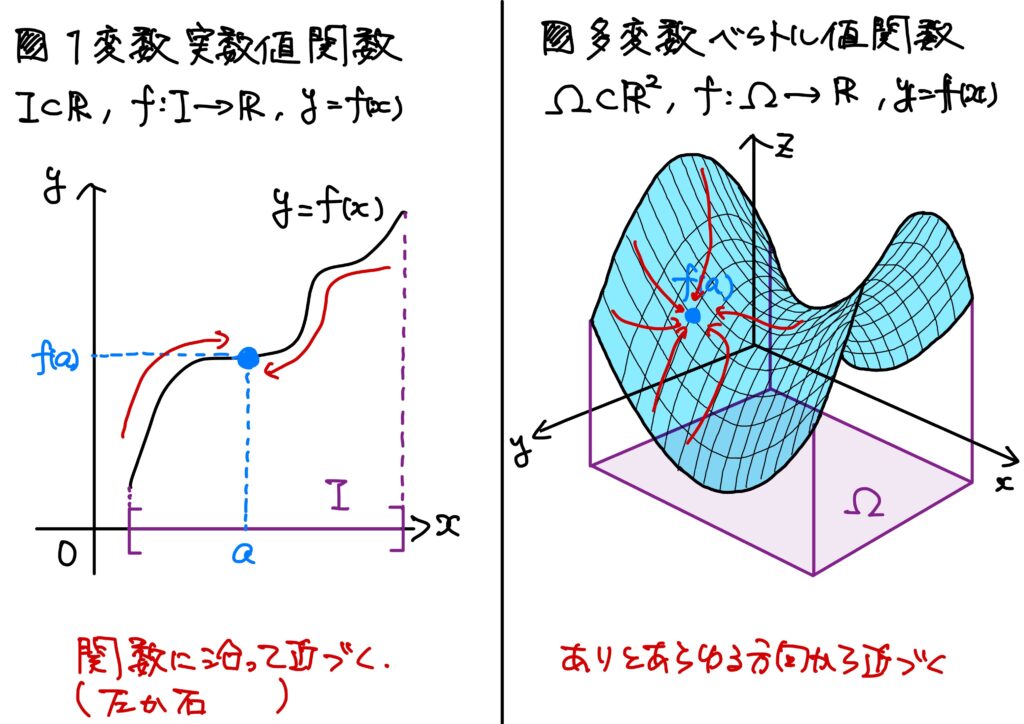
1変数実数値関数の場合の収束と多変数実数値関数の収束のイメージの違いを一言で述べれば、

ということでした。
もっと砕けた言い方をすれば、

ということでした。
模式図としては以下です。

多変数実数値関数の極限への近づき方について

結論から言ってしまえば、

です。
これは、多変数実数値関数(一般に多変数ベクトル値関数)の収束とはどういうことだったかを確認すれば分かります。
多変数ベクトル値関数の収束とは数学的にどういうことだったかというと、

でした。
これを見ると、$\boldsymbol{a}$との距離が$\delta>0$未満という意味で$\boldsymbol{a}$と近い$\boldsymbol{x}\in\Omega$に対して、関数の値$\boldsymbol{f}(\boldsymbol{x})$と$\boldsymbol{A}$との距離が十分近い、ということです。

ということは、$\boldsymbol{a}$と近い$\boldsymbol{x}$に対して$\boldsymbol{f}(\boldsymbol{x})$と$\boldsymbol{A}$が十分近い、というわけですから、どんな経路(近づき方)で近づいたとしても良いということです。

より端的に言えば、「近づき方には一切制限が無い」ということです。
故に、関数の収束というのは経路に依存しないのです。

経路に依存するため、収束しない関数の例

一見収束しそうだけれど、実は収束しないという関数の例を挙げます。
とはいえ、一見収束しそうかなんて個人によりますけどね(笑)

例. $f:\Omega=\mathbb{R}^2\setminus \{(0,0)\}\to\mathbb{R}$を
$$f(x,y)=\frac{xy}{x^2+y^2}\quad ((x,y)\in\mathbb{R}^2\setminus\{(0,0)\})$$
で定めたとします。

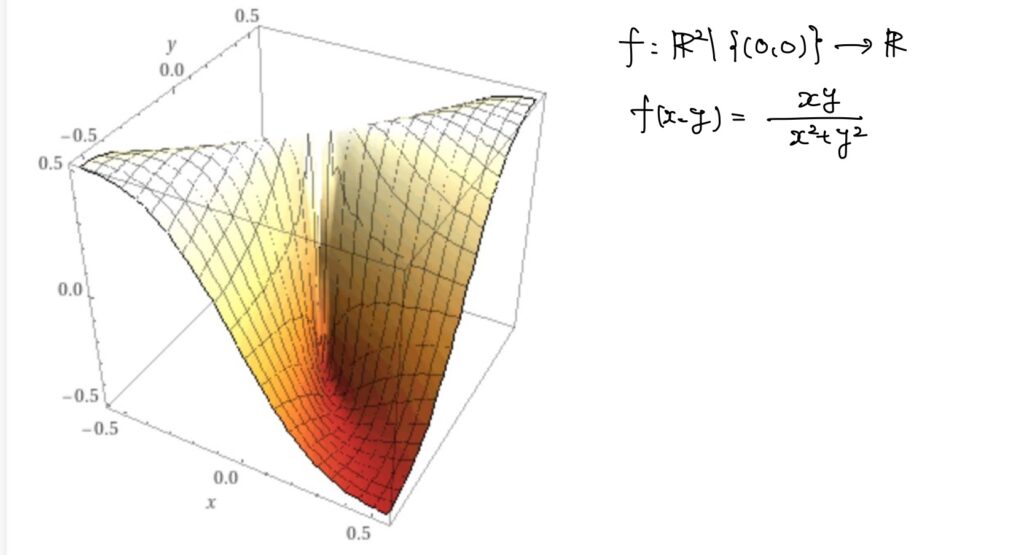
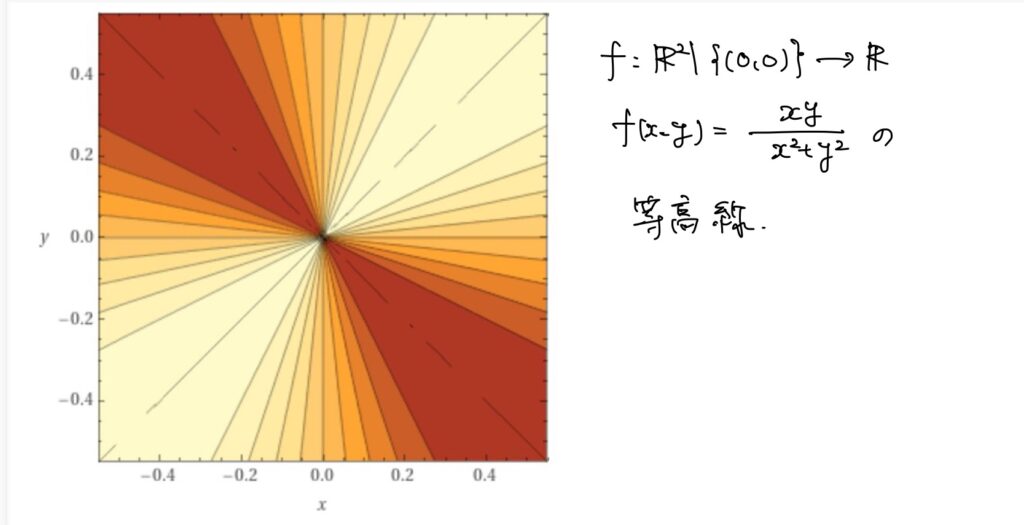
このとき、$\displaystyle\lim_{(x,y)\to(0,0)}f(x,y)$は存在しません。

仮に、$y=kx$という直線に沿った経路でどのように極限に近づくか、どの極限に近づくのかを考えます。
収束するのであれば、経路だったとしても収束先は1つのはずです。
ではやってみましょう。

その前に、経路に沿って近づく、というのは数学的にどういうことかというと、$\Omega_k=\{(x,y)\in\Omega\mid y=kx\}$として、$f|_{\Omega_k}\to\mathbb{R}$を$f|_{\Omega_k}(x,y)=f(x,y)$で定めたとき、$\displaystyle\lim_{(x,y)\to(0,0)}f|_{\Omega_k}(x,y)$を考えるということです。

前回(【解析学の基礎シリーズ】多変数関数編 その19)で証明したとおり、関数が極限を持つのであれば、定義域を制限しても同じ極限へ収束します。
具体的には次です。

すなわち、$\displaystyle\lim_{(x,y)\to(0,0)}f(x,y)=\lim_{(x,y)\to(0,0)}f|_{\Omega_k}(x,y)$です。
しかしながら、
$$\begin{eqnarray} \lim_{(x,y)\to(0,0)}f|_{\Omega_k}(x,y)&=&\lim_{\substack{y=kx \\ (x,y)\to(0,0)}}f(x,y)\\ &=&\lim_{x\to0}f(x,kx)\\ &=&\lim_{x\to0}\frac{x\cdot kx}{x^2+(kx)^2}\\ &=&\lim_{x\to0}\frac{k}{1+k^2}\\ &=&\frac{k}{1+k^2} \end{eqnarray}$$
となり、$(x,y)\to(0,0)$を$y=kx$に沿って極限を取ると、$k$に依存してしまいます。
つまり、収束するのであれば経路によらずに１つの値に収束するはずが、今回は$k$に、いうなれば経路に依存してしまいました。
故に、収束先が１つに定まりません。
従って、収束しないのです。

$\displaystyle\lim_{(x,y)\to)(a,b)}f(x,y)$と、$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$、$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$は別物

前回の最後にチョロっと述べたように、これらは別物です。
先の例に対して考えてみましょう。

例. $f:\Omega=\mathbb{R}^2\setminus \{(0,0)\}\to\mathbb{R}$を
$$f(x,y)=\frac{xy}{x^2+y^2}\quad ((x,y)\in\mathbb{R}^2\setminus\{(0,0)\})$$
で定めたとします。

$$\begin{eqnarray} \lim_{x\to 0}\lim_{y\to 0}f(x,y)&=&\lim_{x\to 0}\lim_{y\to 0}\frac{xy}{x^2+y^2}\\ &=&\lim_{x\to 0}\frac{0}{x^2}\\ &=&\lim_{x\to 0}0=0 \end{eqnarray}$$
です。

一方、
$$\begin{eqnarray} \lim_{y\to 0}\lim_{x\to 0}f(x,y)&=&\lim_{y\to 0}\lim_{x\to 0}\frac{xy}{x^2+y^2}\\ &=&\lim_{y\to 0}\frac{0}{y^2}\\ &=&\lim_{y\to 0}0=0 \end{eqnarray}$$
です。

従って、$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$と$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$には極限は存在します。

しかし、前節でみたとおり、$\displaystyle\lim_{(x,y)\to(0,0)}f(x,y)$は存在しません。
従って別物なのです。

$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$、$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$はいつ使うのかネ？

少々先取り担ってしまうが、偏微分で使います。
偏微分は、多変数の微分法のことを指します。
偏微分は、１つの変数を一旦定数と見て、もう一方の変数の変化量を考える、というわけです。
これはまさに、$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$、$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$を考える、ということになります。

結

今回は、極限が存在しない例について解説しました。
また、$\displaystyle\lim_{(x,y)\to)(a,b)}f(x,y)$と、$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$、$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$は別物だということも示しました。

実は、$\displaystyle\lim_{x\to a}\lim_{y\to b}f(x,y)$と$\displaystyle\lim_{y\to b}\lim_{x\to a}f(x,y)$も別物です。
それは偏微分の単元で話します。

次回は関数の発散の一部について解説します。

乞うご期待！質問、コメントなどお待ちしております！