「有限アーベル群の基本定理の証明①」【代数学の基礎シリーズ】群論編その36

代数学

2023.02.23 2022.12.06

本記事の内容
今回から数回に渡ってやること
有限アーベル群の基本定理は何を言っているのか？
証明の流れ
1. 主張を言い換えてみます。
2. 定理00.(有限アーベル群の基本定理2)の証明の流れ
いざ、証明(Part.1)
追記：証明(Part1)の別証明
皆様のコメントを下さい！
結

本記事の内容

本記事は有限アーベル群の基本定理の証明を順を追って解説する記事です。

本記事を読むに当たり、アーベル群、位数、同型、中国式剰余定理について知っている必要があるため、以下の記事も合わせてご覧ください。

↓アーベル群の記事

↓位数の記事

↓同型の記事

↓中国式剰余定理の記事

今回から数回に渡ってやること

今回から数回に渡って何をするかというと、結論としては、以下の定理を証明します。

定理0.(有限アーベル群の基本定理)

G

$G$ が有限なアーベル群ならば、整数

e_{1}, \dots, e_{n} \geq 2

$e_1,\dots,e_n\geq2$ が存在して、

i = 1, \dots, n - 1

$i=1,\dots,n-1$ に対して

e_{i} | e_{i + 1}

$e_i|e_{i+1}$ を満たし、

$G\cong \mathbb{Z}/{e_1\mathbb{Z}}\times\cdots\times\mathbb{Z}/{e_n\mathbb{Z}}$ となる。また、この条件を満たす

$e_1,\dots,e_n$ は一意的に定まる。ただし、

$n=0$ のときは

$G\cong\left\{0\right\}$ と解釈する。

有限アーベル群の基本定理は何を言っているのか？

要するに、有限アーベル群の基本定理は何を言っているのか、というと

任意の有限アーベル群が巡回群の直積に同型である。

ということです。
もっと平たく言えば、「有限なアーベル群は”いい具合に”商群の直積に分解することができる」ということです。

証明の流れ

主張を言い換えてみます。

$e\geq2$ を整数とすれば、相異なる素数 $p_1,\dots,p_t$ により $e=p_1^{a_1}\cdots p_t^{a_t}$ と素因数分解できます。
ここで、中国式剰余定理を使います。

定理1.(中国式剰余定理)

$m,n\neq 0$ が互いに素な整数ならば、

$\mathbb{Z}/{mn\mathbb{Z}}\cong \mathbb{Z}/{m\mathbb{Z}}\times\mathbb{Z}/{n\mathbb{Z}}$ である。

定理1.(中国式剰余定理)の証明は【代数学の基礎シリーズ】群論編その28を御覧ください。

中国式剰余定理を使うことで、
$\mathbb{Z}/{e\mathbb{Z}}\cong\mathbb{Z}/{p_1^{a_1}\mathbb{Z}}\times\cdots\times\mathbb{Z}/{p_t^{a_t}\mathbb{Z}}$
です。
したがって、有限アーベル群の基本定理の $G$ は位数が素数べきの巡回群の積で表されることになります。
そこで、有限アーベル群の基本定理の代わりに、次の定理を証明することにします。
その証明の跡で、有限アーベル群の基本定理が以下の定理から従うことを示します。

定理00.(有限アーベル群の基本定理2)

$G$ を有限なアーベル群とするとき、次の1.、2.が成り立つ。

素数 $p_1,\cdots,p_t$ (重複を許す)と正の整数 $a_1,\cdots,a_t$ が存在して $\mathbb{Z}/{e\mathbb{Z}}\cong\mathbb{Z}/{p_1^{a_1}\mathbb{Z}}\times\cdots\times\mathbb{Z}/{p_t^{a_t}\mathbb{Z}}$ となる。また、 $p_1^{a_1},\cdots,p_t^{a_t}$ は順序を除いて一意的に定まる。
素数 $p$ に対して、 $G(p)$ を $p_i=p$ である $i$ 全てに属する $\mathbb{Z}/{p_i^{a_i}\mathbb{Z}}$ の直積とすると、 $G$ は全ての $G(p)$ の直積であり、 $G(p)$ は $G$ のシロー $p$ 部分群である。

定理00.(有限アーベル群の基本定理2)の証明の流れ

同型写像の存在
1. $\left|G\right|$ が $p$ ベキであることの証明→今回
2. $G$ が巡回群の直積となることの証明
3. 同型写像を作る。
存在する整数の一意性
1. 上の分解が直積因子の順序を除き一意的であることの証明
2. 一般の場合の直積因子の一意性の証明

今回は1.-1.を示します。

いざ、証明(Part.1)

群 $G$ の演算は加法的に $+$ と書き、単位元も $0$ と書くことにします。

$\left|G\right|=n=p^am$ とします。
ただし、 $p$ は素数、 $a>0$ で、 $p$ と $m$ は互いに素とします( $m=1$ の場合も含みます)。

$g\in G$ とすると、位数がそれぞれ $p^a$ 、 $m$ の約数の要素 $x,y$ が存在して、 $g=x+y$ と書けることを示します。
$p^a,m$ は互いに素なので、 $p^a\alpha＋m\beta=1$ となるような整数 $\alpha,\beta$ が存在します。
$x=m\beta g$ 、 $y=p^a\alpha g$ とすると、
$g=\left( p^a\alpha+m\beta\right)g=x+y$
となり、
$p^ax=n\beta g=0,\quad my=n\alpha g=0$
です。
よって、 $x,y$ の位数はそれぞれ $p^a,m$ の約数です。

$H=\left\{x\in G\middle| p^ax=0\right\},\quad K=\left\{x\in G\middle|mx=0\right\}$
とすると、 $H,K$ は部分群です。
$z\in H\cap K$ ならば、 $p^az=mz=0$ なので、 $z=\left( p^a\alpha+m\beta\right)z=0y$ となります。
故に、 $H\cap K=\left\{0\right\}$ です。
ここで、次の事実を使います。

命題2.

$G$ が群、

$H,K\subset G$ が正規部分群で

$H\cap K=\left\{ 1_G\right\}$ 、

$HK=G$ とする。このとき、

$G$ は直積

$H\times K$ と同型である。

命題2.の証明は【代数学の基礎シリーズ】群論編その28を御覧ください。

先程、 $H+K=G$ となることを証明したので、命題2.から $G\cong H\times K$ です。

追記：証明(Part1)の別証明

別証明をご紹介します。

今回証明することを主張の形で明示すると、以下になります。

命題3.

有限なアーベル群

$G$ の位数

$\left|G\right|$ が

$\left|G\right|=p_1^{a_1}\cdots p_m^{a_m}$ \quad (ただし、

$p_t$ は相異なる素数)

と素因数分解されるとし、

$G$ のシロー

$p_t$ 部分群を

$G(p_t)$ で表す。このとき、

$G\cong G(p_1)\times \cdots\times G(p_m)$ である。

命題3.の証明

群 $G$ はアーベル群というだけなので、演算はどのように書いてもOKです。
ここでは、表記の見てくれが(個人的に)スッキリしていると思う加法 $+$ を使うことにします。

クドいようですが…

群

$G$ の演算を加法的に表すということは、

$x,y\in G$ に対して、

$x$ と

$y$ に演算を施した結果を

$x+y$ と書く、という意味です。

証明は、 $m$ に対する数学的帰納法で証明します( $m$ は $\left|G\right|$ の素因数の数)。

$m=1$ のときは、そもそも $\left|G\right|$ が素数のベキになるということ、つまりは $G$ 自身がシロー部分群になってしまう、ということなのでOKです。

ここで、
$L=\left\{x\in G\middle|\left( p_2^{a_2}\cdots p_m^{a_m}\right)x=0\right\}$
とします。
条件式 $\left( p_2^{a_2}\cdots p_m^{a_m}\right)x=0$ は、「 $x$ を $p_2^{a_2}\cdots p_m^{a_m}$ 回足す」という意味です。

ちなみに、群の演算を $+$ でなく $\times$ とすれば…

$L=\left\{x\in G\middle|x^{p^a}=1\right\}$ となります。

① $L$ は $G$ の部分群

$\left( p_2^{a_2}\cdots p_m^{a_m}\right)0=0$ となるため、 $0\in L$ です。

任意の $x,y\in L$ に対して、

$\left( p_2^{a_2}\cdots p_m^{a_m}\right)(x+y)= \left( p_2^{a_2}\cdots p_m^{a_m}\right)x+\left( p_2^{a_2}\cdots p_m^{a_m}\right)y =0+0=0$
$\left( p_2^{a_2}\cdots p_m^{a_m}\right)=(-x)=- \left( p_2^{a_2}\cdots p_m^{a_m}\right)x=-0=0$

となります。
したがって、 $x+y\in L$ かつ $-x\in L$ です。

② $\left|L\right|= p_2^{a_2}\times\cdots \times p_m^{a_m}$

各 $t\geq2$ に対して、 $G(p_t)\subseteq L$ です。
実際、 $G(p_t)$ は位数が $p_t^{a_t}$ の群であるため、任意の $z\in G(p_t)$ に対して $\left( p_t^{a_t}\right)z=0$ となるから、 $G(p_t)$ は $L$ の部分群です。

また、①により $L\subset G$ だから、 $G(p_t)\subseteq L\subset G$ となります。
ここで、ラグランジュの定理の系を使います。

系4.

$G$ を有限群とするとき、次の1.、2.が成り立つ。

$H$ が $G$ の部分群ならば、 $\left|H\right|$ は $\left|G\right|$ の約数である。
$g\in G$ の位数は $\left|G\right|$ の約数である。

系4.の証明は【代数学の基礎シリーズ】群論編その15を御覧ください。

系4.から $\left|L\right|$ は $G(p_2)$ の位数、 $G(p_3)$ の位数、…、 $G(p_m)$ の位数、すなわち $p_2^{a_2}$ 、 $p_3^{a_3}$ 、…、 $p_m^{a_m}$ のすべてを約数に持ちます。
したがって、
$\left|L\right|=p_1^{c_1}\cdot p_2^{a_2}\cdots p_m^{a_m}$
という形しかありえない、ということになります。
では「 $c_1$ は？」という話ですが、仮に $c_1\geq 1$ だったとすると、 $\left|L\right|$ の素因数として $p_1$ が出現することになります。

ここで、次の事実を使います。

命題5.

$\left|G\right|$ の素因数

$p$ に対して、

$G$ は位数

$p$ の要素を含む。

命題5.の証明は後日行い、本文に明示します。

さて、命題5.を認めれば、 $L$ は位数 $p_1$ の要素を含まなければいけません。
しかしながら、位数 $p_1$ の要素は $p_1$ の倍数でない限りは $0$ になりえません。
故に、 $c_1=0$ でなければなりません。
したがって、
$\left|L\right|=p_2^{a_2}\cdots p_m^{a_m}$
ということになります。

すると、帰納法の仮定が使えて、 $L\cong G(p_2)\times \cdots\times G(p_m)$ となります。

③ $G\cong G(p_1)\times L$

もしこれが示されれば、 $G\cong G(p_1)\times \cdots\times G(p_m)$ となります。
さて、 $\varphi:G(p_1)\times L\longrightarrow G$ を $\varphi(x,y)=x+y$ で定めます。
ちなみに、 $x\in G(p_1)$ 、 $y\in L$ ですが、 $P_1\subseteq L\subset G$ であるため、 $x,y\in G$ だから和を取ることができます。

$G$ はアーベル群ですので、 $\varphi$ は群の準同型写像です。
もし、この $\varphi$ が単射であれば、 $\varphi$ は有限集合から有限集合への写像であって、しかも、双方の要素の数が(今回は位数) $p_1^{a_1}\cdots p_m^{a_m}$ で一致しているため、全射でもあります。
すなわち、 $\varphi$ が全単射ということになり、 $\varphi$ は同型写像となるわけです。

そこで、 $\varphi$ の単射性を証明します。

$(x,y)\in{\rm Ker}(\varphi)$ とすると、 $\varphi(x,y)=x+y=0$ 、つまり $x=-y$ です。
今、 $x\in G(p_1)$ であり $y\in L$ であるため、 $x=-y\in G(p_1)\cap L$ です。

再度系4.から $G(p_1)$ の位数は、 $p_1^{a_1}$ の約数であり、 $L$ の要素の位数は $p_1^{a_1}\cdots p_m^{a_m}$ の約数です。
つまり、位数が $1$ ということです。
位数が $1$ ということは、 $x,y$ はともに単位元、すなわち $(x,y)=(0,0)$ です。
故に、任意の $(x,y)\in{\rm Ker}(\varphi)$ が $(x,y)=(0,0)$ ということから、 ${\rm Ker}(\varphi)$ は単位元のみからなる集合だ、ということがわかります。

ここで、次の事実を思い出します。

定理6.

準同型写像

$\phi:G_1\longrightarrow G_2$ が単射であるための必要十分条件は、

${\rm Ker}(\phi)=\left\{1_{G_1}\right\}$ となることである。

定理6.の証明は【代数学の基礎シリーズ】群論編その3を御覧ください。

定理6.から、 $\varphi$ は単射です。
$\varphi$ の定義域と値域の要素の数(今回は位数)を確認すれば、ともに
$p_1^{a_1}\cdots p_m^{a_m}$
となっています。
そして、 $\varphi$ は有限集合から有限集合への写像であって、しかも要素の数が一致しているような単射であるから、全射でもあります。
故に、 $\varphi$ は全単射のため、 $\varphi$ は同型写像です。

したがって、 $G\cong G(p_1)\times L$ となります。

命題3.の証明終わり

ちなみに

この部分の証明は龍孫江様の証明を参考にさせていただいております。

皆様のコメントを下さい！

数回に渡って、古代ギリシャで生まれた数学(特に幾何学)がデカルトの出現により大きく変化したということについて少々語ります。

前回は、記法により数学が、特に代数が質的に変化した、という話をしました。

幾何学的量の演算の制限を取り除き、幾何学の問題を代数的に捉えてそれを記号を用いて解くことは、フランスの哲学者であり数学者であったデカルトにより行われました。
デカルトは、「方法序説」(1637)の中で、単位の長さ(数の $1$ に当たる)を固定し、2つの線分の掛け算と割り算を、その結果が再び線分となるように定めたのです(図では $1$ が単位の長さを持つ線分を表します。)
その際、比例の理論が重要な役割を果たしました。

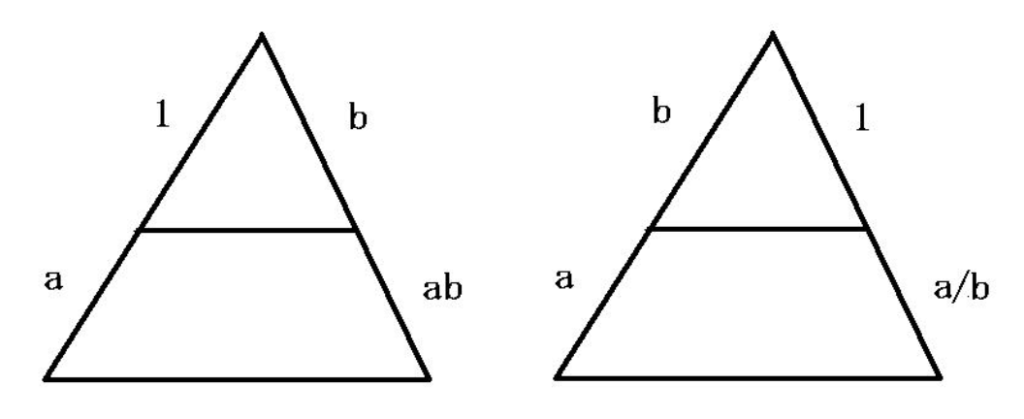
直線 $l$ を固定し、その上に2点 $O$ と $E$ を取ります。
このとき $OE$ を単位の線分とすることにより、 $l$ は加減乗除の演算を持つ系(代数系)と考えることができます。
例えば、 $A,B$ を $l$ の点とするとき、 $l$ の点 $C,D$ を $OC=OA+OB$ 及び $OD=OA\cdot OB$ となるようにそれぞれ選び、足し算 $A+B$ の結果を $C$ 、掛け算 $A\cdot B$ の結果を $D$ として定めれば、加法と乗法が直線 $l$ 上で定められます。
減法、除法も同様にして定められます。
さらに平方根も定めることが可能であり、このことから直線と円の交わりを求める問題は2次方程式に帰着します。
特別な点 $O,E$ はそれぞれ数における $0$ と $1$ の役割を果たしています。

この固定された直線 $l$ により、ユークリッド幾何学の問題はすべて代数の問題に帰着すること、これがデカルトが考えたことなのです。

今回はここまで。
感想など是非コメントをお待ちしています！

結

今回は、有限アーベル群の基本定理の証明の一部を解説しました。
有限アーベル群の基本定理は、「任意の有限アーベル群が巡回群の直積に同型である」という主張の定理です。
つまり、極端に言えば有限で、かつ可換な群であれば”いい具合に”商群の直積に分解できる、ということです。

次回は今回の続きとして、 $G$ が巡回群の直積となることの証明を行います。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ一週間以内にお答えします。

コメントをする

名前:naru : 投稿日：2023/02/12(日) 18:51:26 ID：E4MDMwNTY

H={x∈G│p^ax=0}なら│H│=p^aではないでしょうか。後半で、│H│がpべきでなければ、とあるのはどうしてでしょうか。ここでは群を加法的に考えているのですよね。

返信

名前:naru : 投稿日：2023/02/13(月) 15:43:39 ID：M1OTAwOTY

H={x∈G│p^ax=0}なら│H│=p^aではないでしょうか。
この主張は、ヤフー知恵袋での、同じ雪江先生の教科書で、K={x∈G│mx=0}に対して│K│=mと回答者が答えているのを踏まえています。
リンクを貼っておきます。

https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13268734493?__ysp=6Zuq5rGf44CA44Ki44O844OZ44Or44CA5Z%2B65pys5a6a55CG

返信

名前:オノコウスケ : 投稿日：2023/02/14(火) 01:53:31 ID：E3ODk5MzY

naru様

まとめてお答えします。

まず、
>H={x∈G│p^ax=0}という表記がわかりにくいです。加法的ではなく乗法的に表すとH={g∈G│g^n=0}みたいな感じなのでしょうか。でもこれは巡回群を表しているとは言えないし…
とのご指摘ですが、群 $G$ の演算を加法的に書いたのは、今回の場合は乗法的に書くよりも加法的に書く方がスッキリとした表現だと感じているからです。
もちろん、加法的でなければならないわけではありません。
ちなみに、 $p^ax=0$ の意味は、「 $x$ を $p^a$ 回足し合わせたもの(今回の $G$ の演算は加法としている為)が $0$ と等しい」という意味であり、これをあえて乗法的に表すとするならば、「 $x$ を $p^a$ 回掛け算して単位元と等しい」ということですので、 $H=\left\{x\in G\middle|x^{p^a}=1\right\}$ という表記になります。
このように書いてしまうと、 $x$ の肩に更に指数が乗ることになり、表記としてあまり見やすくないと感じています。
これは好き好きですので、本ブログではこの表現(つまり加法的な表現)のままとさせていただきます。

次に、
>H={x∈G│p^ax=0}なら│H│=p^aではないでしょうか。
とのご質問ですが、結論から申し上げて、おっしゃる通りです。
証明の該当部分、すなわち「 $\left|H\right|$ が $p$ べきでなければ、…」の部分は、結局の所、 $\left|H\right|$ が $p$ べきであることを証明しています。
naru様は
$H=\left\{x\in G\middle|p^ax=0\right\}$
を見た瞬間、「 $\left|H\right|=p^a$ だから $\left|H\right|$ は $p$ べきだよね」と直ちにお思いになったのではないでしょうか。
そのため、「なぜあえて $\left|H\right|$ が $p$ べきでない場合を考える必要があるのか？」という考えに至ったのではないでしょうか。
本ブログの文章としては、 $H$ を定た後に「 $H$ が $p$ べきである」ということを「 $\left|H\right|$ が $p$ べきでないならば…」と背理法で証明している、というわけです。

P.S. たしかにこの記事の証明はあまり分かりやすいとは言えないかもしれませんので、他の方の別証明を追記致します。

返信

名前:naru : 投稿日：2023/02/13(月) 10:19:39 ID：M1OTAwOTY

H={x∈G│p^ax=0}という表記がわかりにくいです。加法的ではなく乗法的に表すとH={g∈G│g^n=0}みたいな感じなのでしょうか。でもこれは巡回群を表しているとは言えないし…

返信
名前:naru : 投稿日：2023/02/14(火) 06:56:55 ID：UzNzcyNTU

H={x∈G│p^ax=0}という表記は何を表しているのでしょうか。ここで、3次対称群の乗法的な場合を考えてみます。
H={σ∈S_3│σ^2=1}とします。
すると、H={(1)、(12)、(13)、(23)}となり、これはGの部分群とは言えないのではありませんか。

返信

名前:オノコウスケ : 投稿日：2023/02/16(木) 01:38:23 ID：c2NzU4NDI

naru様

①>H={x∈G│p^ax=0}という表記は何を表しているのでしょうか。
とのことでしたが、これは以前お答えしている通りです。
$p^ax=0$ の意味は、「 $x\in G$ を $p^a$ 回足し合わせたもの(今回の $G$ の演算は加法としている為)が $0$ (単位元)と等しい」という意味です。

ちなみに

これをあえて乗法的に表すとするならば、「 $x$ を $p^a$ 回掛け算して単位元と等しい」ということですので、 $H=\left\{x\in G\middle|x^{p^a}=1\right\}$ という表記になります。

したがって、 $H=\left\{x\in G\middle|p^ax=0\right\}$ は「 $H$ は、 $p^a$ 回だけ足し合わせたときに単位元と一致するような $x\in G$ の集合である」という意味になります。
今回は群 $G$ の演算を加法としておりますので”足し合わせた”という表現を使っていますが、群 $G$ の演算を加法としないのであれば、「 $H$ は、 $x\in G$ に $x$ 自身を $p^a$ 回だけ $G$ の演算で施したとき、 $G$ の単位元と一致するような $x\in G$ の集合である」と言うこともできます。

②>H={σ∈S_3│σ^2=1}とします。すると、H={(1)、(12)、(13)、(23)}となり、これはGの部分群とは言えないのではありませんか。
とのことでしたが、まず、この記事で扱っている群はそもそもアーベル群(可換群)です。
対称群は一般にアーベル群ではありません(簡単に確かめられます)。
したがって、対称群は有限アーベル群の基本定理の理解のための例にはなりえないということを、ご注意下さい。
さて、集合 $G$ および $H$ を
$G=\mathcal{S}_3$
(すなわち、3次の対称群)、および
$H=\left\{\sigma\in G=\mathcal{S}_3\middle|\sigma^2=1\right\}$
で定めます。
ただし、 $\sigma^2$ は $\sigma$ と $\sigma$ 自身の合成写像 $\sigma\circ \sigma$ を、 $1$ は $\left\{1,2,3\right\}$ から $\left\{1,2,3\right\}$ 自身への恒等写像を表します。
このとき、naru様のご指摘の通り、
$H=\left\{(1),\ (1\ 2),\ (1\ 3),\ (2\ 3)\right\}$
となり、 $H$ は $G=\mathcal{S}_3$ の部分群とはなりえません(実際、 $(1\ 2)(1\ 3)\not\in H$ )。
本記事において考察している群 $G$ は、アーベル群であるため、 $H$ が $G$ の部分群となります(簡単に確かめられます)。
つまり、何がいいたいかと言うと、

言いたいこと
$G=\mathcal{S}_3$ 、 $H=\left\{\sigma\in G=\mathcal{S}_3\middle|\sigma^2=1\right\}$ のときは $H$ は $G$ の部分群にはならない。
しかし、本記事では $G$ がアーベル群でるため $H=\left\{x\in G\middle|p^ax=0\right\}$ (ただし $G$ の演算は和と捉えている)は $G$ の部分群となる。

ということです。

返信

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34