本記事の内容
本記事は、生成元と関係式で定義された群とその性質について解説する記事です。
本記事を読むに当たり、自由群について知っている必要があるため、以下の記事も合わせて御覧ください。
各種軽い復習
対称群
は写像の合成を演算として群でした。
この\(\mathcal{S}_X\)は特別な呼び名があり、置換群、または対称群と呼びます。
これは、まさに以前線型代数の記事で解説した置換が、写像の合成でもって群であるということです。
置換とは以下でした。
置換
\(n\in\mathbb{N}\)とする。\(n\)個の文字\(1,2,\dots,n\)からなる集合を $$ M_n=\{1,2,\dots,n\} $$ とする。写像\(\sigma:M_n\to M_n\)が全単射であるとき、\(\sigma\)を\(M_n\)の置換という。置換\(\sigma\)による対応が $$ 1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n $$ であるとする、すなわち、 $$ \sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n $$ とする。このとき\(\sigma\)を $$ \sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix} $$ と書く。
生成された部分群
定理1.
\(\langle S\rangle\)を\(S\)の要素による語全体の集合とするとき、次の1.、2.が成り立つ。- \(\langle S\rangle\)は\(G\)の部分群である。
- \(H\)が\(G\)の部分群で\(S\)を含むならば、\(\langle S\rangle\subset H\)である。すなわち、\(\langle S\rangle\)が\(S\)を含むような最小の部分群である。
定理1.の証明は【代数学の基礎シリーズ】群論編 その2を御覧ください。
定理1.の\(\langle S\rangle\)のことを\(S\)によって生成された部分群、\(S\)のことを生成系、\(S\)の要素を生成元といいます。
これをまとめると、次です。
生成された部分群、生成系、生成元
\(\langle S\rangle\)を\(S\)の要素による語全体の集合とするとき、\(\langle S\rangle\)を\(S\)によって生成された部分群、\(S\)のことを生成系、\(S\)の要素を生成元という。自由群
自由群
- 語 \(n\)個の変数を\(x_1,\dots,x_n\)と書く。\(x_1,\dots,x_n\)の長さ\(m>0\)の語とは、\(\left\{1,\dots,m\right\}\)から $$ \left\{1,\dots,n\right\}\times\left\{1,-1\right\}=\left\{(1,1),(1,-1),\dots,(n,1),(n,-1)\right\} $$ への写像のことと定める。この写像の\(1,\dots,m\)での値が\((i_1,p_1),\dots,(i_m,p_m)\)なら(\(p_1,\dots,p_m=\pm1\))、この要素を $$ x_{i_1}^{p_1}\dots x_{i_m}^{p_m} $$ と書く。\(x_1,\dots,x_n\)の長さ\(0\)の語は一つだけあると定め、それを\(1\)と書く。
- 縮約 \(W_{n,m}\)を\(x_1,\dots,x_n\)の長さ\(m\)の語の集合として、 $$ W_n=\coprod_{m=0}^\infty W_{n,m} $$ と定める。\(W_{n}\)の要素\(x_{i_1}^{p_1}\dots x_{i_m}^{p_m}\)が途中で\(x_ix_i^{-1}\)または\(x_i^{-1}x_i\)という表現を含むならば、その部分を除いて新たな語を得ることを語の縮約という。
- 自由群 語\(y_1,y_2\)が両方を縮約して(何もしないことも含みます)同じ語になるとき、\(y_1,y_2\)は同値であるという。これは同値関係になる。\(W_n\)に対してこの同値関係における商集合を\(F_n\)と書く。\(F_n\)の任意の要素\(y\)に対して、\(y1=1y=y\)と定める。長さ\(m,l>0\)の語 $$ y_1=x_{i_1}^{p_1}\dots x_{i_m}^{p_m},\quad y_2=x_{j_1}^{q_1}\dots x_{j_l}^{q_l}\in W_n $$ を代表元に持つ\(F_n\)の2つの要素に対して、その積を $$ x_{i_1}^{p_1}\dots x_{i_m}^{p_m}x_{j_1}^{q_1}\dots x_{j_l}^{q_l}\in W_n $$ を代表元にもつ\(F_n\)の要素とする。これは代表元のとり方によらずに定まるため、\(F_n\)の演算となる。この演算により\(F_n\)は群となる。この群\(F_n\)を\(n\)変数の自由群という。
生成元と関係式で定義された群
まずは具体例とそのイメージから
例えば、対称群\(\mathcal{G}_3\)は、\(\sigma=(1\ 2\ 3)\)、\(\tau=(1\ 2)\)という2つの要素から生成され、\(\sigma^3=\tau^2=1\)、\(\tau\sigma\tau=\sigma^{-1}\)という関係式を満たします。
しかし、例えば自明な群\(H=\left\{1\right\}\)で\(\sigma=\tau=1\)としても同じ関係式を満たします。
つまり、
という問題意識から来ているのが、生成元と関係式で与えられた群なのです。
そして、生成元と関係式で与えられた群がそれを実現しているのです。
生成元と関係式で定義された群の数学的な説明
\(F_n\)を\(n\)変数\(\boldsymbol{x}=\left( x_1,\dots,x_n\right)\)の自由群、\(R_1(\boldsymbol{x}),\dots,R_m(\boldsymbol{x})\)を有限個の\(F_n\)の要素とします。
このとき、
$$
S=\left\{gR_i(\boldsymbol{x})g^{-1}\middle|g\in F_n,\ i=1,\dots,m\right\},\quad N=\ \langle S\rangle
$$
とします。
このとき、以下の事実を使います。
系2.
\(G\)を群、\(S\subset G\)とする。このとき $$ N=\langle \left\{xyx^{-1}\middle|x\in G\ y\in S\right\}\rangle $$ は\(S\)を含む最小の\(G\)の正規部分群である。この系2.から、\(N\)は\(R_1(\boldsymbol{x}),\dots, R_m(\boldsymbol{x})\)を含む最小の正規部分群です。
生成元と関係式で定義された群
\(F_n/{N}\)を\(\left\langle x_1,\dots,x_n\middle| R_1(\boldsymbol{x})=1,\dots,R_m(\boldsymbol{x})=1\right\rangle\)と書き、生成元\(x_1,\dots,x_n\)と関係式\(R_1(\boldsymbol{x})=1,\dots,R_m(\boldsymbol{x})=1\)で定義された群という。\(x_1,\dots,x_n\)の\(F_n/{N}\)における像も、記号を乱用してしまいますが\(x_1,\dots,x_n\)と書きます。
なお、変数は\(x_1,\dots,x_n\)でなくても同じです。
また、\(\tau\sigma\tau=\sigma^{-1}\)というような関係式は\(\tau\sigma\tau\sigma=1\)として解釈します。
例えば、
$$
\left\langle x,y\middle|x^3=y^2=1,\ yxy=x^{-1}\right\rangle=\left\langle x,y\middle| x^3=y^2=!,\ yxyx=1\right\rangle
$$
とみなす、ということです。
生成元と関係式で定義された群の性質
\(R(\boldsymbol{x})\)が語、\(G\)が群で\(y_1,\dots,y_n\in G\)とします。
このとき、次の事実を使います。
定理3.
\(G\)を群、\(g_1,\dots,g_n\in G\)とする(\(g_1,\dots,g_n\)には重複があっても良い)。このとき、\(n\)変数の自由群\(F_n\)から\(G\)への、\(\varphi(x_i)=g_i\)が任意の\(i=1,\dots,n\)に対して成り立つような準同型\(\varphi\)がただ一つ存在する。定理3.の証明は【代数学の基礎シリーズ】群論編 その29を御覧ください。
定理3.により、\(x_1,\dots,x_n\)に\(y_1,\dots,y_n\)を代入した\(G\)の要素\(R(y_1,\dots,y_n)\in G\)を考えることができます。
先程定めた群は次の性質を持ちます。
定理4.
\(G\)は\(n\)個の生成元\(y_1,\dots,y_n\)を持ち、関係式 $$ R_1(y_1,\dots,y_n)=\dots=R_m(y_1,\dots,y_n)=1_G $$ を持つとする。このとき、 $$ K=\left\langle x_1,\dots,x_n\middle|R_1(\boldsymbol{x})=1,\ \dots,R(\boldsymbol{x})=1\right\rangle $$ から\(G\)への、\(\varphi(x_1)=y_1,\cdots,\varphi(x_n)=y_m\)を満たす全射準同型\(\varphi\)が存在する。定理4.の証明
\(S,N\)は先程定めた
$$
S=\left\{gR_i(\boldsymbol{x})g^{-1}\middle|g\in F_n,\ i=1,\dots,m\right\},\quad N=\ \langle S\rangle
$$
とします。
定理3.から、\(\psi(x_1)=y_1,\dots,\psi(x_n)=y_n\)を満たす準同型写像\(\psi:F_n\longrightarrow G\)が存在します。
\(G\)は\(y_1,\dots,y_n\)で生成されているわけですので、\(\psi\)は全射です。
\(G\)では\(R_1(y_1,\dots,y_n)=\dots=R_m(y_1,\dots,y_n)=1_G\)が成り立つので、\(R_1(\boldsymbol{x}),\dots,R_m(\boldsymbol{x})\in{\rm Ker}(\psi)\)です。
\({\rm Ker}(\psi)\)は\(F_n\)の正規部分群なので、\(S\subset {\rm Ker}(\psi)\)です。
故に、\(N\subset {\rm Ker}(\psi)\)です。
ここで、次の事実を使います。
定理5.(準同型の分解)
\(\varphi:G\longrightarrow H\)を群の準同型とする。\(N\subset G\)が正規部分群なら、\(\pi:G\longrightarrow G/{N}\)を自然な準同型とするとき、下図が可換図式となるような準同型\(\psi:G/{N}\longrightarrow H\)が存在するための必要十分条件は\(N\subset {\rm Ker}(\varphi)\)となることである。
定理5.の証明は【代数学の基礎シリーズ】群論編 その8を御覧ください。
定理5.から、\(\pi:F_n\longrightarrow K\)を自然な全射とするとき、\(\psi=\varphi\circ \pi\)となる準同型写像\(\varphi:K\longrightarrow G\)が存在します。
\(\psi\)が全射なので、\(\varphi\)もまた全射であり、\(\psi(x_i)=y_i\)なので、\(\varphi(x_i)=y_i\)です。
定理4.の証明終わり
補足情報
軍が生成元と関係式で与えられることは「トポロジー」などでよくあることという印象があります(専門ではないので偏見かもしれませんが)。
その場合には群の位数が有限なのか、無限なのか、もし有限であればその位数は何か?ということが基本的な問題です。
一般には「トッド-コクセターの方法」というものが知られていて、これに対する完全な答えを与えることができます(ここでは述べません)。
簡単な場合には、群の位数が何か以下になるということは比較的容易にわかりますが、問題なのは、群の位数が何か以上になる、ということを示す部分です。
皆様のコメントを下さい!
今回から数回に渡って、幾何学の歴史について少々語ろうと思います。
我々が学校で学んだ幾何学は古代ギリシャで確立した理論であり、その多くの定理はピタゴラス学派によって証明されました。
「三角形の内角の和は\(180^\circ\)」という定理と三平方の定理がその代表です。
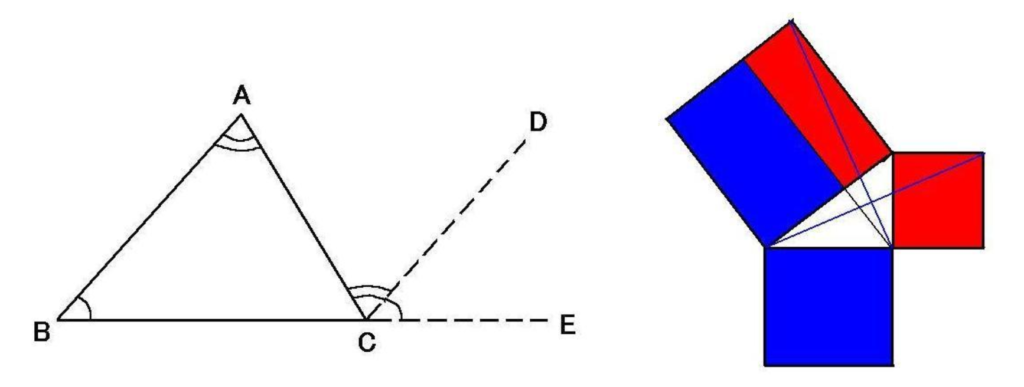
補助線\(CD\)は辺\(AB\)に平行だとします。
内角の和が\(180^\circ\)であるということは、平行線の性質である「錯覚は等しい」、「同位角は等しい」ことから導かれます。
三平方の定理は「面積の移動」で証明されます。
下の図を見ると、使うのは「三角形のの面積は底辺と高さで決まる」ことと、三角形の合同定理(二辺狭角)です。

内角の和定理と三平方の定理は「紙の上」での事実ではありますが、宇宙空間の構造を研究する一般相対論と、曲がった空間を研究する現代幾何学に密接に関連しています。
以前ピタゴラス学派を紹介した際に述べたと思いますが(述べてなかったらごめんなさい)、ピタゴラス学派は全ての線分が互いに「通訳的」、つまり線分の長さの比は常に有理数だと信じていました。
4つの線分\(\alpha_1,\beta_1,\alpha_2,\beta_2\)について\(\alpha_1:\beta_1=\alpha_2:\beta_2\)が成り立つのは、ある自然数\(m,n\)が存在して
次の定理は幾何学に置いて基本的な役割を担っています。
ただし、全ての線分は通訳的だとします。
\(\triangle ABC\)の辺\(AB\)上の点\(D\)から辺\(BC\)に塀行こうな直線を引き、辺\(AC\)との交点を\(E\)とする。このとき $$ AD:DB=AE:EC $$ である。
しかしながら、ピタゴラス学派が証明した三平方の定理によれば、直角二等辺三角形の斜辺と他の辺の比は通訳的ではありません。
実際、\(a\)を斜辺の長さとして、他の辺の長さを\(1\)とすると、\(1^2+1^2=a^2\)、つまり\(a^2=2\)となって、\(a\)は有理数ではありません。
したがって、ピタゴラス学派の幾何学は破綻してしまいました。
この「危機」を救ったのがユードクソスです。
ユードクソスの理論は、19世紀になってデデキントによる実数の厳密な理論に繋がります。
結
今回は生成元と関係式で定義された群について解説しました。
この群は「ある生成元を持ち、それが与えられた関係式を満たすような群の中で最大のもの」です。
似たようなものとして、最小の正規部分群というものがありましたが、考え方によってはある種その対比のようなものです。
次回は今回解説した群の例題として、実際にどのように使うか、ということを述べます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
代数についてより詳しく知りたい方は以下を参考にすると良いと思います!




コメントをする