本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
では、問題
1. 格子点とは、平面上で座標がいずれも有理整数である点を意味することにします。このとき、\(n\)個(\(n\geq5\))の格子点を頂点とする凸\(n\)角形の辺および対角線全部を書くと、頂点以外の格子点で、それらの辺または対角線の上にあるものが存在することを証明して下さい。
2. 上の問題で、格子点の意味を、次のように変えた場合は、どうなるかを考え、それを証明して下さい。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p17.
平面を、下の図のように1辺の長さ1の正三角形に分割したときの頂点全体を格子点とする。
いざ、チャレンジ
チャレンジの結果…解けました。
この問題は真正直に解こうとすると計算量が膨大になってしまいますが、あるグループ分けをすることで比較的簡単に証明できる問題だ思います。
筆者の回答
では、筆者の回答を紹介します。
まずは、実験
まずは、問題文の主張が本当に成り立ちそうか、ということを確かめてみました。
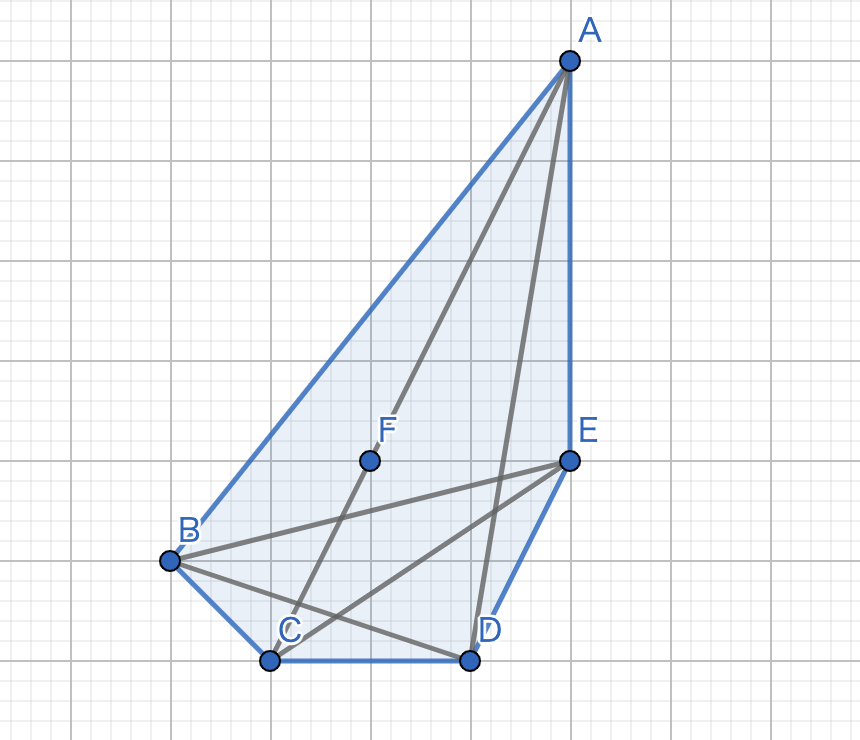
点\(F\)の座標がたしかに有理整数ですので、どうやら成り立ちそうです。
真正直に解こうとした回答(答えにはたどり着かなかったため、読み飛ばしてOK)
先程、「真正直に解こうとすると計算量が膨大」という話をしましたが、筆者は最初真正直に解こうとしました。
まずはその回答を紹介します。
問題文曰く、格子点とは
と定められています。
これを数式に起こします。
平面上の格子点の集合を\(L^\prime\)とすると、
と書けます。
しかし、今回はここまで一般化する必要はないと思われますので、
\(\displaystyle\boldsymbol{x}_1=\boldsymbol{e}_1=\left(\begin{array}{c}1\\0 \end{array}\right)\)、\(\displaystyle\boldsymbol{x}_2=\boldsymbol{e}_2=\left(\begin{array}{c}0\\1 \end{array}\right)\)、とします。
すなわち、今回考える格子点の集合\(L\)とは
$$
L=\left\{c_1\boldsymbol{e}_1+c_2\boldsymbol{e}_2\middle|c_1,c_2\in\mathbb{Z}\right\}
$$
を指します。
さて、\(n=5\)の場合を考えてみます。
凸多角形を構成する格子点の任意の\(5\)点を\(\boldsymbol{x}_1,\boldsymbol{x}_2,\boldsymbol{x}_3,\boldsymbol{x}_4,\boldsymbol{x}_5\)と書くと、\(\boldsymbol{x}_i\ (i=1,\dots,5)\)は\(c_i,d_i\in\mathbb{Z}\ (i=1,\dots,5)\)を用いて
\begin{eqnarray}
\boldsymbol{x}_i=c_i\boldsymbol{e}_1+d_i\boldsymbol{e}_2
\end{eqnarray}
と書くことが出来ます。
要するに、格子点\(\boldsymbol{x}_i\)の座標が\((c_i,d_i)\)ということです。
このとき、ある\(2\)点\(\boldsymbol{x}_i\)、\(\boldsymbol{x}_j\ (i,j=1,\dots,5,\ i\neq j)\)が存在して、直線
$$
y=\frac{d_j-d_i}{c_j-c_i}x+d_i-\frac{d_j-d_i}{c_j-c_i}c_i
$$
が整数解を持つ、ということが今回の問題の主張で、これを証明しなさい、というわけです。
しかし、これは計算量も多くなることが予想されますので、この方法は使わないことにしました。
さあさあ、どうしようか、と思いましたが、修士のときの研究を思い出しました。
研究していたことがそのまま使えたわけではないのですが、目の付け方を思い出したわけです。
閃いた回答
整数が絡む問題を考えるとき、整数をグループ分けするとわかりやすいということがあります。
例えば、素数に着目して素因数分解を考えるというのが1つの手です。
他にもたくさん手法はあるでしょうが、筆者が思い出したのは「偶奇で分ける」ということです。
格子点の座標を偶奇で分類すると、
です。
つまり格子点の座標は偶奇に着目することで4つのグループに分けることが出来ます。
今、凸多角形を構成する格子点の個数は5つ以上なので、先程の4つのグループのうち、少なくとも1つのグループには必ず2つ以上の点が含まれていることになります(抽斗論法)。
- (偶,偶)に2つ以上の点が含まれる場合
偶\(-\)偶\(=\)偶ですので、\(x\)座標、\(y\)座標共に偶数です。
したがって、この2頂点を結ぶ編もしくは対角線の中点の座標は有理整数ですので、格子点です。 - (偶,奇)に2つ以上の点が含まれる場合
偶\(-\)偶\(=\)偶、奇\(-\)奇\(=\)偶ですので、この場合も\(x\)座標、\(y\)座標共に偶数です。
したがって、この2頂点を結ぶ編もしくは対角線の中点の座標は有理整数ですので、格子点です。 - (奇,偶)に2つ以上の点が含まれる場合
奇\(-\)奇\(=\)偶、偶\(-\)偶\(=\)偶、ですので、この場合も\(x\)座標、\(y\)座標共に偶数です。
したがって、この2頂点を結ぶ編もしくは対角線の中点の座標は有理整数ですので、格子点です。 - (奇,奇)に2つ以上の点が含まれる場合
奇\(-\)奇\(=\)偶ですので、\(x\)座標、\(y\)座標共に偶数です。
したがって、この2頂点を結ぶ編もしくは対角線の中点の座標は有理整数ですので、格子点です。
問題2.に取り掛かりましたが、ふと「これ、さっきの方針と全く同じようにできるんじゃないか?」と思いました。
というのも、極端にいえば、\(y\)軸を斜めに傾けて、左上から右下への第3の軸を無視すれば、同じように証明できると思ったからです。
先程の方針は別段直交座標系であることに依存してはいませんし、第3の軸の有無も関係ありません。
したがって、格子点の偶奇を分けるという方針で全く同じように証明できます。
投稿されたエレガントな回答
筆者と似ている回答がありましたので、それについては省略します。
2番について「1番と同じなのに、何か違いがあるのだろうか」とあったが、悩まれた方に弁明しておくと、「本質的にははまったく同じであるが、直線が3方向に並ぶことで、盲点になりうる」ということで、「同じなのだ」と気づくかどうかの問題として出題した。
(中略)
1.については出題者の解答と同じ(言い回しのち外はいろいろあるが)であるものが非常に多かった。しかし、出題者の解答のように、格子点を、元のままの座標で考える方法を頂点の一つを原点とした場合は、また2種類に分かれていた。一つは、他の頂点には(偶,偶)の座標を持つ点はない(あれば、その点と原点とを結ぶ編または対角線の中点が格子点だから)として話をすすめる。すると、他の頂点は(奇,奇)、(奇,偶)、(偶,奇)の3種類で、4点以上あるから、ということで、出題者の解答と同様な解答になっていた。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p119-p121.
2.については、出題者の解答のように、斜交座標系へ単純にもって言った解答は案外少なかった。基本単位ベクトルを考えることによって、実質的に斜交座標系を考えたことに成っているものが多数を占めた。残りの大部分は、線型写像によった説明であった。行列をい用いたものと、変換行列は明示しないで「線型写像」という言葉を用いていたものとがあった。しかし、この場合、線型写像を利用するより、単純に遮光座標系を考える方が良いと思う。
どうやら筆者の回答は出題者が用意していた解答とほぼ同じだったようです。
読者の皆様への挑戦状!
今から紹介する問題の解答は今週の木曜日に解説します!
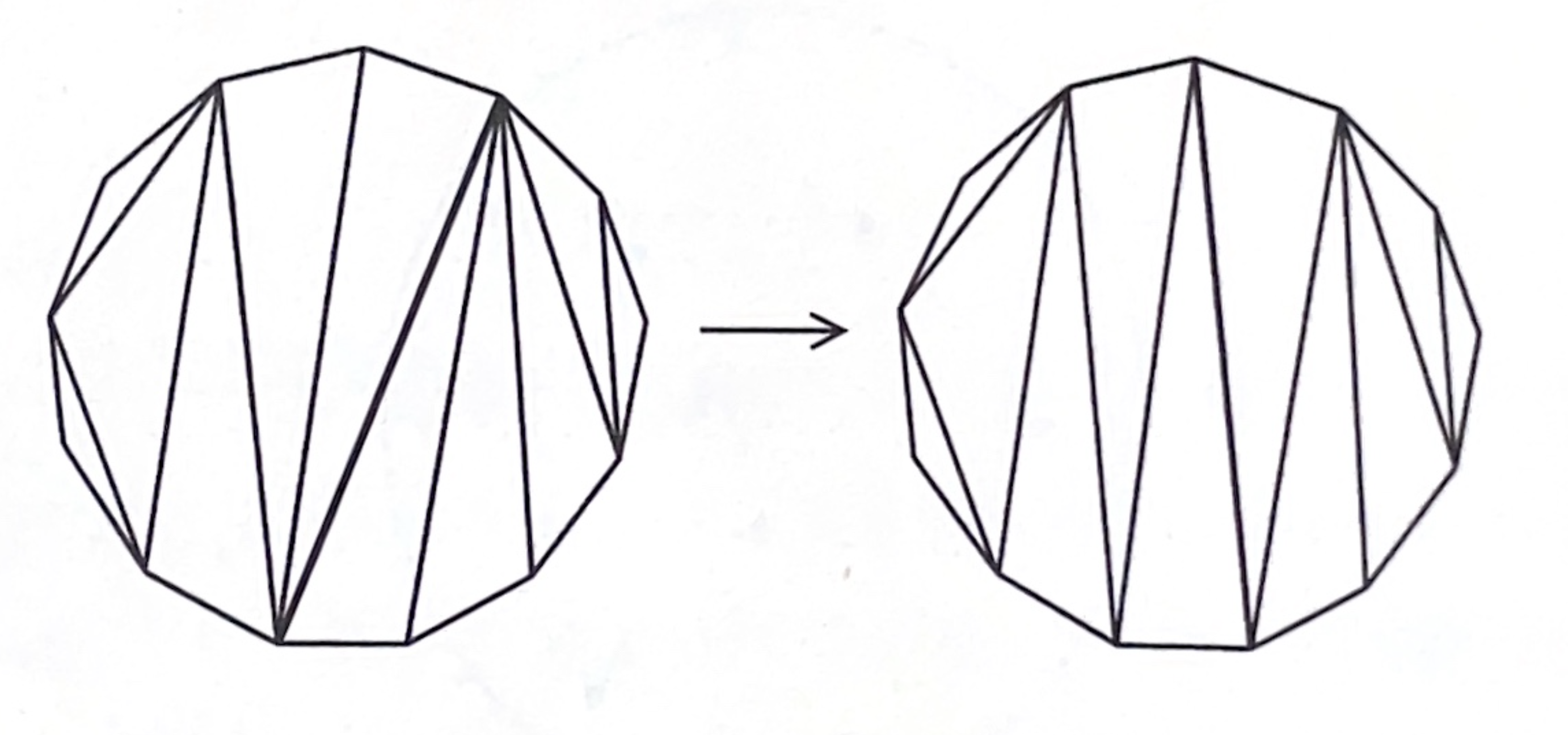
正十三角形に対角線を加えて三角形に分割した図形を考えます。下図のように、その1つの対角線に注目して、それを挟んでいる2つの三角形が作る四角形の中で対角線を切り替える操作を対角変形と呼ぶことにします。どのように対角線を入れた2つの正十三角形も対角変形を繰り返すことにり、お互いに移り合います。どんな場合でも何回以下で移り合うでしょうか?
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p17.
前回の問題は【1時間チャレンジシリーズ】挑戦⑮を御覧ください。
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする