本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください。
では、問題
\(\triangle ABC\)の\(\angle B\)、\(\angle C\)の2等分線が、それぞれ大変\(AC\)、\(AB\)と交わる点を\(D\)、\(E\)とするとき
$$
\angle ADE-\angle AED=60^\circ
$$
ならば、\(\angle ACB\)はどんな角でしょうか。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p14.
いざ、チャレンジ
チャレンジの結果…解けませんでした…
いやあ、今回は難しかったです。
言い訳になってしまいますが、補助線を引きまくれば出来るのでしょうが、そうなるとあまり良い解答とは思えず、頭を捏ねくり回しましたがだめでした。
解けなかったら元も子もないので、あまり良い発想ではないのでしょうけれど…
筆者の回答
解けなかったとはいえ、筆者がどのように考えたのか、ということを記します。
まず、角の二等分線を引いているので、「内心を使うのだな?」と思いました。
しかし、\(BD\)と\(CD\)との交点が内心だ、ということが分かったとて、そこから進みませんでした。
そこで、仮定
$$
\angle ADE-\angle AED=60^\circ\tag{1}
$$
のように、具体的な角度の数値は考えず、連立方程式的に解くことで求めたい角が得られるかな?とも思い、各角の関係式を考えてみることにしました。
※以下、結果的に意味のないことを書きます。
\(\triangle AED\)の内角の和は\(180^\circ\)なので、
$$
\angle A+\angle AED+\angle ADE=180^\circ\tag{2}
$$
が成り立ちます。
これと仮定(1)から
$$
\angle A+2\angle ADE=240^\circ\tag{3}
$$
が得られます。
また、\(\triangle ABC\)の内角の和も\(180^\circ\)であることと、\(\angle B=2\angle ABD\)、\(\angle C=2\angle ACE\)であることから
$$
\angle A+2\angle ABD+2\angle ACE=180^\circ\tag{4}
$$
が得られます。
(3)と(4)から
$$
2\angle ADE-2\angle ABD-2\angle ACE=60^\circ=\angle ADE-\angle AED
$$
が得られます。
…得られましたが、だからどうした、という話です。
この方針は一旦やめました。
次に、\(\angle A\)から線分\(BD\)と線分\(CE\)との交点\(F\)を結ぶ線分を作図すると、\(F\)は\(\triangle ABC\)の内心なので、線分\(AF\)は\(\angle A\)を二等分します。
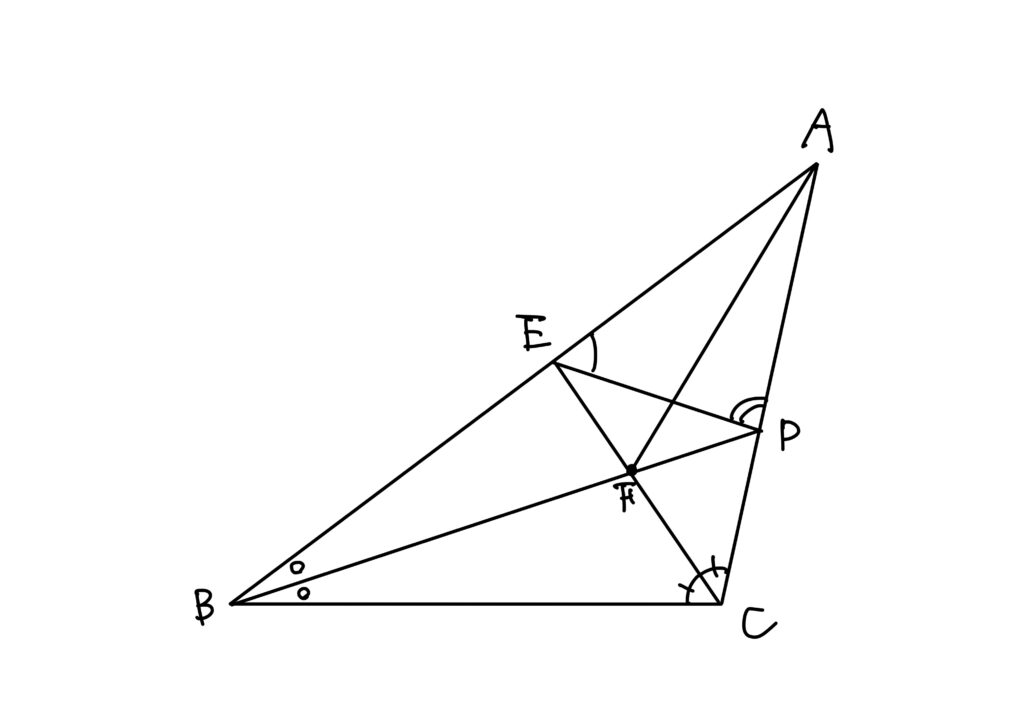
更に、\(F\)は内心だから、
\begin{eqnarray}
\angle BFC&=&2\triangle +\circ+\times\\
&=&\circ+\triangle +\times+\triangle \\
&=&90^\circ+\triangle \\
&=&\angle EFD
\end{eqnarray}
です。
最後の等式は対頂角により等しいことを指しています。
\(AF\)と\(ED\)の交点を\(G\)とします。
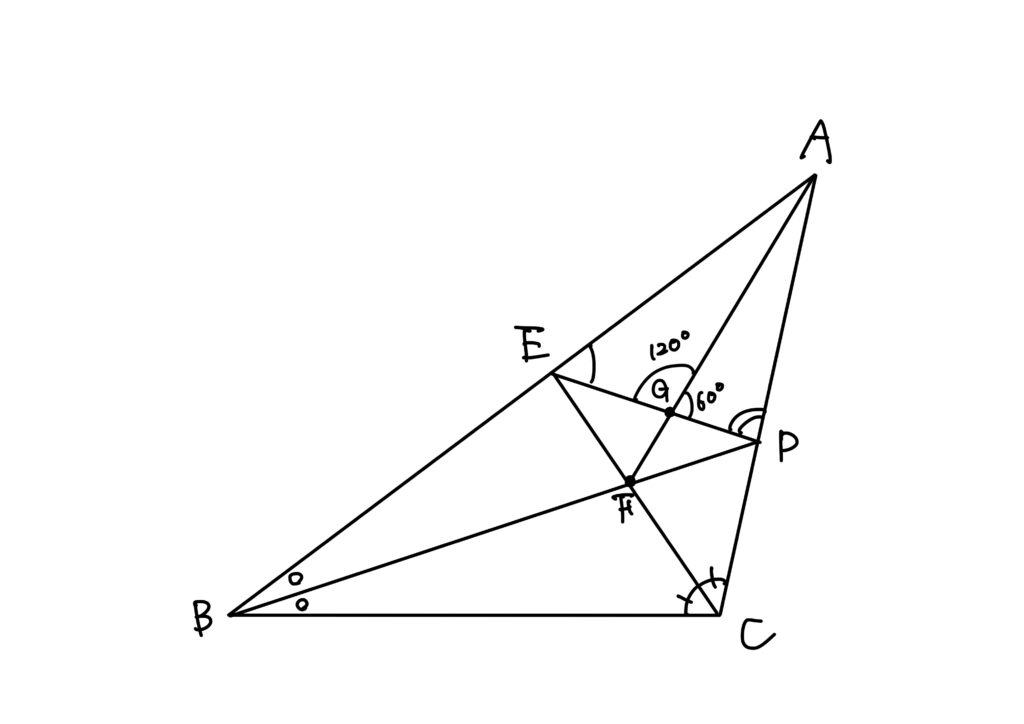
すると、
\begin{eqnarray}
\angle AGD&=&\angle EAG+\angle AEG=\triangle +\angle AED\\
\angle AGE&=&\angle DAG+\angle ADG=\triangle +\angle ADE\\
\end{eqnarray}
です。
この方程式の辺々の差を取ることで
\begin{eqnarray}
\begin{cases}
\angle AGE-\angle AGD=\angle ADE-\angle AED=60^\circ\\
\angle AGE+\angle AGD=180^\circ
\end{cases}
\end{eqnarray}
という連立方程式が得られます。
これを解けば、\(\angle AGE=120^\circ\)、\(\angle AGD=60^\circ\)が得られます。
…得られましたが、だからどうした、でした。
他にも数個方程式を立てましたが、どれも「だからどうした」でした。
ここでタイムアップでした…
投稿されたエレガントな回答
解1(中略)
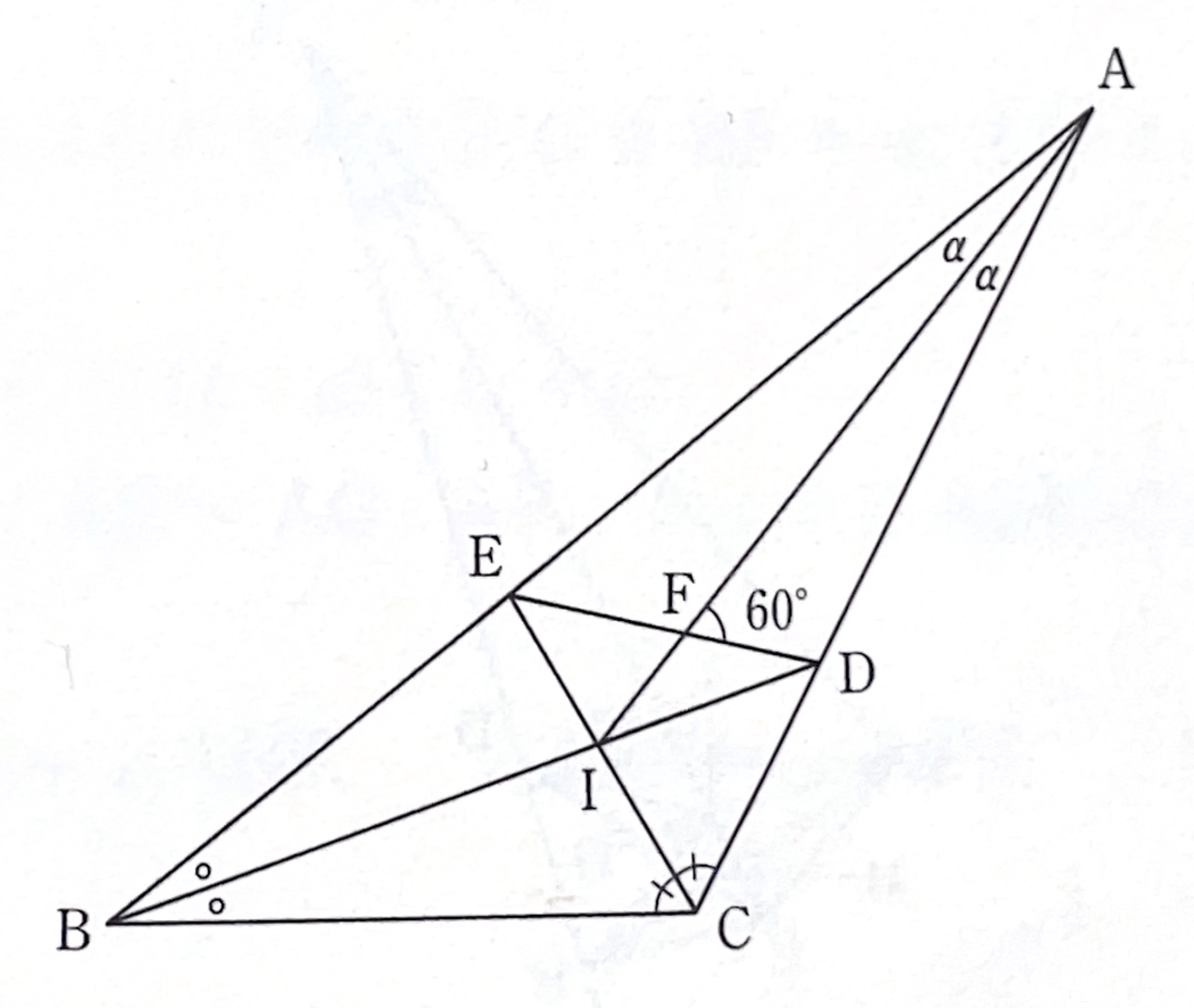
\(BD\)、\(CE\)の交点を\(I\)とすれば、\(I\)は内心であるから\(AI\)は\(\angle BAC\)を2等分する。
\(\angle BAI=\angle IAC=\alpha\)とおけば、内心の性質として\(\angle BIC=90^\circ+\alpha\)。よって
$$
\angle DIE=\angle BIC=90^\circ+\alpha\tag{1}
$$
\(AI\)と\(DE\)の交点を\(F\)とすれば
\begin{eqnarray}
\angle AFE-\angle AFD&=&\left( \alpha+\angle ADE\right)-\left( \alpha+\angle AED\right)\\
&=&\angle ADE-\angle AED=60^\circ.
\end{eqnarray}
\(\angle AFE+\angle AFD=180^\circ\)であるから
$$
\angle AFE=120^\circ,\quad \angle AFD=60^\circ
$$
である。
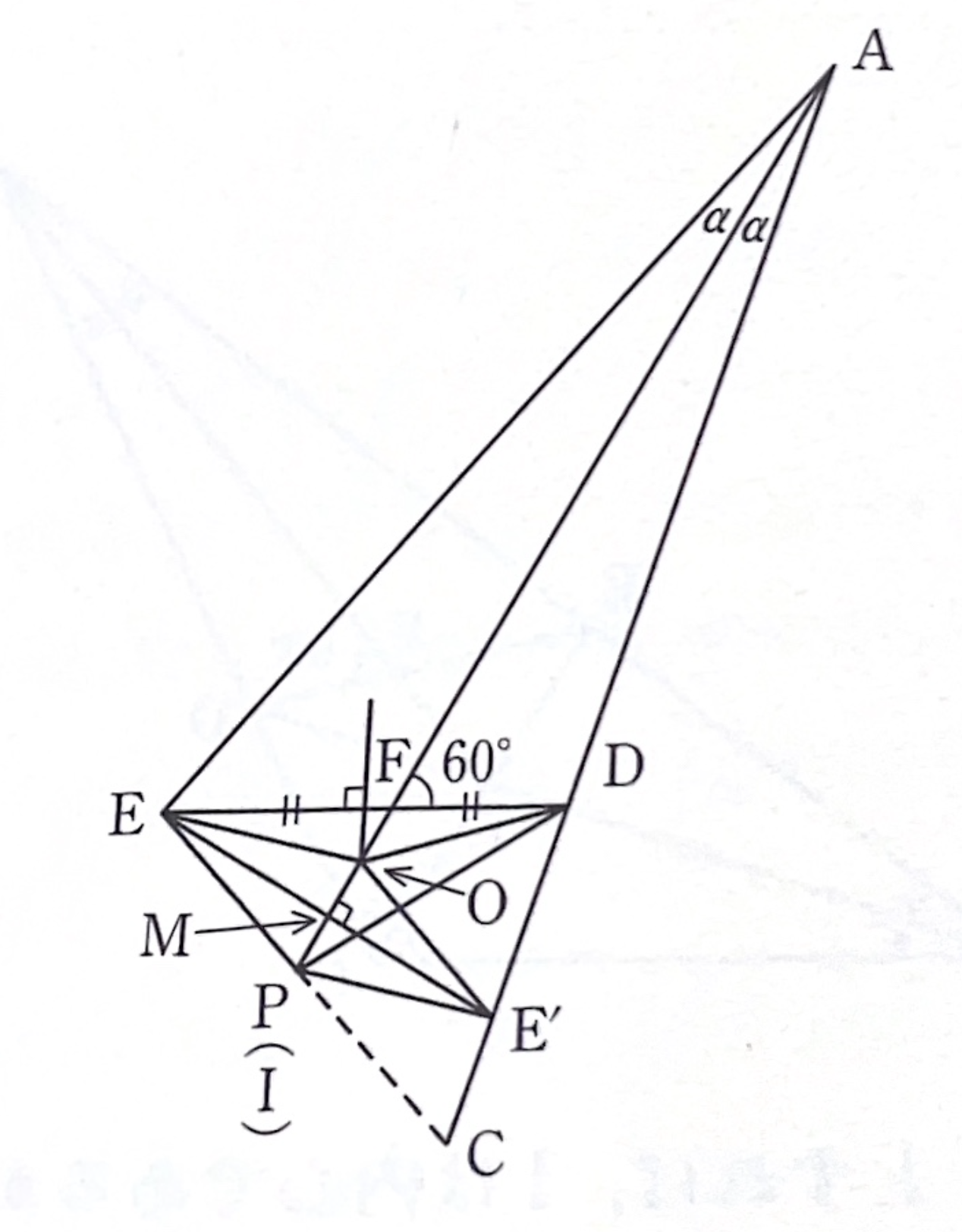
したがって、\(\angle EFI=\angle AFD=60^\circ\)である。\(DE\)の垂直二等分線と\(AF\)との交点を\(O\)とすると、\(OD=OE\)である。また\(E\)から\(AF\)への垂線の足を\(M\)とし、\(EM\)と\(AD\)との交点を\(E^\prime\)とすると\(\angle EAM=\angle E^\prime AM\)から\(EM=ME^\prime\)である。これより、\(OE=OE^\prime\)で\(O\)は\(\triangle DEE^\prime\)の外心である。
\(\angle EFM=60^\circ\)であるから\(\angle DEE^\prime=\angle FEM=30^\circ\)。したがって
$$
\angle DOE^\prime=2\angle DEE^\prime=60^\circ.
$$
これと\(OD=OE^\prime\)から\(\triangle ODE^\prime\)は正三角形である。
\(O\)の\(M\)に関する対象点を\(P\)とすると、\(M\)は\(OP\)、\(EE^\prime\)の共通な中点で\(OP\perp EE^\prime\)だから四辺形\(OEPE^\prime\)はひし形である。よって
\begin{eqnarray}
\angle EPO&=&\angle POE^\prime=\angle PE^\prime A+\angle OAE^\prime\\
&=&\angle OE^\prime D+\alpha=60^\circ+\alpha.
\end{eqnarray}
また\(E^\prime P=E^\prime O=E^\prime D\)から\(E^\prime\)は\(\triangle OPD\)の外心である。よって
$$
\angle DPO=\frac{1}{2}\angle DE^\prime O=30^\circ.
$$
ゆえに
$$
\angle DPE=\angle DPO+\angle EPO=30^\circ+60^\circ+\alpha=90^\circ+\alpha
$$
よって(1)から\(\angle DPE=\angle DIE\)。
\(P\)、\(I\)は\(\angle A\)の2等分線上の点で、どちらも\(DE\)に関して\(A\)と反対側にあるから、\(P\)、\(I\)は一致する。すなわち\(P\)は\(\triangle ABC\)の内心である。よって\(EP\)は\(C\)を通る。\(OE^\prime /\!/ EP\)だから\(OE^\prime /\!/ EC\)。したがって\(\angle ACE=\angle DE^\prime O=60^\circ\)。よって
$$
\angle ACB=2\angle ACE=120^\circ
$$
である。解2(中略)
\(BC=a\)、\(CA=b\)、\(AB=c\)とおく。\(BD\)は\(\angle B\)の2等分線であるから
$$
AD:DC=AB=c:a.
$$
よって
$$
AD:AC=c:(c+a),\quad \therefore\ AD=\frac{bc}{c+a}
$$
同様に\(\displaystyle AE=\frac{bc}{b+a}\)であるから
$$
AD:AE=\frac{1}{c+a}:\frac{1}{b+a}=(b+a):(c+a).
$$
\(AB\)、\(AC\)の延長上にそれぞれ点\(F\)、\(G\)を\(BF=a\)、\(CG=a\)となるようにとれば
$$
AG:AF=(b+a):(c+a)
$$
であるから\(AD:AE=AG:AF\)、よって\(\triangle ADE\text{∽}\triangle AGF\)である。
したがって
$$
\angle ADE=\angle AGF,\quad \angle AED=\angle AFG.
$$
よって
$$
\angle AGF-\angle AFG=\angle ADE-\angle AED=60^\circ.
$$
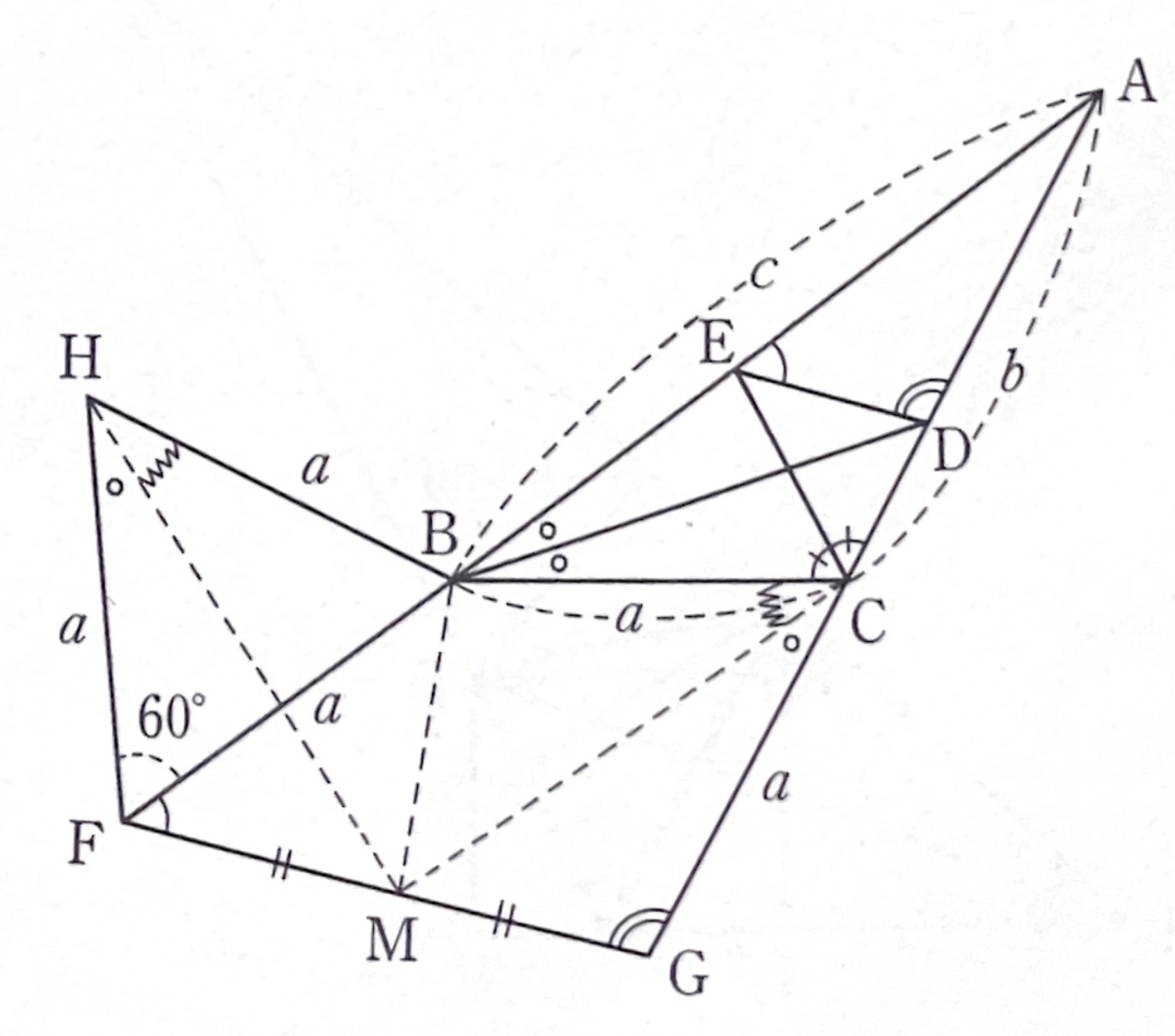
正三角形\(BFH\)を\(\triangle AFG\)の外側に作り、\(FG\)の中点を\(M\)とすると、
\begin{eqnarray}
&&FH=FB=a=GC,\quad FM=GM,\\
\angle MFH=\angle AFG+60^\circ=\angle AGF=\angle MGC
\end{eqnarray}
より\(\triangle MFH\equiv \triangle MGC\)である。
よって
$$
\angle MHF=\angle MCG,\quad MH=MC.
$$
また\(BH=BF=BC\)で\(BM\)は共通であるから
$$
\triangle MBH\equiv \triangle MBC,\quad よって\quad \angle MHB=\angle MCB.
$$
したがって
\begin{eqnarray}
\angle BCG&=&\angle MCB+\angle MCG=\angle MHB+\angle MHF\\
&=&\angle BHF=60^\circ,
\end{eqnarray}
ゆえに\(\angle ACB=180^\circ-\angle BCG=120^\circ\)である。
(\(\angle BCG=\angle BHF\)は、四辺形\(CHGF\)が等脚台形であることを用いて証明することもできる。また\(\angle BCG=60^\circ\)は背理法を用いても証明できる。)解3(中略)
\(\angle AED=\theta\)とおけば\(\angle ADE=\theta+60^\circ\)である。また\(\angle ADE>\angle AED\)だから\(AE>AD\)である。\(D\)から\(AB\)、\(BC\)への垂線の足を\(F\)、
\(H\)とすれば\(BD\)は\(\angle B\)を2等分するから\(DF=DH\)である。同様に\(E\)から\(AC\)、\(BC\)への垂線の足を\(G\)、\(I\)とすれば\(EG=EI\)である。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p91-p95.
\(\triangle ADF∽\triangle AED\)であるから
$$
\frac{DF}{EG}=\frac{AD}{AE}<1,\quad よって\quad DF<EG.
$$
したがって、\(DH<EI\)である。\(D\)から\(EI\)への垂線の足を\(K\)とすれば\(KI=DH<EI\)より、\(K\)は線分\(EI\)上の点である。
\begin{eqnarray}
DE\cos\left( \angle DEC\right)&=&EK=EI-DH=EG-DF\\
&=&DE\sin \left( \angle EDG\right)-DE\sin\left( \angle DEF\right)\\
&=&DE\sin\left( \angle EDA\right)-\sin\left( \angle DEA\right)\\
&=&DE\sin\left( \theta+60^\circ\right)-DE\sin \theta\\
&=&DE\left\{\sin(\theta+60^\circ)\sin\theta\right\}\\
&=&DE\cdot 2\sin30^\circ\cos\left( \theta+30^\circ\right)\\
&=&DE\cos\left(\theta+30^\circ \right)
\end{eqnarray}
よって
$$
\cos\left( \angle DEK\right)=\cos\left( \theta+30^\circ\right)
$$
ゆえに\(\angle DEK=\theta+30^\circ\)。
また\(\angle DEG=\left( \theta+60^\circ\right)-90^\circ=\theta-30^\circ\)。よって
$$
\angle GEK=\angle DEK-\angle DEG=\left( \theta+30^\circ\right)-\left( \theta-30^\circ\right)=60^\circ.
$$
すなわち\(\angle GEI=60^\circ\)。
四辺形\(EICG\)において\(\angle I=\angle G=90^\circ\)だから\(\angle IEG+\angle ICG=180^\circ\)、よって\(\angle ICG=180^\circ-60^\circ=120^\circ\)。
ゆえに\(\angle ACB=120^\circ\)である。
いやあ、すごいですね。
発想が豊かです。
しかし、エレガントか、というとどうなんでしょう。
結構力技の解答な気がしました。
解けてないくせに何を言ってるんだ、という話ですがね。
読者の皆様への挑戦状!
今から紹介する問題の解答は今週の土曜日に解説します!
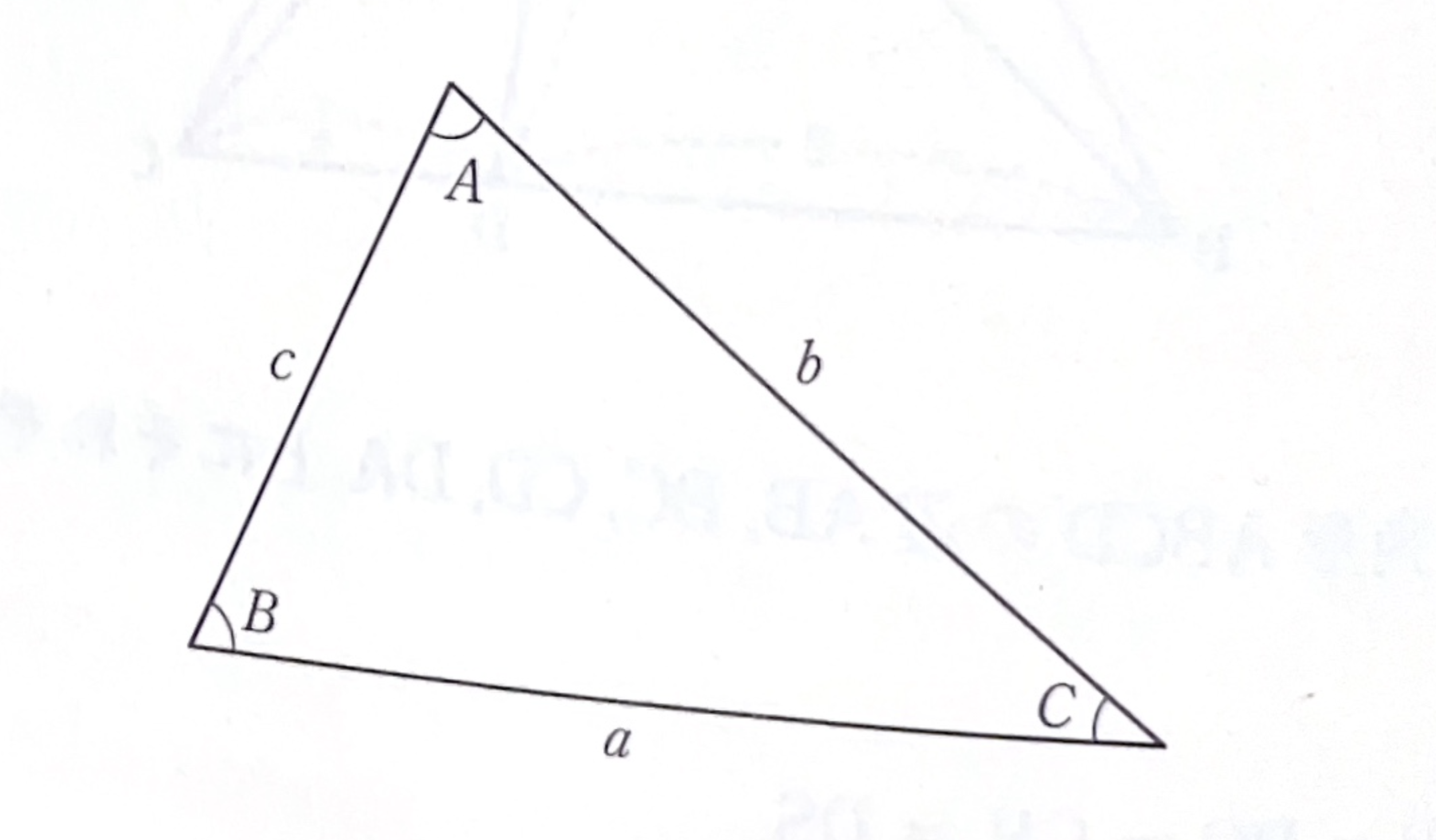
3辺が整数\(a,b,c\)の3角形の3つの角\(A,B,C\)が特別の1次の関係式をもつ場合があります。
もちろん
$$
A+B+C=180^\circ
$$
は当然成立しますが、それと無関係の(線型独立な)関係式で係数が整数のものを見つけて下さい。たとえば図1、図2についてはそのような1次式があります。まずこれみつけてください。
それから、このような1次式をもつ整数の辺の3角形が(相似形をのぞき)他にもあるか、無限にあるか、どのような1次式のものであるか、などについても研究してみてください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p14-p15.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております







コメントをする