本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
問題を明示します。
\(xyz-\)空間内の同一平面上にない\(4\)点\({\rm P_1},\cdots,{\rm P_4}\)が与えられたとき、この\(4\)点をとおる曲線の方程式をひとつ与えて下さい。また、その方程式を使って、\({\rm P_1}=(1,0,0),\ {\rm P_2}=(0,1,0),\ {\rm P_3}=(0,0,1),\ {\rm P_4}=(0,0,0)\)の場合にその曲線のグラフを描いてください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p25.
もちろん、そのような曲線は無数にありますが、できるだけ方程式が美的なもの、簡単なもの、あるいはおもしろいものを捜してください。また、曲線は閉曲線(楕円のように輪になって閉じたもの)でも開曲線(放物線のように無限遠まで伸びていくもの)でもよく、4点は順に並んでいなくてもよいことにします。ただし双曲線2つの曲線に分解できるような曲線(可約曲線)は、好ましくありません。
チャレンジの結果…?
チャレンジの結果…解けませんでした…
1時間では時間が足りず、「もっと効率的な方法があったんじゃないかな」と反省しています。
一応、「それっぽいもの」は出たのですが、果たして本当に題意に合致するかの確認ができませんでした。
筆者の解答を紹介します。
まず、どういう手法で曲線を見つけるのか?という話なのですが、筆者の中でパッと思いついたのは
- 手書きの曲線を描いて、その曲線の方程式を推定
- 媒介変数表示
の2つです。
問題には「簡単なもの」という条件が含まれているので、筆者はそこに着目することにしました。
とはいえ、何か基となる曲線がほしいところです。
もしそれがあれば、後は平行移動やら拡大縮小やらで話が終わります。
そこで思いついたのはリサージュ図形です。
リサージュ図形ってどんなの?(解答とは関係ないので読み飛ばしてOKです)
2次元の場合のリサージュ図形は
\begin{eqnarray}
\begin{cases}
x(\theta)=a\cos\left( \omega \theta+\delta\right)\\
y(\theta)=b\sin \theta
\end{cases}
\end{eqnarray}
と媒介変数で表される曲線です。
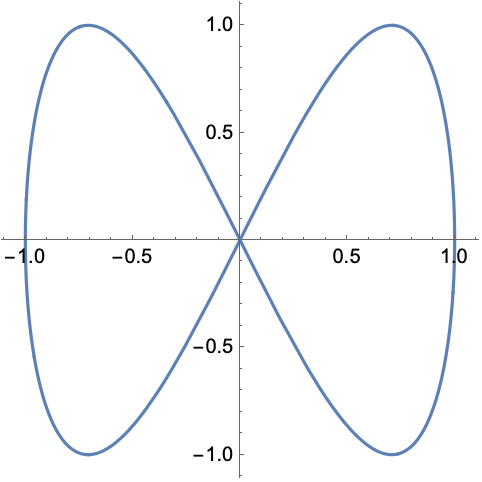
例えば、
\begin{eqnarray}
\begin{cases}
x(\theta)=\sin\theta\\
y(\theta)=\sin 2\theta
\end{cases}
\end{eqnarray}
は以下のような曲線です。
3次元の場合は
\begin{eqnarray}
\begin{cases}
x(\theta)=a\cos\left( \omega_x \theta+\delta_x\right)\\
y(\theta)=b\sin\left( \omega_y \theta+\delta_y\right)\\
z(\theta)=c\cos\left( \omega_z \theta+\delta_z\right)\\
\end{cases}
\end{eqnarray}
のような媒介変数で表される曲線です。
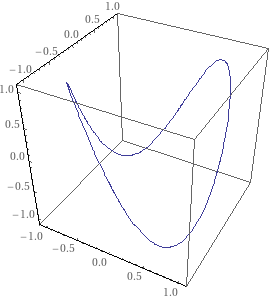
例えば、
\begin{eqnarray}
\begin{cases}
x(\theta)=\cos\theta\\
y(\theta)=\sin\theta\\
z(\theta)=\sin2\theta
\end{cases}
\end{eqnarray}
は以下のような曲線です。
筆者の解答を結論だけ
極端な話、先程挙げた
\begin{eqnarray}
\begin{cases}
x(\theta)=\cos\theta\\
y(\theta)=\sin\theta\\
z(\theta)=\sin2\theta
\end{cases}
\end{eqnarray}
をうまく帳尻合わせしたものが筆者の解答です。
解答としては
\begin{eqnarray}
\begin{cases}
x(\theta)=\frac{1}{4}\left(1+2\cos\frac{\pi\theta}{2}+\cos\pi\theta \right)\\
y(\theta)=\frac{1}{4}\left(1-\cos\pi\theta\right)\\
z(\theta)=\frac{1}{4}\left(1-2\cos\frac{\pi\theta}{2}+\cos\pi\theta \right)\\
\end{cases}
\end{eqnarray}
です。
※間違っています。
結構複雑ですが….
解答に至った経緯(さらっと)
スタートは
\begin{eqnarray}
\begin{cases}
x(\theta)=\cos\theta\\
y(\theta)=\sin\theta\\
z(\theta)=\sin2\theta
\end{cases}
\end{eqnarray}
でした。
勿論、\(\cos\theta=\sin\theta=0\)を満たすような\(\theta\)はありませんので、このままではダメです。
そこで
\begin{eqnarray}
\begin{cases}
x(\theta)=\cos\left( \theta+\frac{\pi}{2}\right)\\
y(\theta)=\sin\theta\\
z(\theta)=\sin2\theta
\end{cases}
\end{eqnarray}
としてみました。
これも\((0,0,1)\)を通らないため、ダメです。
次に、
\begin{eqnarray}
\begin{cases}
x(\theta)=\cos\left( \theta+\frac{\pi}{2}\right)\\
y(\theta)=\sin\theta+1\\
z(\theta)=-\sin\theta-1
\end{cases}
\end{eqnarray}
もやってみましたが、後から考えると、\(y(\theta)=-z(\theta)\)を満たすため、\((0,1,0)\)を通りません。
ここまででもう30分ほど経ってしまいました。
そして「これはちょっと変えただけでは無理だな…」と思い、「\(\cos\)だの\(\sin\)だのを追加しなければならんな」と思いました。
それからはココに書ききれないほど「あーでもない、こーでもない」を繰り返していました。
そして
\begin{eqnarray}
\begin{cases}
x(\theta)=\frac{1}{4}\left(1+2\cos\frac{\pi\theta}{2}+\cos\pi\theta \right)\\
y(\theta)=\frac{1}{4}\left(1-\cos\pi\theta\right)\\
z(\theta)=\frac{1}{4}\left(1-2\cos\frac{\pi\theta}{2}+\cos\pi\theta \right)\\
\end{cases}
\end{eqnarray}
はどうかな?ということろで時間切れでした。
今思えば、「回転行列やらを使って係数などに対する連律方程式を解けばもっと早く正確にできたんじゃないか…?」などと少々反省しています。
投稿されたエレガントな解答
(前略)
与えられた\(n\)点\({\rm P_1}=(x_1,y_1,z_1),\cdots,{\rm P_n}=(x_n,y_n,z_n)\)を通る曲線の方程式\(x=f(t),\ y=g(t),\ z=h(t)\)を考えましょう。それには、相異なる\(n\)個の点\(t_1,\cdots,t_n\)で与えられた値\(x_1,\cdots,x_n\)を持つような関数\(x=f(t)\)を作ればよいわけです。その方法の一つとして、
\((\ast)\)\(\qquad I_i(t_i)=1\)かつ、\(j\neq i\)のとき\(I_i(t_j)=0\)となるような関数\(I_i(t)\)を見つけて、\(f(t)=x_1I_1(t)+\cdots+x_nI_n(t)\)と表す方法が考えられます。特に、
\begin{eqnarray}
P_i(t)&=&\prod_{j\neq i}(t-t_j)\\
&=&(t-t_i)\cdots(t-t_{i-1})(t-t_{i+1})\cdots(t-t_n)
\end{eqnarray}
とし、\(I_i(t)=P_i(t)/{P_i(t_i)}\)とすれば、\((\ast)\)を満たす\(n-1\)次式\(I_i(t)\)が得られます。これをラグランジュの補間法と言います。\(t_i\)の選び方で\(I_i(t)\)はいろいろ変わりますが、例えば、\(n=4\)、\(t_i=i-1\ (1\leq i\leq 4)\)とすると、
$$
\begin{cases}
\displaystyle I_1(t)=\frac{-(t-1)(t-2)(t-3)}{6}\\
\displaystyle I_2(t)=\frac{t(t-2)(t-3)}{2}\\
\displaystyle I_3(t)=\frac{-t(t-1)(t-3)}{2}\\
\displaystyle I_4(t)=\frac{t(t-1)(t-2)}{6}
\end{cases}
$$
が得られ、この\(I_i(t)\)を用いて、
$$
\begin{cases}
x=x_1I_1(t)+\cdots+x_4I_4(t)\\
y=y_1I_1(t)+\cdots+y_4I_4(t)\\
z=z_1I_1(t)+\cdots+z_4I_4(t)\\
\end{cases}
$$
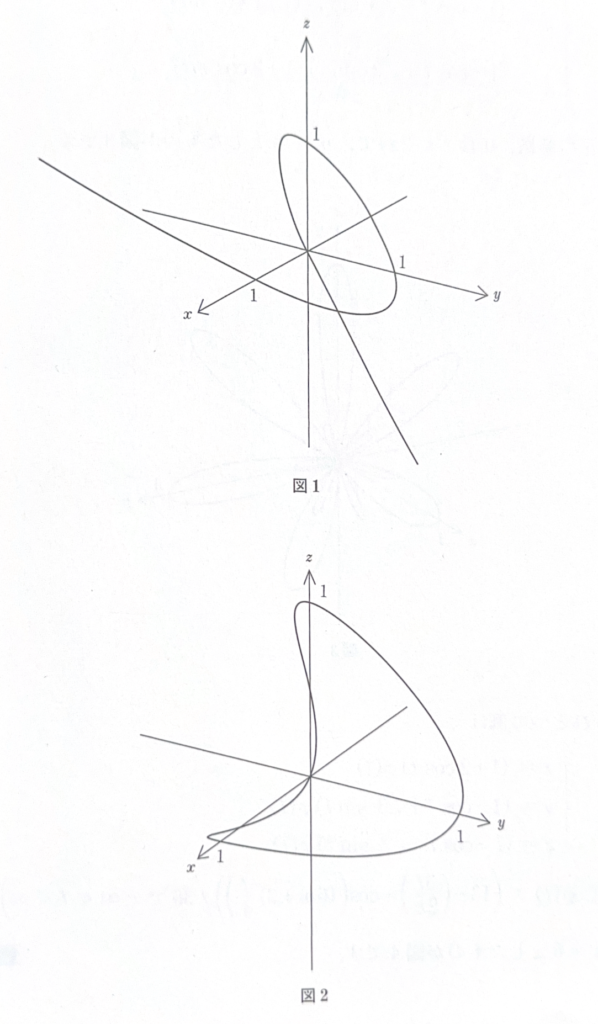
(\(-\infty<t<\infty\))とすれば、これが4点\({\rm P}_1,\cdots,{\rm P}_4\)を通る曲線の方程式になります。\({\rm P}_1=(1,0,0),\cdots,{\rm P}_4=(0,0,0)\)の場合のグラフは図1のとおりで、これは非特異3字有理曲線です。上の例は開局線でしたが、\(I_i(t)\)を三角関数を用いて構成することにより閉曲線を作ることもできます。基底の選び方でいろいろな例が作れますが、たとえば、\(1\)、\(\cos(\pi t/2)\)、\(\cos\pi t\)、\(\sin\pi t/2\)の一次結合を考え、
\begin{eqnarray}
\begin{cases}
I_1(t)=\frac{1+2\cos(\pi t/2)+\cos\pi t}{4}\\
I_2(t)=\frac{1-\cos\pi t+2\sin(\pi t/2)}{4}
I_3(t)=\frac{1-2\cos(\pi t/2)+\cos\pi t}{4}\\
I_4(t)=\frac{1-\cos\pi t-2\sin(\pi t/2)}{4}
\end{cases}
\end{eqnarray}
(\(0\leq t<2\pi\))とおけば、\(I_i(i-1)=1\)かつ、\(j\neq i-1\)である\(0\)以上\(3\)以下の整数\(j\)にたいし\(I_i(j)=0\)となるので上と同様に\(4\)点\({\rm P}_1,\cdots,{\rm P}_4\)を通る曲線の方程式が得られます。(中略)
$$
\begin{cases}
x=\frac{(1+2\cos t)(1+2\cos mt)}{9}\\
y=\frac{(1-\cos t+\sqrt{3}\sin t)(1+2\cos mt)}{9}\\
z=\frac{(1-\cos t+\sqrt{3}\sin t)(1+2\cos mt)}{9}
\end{cases}
$$
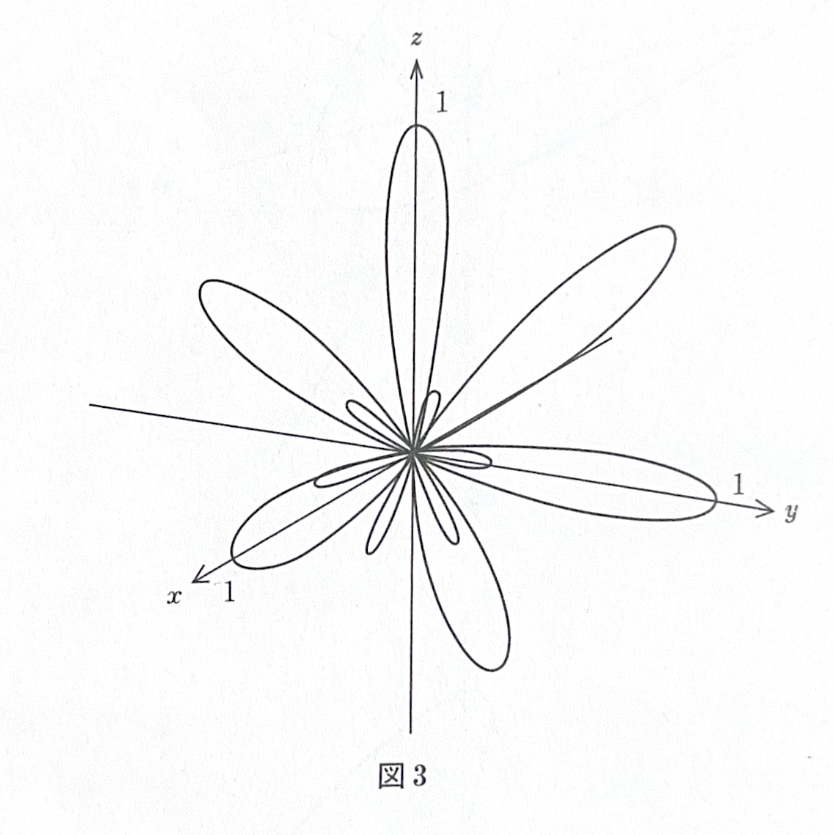
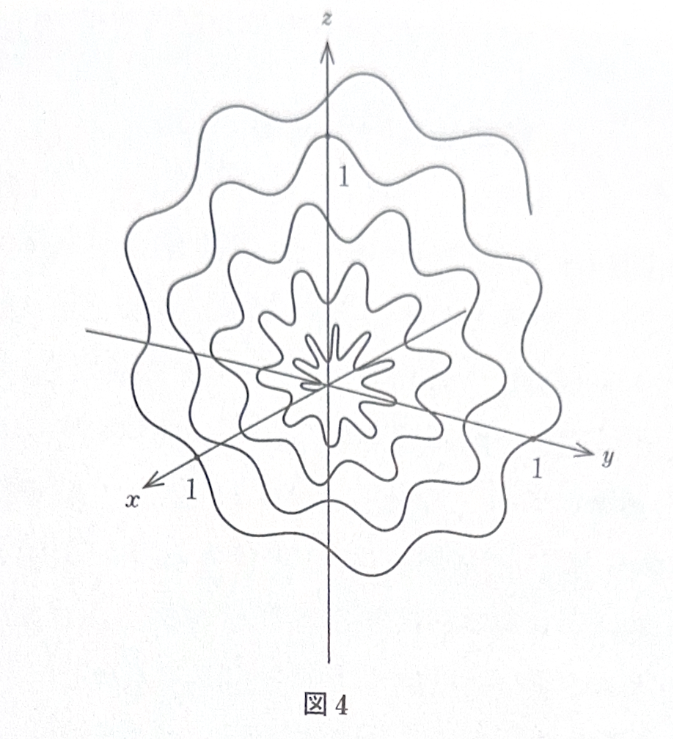
(\(m\)は整数、\(0\leq t2\pi\))で、\(m=6\)をとしたものが図3です。もうひとつの例は
$$
\begin{cases}
x=(1+2\cos t)\varphi(t)
y=(1-\cos t+\sqrt{3}\sin t)\varphi(t)\\
z=(1-cos t-\sqrt{3}\sin t)\varphi(t)
\end{cases}
$$
\(\Bigg(\)ただし、\(\displaystyle\varphi(t)=\left( 13-\left( \frac{3t}{2\pi}\right)-\cos\left( (6m+3)\frac{t}{4}\right)\right)\Big/36\)で\(-\infty<t<\infty\Bigg)\)で、\(m=6\)としたものが図4です。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p219-p223.
読者の皆様への挑戦状!
来週の日曜日に挑戦します!
平面上に\(n\)角形(凸とは限らない)の形をした図形がある。この図形を刑務所の平面図と見なすことにしよう。平面上の適切な位置に何台かの監視用カメラを設置し、刑務所の内部と外部の両方を監視したい。ただし、カメラが監視できる範囲を次のように定めます:
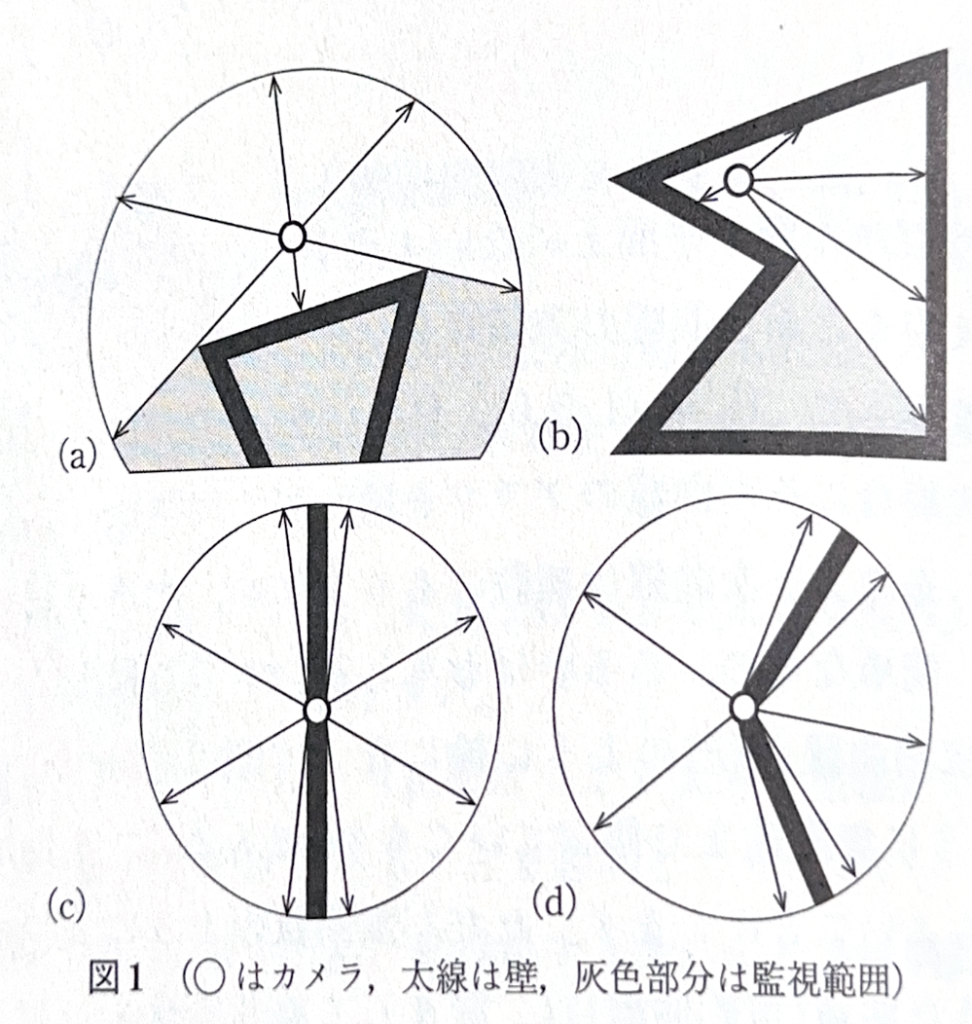
(1) さえぎる壁がない限り、カメラの視線は、その位置を中心として\(360^\circ\)の範囲を監視できる(図1(a),(b)参照)。
(2) 壁に設置されたカメラは壁の両側とも(内側も外側も)監視できる(図1(c),(d)参照)。
さて、刑務所の形がどんな形をした\(n\)角形であろうとも、平面全体を監視するために、高々\(\displaystyle \left\lfloor\frac{n+2}{2}\right\rfloor\)\(\Bigg(\)\(\displaystyle\frac{n+2}{2}\)の切り下げ\(\Bigg)\)台のカメラを適切な位置に設置すれば十分であることを証明して下さい。ただし、この問題は全て平面の問題としてと考えることにします。
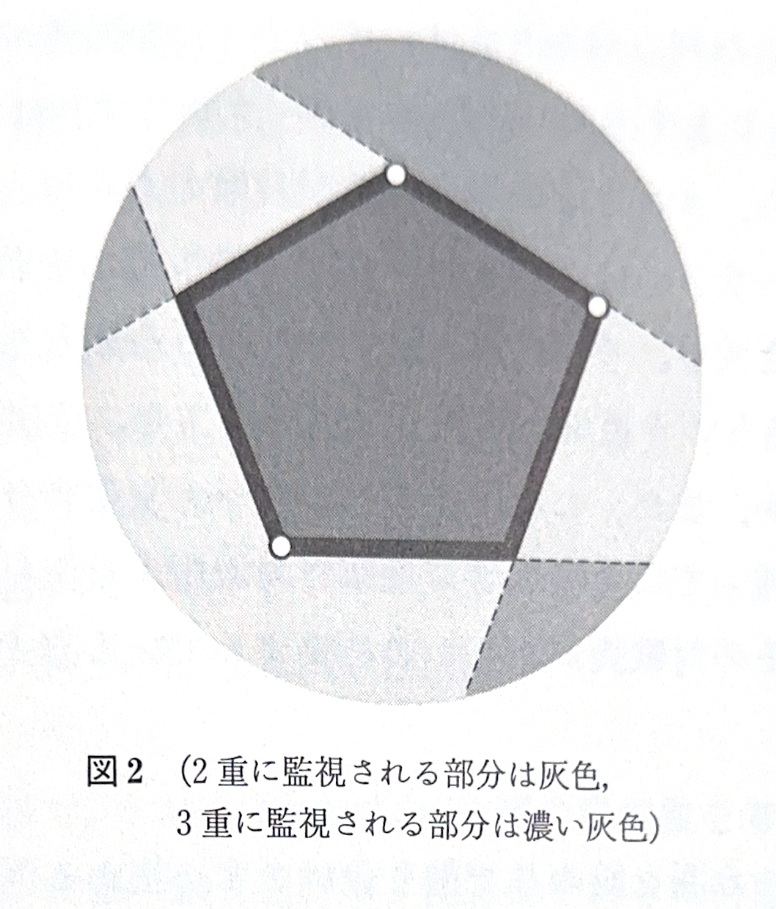
たとえば、図2のように、5角形の形をした刑務所ならば3台以上のカメラが必要です。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p25.
前回の問題は【1時間チャレンジシリーズ】挑戦㉝を御覧ください!
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ一週間ほどでお答えします。
(難しかったらもう少しかかるかもしれませんが…)
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!




コメントをする