本記事の内容
本記事は強連結成分について解説する記事です。
本記事を読むにあたり、有向グラフと強連結について知っている必要があるため、以下の記事も合わせてご覧ください。
前回、今回、次回で言いたいこと
前回、今回、次回で言いたいことは次の2つです。
定理0-1.
与えられた\(n\)次の正方行列\(A=\left( a_{ij}\right)\)が可約であれば、添字の番号を並べ替えることにより、次の行列に変形することが出来る。 $$ \begin{pmatrix} A_1&\ast&\ast&\cdots&\ast\\ O&A_2&\ast&\cdots&\ast\\ \vdots&\ddots&\ddots&\ddots&\ast\\ O&\cdots&O&A_{s-1}&\ast\\ O&O&\cdots&O&A_s\\ \end{pmatrix} $$ ただし、\(A_i\)は既約な正方行列である。これは次回証明します。
定理0-2.
有向グラフが強連結であることと、有向グラフの隣接行列が既約であることは同値である。この主張の十分性は前回証明しました。
必要性は次回証明します。
今回は、これらを示すために強連結成分について解説します。
(※ある種、次回の準備です。)
強連結成分を一言で。
強連結成分を一言で述べれば、
です。
実は、強連結成分とは何か?ということも大事ですが、それよりも
という事実が重要です。
ただし、この事実は「強連結でないグラフから強連結なグラフが作れる」と言っているわけではありません。
その前に、部分グラフ
と、説明する前に部分グラフについて解説します。
これは読んで字の如し、グラフの一部分のグラフ、という意味です。
これを数学的に書くと次です。
部分グラフ
グラフ\(X=(V,E)\)に対して、\(V_1\subset V\)、\(E_1\subset E\)とする。このとき、\(i(E_1)\subset V_1\times V_1\)かつ\(\overline{E_1}=E_1\)であるとき、\(X_1=\left( V_1,E_1\right)\)はグラフである。このグラフ\(X_1\)を\(X\)の部分グラフといい、\(X_1\subset X\)と書く。\(i(E_1)\subset V_1\times V_1\)のミソはグラフ\(X\)において存在する\(i\)と同じ\(i\)に対して、\(E_1\subset E\)の\(i\)による順像が\(V_1\times V_1\)の部分集合であるということです。
つまり、頂点\(V_1\)繋がり方が、元々のグラフ\(X\)との頂点\(V\)と同じ繋がり方をしていることを指しています。
\(\overline{E_1}\)は無向グラフなので、この条件が必要です。
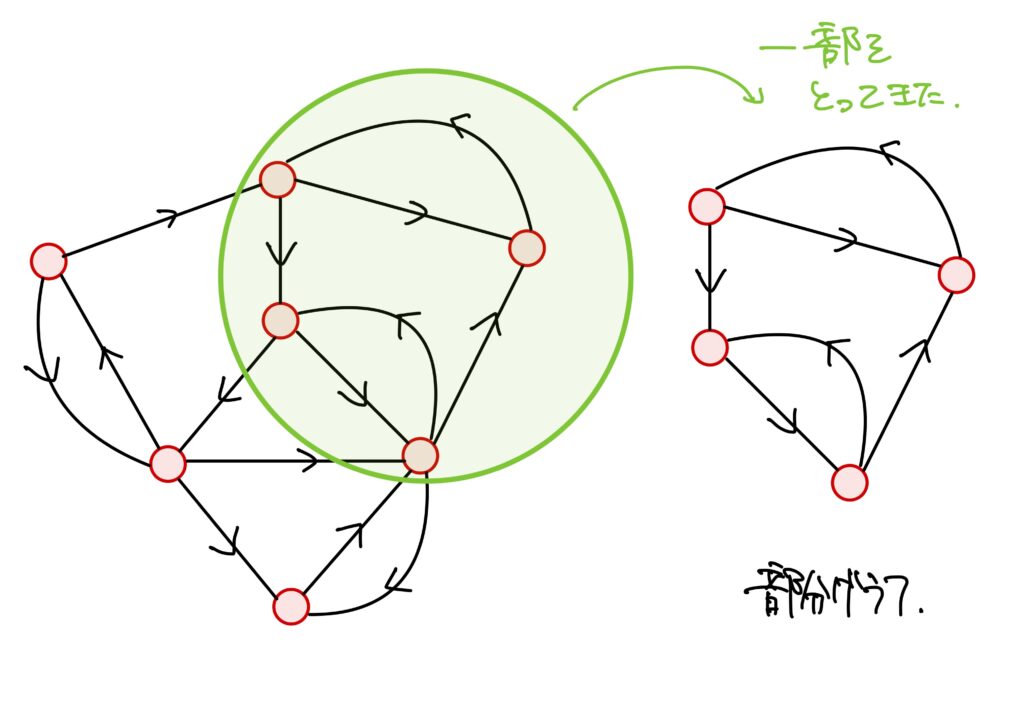
有向グラフの頂点の集合に「関係」を定めます。
先程「分解できる」という表現をしました。
「分解できる」は少し別の表現をすると「グループ分けすることができる」です。
ここで、「あ!あれだ!あれを使うんだ!」となってくださると嬉しいです。
答えは同値関係です。
同値関係の軽い復習
軽く同値関係を復習します。
同値関係
次の3条件を満たす集合\(X\)上の関係\(\sim\)を同値関係(equivalence relation)という。- \(x\in X\)のとき、\(x\sim x\)(反射律),
- \(x,y\in X\)のとき、\(x\sim y\Rightarrow y\sim x\)(対称律),
- \(x,y,z\in X\)のとき、\(x\sim y,\ y\sim z\Rightarrow x\sim z\)(推移律)
詳しくは、【論理と集合シリーズ】その7を御覧ください。
例えば、我々がよく使う\(=\)は同値関係です。
しかし、\(<\)やら\(>\)やら\(\geq\)やら\(\leq\)やらは同値関係ではありません。
同値関係の重要な性質の1つとして次があります。
定理1.
\(x\in X\)と同値な要素全体を\(C_x\)と書き、これを\(x\)の同値類(equivalence class)という。すなわち、 $$C_x=\{y\in X\mid x\sim y\}$$ である。 このとき、次が成り立つ。- \(x\in C_x\),
- \(C_x\cap C_y\neq \emptyset \Rightarrow C_x=C_y\),
- \(C_x\neq C_y\Rightarrow C_x\cap C_y= \emptyset\),
- \(\displaystyle\bigcup_{x\in X}C_x=X\),
- \(x,y\in X,\ x\neq y,\ \Rightarrow\ C_x\cap C_y=\emptyset\)

定理1.の証明は【論理と集合シリーズ】その7を御覧ください。
有向グラフの頂点の集合に同値関係を定めます。
「同値関係を定めます。」というのはあまり良い表現ではないかもしれません。
厳密には「有向グラフの頂点の集合に”うまく”関係を定めると、同値関係になる。」と表現すべきかもしれません。
さて、有向グラフの頂点の集合を\(\left\{1,\dots,n\right\}\)として、頂点の集合に次のような関係\(\sim\)を定めます。
頂点の集合における関係
与えられた有向グラフの頂点の集合を\(V=\left\{1,\dots,n\right\}\)とし、任意の頂点\(i,j\in V\)に対して次の関係を定める。つまり、\(i\)から辺をたどって\(j\)にたどり着く路と、\(j\)から辺をたどって\(i\)たどり着く路の双方が存在するときに「頂点\(i\)と頂点\(j\)には”関係がある”と言い、このときを\(i\sim j\)で表す。」というわけです。
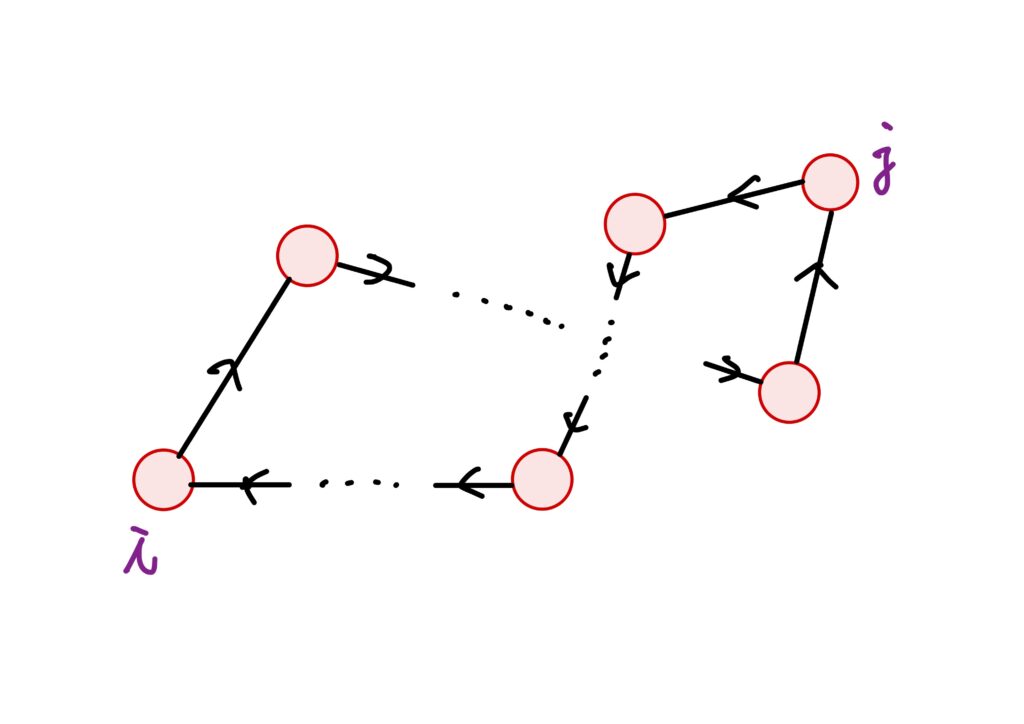
※注意※ 上記のように書くと、「\(\sim\)と書いたらば\(i\)から\(j\)に向かう路と、\(j\)から\(i\)に向かう路が存在することを表している」と捉えられるかもしれませんがそうではありません。
あくまでここでは\(\sim\)を上記のように定める、という話です。
さて、先程定めた関係\(\sim\)は実は同値関係です。
命題2.
与えられた有向グラフの頂点の集合を\(V=\left\{1,\dots,n\right\}\)とし、任意の頂点\(i,j\in V\)に対して定めたこれは同値関係の良い復習になると思われますので、是非一度証明してみて下さい。
命題2.の証明
何を示せばよいかというと、以下の3つです。
- 反射律:\(i\in V\)のとき、\(i\sim i\)である。
- 対称律:\(i,j\in V\)のとき、\(i\sim j\Rightarrow j\sim i\)である。
- 推移律:\(x,y,z\in X\)のとき、\(i\sim j,\ j\sim k\Rightarrow i\sim k\)である。
①反射律の証明
これは、そもそも関係\(\sim\)の定め方で\(\forall i\in V\)に対して\(i\sim i\)としたので、成り立っています。
②対称律の証明
\(i,j\in V\)が\(i\sim j\)であるとします。
このとき、関係\(\sim\)の定め方から、頂点\(i\)から頂点\(j\)に向かう路\(c\)と頂点\(j\)から頂点\(i\)への路\(c^\prime\)が存在するので、\(j\sim i\)です。
③推移律の証明
任意の\(i,j,k\in V\)に対して、\(i\sim j\)かつ\(j\sim k\)であるとします。
すなわち、頂点\(i\)から頂点\(j\)に向かう路\(c_1\)と頂点\(j\)から頂点\(k\)に向かう路\(c_2\)が存在します。
すなわち、\(i=o(c_1)\)かつ\(j=t(c_1)=o(c_2)\)かつ\(k=t(c_2)\)という路\(c_1,c_2\)が存在します。
故に、路\(c_1\)と路\(c_2\)をつなげてできる辺の列\(c_1\cdot c_2\)は、頂点\(i\)から頂点\(k\)に向かう路となっています。
より正確には、\(i=o(c_1)\)かつ\(j=t(c_1)=o(c_2)\)かつ\(k=t(c_2)\)という路\(c_1,c_2\)をそれぞれ\(c_1=(e_1,\dots,e_n)\)、\(c_2=(e^\prime_1,\dots,e^\prime_m)\)と書いたとき、
$$
c_1\cdot c_2=\left( e_1,\dots,e_n,\ e^\prime_1,\dots,e^\prime_m\right)
$$
は\(o(e_1)=i\)かつ\(t(e^\prime_m)=k\)となっているため、\(c_1\cdot c_2\)は頂点\(i\)を始点、頂点\(k\)を終点とする路です。
次に、\(i\sim j\)かつ\(j\sim k\)だから、頂点\(j\)から頂点\(i\)に向かう路\(d_1\)と頂点\(k\)から頂点\(j\)に向かう路\(d_2\)が存在します。
これも先程と同様にして\(d_2\cdot d_1\)は始点を\(k\)、終点を\(i\)とする路です。
従って、推移律が成り立ちます。
命題2.の証明終わり
これで晴れて先程定めた頂点の集合\(V=\left\{1,\dots,n\right\}\)上の関係\(\sim\)は同値関係であることが示されました。
先程定めたこの関係\(\sim\)は同値関係ですので、定理1.から\(V\)を分割すること出来ます。
頂点の集合\(V=\left\{1,\dots,n\right\}\)の分割と強連結成分
\(V\)の分割
さて、先程定めた関係\(\sim\)は同値関係ですので、定理1.から\(V\)を次のように分割することが出来ます。
$$
V=V_1\cup V_2\cup\cdots\cup V_s
$$
だたし、各\(V_a\)は、その中の2頂点\(i,j\)に対して\(i\sim j\)が成り立ち、しかもこの性質を持つ最大のものです。
要するに、各\(V_a\)は関係\(\sim\)による同値類です。
各\(V_a\)は同値類ですから、任意の\(1\leq p,q\leq s\)を満たす自然数\(p,q\)に対して、\(V_p\cap V_q=\emptyset\)であることに注意です。
強連結成分
各\(V_a\)に対して、\(V_a\)の2頂点を結ぶ路上にある辺を全て集めて、\(V_a\)を頂点の集まりとする有向グラフを作ります。
このグラフを\(X_\alpha^o\)で表すことにしましょう。
たとえは次のようなグラフです。
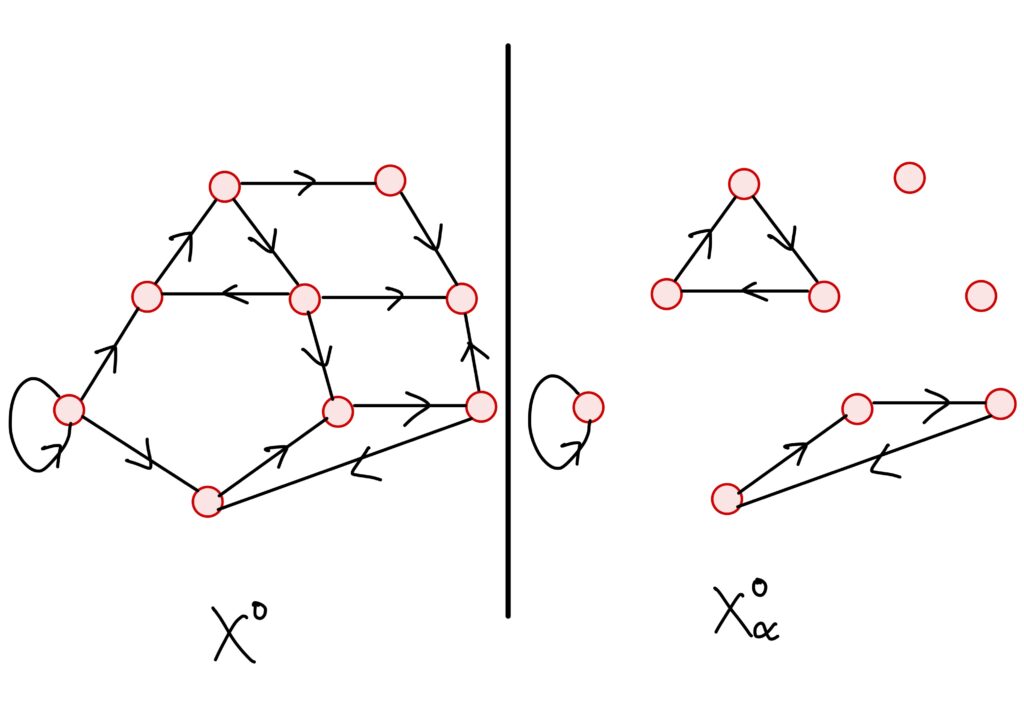
このようにして得られる有向グラフたちは強連結であり、元の有向グラフの強連結成分と呼ばれます。
ここで「お?ということは強連結成分は部分グラフなのね。」となってくれると嬉しいです。
つまり、以下です。
強連結成分
有向グラフ\(X^o\)の強連結な部分グラフ\(X_1^o\)を\(X^o\)の強連結成分という。要するに、強連結な部分は、どの頂点からもどの頂点への路が存在するので、強連結な部分は1頂点と捉えてしまおう、というお話です。
これはまさに、最初に述べた
を表しています。
各強連結成分を1つの頂点と考え、更に強連結成分に属さない辺でそれらを結ぶことで、新しい有向グラフが得られます。

これを\(X_{new}^o\)で表しましょう。
この新しいグラフ\(X_{new}^o\)は「始点と終点が一致する路(閉路)は存在しない」という性質を持っています。
命題3.
\(X_{new}^o\)には閉路が存在しない。命題3.の証明
背理法で証明します。
仮に\(X_{new}^o\)に閉路が存在するとします。
その上には\(X_{new}^o\)の2頂点、例えば\(V_a\)、\(V_b\)が存在します。
閉路を使えば、\(V_a\)に属する元のグラフ\(X^o\)の頂点から\(V_b\)の頂点への路が存在します。
逆に、\(V_b\)に属する頂点から\(V_b\)の頂点の路が存在します。
\(V_a\)と\(V_b\)が強連結であることを使えば、\(V_a\)の頂点\(i\)と\(V_b\)の頂点\(j\)について\(i\sim j\)が成り立つことになります。
これは矛盾です。
命題3.の証明終わり
\(V_1,\dots,V_s\)の順序
次に、\(V_1,\dots,V_s\)に次のような関係\(\leq\)を導入します(ある種の大小関係のようなものです)。
\(V_1,\dots,V_s\)の順序
この関係は次の性質を満たしています。
- \(V_a\leq V_a\)
関係\(\leq\)の定め方から、\(V_a=V_a\)のため、成り立ちます。 - \(V_a\leq V_b,\ V_b\leq V_a\ \Rightarrow\ V_a=V_b\)
\(V_a\leq V_b,\ V_b\leq V_a\)だとしましょう。
このとき\(V_a\)を始点として\(V_b\)を終点とする新しいグラフでの路\(c_1\)が存在し、かつ\(V_b\)を始点として\(V_a\)を終点とする新しいグラフでの路\(c_2\)が存在します。
つまり\(V_a\)の任意の頂点から\(V_b\)の任意の頂点への路が存在し、同時に\(V_b\)の任意の頂点から\(V_a\)の任意の頂点への路が存在するため、\(V_a\cup V_b\)を頂点の集合とする元のグラフの一部は強連結です。
すなわち、今、\(V_a\)と\(V_b\)の要素を頂点とする元のグラフはそれぞれ強連結なため\(V_a\cup V_b\)は強連結成分の頂点の集合です。
故に、\(V_a\subset V_b\)かつ\(V_b\subset V_a \)なので\(V_a=V_b\)です。 - \(V_a\leq V_b,\ V_b\leq V_c\ \Rightarrow\ V_a\leq V_c\)
\(V_a\leq V_b,\ V_b\leq V_c\)とします。
\(V_a=V_b\)であれば、\(V_a=V_b\leq V_c\)となるので成り立ちます。
\(V_b=V_c\)の場合も同様です。
次に、\(V_a\)、\(V_b\)、\(V_c\)のどれもが互いに等しくない場合を考えます。
このとき、\(V_a\)を始点とし\(V_b\)を終点とする新しいグラフでの路\(c_1\)が存在し、かつ\(V_b\)を始点とし\(V_c\)を終点とする新しいグラフでの路\(c_2\)が存在します。
故に、\(c_1\)と\(c_2\)をつなげて出来る\(c_3=c_1\cdot c_2\)は\(V_a\)の要素を始点、\(V_c\)の要素を終点とする路です。
従って、\(V_a\leq V_c\)です。
性質2.は「始点と終点が一致する路(閉路)は存在しない」ということを表現しています。
\(V_a\leq V_b\)で、かつ\(V_a\neq V_b\)であるとき、\(V_a<V_b\)と書くことにしましょう。
先程定めた関係\(\leq \)は数の大小関係と似ていますが、数の場合と違って、全ての\(V_a,\ V_b\)に大小関係があるとはかぎりません。
余談(順序集合)
一般の集合において、その要素たちの関係\(\leq \)が次の性質を満たすとき、\(\leq\)を順序関係といい、順序関係の与えられた集合を順序集合と言います。- \(x\leq x\),
- \(x\leq y,\ y\leq x\ \Rightarrow\ x=y\),
- \(x\leq y,\ y\leq z\ \Rightarrow\ x\leq z\).
\(V_a\)たちの番号付けと\(V_a\)の中の頂点の番号付け
頂点に番号を付けます。
\(V_a\)たちの番号付け
\(V_a\)たちに次の規則で番号を付けます。
- \(V_b<V_a\)となる\(V_b\)が存在しないような\(V_a\)を選び(複数あるかもしれません)、これを極小元といい、これに番号\(1\)を付ける。
複数ある場合は一方を任意に選び番号\(1\)を付ける。 - \(V_a\)を取り除いたものの中で、極小元を選び、それに番号\(2\)を付ける。
- この操作を繰り返す。
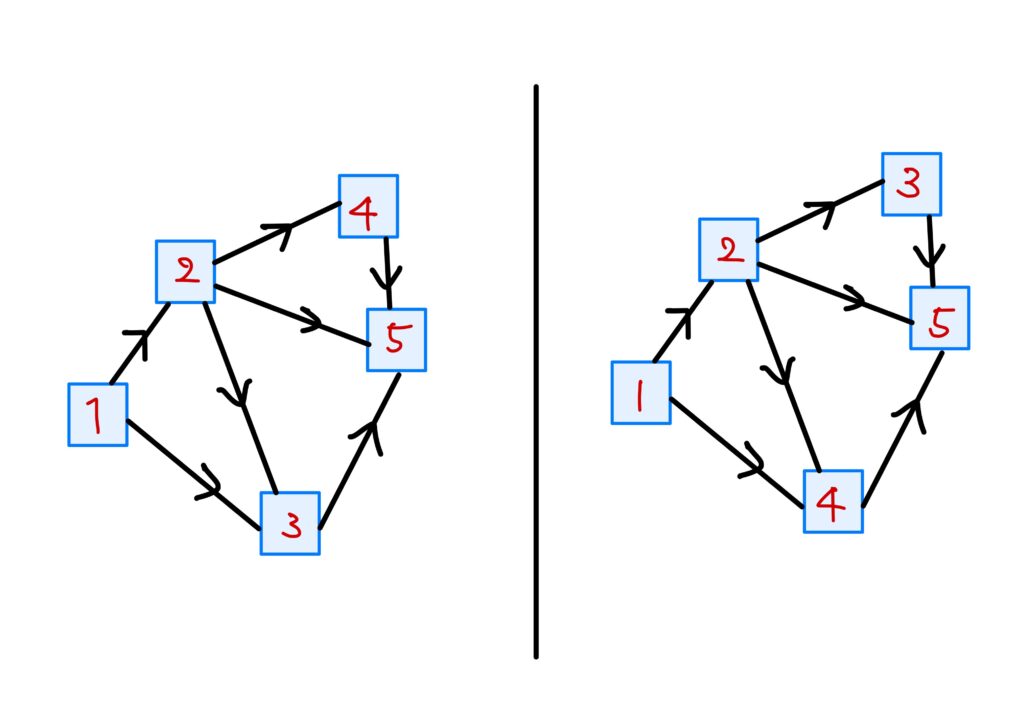
この番号付けと、先程定めた\(\left\{V_a\right\}\)の順序関係\(\leq\)は次のように関連しています。
数の大小関係として\(i\leq j\)が成り立つ(逆は一般に成り立たない)。
そこで、\(V_a\)の番号が\(i\)であるときに、改めて\(V_a\)を\(V_i\)と書くことにしましょう。
先程述べた通り、数として\(i<j\)であるとき、\(V_j\)から\(V_i\)への路は存在しません。
実際、もし\(V_j\)から\(V_i\)への路が存在したとすると、番号の付け方から、\(j\leq i\)となってしまうから矛盾です。
\(V_a\)の中の頂点の番号付け
さらに、各\(V_i\)の頂点の数を\(n_i\)として表し、\(V_i\)の頂点にも次の規則で番号付けします。
- \(V_1\)の頂点には、\(1,2,\dots,n_1\)の番号
- \(V_2\)の頂点には、\(n_1+1,n_1+2,\dots,n_1+n_2\)の番号
\(\vdots\) - 以下同様にして、\(V_s\)の頂点には\(n_1+\cdots+n_{s-1}+1,\ n_1+\cdots+n_{s-1}+2,\dots ,\ n_1+\cdots+n_{s-1}+n_s=n\)の番号
を付けます。
こうして、元々の有向グラフ\(X^o\)の頂点に新しい番号が付けられました。
そこで、新しい番号\(k\)を持つ頂点の要素の番号が\(i_k\)だったとして、置換\(\sigma\)を
$$
\sigma=
\left(\begin{array}{c}
1&2&\cdots&n\\
i_1&i_2&\cdots&i_n\\
\end{array}\right)
$$
で定めます。
ちなみに、置換というのは以下でした。
置換
\(n\in\mathbb{N}\)とする。\(n\)個の文字\(1,2,\dots,n\)からなる集合を $$ M_n=\{1,2,\dots,n\} $$ とする。写像\(\sigma:M_n\to M_n\)が全単射であるとき、\(\sigma\)を\(M_n\)の置換という。置換\(\sigma\)による対応が $$ 1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n $$ であるとする、すなわち、 $$ \sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n $$ とする。このとき\(\sigma\)を $$ \sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix} $$ と書く。
詳しくは、【線型代数学の基礎シリーズ】行列式編 その1を御覧ください。
皆様のコメントを下さい!
今回も数学者ジョークを1つ紹介します。
Aさん「数学者は何故国立公園が好きなの?」
数学者「天然の丸太(natural log=自然対数)があるからだよ。」
logは”丸太”という意味もあるので、こういうジョークが出来たようです。
皆様は他に数学者のジョークをご存知ですか?
是非コメントで教えて下さい!
結
今回は強連結成分について解説しました。
今回の記事は強連結成分について述べたもの、特に目新しいものはなかったと思います。
ある種、次回の準備です。
さて、強連結成分というのは、強連結でないグラフを強連結な部分とそうでない部分にわけ、強連結な部分(部分グラフ)を強連結成分と呼びます。




コメントをする