「行列式のための準備(置換、巡回置換、互換、置換の符号 )」【線型代数学の基礎シリーズ】行列式編 その1

本記事の内容

本記事は行列式を知るために必要な「置換、互換、対称群(サラッと)、巡回置換、置換の符号」について解説する記事です。

本記事を読むにあたり、写像について知っている必要があるため、以下の記事も合わせてご覧ください。

「全単射って？」【論理と集合シリーズ】写像編 その8

...

for-spring.com

2022.03.27

※写像編としてシリーズ化しておりますので、その一部の記事のリンクを掲載しています。
写像編の記事一覧→【論理と集合シリーズ】写像編

置換

では、まず置換(ちかん)について解説します。

置換を一言で

置換を一言でいうと

です。
「対応のこと」と述べているとおり、置換は写像です。
番号の並び替えなわけですので、「$1$を$3$に、$2$も$3$に入れ替える」というのは並び替えではありません。
これを写像の言葉でいうと全単射です。

「全単射？あれ？」となっている方は【論理と集合シリーズ】写像編 その8を御覧ください。

以上のことを数学の言葉で書くと以下になります。

置換って数学の言葉でいうと何スか？

置換の数学の言葉でいうと、次です。

です。
とどのつまり、上段に元の数を並べて、下段に上の数字の行き先を書く、というわけです。
勿論
$$\sigma= \begin{pmatrix} 1&2&\cdots&n \\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\\ \end{pmatrix}$$
と書くこともあります。

置換$\sigma$は全単射ですので、$i_1,i_2,\cdots,i_n$はそれぞれ相異なります。
つまり、順列(順序のついた列)$(i_1,i_2,\cdots,i_n)$が得られる、ということになります。
ちなみに、$(1,2,3)$が順列だったとすると、$(1,2,3)$は$(2,1,3)$やら$(3,1,2)$とは構成されている数字は同じですが、列としては別物です。

逆に、$1,2,\cdots,n$からなる任意の順列$(i_1,i_2,\cdots.i_n)$が与えられたとすると、$1$を$i_2$に、$2$を$i_2$に、これを繰り返して$n$を$i_n$として並び替えるということですので、置換
$$\sigma= \begin{pmatrix} 1&2&\cdots&n \\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\\ \end{pmatrix}$$
が得られます。

と、言うことは、$M_n$の置換全体の集合と$M_n$の順列全体の集合とには一対一対応(全単射)が存在する、ということです。

※注意※置換は$1,2,\dots,n$をそれぞれどのように並び替えるか、という話なので、置換
$$\sigma=\begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix},$$
は上下段の組み合わせが同じであれば、順番を入れ替えても同じ置換を指します。
例えば、
$$\begin{pmatrix} 1&2&3 \\ 3&1&2\\ \end{pmatrix}= \begin{pmatrix} 2&3&1 \\ 1&2&3\\ \end{pmatrix}$$
です。

例えばどんなのッスか？

簡単ではありますが、例をあげます。

例1.置換 $$\sigma= \begin{pmatrix} 1&2&3 \\ 2&1&3\\ \end{pmatrix}$$
としたときを考えます。
このとき、
$$\sigma(1)=2,\ \sigma(2)=1,\ \sigma(3)=3$$
です。
つまり、$1$番目を$2$に、$2$番目を$1$に、$3$はそのまま、という並び替えをしたということで、このとき順列$(2,1,3)$が得られます。

逆に、順列$(2,1,3)$が得られたらば、これは$1$番目を$2$に、$2$番目を$1$に、$3$はそのまま、という並び替えをしたことになりますので、置換
$$\sigma= \begin{pmatrix} 1&2&3 \\ 2&1&3\\ \end{pmatrix}$$
が得られます。

記号のお話

$M_n=\{1,2,\dots,n\}$の置換全体からなる集合を$S_n$と書くことにします。
すなわち、
$$S_n=\left\{ \begin{pmatrix} 1&2&\cdots&n \\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\\ \end{pmatrix}\middle|\sigmaは置換 \right\}$$
です。

例1.を思い出してみましょう。
例1.は平たく言うと$1,2,3$を$(2,1,3)$に並び替える、という話でした。
しかし、$1,2,3$の並び替え方はこれだけではありません。
$(3,2,1)$に並び替えるというパターンもあります。
全部で何パターンあるかというと、単純に順列のお話で$3!=6$パターンあります。

したがって、$1,2,\dots,n$の並び替え方は全部で$n!$個あります。
故に$S_n$の要素の数は$n!$個です。

置換の積

「並び替え方に掛け算？」と思うかもしれませんが、置換には積が定まります。
例えば$2\times 3$のような掛け算のイメージとは少々毛色が違いますが、何ら難しい話ではありません。

というもの、一言で言えば、

です。

ここで、ひとつ全単射の合成写像について話します。

命題2.の証明

①単射の証明

示したいことは、
$$(\forall x,y\in X)\ (g\circ f)(x)=(g\circ f)(y)\Rightarrow x=y$$
です。
今、任意の$x,y\in X$に対して$(g\circ f)(x)=(g\circ f)(y)$とします。
このとき、$g\circ f$は$g$と$f$の合成写像ですので、
$$g\left( f(x)\right)=g\left( f(y)\right)$$
が成り立ちます。
ここで、$g$は全単射ですので、単射です。
故に
$$g\left( f(x)\right)=g\left( f(y)\right)\Rightarrow f(x)=f(y)$$
です。
また、$f$も全単射なので、単射です。
故に
$$f(x)=f(y)\Rightarrow x=y$$
です。
従って、
$$(\forall x,y\in X)\ (g\circ f)(x)=(g\circ f)(y)\Rightarrow x=y$$
です。

②全射の証明

示したいことは、
$$(\forall z\in Z)\ (\exists x\in X)\ {\rm s.t.}\ z=(g\circ f)(x)$$
です。
$g$は全単射ですので、全射です。
故に
$$(\forall z\in Z)\ (\exists y\in Y)\ {\rm s.t.}\ z=g(y)$$
です。
また、$f$は全単射ですので、全単射です。
故に、
$$(\forall y\in Y)\ (\exists x\in X)\ {\rm s.t.}\ y=f(x)$$
です。
このとき、
$$(g\circ f)(x)=g\left(f(x) \right)=g(y)=z$$
となるため、
$$(\forall z\in Z)\ (\exists x\in X)\ {\rm s.t.}\ z=(g\circ f)(x)$$
が成り立ちます。

命題2.の証明終わり

では、置換の積の話に戻ります。

$\tau,\sigma\in S_n$とします。
すなわち、$\tau: M_n\to M_n$かつ$\sigma:M_n\to M_n$でかつ全単射だとします。
このとき、$\tau,\sigma$は全単射ですので、$\tau\circ\sigma:M_n\to M_n$も命題2.から全単射です。
従って、$\tau\circ\sigma\in S_n$です。

これをしっかり書くと次です。

次に置換の積を
$$\sigma=\begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$$
の形で書いてみましょう。

$$\sigma=\begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix},\quad \tau=\begin{pmatrix} 1&2&\cdots&n \\ j_1&j_2&\cdots&j_n\\ \end{pmatrix}$$
と書いたとしましょう。
※注意※で述べたとおり、置換は上下段の組み合わせが同じであれば置換として同じものですので、$\tau$の上段を$\sigma$から得られる順列$(i_1,i_2,\dots,i_n)$に並び替えても$\tau$と一致しています。
つまり、
$$\tau=\begin{pmatrix} 1&2&\cdots&n \\ j_1&j_2&\cdots&j_n\\ \end{pmatrix}= \begin{pmatrix} j_1&j_2&\cdots&j_n\\ r_1&r_2&\cdots&r_n\\ \end{pmatrix}$$
です。
このように$\tau$を書き直したとき、$\sigma$と$\tau$の積$\tau\sigma$
$$\tau\sigma= \begin{pmatrix} j_1&j_2&\cdots&j_n\\ r_1&r_2&\cdots&r_n\\ \end{pmatrix} \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$$
は
$$1\mapsto i_1\mapsto r_1,\ 2\mapsto i_2\mapsto r_2,\dots,\ n\mapsto i_n\mapsto r_n$$
ということですので、
$$\tau\sigma= \begin{pmatrix} j_1&j_2&\cdots&j_n\\ r_1&r_2&\cdots&r_n\\ \end{pmatrix} \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}= \begin{pmatrix} 1&2&\cdots&n \\ r_1&r_2&\cdots&r_n\\ \end{pmatrix}$$
となります。
$i_1,i_2,\dots,i_n$、$j_1,j_2,\dots,j_n$および$r_1,r_2,\dots,r_n$をそれぞれ写像の記号を使って書くと、

• $(i_1,i_2,\dots,i_n)=(\sigma(1),\sigma(2),\dots,\sigma(n))$、
• $(j_1,j_2,\dots,j_n)=(\tau(1),\tau(2),\dots,\tau(n))$、
• $(r_1,r_2,\dots,r_n)=(\tau(i_1),\tau(i_2),\dots,\tau(i_n))$

です。
特に、$(i_1,i_2,\dots,i_n)=(\sigma(1),\sigma(2),\dots,\sigma(n))$ですので、
$$r_1=\tau(\sigma(1)),\ r_2=\tau(\sigma(2)),\dots,\ r_n=\tau(\sigma(n))$$
となります。
すなわち、
$$\begin{eqnarray} \tau\sigma&=& \begin{pmatrix} 1&2&\cdots&n \\ j_1&j_2&\cdots&j_n\\ \end{pmatrix} \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix} \\ &=& \begin{pmatrix} 1&2&\cdots&n \\ \tau(1)&\tau(2)&\cdots&\tau(n)\\ \end{pmatrix} \begin{pmatrix} 1&2&\cdots&n \\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\\ \end{pmatrix} \\ &=& \begin{pmatrix} \sigma(1)&\sigma(2)&\cdots&\sigma(n) \\ \tau(\sigma(1))&\tau(\sigma(2))&\cdots&\tau(\sigma(n))\\ \end{pmatrix} \begin{pmatrix} 1&2&\cdots&n \\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&\cdots&n \\ \tau(\sigma(1))&\tau(\sigma(2))&\cdots&\tau(\sigma(n))\\ \end{pmatrix} \end{eqnarray}$$
となります。

次に、置換の積を具体的に計算してみましょう！

例3.
$$\sigma=\begin{pmatrix} 1&2&3&4 \\ 3&2&4&1\\ \end{pmatrix},\quad \tau=\begin{pmatrix} 1&2&3&4 \\ 2&1&4&3\\ \end{pmatrix}$$
の積$\tau\sigma$を考えます。

• $\tau(\sigma(1))=\tau(3)=4$、
• $\tau(\sigma(2))=\tau(2)=1$、
• $\tau(\sigma(3))=\tau(4)=3$、
• $\tau(\sigma(4))=\tau(1)=2$

となるので、
$$\tau\sigma= \begin{pmatrix} 1&2&3&4 \\ 4&1&3&2\\ \end{pmatrix}$$
です。

余談(対称群)

実は$S_n$は「群」と呼ばれるものになります。
この$S_n$は対称群(または置換群)と呼ばれます。
「群？ﾅﾝｼﾞｬｿﾚ?」という感じでしょうが、サラッと(本当にサラッと)いうと、結合則、単位元の存在、逆元の存在が保証されている演算が定まっている集合です。
例えば、単位元の存在というのは掛け算でいうところの$1$で、足し算でいうとことの$0$です。
逆元の存在については、掛け算で言うところの掛けて$1$になる数(例えば$2$に対して$\displaystyle\frac{1}{2}$が$2$の逆元)、足し算で言うところの足して$0$になる数です(例えば、$5$に対して$-5$が$5$の逆元)。
整数の集合$\mathbb{Z}$は足し算において群ですが、$\mathbb{N}$は足し算で群ではありません。
実際、自然数同士を引き算すると値が負になることもあるので、自然数ではなくなってしまうからです。
つまり、自然数の範囲では逆元が存在しない場合があるからです。
また、$\mathbb{Z}$は足し算については群ですが、掛け算については群ではありません。
実際、自然数のときと同様に整数同士を割り算すると整数でなくなる場合もあるからです。
つまり、整数の範囲では逆元が存在しない場合があるからです。

巡回置換

巡回置換は、置換の中で特別な性質を持つ置換のことです。
何に使うか？というと勿論行列式の話をするために必要なのですが、特に「置換の符号」というものを考えるために使います。

巡回置換を一言で

巡回置換を一言で述べれば、

です。
「まんまじゃねえか」と思うかもしれませんが、実際そうなのです。

例えばどんなのッスか？

例を挙げましょう。

例4.
$$\sigma= \begin{pmatrix} 1&2&3&4&5 \\ 5&2&1&4&3\\ \end{pmatrix}$$
とします。
このとき、
$$\sigma(1)=5,\ \sigma(2)=2,\ \sigma(3)=1,\ \sigma(4)=4,\ \sigma(5)=3$$
で、$2$と$4$は順番を並び替えずに、$1\mapsto 5$、$5\mapsto 3$、$3\mapsto 1$というように、$1$が$5$と$3$を経由してグルッと回ってて$1$に戻ってくるということです。
それ故、巡回置換と呼ばれます。

で、巡回置換って何スか？

以上のことをしっかり書くと次です。

先程の例4.においては、$\sigma=(1\ 5\ 3)$です。
また、巡回置換はぐるぐる回るので、まわり方の順番が変わらなければ、巡回置換として同じものなので、$(5\ 3\ 1)$やら$(3\ 1\ 5)$と書くこともできます。

置換と巡回置換との関係

実は、どんな置換であっても、置換は巡回置換の積で書き表すことができます。
つまり、以下が成り立ちます。

定理5.の証明

任意の置換$\sigma=\begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$が与えられたとき、まず、何か１つの文字を、例えば$1$をとり、それが次々とどのように移っていくのかを見ます。

すると、
$$1\mapsto j_1,\ j_1\mapsto j_2,\ j_2\mapsto j_3,\cdots$$
と書いたとき、この移り変わり(並び替え)は集合$M_n=\{1,2,\dots,n\}$の部分集合の要素をぐるっとまわて$1$に戻ってくるはずです。
そこで、今、仮に$1$に戻ってこないとして矛盾を導きます(背理法！)。

$M_n$の要素の数はあくまで有限ですので、無限に次々と新しい数が登場することはありません。
従って、あるときに今まで登場した数が再び登場します。
同じ数が再びでるその最初の数が$1$以外だとして、その数を$j_k$とします。

つまりどういうことかというと、次の図です。

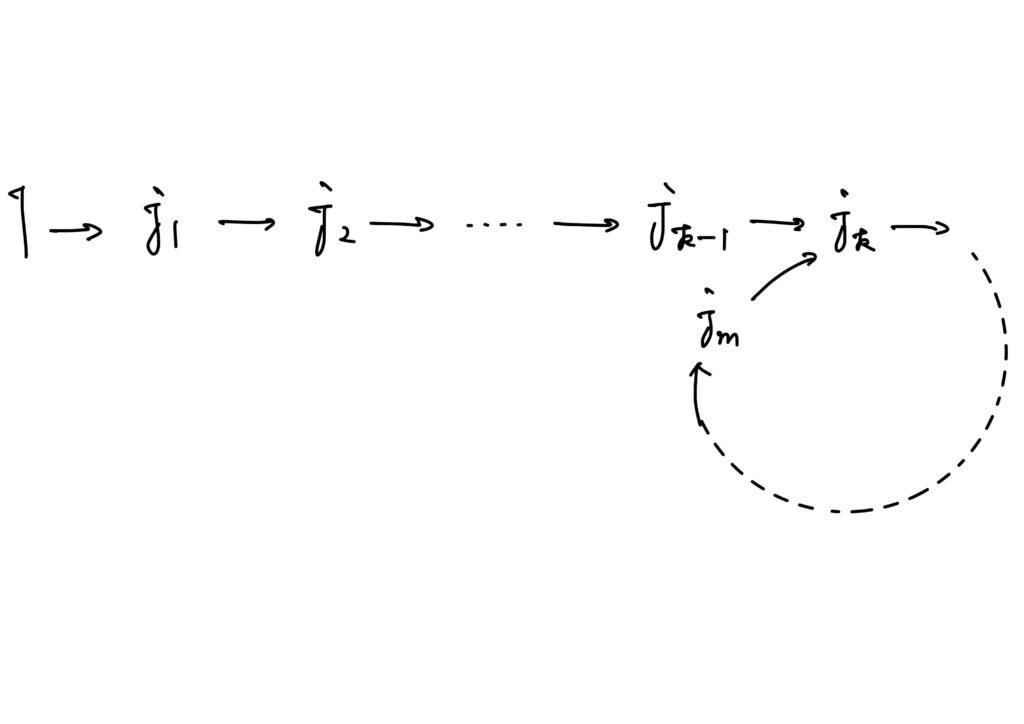
このように、$j_{k-1}\mapsto j_k$であり、かつ$j_m\to j_k$です。
ここで重要なのが、「置換は全単射である」ということです。
今、$j_{k-1}\mapsto j_k$であり、かつ$j_m\mapsto j_k$ということで、$\sigma(j_{k-1})=\sigma(j_m)=j_k$ということになり、$\sigma$が単射でなくなってしまいましたので矛盾です。
故に、戻ってくる数は必ず$1$となります。
このことから、巡回置換$(1\ j_1\ j_2\ \cdots\ j_{k-1})$が定まります。

次に、残った文字について同じように考えれば、巡回置換が次々と得られます。
この操作は$M_n$の要素が有限個しかないので、有限回で終了します。
これはすなわち、置換は有限個の巡回置換の積で書けるということを表しています。

一意性についても簡単です。
ある置換を別の巡回置換の積で書いたとします。
別の巡回置換の積で書いたということは、巡回の仕方(どの数でぐるぐる回っているか)が異なるということです。
ということは、あるときに別々の数が同じ数を経由して新たな数へ向かう、ということが起こります。
これは置換の全単射性、特に単射性に反しますので一意的です。

定理5.の証明終わり

定理5.が本当に成り立つかをいっちょ計算してみましょう。

例6.$\sigma=\begin{pmatrix} 1&2&3&4&5&6&7&8&9 \\ 3&7&4&5&1&9&8&2&6\\ \end{pmatrix}$としたとき、どのように巡回置換の積で書けるか、ということを順々に見ていきます。
まずは$1$です。
$$1\mapsto 3,\ 3\mapsto 4,\ 4\mapsto 5,\ 5\mapsto 1$$
となるので、$1$から始まってぐるっと回る巡回置換は$(1\ 3\ 4\ 5)$です。
これをより厳密に捉えると、$1\to3\to4\to5\to1$という置換で、$2,6,7,8,9$については並び替えないような置換、すなわち、
$$(1\ 3\ 4\ 5)= \begin{pmatrix} 1&3&4&5&2&6&7&8&9\\ 3&4&5&1&2&6&7&8&9\\ \end{pmatrix}$$
ということです。
次に$1,3,4,5$以外の数、例えば$2$を見てみましょう。
すると、
$$2\mapsto 7,\ 7\mapsto 8,\ 8\mapsto 2$$
となるので、$2$から始まってぐるっと回る巡回置換は$(2\ 7\ 8)$です。
これをより厳密に捉えると、$2\to7\to8\to2$という置換で、$1,3,4,5,6,9$については並び替えないような置換、すなわち、
$$(2\ 7\ 8)= \begin{pmatrix} 2&7&8&1&3&4&5&6&9\\ 7&8&2&1&3&4&5&6&9\\ \end{pmatrix}$$
ということです。
残った$6$と$9$を見れば、$6\to9\to6$ということで、
$$(6\ 9)= \begin{pmatrix} 6&9&1&2&3&4&5&7&8\\ 9&6&1&2&3&4&5&7&8\\ \end{pmatrix}$$
が得られます。
これらの積をとってみましょう。

$$\begin{eqnarray} &&(1\ 3\ 4\ 5)(2\ 7\ 8)(6\ 9)\\ &=& \begin{pmatrix} 1&3&4&5&2&6&7&8&9\\ 3&4&5&1&2&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 2&7&8&1&3&4&5&6&9\\ 7&8&2&1&3&4&5&6&9\\ \end{pmatrix} \begin{pmatrix} 6&9&1&2&3&4&5&7&8\\ 9&6&1&2&3&4&5&7&8\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&4&5&1&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 1&7&3&4&5&6&8&2&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 1&2&3&4&5&9&7&8&6\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&4&5&1&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 1&7&3&4&5&9&8&2&6\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&7&4&5&1&9&8&2&6\\ \end{pmatrix}=\sigma \end{eqnarray}$$
となって、巡回置換の積で表すことができました。

※注意※巡回置換は「どこでぐるぐる回るか」ということが重要なので、ぐるぐる回っている塊の順序が変わっても置換としてはおなじものを指します。

例6.でいうところの
$$\sigma=(1\ 3\ 4\ 5)(2\ 7\ 8)(6\ 9)=(2\ 7\ 8)(1\ 3\ 4\ 5)(6\ 9)=(2\ 7\ 8))(6\ 9)(1\ 3\ 4\ 5$$
が成り立ちます(面倒くさいけど計算してみると分かります)。

互換

互換はある条件下の巡回置換です。
つまり、互換は巡回置換の一部ということです。

互換を一言で

超簡単です。

つまり、$M_n$の中で、特定の2つを入れ替えて、あとはそのまま、という置換のことで、これは巡回置換でもあります。
例6.でいうところの$(6\ 9)$にあたります。

で、互換って何スか？

ではしっかり書きましょう。

先も述べましたが、とどのつまり、ある特定の２つだけを並び替えてそれ以外はそのまま、という巡回置換のことを互換といいます。

互換と巡回置換の関係

実は、どんな巡回置換でも、互換の積で書くことができます。
つまり、以下が成り立ちます。

この証明は書くのが面倒なだけで、難しくはありません。

定理7.の証明

$(i_1\ i_2\ \cdots\ i_m)$を巡回置換とします。
$$\begin{eqnarray} &&(i_1\ i_m)(i_1\ i_{m-1})\cdots(i_1\ i_3)(i_1\ i_2)\\ &=& \begin{pmatrix} i_1&i_m&i_2&\cdots&i_{m-1}\\ i_m&i_1&i_2&\cdots&i_{m-1}\\ \end{pmatrix} \begin{pmatrix} i_1&i_{m-1}&i_2&\cdots&i_{m-2}&i_{m}\\ i_{m-1}&i_1&i_2&\cdots&i_{m-2}&i_m\\ \end{pmatrix} \\ &&\cdots \begin{pmatrix} i_1&i_3&i_2&i_4&\cdots&i_{m}\\ i_3&i_1&i_2&i_4&\cdots&i_m\\ \end{pmatrix} \begin{pmatrix} i_1&i_2&i_3&\cdots&i_{m}\\ i_2&i_1&i_3&\cdots&i_m\\ \end{pmatrix} \end{eqnarray}$$
となるので、これを順々にどの数がどの数に対応しているのかを見ていけば、
$$i_1\mapsto i_2,\ i_2\mapsto i_3,\ i_3\mapsto i_4,\cdots,i_{m-1}\mapsto i_m,\ i_m\mapsto i_1$$
となるので、
$$\begin{eqnarray} &&(i_1\ i_m)(i_1\ i_{m-1})\cdots(i_1\ i_3)(i_1\ i_2)\\ &=& \begin{pmatrix} i_1&i_2&i_3&\cdots&i_{m}\\ i_2&i_3&i_4&\cdots&1\\ \end{pmatrix} \end{eqnarray}$$
となるため、成り立ちます。

定理7.の証明終わり

例6.に出現した$(1\ 3\ 4\ 5 )$を互換の積に分けてみましょう。
定理通りに行えば、形式的に「$(1\ 5)(1\ 4)(1\ 3)$」と求まるのですが、一度手を動かしてみることをおすすめします。

$$\begin{eqnarray} (1\ 3\ 4\ 5 )&=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&4&5&1&6&7&8&9\\ \end{pmatrix} \end{eqnarray}$$
であることに注意します。
$$\begin{eqnarray} (1\ 5)(1\ 4)(1\ 3)&=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 5&2&3&4&1&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 4&2&3&1&5&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&1&4&5&6&7&8&9\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 5&2&3&4&1&6&7&8&9\\ \end{pmatrix} \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&4&1&5&6&7&8&9\\ \end{pmatrix}\\ &=& \begin{pmatrix} 1&2&3&4&5&6&7&8&9\\ 3&2&4&5&1&6&7&8&9\\ \end{pmatrix}=(1\ 3\ 4\ 5) \end{eqnarray}$$

となります。

置換と互換の関係

定理5.および定理7.から次が言えます。

置換の符号

最後に置換の符号です。
行列式というものの話をする際にキーとなるのが置換の符号です。
「数の並び替えに符号って…ﾅﾝｼﾞｬｿﾚ」と思われるかもしれませんが、なんてことありません。

定理8.から、どんな置換でも、必ず互換の積で書けます。
置換が何個の互換の積で書けるか、ということで置換の符号を定めます。
置換が

• 偶数個の互換の積で表されるときに置換の符号$=1$、
• 奇数個の互換の積で表されるときに置換の符号$=-1$

と定めます。
つまり、以下です。

「本当にこれでいいの？」と思うかもしれませんが、これでOKです。
なぜか、ということを話すと多項式の変化やら差積といったことを話さなければならず、話がずれてしまいますので省略します。

余談

正直、筆者は${\rm sgn}$は行列式以外では殆ど見たことがありません。
それ故、「${\rm sgn}$は行列式のためにあるのかな」なんて思ってます。

この置換の符号について次が成り立ちます。

定理9.の証明の前に恒等置換と逆置換について話します。

定理9.の証明

簡単です。
(1.の証明)

定理8.により、$\sigma$と$\tau$は互換の積で表されるので、
$$\sigma=\sigma_r\sigma_{r-1}\cdots\sigma_1,\quad \tau=\tau_s\tau_{s-1}\cdots\tau_1$$
と書いたとします。
このとき、
$${\rm sgn}(\sigma)=(-1)^r,\quad {\rm sgn}(\tau)=(-1)^s$$
です。
そして、
$$\tau\sigma=\tau_s\tau_{s-1}\cdots\tau_1\sigma_r\sigma_{r-1}\cdots\sigma_1$$
となるので、
$${\rm sgn}(\tau\sigma)=(-1)^{s+r}=(-1)^s(-1)^r={\rm sgn}(\tau){\rm sgn}(\sigma)$$
となります。

(2.の証明)

$\sigma\sigma^{-1}=\epsilon$が成り立ちますので、1.から
$${\rm sgn}(\epsilon)={\rm sgn}(\sigma\sigma^{-1})={\rm sgn}(\sigma){\rm sgn}(\sigma^{-1})=1$$
です。
ここで、一般に置換$\sigma$に対して${\rm sgn}(\sigma)$は$1$か$-1$で、今、${\rm sgn}(\sigma){\rm sgn}(\sigma^{-1})=1$ですので、

• ${\rm sgn}(\sigma)={\rm sgn}(\sigma^{-1})=1$
• ${\rm sgn}(\sigma)={\rm sgn}(\sigma^{-1})=-1$

のいずれか一方が成り立ちます。
故に、
$${\rm sgn}(\sigma^{-1})={\rm sgn}(\sigma)$$
です。

定理9.の証明終わり

次に置換は巡回置換の積で書け、その巡回置換は互換の積で書けることから、巡回置換の符号について以下が成り立ちます。

定理10.の証明

一瞬で終わります。
定理7.から巡回置換$(i_1\ i_2\cdots i_m)$は
$$(i_1\ i_2\ \cdots\ i_m)=(i_1\ i_m)(i_1\ i_{m-1})\cdots(i_1\ i_3)(i_1\ i_2)$$
と書くことができますので、
$$\begin{eqnarray} {\rm sgn}((i_1\ i_2\cdots i_m))&=& {\rm sgn}((i_1\ i_m)(i_1\ i_{m-1})\cdots(i_1\ i_3)(i_1\ i_2))\\ &=&(-1)^{m-1} \end{eqnarray}$$
が成り立ちます。

結

今回は行列式を知るために必要な置換、巡回置換、互換、置換の符号についてエクストリームに解説しました。

置換というのは結局番号をどの順番で並び替えるか、という話であって、これは写像です。
さらに並び替えるわけですので、同じ番号が複数出てくることはありません。
従って全単射です。

また、置換であって並び替え方がぐるぐる回るような置換を巡回置換といいます。
さらに置換は巡回置換の積で書かれ、巡回置換は互換の積で書かれるので、置換は互換の積で書かれます。

その互換の数に注目して置換の符号を定めました。

次回はいよいよ行列式とは何か、その性質の１部を解説します。

乞うご期待！質問、コメントなどお待ちしております！