本記事の内容
本記事は有限アーベル群の基本定理の証明を順を追って解説する記事です。
本記事を読むに当たり、アーベル群、位数、同型、中国式剰余定理について知っている必要があるため、以下の記事も合わせてご覧ください。
↓アーベル群の記事
↓位数の記事
↓同型の記事
↓中国式剰余定理の記事
数回に渡ってやること
【代数学の基礎シリーズ】群論編 その36から数回に渡って何をするかというと、結論としては、以下の定理を証明します。
定理0.(有限アーベル群の基本定理)
\(G\)が有限なアーベル群ならば、整数\(e_1,\dots,e_n\geq2\)が存在して、\(i=1,\dots,n-1\)に対して\(e_i|e_{i+1}\)を満たし、 $$ G\cong \mathbb{Z}/{e_1\mathbb{Z}}\times\cdots\times\mathbb{Z}/{e_n\mathbb{Z}} $$ となる。また、この条件を満たす\(e_1,\dots,e_n\)は一意的に定まる。ただし、\(n=0\)のときは\(G\cong\left\{0\right\}\)と解釈する。有限アーベル群の基本定理は何を言っているのか?
要するに、有限アーベル群の基本定理は何を言っているのか、というと
ということです。
もっと平たく言えば、「有限なアーベル群は”いい具合に”商群の直積に分解することができる」ということです。
証明の流れ
主張を言い換えてみます。
\(e\geq2\)を整数とすれば、相異なる素数\(p_1,\dots,p_t\)により\(e=p_1^{a_1}\cdots p_t^{a_t}\)と素因数分解できます。
ここで、中国式剰余定理を使います。
定理1.(中国式剰余定理)
\(m,n\neq 0\)が互いに素な整数ならば、 $$ \mathbb{Z}/{mn\mathbb{Z}}\cong \mathbb{Z}/{m\mathbb{Z}}\times\mathbb{Z}/{n\mathbb{Z}} $$ である。定理1.(中国式剰余定理)の証明は【代数学の基礎シリーズ】群論編 その28を御覧ください。
中国式剰余定理を使うことで、
$$
\mathbb{Z}/{e\mathbb{Z}}\cong\mathbb{Z}/{p_1^{a_1}\mathbb{Z}}\times\cdots\times\mathbb{Z}/{p_t^{a_t}\mathbb{Z}}
$$
です。
したがって、有限アーベル群の基本定理の\(G\)は位数が素数べきの巡回群の積で表されることになります。
そこで、有限アーベル群の基本定理の代わりに、次の定理を証明することにします。
その証明の跡で、有限アーベル群の基本定理が以下の定理から従うことを示します。
定理00.(有限アーベル群の基本定理2)
\(G\)を有限なアーベル群とするとき、次の1.、2.が成り立つ。- 素数\(p_1,\cdots,p_t\)(重複を許す)と正の整数\(a_1,\cdots,a_t\)が存在して $$ \mathbb{Z}/{e\mathbb{Z}}\cong\mathbb{Z}/{p_1^{a_1}\mathbb{Z}}\times\cdots\times\mathbb{Z}/{p_t^{a_t}\mathbb{Z}} $$ となる。また、\(p_1^{a_1},\cdots,p_t^{a_t}\)は順序を除いて一意的に定まる。
- 素数\(p\)に対して、\(G(p)\)を\(p_i=p\)である\(i\)全てに属する\(\mathbb{Z}/{p_i^{a_i}\mathbb{Z}}\)の直積とすると、\(G\)は全ての\(G(p)\)の直積であり、\(G(p)\)は\(G\)のシロー\(p\)部分群である。
定理00.(有限アーベル群の基本定理2)の証明の流れ
- 同型写像の存在
- \(\left|G\right|\)が\(p\)ベキであることの証明→【代数学の基礎シリーズ】群論編 その36で証明済み
- \(G\)が巡回群の直積となることの証明→【代数学の基礎シリーズ】群論編 その37で証明済み
- 同型写像を作る。→【代数学の基礎シリーズ】群論編 その39で証明済み
- 存在する整数の一意性
- 上の分解が直積因子の順序を除き一意的であることの証明→【代数学の基礎シリーズ】群論編 その39で証明済み
- 一般の場合の直積因子の一意性の証明→【代数学の基礎シリーズ】群論編 その40を御覧ください。
今回は、いよいよ、定理00.を用いて定理0.(有限アーベル群の基本定理)を証明します。
有限アーベル群の基本定理の証明に入る前に(例)
定理00.から定理0.を証明しますが、次の例題で簡単な場合を試してから一般の場合について解説することにします。
\(G=\mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{4\mathbb{Z}}\times\mathbb{Z}/{4\mathbb{Z}}\times\mathbb{Z}/{9\mathbb{Z}}\times\mathbb{Z}/{27\mathbb{Z}}\times\mathbb{Z}/{5\mathbb{Z}}\)とするとき、\(G\)を定理0.(有限アーベル群の基本定理)の主張の形で書け。
解答
定理0.の主張の\(e_t\)の方から定めます。
各素数(つまり、\(2,3,5\)のどれか)ベキの最大の部分を取り出せば、
$$
\mathbb{Z}/{4\mathbb{Z}}\times\mathbb{Z}/{27\mathbb{Z}}\times\mathbb{Z}/{5\mathbb{Z}}\cong\mathbb{Z}/{540\mathbb{Z}}
$$
です(同型は中国式剰余定理より)。
残りは、\(\mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{4\mathbb{Z}}\times\mathbb{Z}/{9\mathbb{Z}}\)なので、次の因子は\(\mathbb{Z}/{4\mathbb{Z}}\times\mathbb{Z}/{9\mathbb{Z}}\cong\mathbb{Z}/{36\mathbb{Z}\)です。
のこりは\(\mathbb{Z}/{2\mathbb{Z}}\)だけです。
したがって、
$$
G\cong \mathbb{Z}/{2\mathbb{Z}}\times\mathbb{Z}/{36\mathbb{Z}}\times\mathbb{Z}/{540\mathbb{Z}}
$$
です。
解答終わり
いざ、有限アーベル群の基本定理の証明
主張の再掲
定理0.(有限アーベル群の基本定理)
\(G\)が有限なアーベル群ならば、整数\(e_1,\dots,e_n\geq2\)が存在して、\(i=1,\dots,n-1\)に対して\(e_i|e_{i+1}\)を満たし、 $$ G\cong \mathbb{Z}/{e_1\mathbb{Z}}\times\cdots\times\mathbb{Z}/{e_n\mathbb{Z}} $$ となる。また、この条件を満たす\(e_1,\dots,e_n\)は一意的に定まる。ただし、\(n=0\)のときは\(G\cong\left\{0\right\}\)と解釈する。有限アーベル群の基本定理の証明
\(G\)を有限アーベル群とします。
素数\(p\)に対して、\(G(p)\)を\(G\)の要素で位数が素数べきであるもの全体の集合とします。
定理00.の2.により、\(G\)が\(G(p_1),\dots,G(p_l)\)の直積となるような有限個の素数\(p_1,\dots,p_l\)が存在します。
$$
G(p_i)=\mathbb{Z}/{p_i^{a_{i1}}\mathbb{Z}}\times\cdots\mathbb{Z}/{p_i^{a_{it_i}}\mathbb{Z}},\quad a_{i1}\leq\cdots\leq a_{it_i}
$$
とします。
ここで、\(t_i\)は\(G(p_i)\)の直積因子の数です。
\(t_1,\cdots,t_l\)の最大値を\(t\)とします。
仮に、\(a_{ij}=0\)だったとすると、
$$
G(p_i)=\mathbb{Z}/{p_i^{a_{i1}}\mathbb{Z}}\times\cdots\mathbb{Z}/{p_i^{a_{it}}\mathbb{Z}},\quad a_{i1}\leq\cdots\leq a_{it}
$$
と表すことができます。
例えば、\(t=2\)で\(G(p_i)=\mathbb{Z}/{p_i^2\mathbb{Z}}\)ならば、これを\(G(p_i)=\mathbb{Z}/{p_i^0\mathbb{Z}}\times\mathbb{Z}/{p_i^0\mathbb{Z}}\)とみなしているということです。
$$
e_j=\prod_{i=1}^lp_i^{a_ij}
$$
とすると、任意の\(j\)に対して\(e_j|e_{j+1}\)であり、\(G\cong \mathbb{Z}/{e_1\mathbb{Z}}\times\cdots\times\mathbb{Z}/{e_t\mathbb{Z}}\)です。
逆に、\(G\cong \mathbb{Z}/{e_1\mathbb{Z}}\times\cdots\times\mathbb{Z}/{e_t\mathbb{Z}}\)となったとしましょう。
\(p_1,\dots,p_l\)を\(\left|G\right|\)を割る全ての素因数とします。
\(\displaystyle e_j=\prod_{i=1}^lp_i^{a_ij}\)と素因数分解すれば、\(\mathbb{Z}/{p_i^{a_{i,t-j+1}}\mathbb{Z}}\)は\(G(p_i)\)に現れる直積因子の中で、位数が\(j\)番目に大きいものです。
無論\(G(p_i)\)の直積因子が\(t_i<t\)子しか存在しなければ、\(j\leq t-t_i\)ならば\(a_{ij}=0\)です。
\(G(p_i)\)の直積因子は、定理00.により一意的に定まるわけですので、\(e_j\)の素因数分解は\(G\)にのみ依存します。
皆様のコメントを下さい!
前回の続きで極限の論法、特に微積分学の歴史について少々語ります。
17世紀の終わり近くにニュートンとライプニッツにより独立に切り開かれました。
彼らは、独立に無限小解析(微分積分学)を創造し、一般的な方法により接線の問題(微分学)と求積(quadrature)の問題(積分学)を扱うことに成功したのです。
前回はニュートンとライプニッツのそれぞれの方法について語りました。
今回は、\(\varepsilon-\delta\)論法以前の極限についてお話します。
曲線\(G\)上の点\(p\)における接線を求めるのに、\(p\)に「近づく」\(C\)上の点\(q\)を取ります。
\(p\)と\(q \)通るような直線\(l_q\)が直線\(l\)に「近づく」とき、\(l\)を\(p\)における\(C\)の接線と定めます。
これは代入や消去などの「代数的操作」により行われる定め方とはまったく異なるものです。
すなわち、1つの点を選ぶことにより接線を定めることはできないので、\(p\)に「近づく」点の列\(q_n\)を想像しているのです。
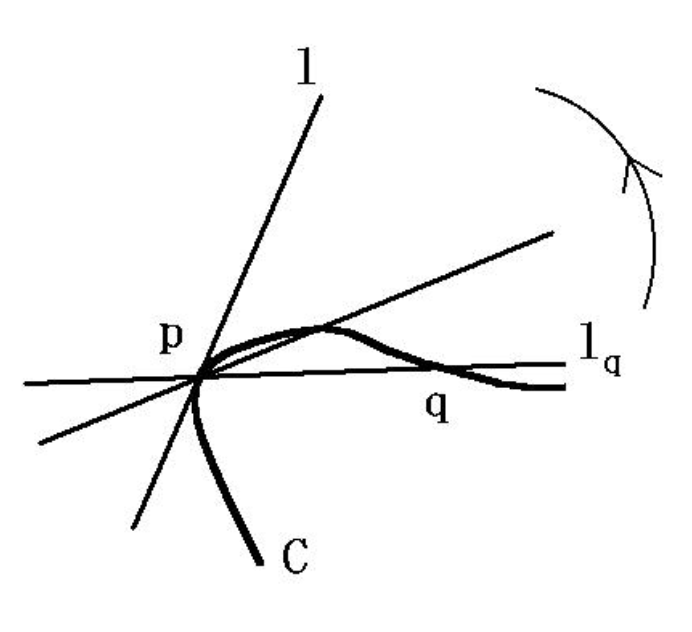
この定め方において「近づく」という言葉が使われています。
この意味は何でしょうか?
「近づく」は日常使う言葉としてまったく問題なく理解されています。
例えば「車が交差点に近づく」、「アキレスが亀に近づく」というようにです。
何故こんな疑問を呈するのかといえば、「近づく」という言葉は数学用語としては曖昧だからです。
もし、「近づく」を数学で使われる「収束する」と言い換えても、言葉の言い換えだけなら何も解決されません。
このような状況はユードクソスとアルキメデスの真の「後継者」とも考えられるニュートン、ライプニッツの登場後も同じでした。
すなわち、無限小解析の初期の段階では、数学者はユードクソスの厳密な定式化に立ち戻ることはなかったのです。
例えば次のような言明の扱いの中に、当時の考え方の限界を見ることができます。
\(\Delta x(\neq0)\)が\(0\)に近づくとき、商 $$ \frac{f(x+\Delta x)-f(x)}{\Delta x}\tag{\ast} $$ は\(a\)に近づく。
仮に\(\Delta x=0\)を\((\ast)\)に代入することができれば、この文章のいみについて思い悩む必要はありません。
しかし、\(\displaystyle\frac{0}{0}\)には意味を与えることができないので、ニュートン、ライプニッツの先駆者であったフェルマーとバーロウ(I. Barrow; 1630-1677)は次のように考えました。
例えば、\(f(x)=x^2\)に対しては、
$$
\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x)^2-x^2}{\Delta x}=2x+\Delta x
$$
であるから、\(\Delta x=0\)として、\(a=2x\)を得ます。
今回はここまで。
感想などコメントをお待ちしております!
結
今回は、有限アーベル群の基本定理の証明の一部を解説しました。
有限アーベル群の基本定理は、「任意の有限アーベル群が巡回群の直積に同型である」という主張の定理です。
今回は、有限アーベル群の基本定理の証明を完結させました。
次回は交代群に焦点を当てます。
乞うご期待!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない!」などいただければお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ一週間以内にお答えします。







コメントをする