本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
では、問題
今回は前回の最後に「皆様への挑戦状」ということで提示した問題です。
図形の問題です。
正三角形\(ABC\)の辺\(BC\)上に点\(D\)を、\(BD:DC=2:1\)にとり、線分\(AD\)上に点\(E\)を\(AE:ED=3:4\)にとれば、\(\angle BED\)、\(\angle CED\)はそれぞれどんな角になるでしょうか。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13.
いざ、チャレンジ
チャレンジの結果、解けました。
今までの1時間チャレンジの中で最も早く解けました。
30分くらいで解けました。
筆者の解答
筆者はこの問題を見た瞬間に「メネラウスの定理とチェバの定理を使って各辺の長さの比を求めて、特別な三角形(正三角形やら直角三角形)に注意しながら合同な三角形を見つけまくって角度を出すんだろうな」と思いました(結果的にチェバの定理は使いませんでしたが)。
案の定、それで正解でした。
\(BE\)と\(AE\)との交点を\(F\)と置きます。
このとき、メネラウスの定理から
$$
\frac{AF}{FC}\cdot\frac{3}{2}\cdot\frac{4}{3}=1
$$
が成り立ちます。

故に、
$$
\frac{AF}{FC}\cdot2=1\quad\Longleftrightarrow\quad FC=2AF
$$
となるため、\(AF:FC=1:2\)です。
ここで、\(\triangle ABF\)と\(\triangle CAD\)に着目すると、
$$
\angle A\equiv \angle C,\quad AF\equiv DC,\quad AB\equiv AC
$$
であるから、二辺夾角が合同なので、\(\triangle ABF\equiv\triangle CAD\)です。

従って、
\begin{eqnarray}
\angle BED&\equiv&\angle EAB+\angle EBA\\
&\equiv&\angle EAB+\angle EAC\equiv 60^\circ
\end{eqnarray}
と求まります。
ここでちょっと詰まりました。
グッと眼力を使うと、\(AF:FC=CD:DB=1:2\)なので、これを使えるんじゃないか?と思いました。
そこで、\(AB\)を\(2:1\)に内分する\(AB\)上の点\(G\)を取ることにしました。
そして、線分\(GC\)と線分\(BF\)との交点を\(H\)、線分\(AD\)との交点を\(I\)としました。
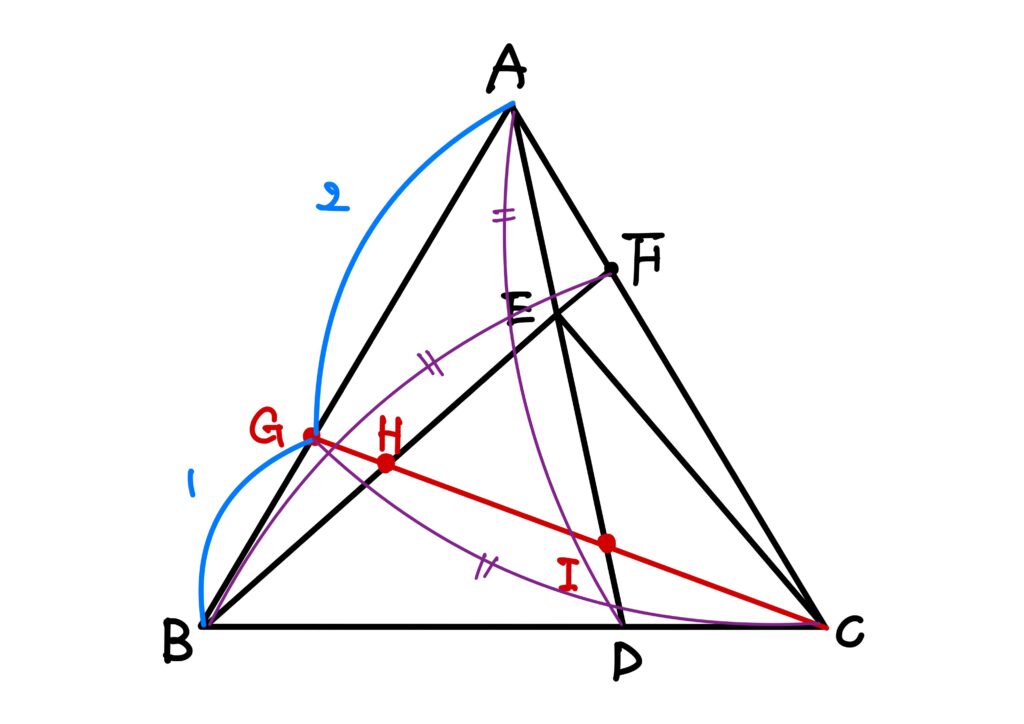
\(\triangle ABC\)は正三角形なので、\(AB\equiv BC\equiv CA\)です。
そして、\(AB\)を\(2:1\)に内分する点が\(G\)、\(BC\)を\(2:1\)に内分する点が\(D\)、\(CA\)を\(2:1\)に内分する点が\(F\)ですので、点\(G\)、\(D\)、\(F\)はそれぞれ\(AB\)、\(BC\)、\(CA\)を同じ比で内分しています。
従って、\(CG\equiv AD\equiv BF\)です。
さらに、\(AE:ED=3:4\)ですので、\(BH:HF=CI:IG=3:4\)です。
故に、\(AE\equiv BH\equiv CI\)です。
ということは、\(ED\equiv HF\equiv IG\)です。

ここで、\(\triangle ABD\)と\(\triangle BCF\)に着目してみます。
このとき、\(AB\equiv BC\)、\(\angle B\equiv \angle C\)であり、\(BD\equiv CF\)なので、二辺夾角合同により\(\triangle ABD\equiv \triangle BCF\)です。
従って、\(\angle EDB\left(\equiv\angle ADB \right)\equiv\angle HFC\left(\equiv BFC \right)\)です。
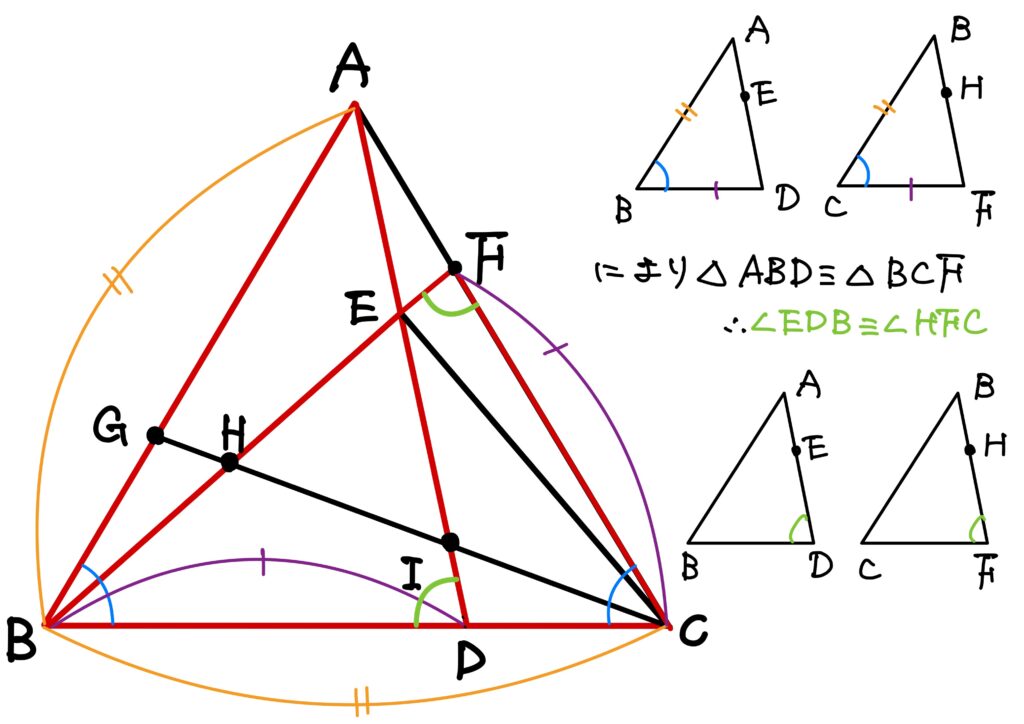
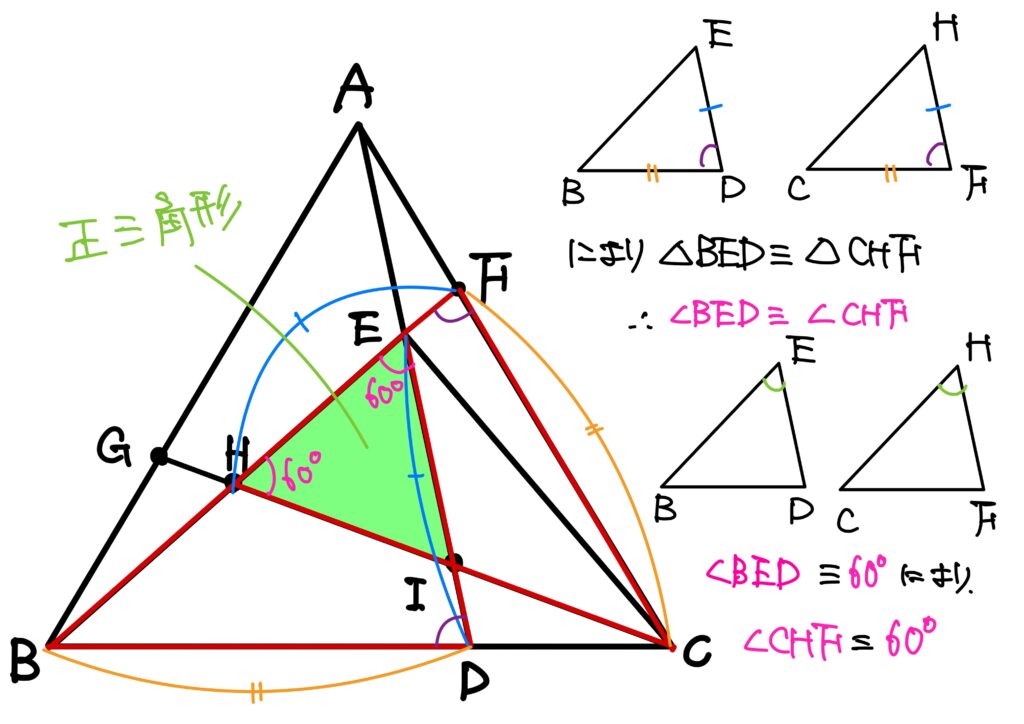
今、\(ED\equiv HF\)、\(\angle EDB\equiv \angle HFC\)、\(BD\equiv CF\)により、二角夾辺合同により\(\triangle EBD\equiv \triangle HCF\)です。
故に、\(\angle BED\equiv \angle CHF\)です。
\(\angle BED=60^\circ\)だったわけですので、\(\angle CHF=60^\circ\)です。
従って、\(\triangle EHI\)は正三角形であることが分かります。
さて、今度は四角形\(ABCI\)についてメネラウスの定理を使います。
\begin{eqnarray}
\frac{AG}{GB}\cdot\frac{BC}{CD}\cdot\frac{DI}{IA}=1&\Leftrightarrow&
\frac{2}{1}\cdot\frac{3}{1}\cdot\frac{DI}{IA}=1\\
&\Leftrightarrow&IA\equiv 6ID
\end{eqnarray}
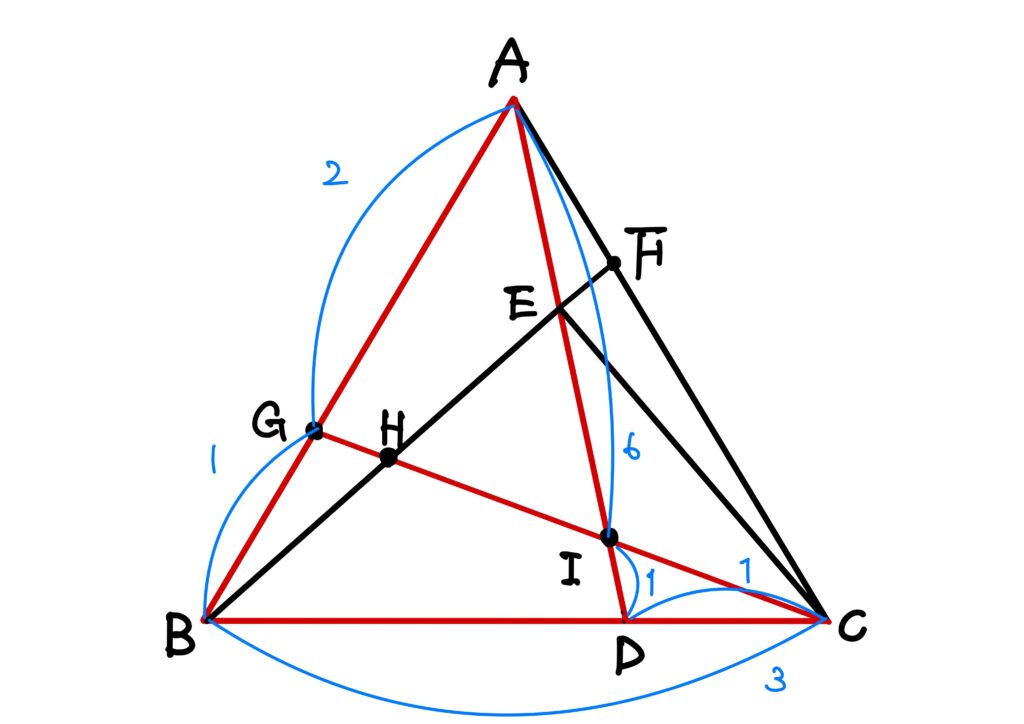
ここで、\(AE:ED=3:4\)で、\(AI:ID=6:1\)ですから、両者の比は計算にそのまま使えます。
故に\(AE\equiv 3ID\)であり、\(ED:ID=4:1\)ですので、\(ID\equiv 1\)とおけば\(EI\equiv3\)となるので、\(EI\equiv 3ID\)となります。
故に、\(AE\equiv IE\)です。
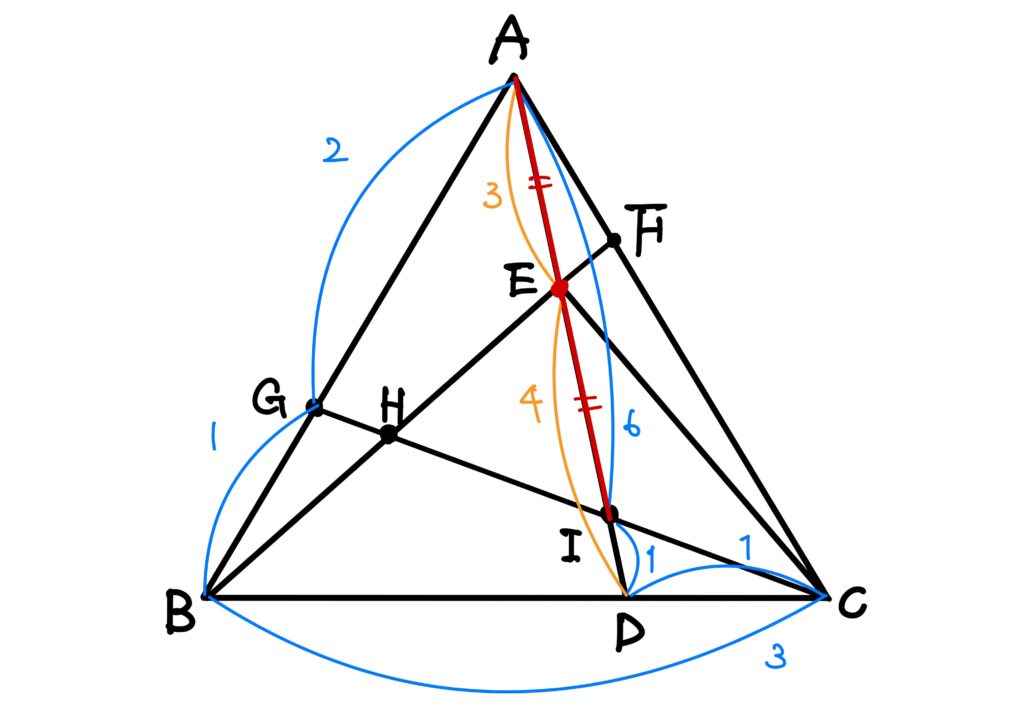
同様にして、\(BH\equiv HE\)、\(CI\equiv IH\)が求まります。
従って、\(\triangle EDC\)は二等辺三角形です。
\(\triangle EHI\)が正三角形だったわけですので、\(\angle EIC\)は\(\triangle EHI\)の外角だから、\(60^\circ+60^\circ=120^\circ\)、すなわち\(\angle EIC\equiv 120^\circ\)です。
故に、\(\angle IEC\left(\equiv\angle DEC \right)+\angle ICE\equiv60^\circ\)です。
そして、再度\(\triangle EDC\)が二等辺三角形であることを用いれば、\(\angle IEC\left(\equiv\angle DEC \right)\equiv\angle ICE\equiv30^\circ\)ということが分かります。
従って、\(\angle DEC\equiv 30^\circ\)です。

投稿されたエレガントな解答
では、エレガントな解答を紹介します。
(前略)
図を正確に書けば\(\angle BED=60^\circ\)、\(\angle CED=30^\circ\)の予想がつく。\(\angle BED=60^\circ\)ならば、\(\angle ABE=\angle DAC\)であるから\(BE\)と\(AC\)との交点を\(F\)として\(\triangle ABF\equiv\triangle CAD\)を示せば良いことに気がつく。
\(D\)を通って\(BF\)に平行な直線をひき、\(AC\)との交点を\(G\)とすれば
$$
AF:FG=AE:ED=3:4.
$$
また、
$$
FG:GC=BD:DC=2:1=4:2
$$
すなわち
$$
AF:FG:GC=3:4:2
$$
したがって
$$
AF:FC=3:(4+2)=1:2
$$
いま、\(AC=BC\)であるから
$$
AD=\frac{1}{3}AC=\frac{1}{3}BC=CD
$$
これと
$$
AB=AC,\quad \angle BAF=\angle ACD
$$
より
\begin{eqnarray}
&&\triangle ABF\equiv\triangle CAD\\
&&\therefore\quad \angle ABF=\angle CAD
\end{eqnarray}
よって
\begin{eqnarray}
\angle BED&=&\angle BAE+\angle ABE\\
&=&\angle BAE+\angle CAD=60^\circ\tag{1}
\end{eqnarray}
\(\angle FCD=60^\circ\)であるから、(1)より四角形\(EDCF\)は円に内接する。
したがって、
$$
\angle DEC=\angle DFC\tag{2}
$$
\(CF=2AF\)であるから\(CF\)の中点を\(M\)とすると\(CM=MF=AF=CD\)。これと\(\angle MCD=60^\circ\)から\(\triangle MCD\)は正三角形である。よって
$$
MD=MC=MF
$$
したがって
$$
\angle DFM=\angle FDM=\frac{1}{2}\angle DMC=30^\circ
$$
すなわち\(\angle DFC=30^\circ\)。これと(2)から
$$
\angle DEC=30^\circ。すなわち \angle CED=30^\circ
$$また\(\angle DFC=30^\circ\)をいうのに、\(A\)と\(BC\)の中点を結ぶ直線が\(FD\)に平行なことを比例で証明したもの、\(CF=2CD\)、\(\angle FCD=60^\circ\)から導いたものもあった。なお、\(AF:FC=1:2\)の証明にメネラウスの定理を用いたものもあった。
\(AB\)上に\(X\)を\(AX:XB=2:1\)にとり、\(CX\)と\(BF\)、\(AD\)の交点を\(Y,Z\)とすると
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p84-86.
$$
CZ:ZY:YX=3:3:1
$$
であることがわかる。\(\triangle EYZ\)が正三角形になることと\(YZ=ZC\)から\(\angle DEC=30^\circ\)を示すことができる。
また\(\triangle ABC\)の外接円と\(AD\)との交点を利用する解などもあった。
いやあ、中点を取るなんて思いつきませんでしたし、外接円を使うという発想もありませんでした。
すごいですね。
とはいえ、筆者は割と正攻法で解いたような気がしています。
読者の皆様への挑戦状!
今から紹介する問題の解答は来週解説します!
凸四角形\(ABCD\)の辺\(AB,\ BC,\ CD,\ DA\)上にそれぞれ点\(P,\ Q,\ R,\ S\)を
$$
AP=BQ=CR=DS
$$
であるようにとるとき、四角形\(PQRS\)が正方形ならば、もとの四角形\(ABCD\)も正方形であることを証明して下さい。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13-14.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
今回の問題は図形の問題で、比較的簡単な部類に入るかと思います。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!






コメントをする