本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
※「これを5分で解けるかな!?」も是非挑戦してみて下さい!
前回の問題については以下の記事を御覧ください!
今日の問題
ウィンブルドンのテニスや甲子園の高校野球など、勝ち抜きトーナメント形式で優勝者を決める方式は、参加者数に比べて総試合数が少なくてすむ利点があります。すなわち、参加者が\(n\)なら総試合数は\(n-1\)となります。もし総当たりリーグ戦にすれば、\(\displaystyle\frac{n(n-1)}{2}\)試合が必要ですから、\(n\)が大きい場合に総試合数の差がはっきりします。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p28.
勝ち抜きトーナメントの欠点は、半数の参加者が1試合だけで姿を消してしまうことです。そこで、1敗で失格という規則を少しだけ緩和して、2敗で失格という規則を考えます。このとき、総試合数はいくつになるでしょうか。また、このときのエレガントな組合せ方式を求めてください。毎回残っている参加者が抽選で対戦相手を決めるような方式でなく、おおよその対戦表が予め決まっている方式を考えて下さい。
チャレンジの結果…
チャレンジの結果…解けました。
ただ、エレガントかどうかというのは意見が分かれると思います。
筆者が思うエレガントな解答を定め、その上で挑みました。
筆者の解答
解答を出すまでは1時間もかかりませんでした。
試合数については直ちに分かりました。
まず、通常の勝ち抜き戦の試合数は、エントリー数が\(n\)の場合、\(n-1\)回です。
2敗の場合は、優勝者が全勝のときは\(2(n-1)=2n-2\)回で、優勝者が1敗のときは\(2n-2+1=2n-1\)回と分かります。
後は、2敗で脱落という条件を満たす勝ち抜き戦を定めればOKですが、”エレガント”な解答を求められています。
筆者は本問題におけるエレガントな解答を「選手が分かりやすい単純な試合形式であり、かつ大会時間が短いもの」と定めました。
というのも、「ああ、そういう発想もあるか!」となる解答も確かに良いと思うのですが、実際試合をするのはあくまで選手であって、いくら斬新な発想だったとしても複雑であれば試合運営に支障をきたすだろうと思うからです。
さらに、いくらシンプルだからといって何時間もかかるような大会形式は望ましくないと考えます(実際には競技によって同じ形式を採用しても大会時間が異なるのでしょうけれども)。
そういう意味で、シンプルな解答を筆者はエレガントと思って考えました。
最もシンプルだと思われるのは、勝ち抜き戦を2回独立で行うことだと考えました。
各勝ち抜き戦で優勝者が一致している場合はその選手が優勝です。
一方で、一致していない場合は決勝戦を行います。
この場合、試合数はたしかに\(2n-2\)回か\(2n-1\)回です。
実際、各勝ち抜き戦の優勝者が一致している場合は、各勝ち抜き戦での試合数が\(n-1\)回であり、それが2回行われるわけですから\(2(n-1)=2n-2\)回です。
一方で各勝ち抜き戦で優勝者が一致していない場合は、各勝ち抜き戦終了時点で\(2n-2\)回の試合数があり、1敗の選手が2名います。
そして、最終的に決勝戦を行うため、\(2n-2+2=2n-1\)回の試合数となるわけです。
これだと確かにシンプルで分かりやすい一方で、時間がかかりすぎるのが欠点だと思います。
さて、どうしたものでしょうか。なるべく時間を短くしたいのです。
ここで、筆者の経験を思い出してみました。
以前述べたかもしれませんが、筆者は小学校1年から高校3年まで剣道をやっていました。
剣道の試合は基本的にトーナメントですが、トーナメントをブロックに分けて6つのコートで同時並行して行います。
ということで、単純に「複数のコートで同時並行して行えば?」という発想に至りました。
そこで、次の試合形式を思いつきました(これも単純なもの)。
- コートを2つに分ける。
※第\(k\)コート第\(l\)試合を第\((k,l)\)試合と書くことにします。 - 第\((1,1)\)試合はコート1のみを使い行う。
- 第\((1,1)\)試合終了後、勝者はそのコートに残り、敗者は第2コートに移動。
- 第\((1,2)\)試合は1コートで行い、その勝者がまた第1コートに残り、敗者は第2コートへ移動。
- 第\((2,1)\)試合は、第\((1,1)\)試合の敗者と第\((1,2)\)試合の敗者で勝ち抜き戦を行う。
これと同時に\((1,3)\)試合を行う。 - この形式を繰り返す。
- 第2コートでの敗者は失格とする。
この形式は、第1コートと第2コートの試合のタイミングが2試合分ずれるだけで試合数は\(2n-2\)か\(2n-1\)かのいずれかです。
しかも、単純に2回の勝ち抜き戦をやるという形式よりも時間が約半分になります。
というのが、筆者の解答です。
余談(読み飛ばしてOK)
正直なところ、筆者はそもそも勝ち抜き戦をあまり好んではいません。なぜなら、順番が後であればあるほど試合数が少なくて済むため、疲れなどの関係から順番が後ろの選手が有利だと感じるからです。
残りの体力を加味するとフェアな対戦とは言えないのでは?と思うわけです。
投稿されたエレガントな解答
(前略)
まず総試合数は、優勝者が全勝か1敗かに応じて、\(2n-1\)かまたは\(2n-1\)のいずれかになることが、容易に分かる。ひとりを残して\(n-1\)人が2敗になるためには、それだけの試合数が必要かつ十分である。そこで問題は、エレガントな対戦方式の組みかたである。
(中略)の分類によれば、エレガントさの判断基準は次のように整理できる。すべての項目に満点がつくことはむずかしいにしても、できるだけ多くの項目を満たすことが望ましい。(A)各選手の優勝までの所要試合数をできるだけ等しくすること。
(B)同一対戦の反復をできるだけ避けること。
(C)競技開始時点で対戦組合せが確定している部分が多いこと。
(D)対戦組合せの方式が一貫した原理に基づいていること。
(E)対戦組合せの方式を感銘に図示あるいは記述できること。実は出題者は、オリンピック精神のように、「勝つことよりも参加すること」を尊ぶような美的感覚をエレガントさに含めたいと考えていた。言い換えれば、ひたすら優勝を目指して競技することではなく、競技を楽しんでいる中で誰かがたまたま優勝者となる、といった対戦方式を出題者はエレガントだと思いこんでいたことになる。しかし、出題文中からはそれを読み取れなかったかもしれない。アンフェアだ、という声が聞こえてくる気がする。それにしても、勝敗のみにこだわる昨今の風潮はいかがなものであろうか。
さて、考えられる対戦方式を大きく分類すると、次のように成る。
(1)毎回、まだ2敗していない先週の間で抽選をして対戦相手を決める。二杯になったら脱落し、最後まで勝ち残った選手が優勝となる。
これは、出題文中で排除した方式で、(A)-(E)の多くも満たしていない。もちろん、この方式でも、同一対戦の重複を避ける工夫や、不戦勝の回数をできるだけ均一にする工夫などを取り入れて、全くランダムではない抽選にすることは可能である。
(2)通常の勝ち抜きトーナメントを独立に2度おこな手、それぞれの優勝者が別人の場合には、ふたりで決勝を行う。
これは、大相撲のトーナメントなどで実施している方式である。ここでも、たとえば1日目に貴乃花と武蔵丸、曙と若乃花が準決勝で当たるようにシードしてあったら、2日目は貴乃花と若乃花、曙と武蔵丸が準決勝で当たるようにシードするなど、有力選手のシードを工夫することで、同一対戦の重複を避けることができる。
(3)通常の勝ち抜きトーナメントを行いながら、並行して敗者復活戦を行い、1敗者の中から最後にひとり勝ち残った選手が全勝の選手と決勝を行う。
ただし、敗者復活側の選手は決勝で2連勝しないと優勝できない。
おそらくこの方式を考える解答が多いだろうと想像したが、やはり予想どおり、応募解の大多数はこの敗者復活方式をいかに工夫するかというものだった。1回戦敗退組の代表、2回戦敗退組の代表、等々を集めたトーナメントを行う方法、そのトーナメントに勝ち残った全照射も含める方法、1回戦敗退組のトーナメントに2回戦敗退組を織り込み、そこに2回戦敗退者を織り込む等々という方式をとる方法など、いくつもの変種がある。最後にふれた織り込み型の方法では、同一対戦の重複をなるべく避けるために、隣の山で2回戦敗退した選手を1回戦敗退組初戦の商社に当てるなどの工夫ができる。
何かものの本で呼んだ記憶では、昔甲子園の高校野球には敗者復活制をとりいいれたところ、敗者復活から優勝したティームが現れて、やっぱりそれはやめようということになったそうである。柔道の国際試合では、決勝に勝ち残った選手に破れた場合のみ、部分的な敗者復活線を行って、銅メダルの機会を与えている。また囲碁の十段戦でも、敗者復活戦を用いた組合せを使っているが、最後の決勝戦は1試合のみで、全勝で決勝に臨んで敗退すると1敗で失格になり、2敗失格制とは異なるそうである。
(4)通常のリーグ戦のつもりで試合を行いながら、2敗した選手を含む試合はスキップしていく方法。
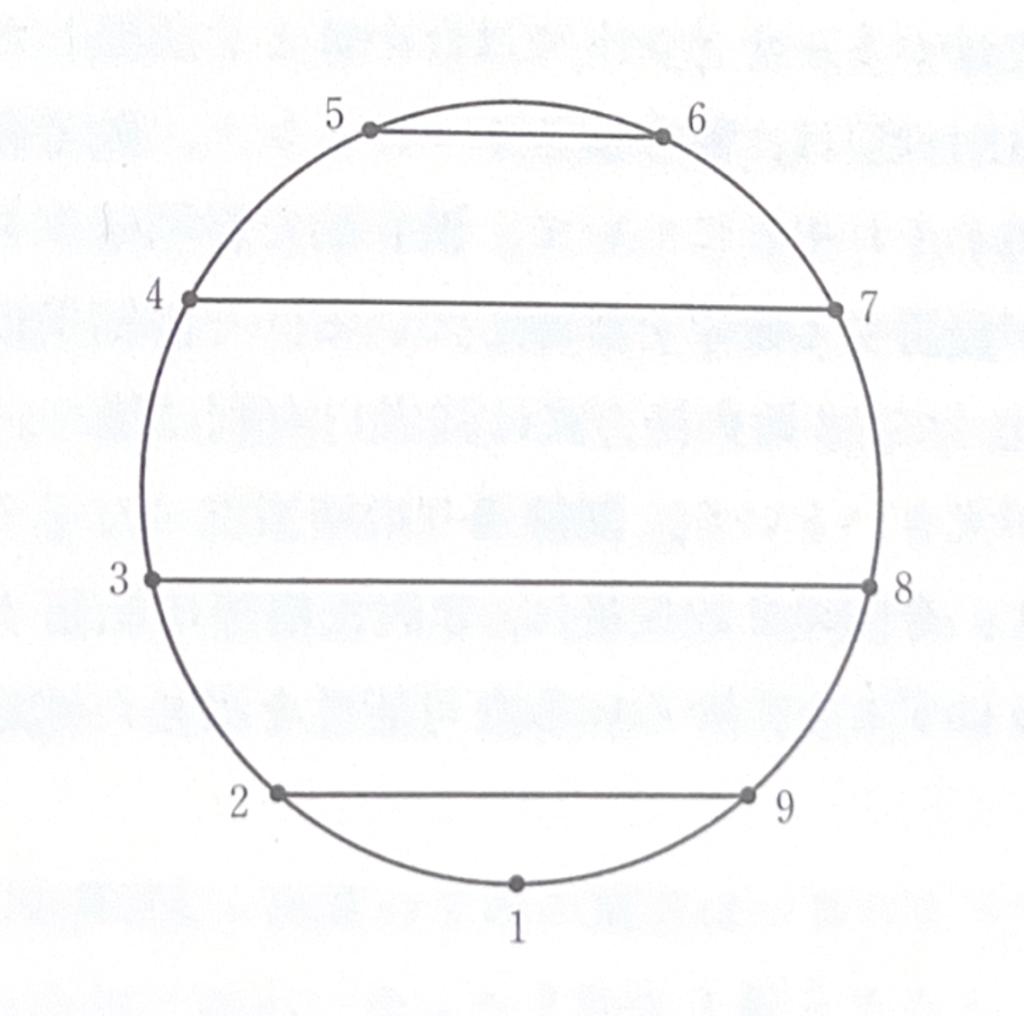
筆者が期待していた解はこれである。一般に\(m\)が奇数のときのリーグ戦の組合せは、円周を\(m\)等分した頂点に\(1\)から\(m\)までの番号をふり、長さが\(1/m\)の孤を張る弦、長さが\(2/m\)の孤を張る弦、等々を書き込んだ図を利用して作る。番号が選手の識別子で、弦が対戦を表す。弦がない頂点は対戦休みである。弦のパターンを円周に沿って\(1/m\)だけずらすことによって、2回戦の組合せになり、以下同様である。また\(m\)が偶数のときは、ここの対戦で\(m+1\)番目の選手を導入し、先程の対戦休みとした人を相手に組めば良い。(円周を偶数等分したのではうまくいかないことに注意)2敗方式の対戦でも、こうして作ったリーグ戦の対戦表を利用してもいいが、より優れた方法がある。最初の2番目の試合は、選手を円周上に並べて両隣と対戦させ、そこで2歯医者を除いて円周をすぼめ、隣同士の顔ぶれが変わるように局所的に隣同士の入替えをしてから、再び隣同士の対戦を行って、2敗者を除くことを続ける。ここでも、対戦休みの回数をできるだけ均一にする工夫を含めることができる。ただし、この微調整で同一対戦の重複を避ける部分は、さきほどの基準(D)と(E)からみて、あまりすっきりとはしていない。
最初の2試合を円周の隣同士で行うやり方は、古きよき旧制高校時代の9人制バレーボール大会で採用していたそうである。この方法では、ときには全選手が1勝1敗になる可能性もあり、勝ち抜きトーナメントのようなピラミッドをひたすら登るようなイメージではないところが、筆者の美的感覚にマッチしている。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p241-p244.
筆者の解答も(3)に該当するものでしょう。
(4)のリーグ戦形式にする、という発想はありませんでした。
!次回予告!
立方体の6面を絵の具で塗り分けます。使える色は6色までで、すべて違う色でも、2色か3色だけを使っても、まったく自由です。違う塗り方は全部で何通りありますか。ただし、立方体を転がしたとき同じ塗り方に成るものは1通りと数えます。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p28.
立方体の特徴をうまくみつけると、群論などの知識を使わなくても、ごく簡単に答えは出ます。
次回は、この問題に挑戦します!
前回の問題は【1時間チャレンジシリーズ】挑戦㊱を御覧ください!
筆者からの挑戦状!(5分で解けるかな!?)
サクッと挑戦できる問題を筆者が考えて出題したいと思います!
5分程度で解ける問題を出していきたいと思います。
\(\log_{10}2=0.3010\)、\(\log_{10}3=0.4771\)のとき、\(5^{55}\)の最高位の自然数を求めよ。
高校数学の問題ですね。
案外ぱっと解けないこともある高校数学ですが、これはどうでしょう?
ちなみに、基準として筆者は2分30秒くらいでした。
解けた方は、本記事へコメントするか、Twitter、instagramのDMで解答を送って下さい!
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「筆者からのの挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!




コメントをする