本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題を1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。
前回の問題については以下の記事を御覧ください!
問題を明示します。
シルクロードの遺跡を発掘していた数セミ隊は、ネストリウス派の教会跡と思われるところから青銅の箱に収められた文書を発見した。それはソグド文字で記載される交易に関する文書群であった。それによれば、この遺跡の周辺にはなお5つの都市が存在していたことが解る。現在発掘中の都市を\(A_1\)とする。この他に\(A_2,A_3,B_1,B_2,B_3\)という都市が存在した。文書によれば、都市\(A_i\)から\(B_j\)へは\(i+j\)日かかるという。また、ある断簡によれば、\(A_x\)から\(B_y\)へ向かうカラバンと\(B_w\)から\(A_z\)に向かうキャラバンとが、その道筋で出会ったときに何か争いを起こしたと思われるが、\(x\neq z\)、\(y\neq w\)であるらしいことは解るものの、\(x,y,z,w\)そのものは読みとれない。
各都市の間の道は直線的であったとし、かつその間を移動するのにかかる日数はちょうど距離に比例すると仮定して、その位置関係を探って今後の発掘の参考にしたい。
- いま簡単のために\(x=1\)、\(y=2\)、\(z=2\)、\(w=1\)を仮定してその位置関係を考えて見たところ、この仮定の下ではなんと\(A_1\)、\(A_2\)、\(B_1\)、\(B_2\)は一直線上に存在することが解った。
- 上記の仮定を置かずにさらにいろいろと考えたところ、実はすべての6つの都市が一直線上にあることが解った。
さて、上記のことを確認していただきたい。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p19-p20.
前回の問題は【1時間チャレンジシリーズ】挑戦㉓を御覧ください。
チャレンジの結果は…?
チャレンジの結果….半分だけ解けました…
1.は特に問題はなく解けたのですが、2.については条件に混乱してタイムアップでした。
筆者の解答を紹介します。
まず、この問題を見た瞬間に「お?これはグラフ理論の問題かな?」と思いました。
しかし、距離が関わってくるということで真正直なグラフ理論の問題ではないようでしたが、結局の所は平面図形の問題(とりわけ単に三角形の辺の長さの関係式の問題)ということが見えてきました。
さて、解答です。
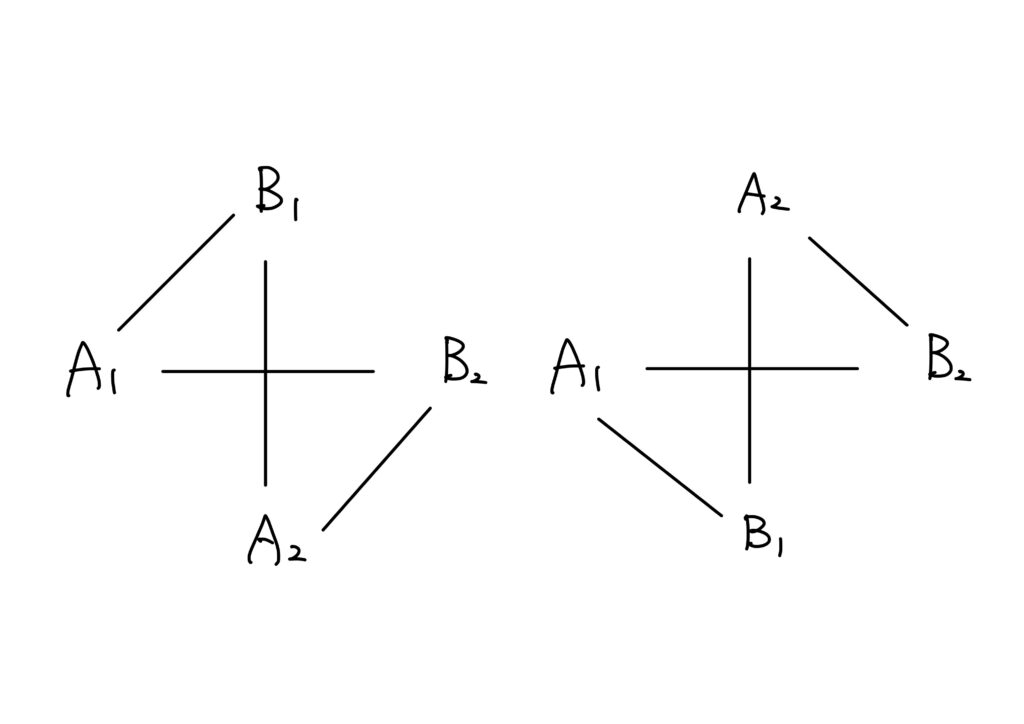
\(A_1\)から\(B_2\)に向かうカラバンと\(B_1\)から\(A_2\)に向かうカラバンが本当に争ったのかは別として、少なくとも出会ってはいます。
故に、都市\(A_1\)から\(B_2\)に向かう道筋(今回は直線ですが)と都市\(B_1\)から\(A_2\)に向かう道筋は交わっている、ということになります。
この交点を\(P\)と書くことにします。
これを図で表すと以下のようになります。
これをさらに図形的にシンプルにすれば、以下のようになります。
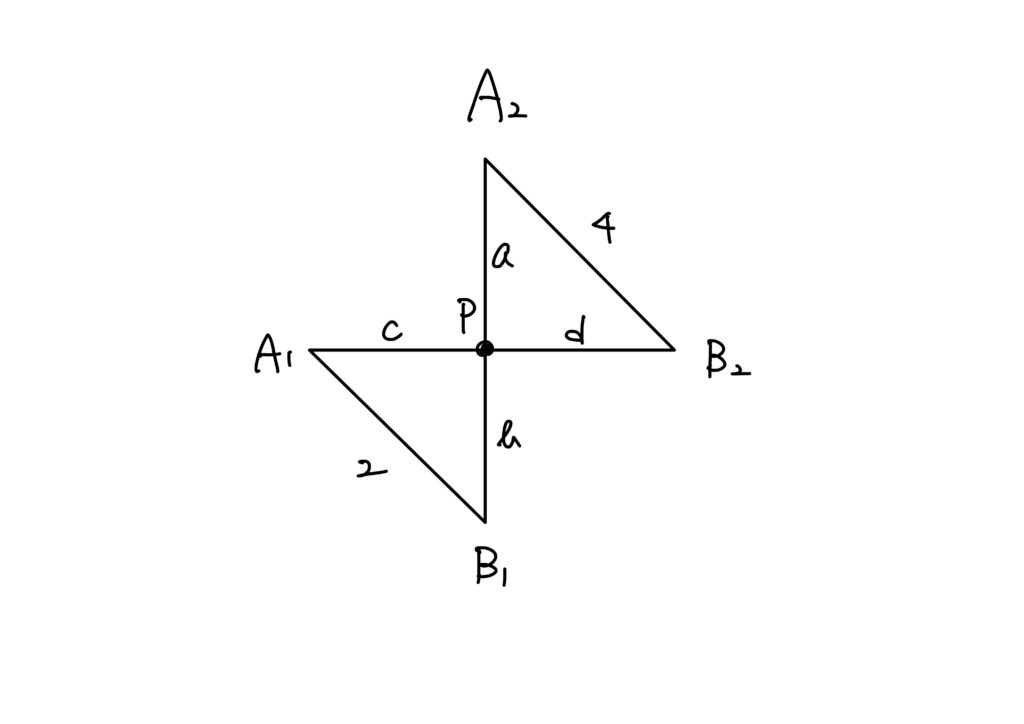
ここで、
$$
A_2P=a,\quad PB_1=b,\quad A_1P=c,\quad PB_2=d
$$
とします。
すると、\(A_i\)から\(B_j\)までは\(i+j\)日かかるわけですので、\(a+b=3\)です。
同様にして、\(c+d=3\)となります。
さて、\(A_1\)、\(A_2\)、\(B_1\)、\(B_2\)が同一直線上に存在しないとしてみます。
すると、都市\(A_2\)、\(B_2\)と地点\(P\)は三角形をなしていることになります。
三角形の辺の長さの関係から、三角形の3辺のうち、2辺の長さの和は他の1辺の長さより大きいです(さもなくば三角形になりません)。
故に、
$$
a+d\geq 4
$$
が成り立ちます。
同様にして
$$
c+b\geq \geq2
$$
となります。
これらの不等式の和を取れば、
$$
a+b+c+d\geq6
$$
が成り立ちます。
\(a+b=3\)、\(c+d=3\)だったわけですので、\(a+b+c+d=6\)ということになります。
ということは、\(a+d=4\)、\(b+c=2\)でなければなりません。
以上のことから、
\begin{eqnarray}
&&A_2P+PB_2=A_2B_2\\
&&A_1P+PB_1=A_1B_1
\end{eqnarray}
となるため、\(A_1\)、\(A_2\)、\(B_1\)、\(B_2\)は同一直線上にある、ということになります。
ここでふと「これ、一般化できるんじゃないか?」と思いましたので、やってみました。
\(x\neq z\)かつ\(y\neq w\)を満たすような\(x,y,z,w\)に対して、\(A_x\)、\(A_z\)、\(B_y\)、\(B_w\)が同一直線上にあることを示してみます。
この場合は先程と同様に、以下のような状況になります。
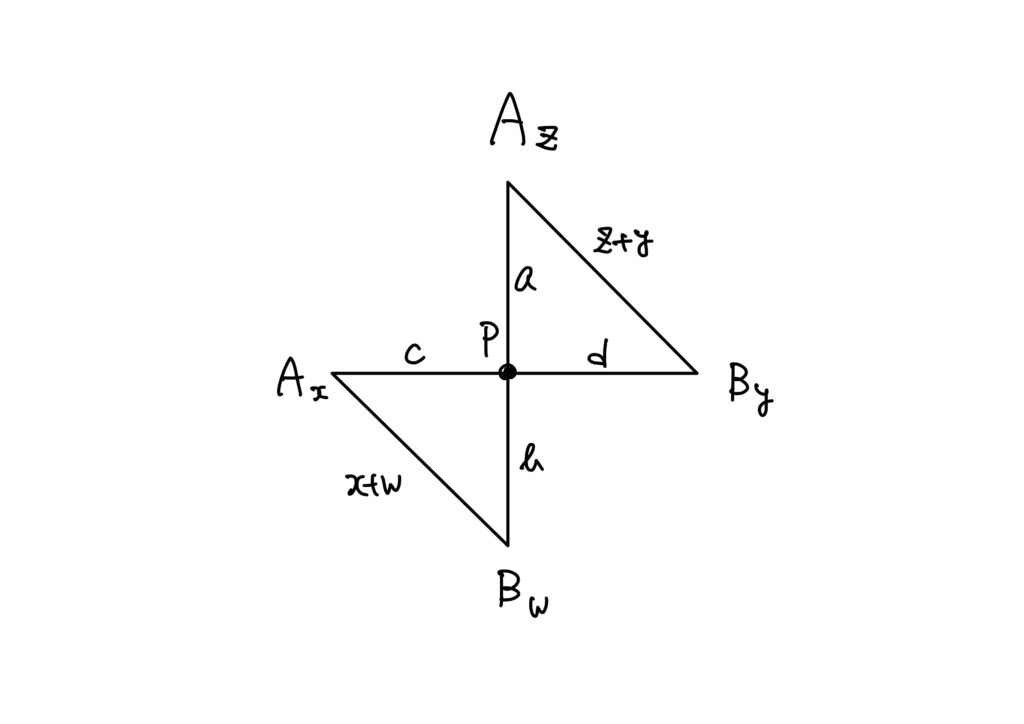
先程と同様にして、
$$
a+b=x+y,\quad c+d=z+w
$$
を得ます。
再度三角形の辺の長さの関係から、
$$
a+d\geq x+y,\quad c+d=z+w
$$
となるため、
$$
a+b+c+d\geq x+y+z+w=a+b+c+d
$$
により、
$$
a+d=x+w,\quad b+c=z+y
$$
となるから、一直線上に存在します。
続いて、2.です。
冒頭で述べた通り、解けませんでした。
都市が6つの場合、先程の議論から、都市\(A\)が2つ、都市\(B\)が2つの4都市は同一直線上にあることが分かりました。
あと都市\(A\)1つ、都市\(B\)1つの系2つも同一直線上に存在するということを示せばOKです。
この2つの都市をそれぞれ\(A_s\)、\(B_t\)と書くことにします。
同一直線上に存在する都市を\(A_x\)、\(A_z\)、\(B_y\)、\(B_w\)と書いたとします。
このとき、位置関係は以下のようになります。
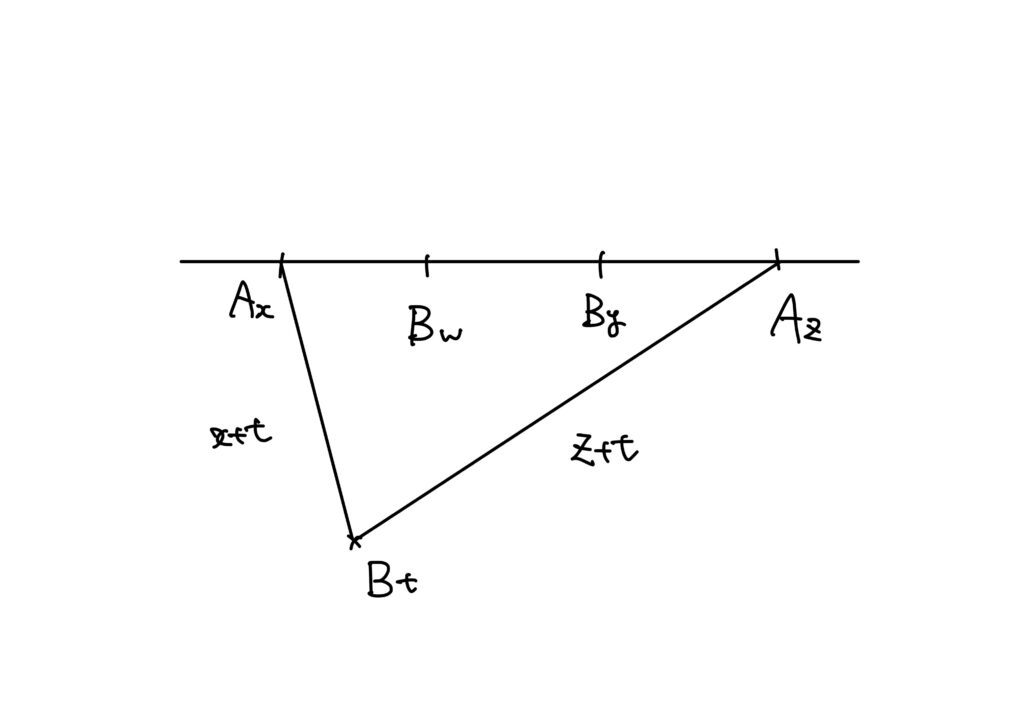
しかし、\(A_x\)と\(A_z\)の距離と\(B_y\)と\(B_w\)の距離を求めることができず、タイムアップでした。
残念です…
投稿されたエレガントな解答を紹介します!
筆者の解答と似ている部分は省略します。
(前略)
三角不等式 さて、この問題は実は三角不等式のみですべての照明ができます。つまり、次の主張のみを用います。\(\triangle ABC\)の角\(A,B,C\)の対辺を\(a,b,c\)とするとき、
\(a+b\geq c\)であり、ここで等号は三角形が線分(\(A\)、\(B\)、\(C\)の順)
に退化するときに限る。
また三角不等式を次の形で利用された方もあります。
ベクトル\(\alpha\ (\alpha\neq0)\)、\(\beta\)が\(\left\|\alpha\right\|+\left\|\beta\right\|=\left\|\alpha-\beta\right\|\)をみたせば、
\(\exists r\leq0\)、\(\beta=r\alpha\)。(中略)
\(A_xB_y\)と\(A_zB_w\)が交わるので、交点を\(Q\)とする。
(中略)
個々の4都市の順序は\(x,y,z,w\)の値に関係して決まりますが、三角形の退化の状況から解るように、\(A_\ast\)が2個と\(B_\ast\)が個、というように纏まっています。よって、\(A_x\)、\(A_z\)、\(B_w\)、\(B_y\)という順序で一直線上にあるとしてみましょう。すると、条件では与えられていない距離が分かります。すなわち、
\begin{eqnarray}
&&\overline{A_xA_z}=(x+w)-(z+w)=x-z,\\ \tag{4}
&&\overline{B_yB_w}=(z+y)-(z+w)=y-w,
\end{eqnarray}
であり、特に\(x\geq z\)、\(y\geq w\)となります。6都市の場合
前節の議論は、ある4都市(\(A\)2つと\(B\)2つ)は一直線上に存在する、というものです。\(x,y,z,w\)が任意の値というのではありませんから6都市が一直線上というためには残る2都市\(A_u\)、\(B_v\)もその直線上にあると言わねばなりません。この点を勘違いされた方がありました。また、\((x,y,z,w)=(1,2,2,1)\)の場合には\(A_1B_2\)と\(A_2B_1\)が交わると言っているのみであって、\(A_1B_1\)と\(A_2B_2\)が交わるかどうかについては何も言っていません。これも誤解をされた方があります。
それでは、\(B_v\)から\(A_x,A_z\)へのよりを考えてみましょう(図2).問題の条件から(5)を、三角不等式と(4)第1式と(5)から(6)を得ます。
\begin{eqnarray}
&&\overline{A_xB_v}=x+v,\quad \overline{A_zB_v}=z+v,\tag{5}\\
&&x+v=\overline{A_zB_v}+\overline{A_xA_z}\geq \overline{A_xB_v}=x+v\tag{6}
\end{eqnarray}
(6)によれば、\(\triangle A_xA_zB_v\)は線分に退化しており、よって\(B_v\)もまた直線上に乗りました。\(A_u\)に関しても、同様に\(A_uB_wB_y\)を得て、直線上にのります。
これで、6都市が一直線上にあることが、三角不等式のみを用いて証明できました。最終的な配列は\(A_3,A_2,A_1,B_1,B_2,B_3\)の順です。その他の方法
\(\triangle A_xB_wQ\)と\(\triangle A_zB_yQ\)に余弦定理を適用し、
$$
\frac{a^2+d^2-(x+w)^2}{2ad}=\frac{(x+y-a)^2+(x+w-d)^2-(y+z)^2}{2(x+y-a)(z+w-d)}
$$
を変形して因子に\((x+w-a-d)\)をだし、\(x+w=a+d\)を導く方法もありますが、もう一つの因子が\(0\)でないことの保証は面倒です。
多少毛色が違うのは(中略)氏によるものです。そこでは、次の順序で背理法によって証明します。この場合は距離の条件と\(A\)または\(B\)が3点存在することのみから導かれ、例の「カラバンが出会う」条件は必要ありません。これもたしかにエレガントな方法です。
- ある3点\(A_x\)、\(A_z\)、\(B_y\)が一直線上にあれば、その他すべての\(A_\ast\)、\(B_\ast\)もその直線上にある。
- ある3点\(A_x\)、\(A_z\)、\(B_y\)が一直線上になければ、その他の\(B_\ast\)は半直線\(A_xB_y\)と\(A_zB_y\)で挟まれる部分とそれの\(A_xA_z\)で線対称な部分にある。
- いかなる3点\(A_x\)、\(A_z\)、\(B_y\)も一直線所うになければ、他の\(B_\ast\)の存在する範囲がなくなり、矛盾する。(実際には\(A_x\)、\(A_z\)、\(A_w\)、\(B_y\)を取り、前項の範囲の共通部分を考える)
すべてを座標で実行する方法や、円や双曲線を用いる方法も面白いのですが、説明がいろいろ面倒になり多少紙数を取るので残念ながら割愛します。
円を用いいる方法で一見要領のいいのは、今\(x+y\geq z+w\)と仮定して、\(A_x:(-x,0)\)、\(B_y:(y,0)\)と座標をとります。中心\(A_x\)、半径\(x+w\)の円\(C_b\)は\(B^\prime:(w,0)\)を通り、中心\(B_y\)、半径\(y+z\)の円\(C_a\)は\(A^\prime:(-z,0)\)を通ります。したがって、\(\overline{A^\prime B^\prime}=z+w\)を直径とする円\(C\)が、\(C_a\)、\(C_b\)に接しています。\(A_z\)は\(C_a\)上に、\(B_w\)は\(C_b\)上に存在し、\(\overline{A_zB_w}\)は\(\overline{A_xB_y}\)と交わりかつ長さが\(z+w\)とならねばなりません。これらの条件を満たしているのは\(A_z=A^\prime\)、\(B_w=B^\prime\)でなければならない、と結論します。しかし、図を示すだけでは明らかでなく、結局論証を必要とします。(後略)
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p162-p165.
読者の皆様への挑戦状!ぜひ解いてみて下さい!
以下の問題は来週挑戦します!
\(10\)と互いに素な全ての自然数は、\(11\cdots1\)のように、\(1\)を並べた倍数を必ず持つことを示してください。
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p21.
例 \(3\times37=111\)
\(7\times15873=111111\)
\(9\times12345679=1111111111\)
\(11\times1=11\)
\(13\times8547=111111\)
前回の問題は【1時間チャレンジシリーズ】挑戦㉓を御覧ください。
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!
他の「エレガントな解答をもとむ」の問題に挑戦してみたい方はぜひ以下の書籍をお買い求め下さい!





コメントをする