(数セミ)”エレガントな解答をもとむ”に1時間で挑戦！読者の皆様への挑戦もあります！【挑戦⑬】

本記事の内容

本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。

本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。

今回も「エレガントな解答をもとむ selections」に掲載されいている問題です。

前回の問題については以下の記事を御覧ください！

(数セミ)"エレガントな解答をもとむ"に1時間で挑戦！読者の皆様への挑戦もあります！【挑戦⑫】

...

for-spring.com

2022.10.15

では、問題

一郎君は、軸と軸受が同心円でないのに、ベアリングを入れようと考えました。ヤマカンで選んだ場所から出発して順次、軸と軸受と直前のベアリングに接するようにベアリングの球の大きさを変えながら入れていくと、なんと最後のベアリングが最初のベアリングにちゃんと接しました。ラッキー！

しかし、このような幸運に恵まれたときは、実はどこからベアリングを入れ始めてもちゃんとベアリングの輪は完結するのです。これを証明して下さい。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p15.

いざ、チャレンジ

チャレンジの結果…解けませんでした。
この問題はどこかで見たことがあるような気がしましたが、結局関係ありませんでした。
一応何か分かるかも知れないと思い、手を動かしてみましたが、ほぼ手も足も出ないような状況でした。
悔しい…

色々手を動かしてみましたが、結局意味のないことでしたので、筆者の回答は省略します…ごめんなさい。

投稿されたエレガントな解答

　出来の悪い数学科学生だった私は、当然、複素関数論などもチンプンカンプンだったわけです。 そういう私でもハット驚いた問題がこれでした。 複素関数論？ そう、この問題を得には結構たいそうな飛び道具を使うのです。 と、おもっていたら、寄せられた解答で私の不明を正してくださった方が多数いらっしゃいました。
　実はこの問題は昔から有名な問題で、あちこちの本に紹介されているようです。 あとで述べますが、私が知っていた複素関数論の一次変換を使う証明は（中略）さんからのご教示によれば、1906年にケーべ(P. Koebe)が行ったのが最初とのことです。 しかし、実は1928年に、エレガントな幾何学的証明がシュタイナー(J. Steiner)によって行われており、そのためのにこの問題はシュタイナーの定理とも呼ばれているそうです。
（中略）

これでもまだ話は終わらず、4\triangleleftのアレキサンドリアの数学者パップス(またはパッポス)が登場します。 彼は「靴屋のナイフ」と呼ばれる図形(図1で円$O_1$、$O_2$、$O_3$の半周によって囲まれた領域)の内部に順に内接していく円の列$P_1,P_2,P_3,\cdots$の直径$d_1,d_2,d_3,\cdots$と、これらの円の中心から円$O_1$の直径$AB$へ引いた垂線の長さを$h_1,h_2,h_3,\cdots$に関して非常に見事な関係式が成り立つことを発見しました(パップスの定理)。 $$h_1=d_1,\quad h_2=2d_2,\quad h_3=3d_3,\quad\cdots,\quad h_n=nd_n,\quad \cdots$$ 　そして、シュタイナーの定理はパップスの定理を証明するための1つの系だったというのです。 だから、シュタイナーの定理は本来、パップス-シュタイナーの定理と呼ぶべきかもしれません。 もっともパップスの証明はあまりエレガントではなかったようです。

　さて、問題の解答に移りましょう。 反転法にしろ、一次変換にしろ、予備知識が必要ですが、それらはふつうの教科書には出ていますので、基本的な事実は証明なしで説明させていただきます。 また、証明を完全なものにするための細かい計算も行いません。

[反転法による証明]　中心$O$、半径$r$の円$O$があったとき、点$O$と異なる点$P$について、半直線$OP$上に$OP\cdot OP^\prime=r^2$なる点$P^\prime$をとることを、$P$の円$O$による反転といいます(図2)。反転に関して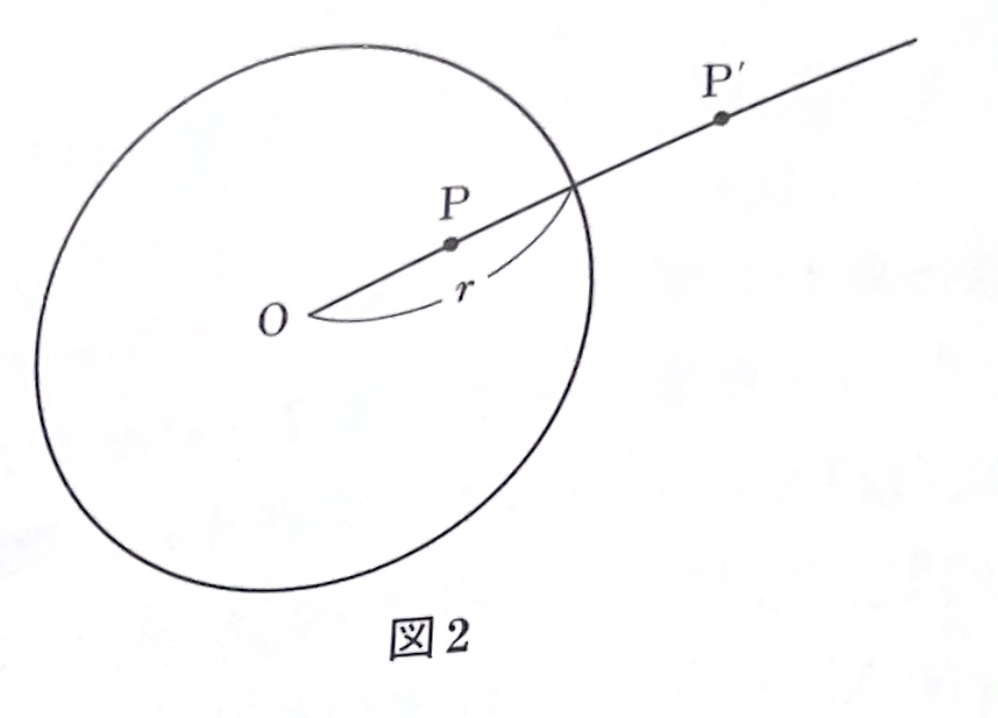

1. 反転により$O$を通らない直線と円は円に移る。$O$を通る直線と円は直線に移る。
2. 曲線(または直線)の広角は反転で不変である。
3. 互いに接する円ははんてんで映っても互いに接する。これは2.から明らか。

　次に、問題のように1つの円$O_1$の内部にすっぽり入ってしまい、かつ同心円でないときは、これを反転によって同心円に移せることが証明できます。 これには図3のように、2つの円に直行する円(と直線)が必ずある2定点$A,B$を通ることを利用します(これはピタゴラスの定理で簡単に証明できます)。 ここで点$A$を中心とする円 で円$O_1$と$O_2$を反転します。 すると、点$A,B$を通る円(と直線)はすべて$B$の反転$B^\prime$を通る直線になります。 上の事実2.により、これらは反転語の円$O_1^\prime$、$O_2^\prime$のどちらにも直交します。 つまり、円$O_1^\prime$、$O_2^\prime$のは同心円になるわけです(図4)。
　同心円でベアリングが完結すれば、どこからベアリングを入れても完結することは自明です。 これと上の事実1.と3.を使えば、もとの問題は容易に証明できます。

[一次変換を用いる証明]　では、複素関数論の飛び道具を使う証明を示しましょう。 複素平面で $$\frac{az+b}{cz+d}\quad (ad-bc\neq0)$$ という変換は円を円に移し、かつ曲線の広角を変えない等角写像です(直線も広義の円と考えます)。 つまり、上に述べた反転を少し一般化した変換になっています。 あとは反転法と同様、この返還によって2つの同心円に移せばいいわけです。 多少の計算が必要ですが、これは簡単に証明できます。 なお、この場合、反転法と違って、円の内外を反転させない変換が可能です。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p97-p101.

どうやら有名問題だったようです。
まさか複素関数論のお話が出てくるとは全く思いませんでした。
幾何学の問題を複素関数論の知識を使って解く、というように、一見関係なさそうな分野の知識を使って解くというのは数学をやる上での1つのロマンだと思います。

読者の皆様への挑戦状！

今から紹介する問題の解答は今週の日曜日に解説します！

円$O$の内部に円$O^\prime$があります。そして、$O$に内接し、$O^\prime$に外接する三角形$ABC$があるとします。(このような三角形を、$O-O^\prime$内接外接三角形と呼ぶことにしましょう。) このとき、円周$O$上の任意の一点$P$に対し、$P$を一頂点とする$O-O^\prime$内接外接三角形が存在することを示して下さい(図1)。さらに一般に、内接外接(星形)多角形についても同様のことが成立するかどうか調べてみて下さい(図2)。エレガントな解答を期待していますが、、えれー頑固な解答でも結構です。

数学セミナー編集部編（2001）『エレガントな解答をもとむ selections』日本評論社 p16

結

いかがでしたか？
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。

読者の皆様も是非一度挑戦してみて下さい！
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい！

質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

Twitterでもリプ、DM問わず質問、コメントを大募集しております！