本記事の内容
本記事は『数学セミナー』(日本評論社)に掲載されている”エレガントな解答をもとむ”に出題されいている問題に、1時間で解けるか、という挑戦をする記事です。
本記事を読むにあたり、前提知識は基本的に必要ありませんが、以前紹介した記事の内容を使う場合はその旨を記述することにします。
今回は「エレガントな解答をもとむ selections」に掲載されいている問題です。
では、問題
今回は前回の最後に「皆様への挑戦状」ということで提示した問題です。
図形の問題です。
凸四角形\(ABCD\)の辺\(AB,\ BC,\ CD,\ DA\)上にそれぞれ点\(P,\ Q,\ R,\ S\)を
$$
AP=BQ=CR=DS
$$
であるようにとるとき、四角形\(PQRS\)が正方形ならば、もとの四角形\(ABCD\)も正方形であることを証明して下さい。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p13-14.
いざ、チャレンジ
チャレンジの結果、解けました。
少々難しかったのですが、なんとか解けました。
筆者の解答
何を示せば良いかというと、
$$
\triangle APS\equiv \triangle BQP\equiv \triangle CRQ\equiv \triangle DSR
$$
かつ
$$
\angle A\equiv\angle B\equiv \angle C\equiv \angle D\equiv 90^\circ
$$
であることです。
直感的に、「\(\angle A\)、\(\angle B\)、\(\angle C\)、\(\angle D\)は\(90^\circ\)だろうな」と思ったので、それぞれが\(90^\circ\)でないとして矛盾を導きつつ、なんとか直角三角形を作ってそれらが合同であることを示す、ということにしました。
\(\angle B>90^\circ\)かつ\(\angle C<90^\circ\)として、\(P\)と\(R\)から直線\(BC\)に下ろした垂線との交点をそれぞれ\(T\)と\(U\)とします。
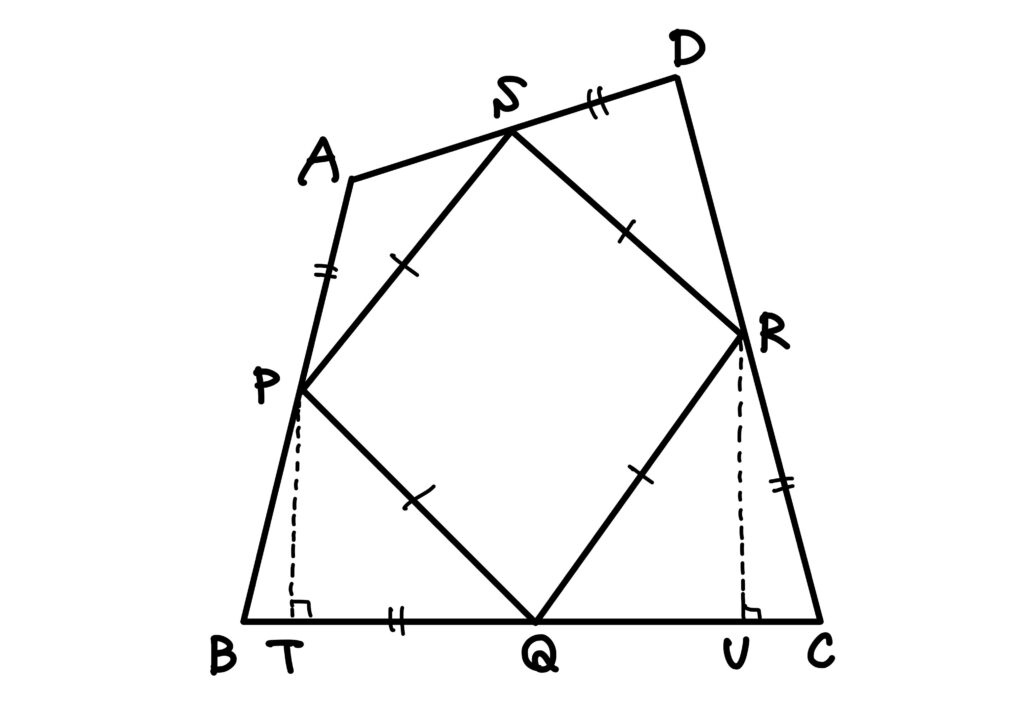
すると、
$$
\angle TQP+\angle UQR\equiv 90^\circ
$$
で、かつ
$$
\angle PTQ\equiv \angle QUR\equiv90^\circ
$$
だから、\(\angle TPQ\equiv \angle UQR\)かつ\(\angle TQP\equiv\angle URQ\)となります。
したがって、直角三角形の斜辺とその他の角が合同なので、\(\triangle TPQ\equiv\triangle UQR\)です。
故に、\(EQ\equiv FR\)です。
ここで、\(UR\leq CR\equiv BQ\)であるので\(TQ\leq BQ\)だから、
$$
\angle PBQ\leq \angle PTQ=90^\circ
$$
が成り立ちます。
すなわち、\(\angle B\leq 90^\circ\)ということです。
さて、これは\(\angle B\)に対してだけでなく、\(\angle A\)、\(\angle C\)、\(\angle D\)にも同様に適用できるので、
$$
\angle A,\ \angle B,\ \angle C,\ \angle D\leq 90^\circ
$$
が成り立ちます。
ここで、\(\angle A\)、\(\angle B\)、\(\angle C\)、\(\angle D\)は四角形\(ABCD\)の内角なので、
$$
\angle A+\angle B+\angle C+\angle D\equiv 360^\circ=90^\circ\times4
$$
が成り立ちます。
先程
$$
\angle A,\ \angle B,\ \angle C,\ \angle D\leq 90^\circ
$$
を導いたので、この2つから
$$
\angle A\equiv\angle B\equiv \angle C\equiv \angle D\equiv 90^\circ
$$
が成り立ちます。
ここまでくればもう簡単で、\(\triangle APS\)、\(\triangle BQP\)、\(\triangle CRQ\)、\(\equiv \triangle DSR\)は斜辺と他の一辺が合同ですので、
$$
\triangle APS\equiv \triangle BQP\equiv \triangle CRQ\equiv \triangle DSR
$$
となるため、四角形\(ABCD\)は正方形です。
投稿されたエレガントな解答
では、エレガントな解答を紹介します。
(前略)
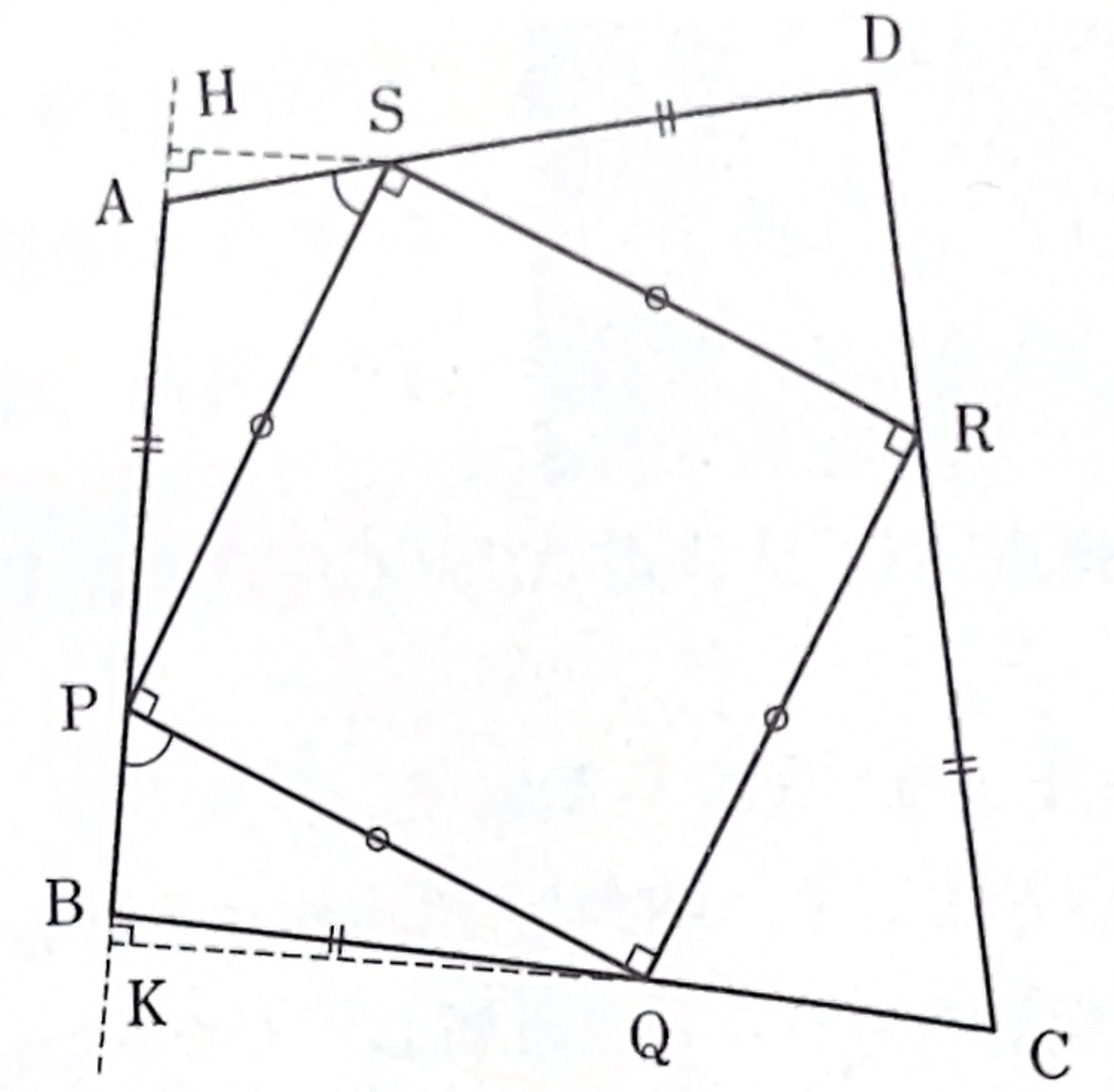
\(\angle A>90^\circ\)とか停止、\(S\)、\(Q\)から\(AB\)へ下ろした垂線の足を\(H\)、\(K\)とする。
\(\triangle HPS\)、\(\triangle KQP\)において
\begin{eqnarray}
\angle PHS&=&\angle QKP(=90^\circ),\quad PS=QP
\angle PSH&0&90^\circ-\angle HPS=\angle QPK
\end{eqnarray}
であるから、\(\triangle HPS\equiv\triangle KQP\)。
よって
$$
PH=QK\tag{1}
$$
\(\angle A>90^\circ\)と仮定したから、\(H\)は線分\(AP\)の\(A\)を超えた延長上にある。
よって
$$
PH>AP\tag{2}
$$
また\(QK\perp BP\)であるから
$$
QK\leq BQ.\tag{3}
$$
(1)、(2)、(3)をまとめて書けば
数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p87-88.
$$
AP<PH=QK\leq BQ
$$
よって\(AP<BQ\)。
これは\(AP=BQ\)に反する。故に\(\angle A>90^\circ\)ではない。すなわち
$$
\angle A\leq90^\circ.
$$
同じように\(\angle B>90^\circ\)、または\(\angle C>90^\circ\)、または\(\angle D>90^\circ\)として
$$
\angle B\leq90^\circ,\quad \angle C\leq90^\circ,\quad \angle D\leq90^\circ
$$
である。これらを辺々加えて
$$
\angle A+\angle B+\angle C+\angle D\leq 90^\circ\times4=360^\circ\tag{4}
$$
\(\angle A\leq90^\circ\)、\(\angle B\leq90^\circ\)、\(\angle C\leq90^\circ\)、\(\angle D\leq90^\circ\)のどの一つが等号を満たさなくてもそれらの和は\(360^\circ\)より小さくなる。すなわち(4)の等号が成り立つのは、\(\angle A\)、\(\angle B\)、\(\angle C\)、\(\angle D\)のすべてが\(90^\circ\)の場合に限る。ところで四角形の内角の和は\(360^\circ\)なので(4)の等号が成り立つから
$$
\angle A=\angle B=\angle C=\angle D=90^\circ
$$
である。
\(\triangle APS\)、\(\triangle BQP\)、\(\triangle CRQ\)、\(\triangle DSR\)は斜辺と1辺の等しい直角三角形であるから合同である。
よって
$$
AS=BP=CQ=DR
$$
これと\(AP=BQ=CR=DS\)から
$$
AB=BC=CD=DA
$$
よって四角形\(ABCD\)は正方形である。
本質的には筆者の解答とさほど変わらないな、と思いました。
筆者の解答は正攻法だったのでしょうか…
気持ち「筆者のほうが簡単では?」と思っちゃいました。
読者の皆様への挑戦状!
今から紹介する問題の解答は今週の土曜日に解説します!
\(\triangle ABC\)の\(\angle B\)、\(\angle C\)の2等分線が、それぞれ大変\(AC\)、\(AB\)と交わる点を\(D\)、\(E\)とするとき
$$
\angle ADE-\angle AED=60^\circ
$$
ならば、\(\angle ACB\)はどんな角でしょうか。数学セミナー編集部編(2001)『エレガントな解答をもとむ selections』日本評論社 p14.
結
いかがでしたか?
今回は数セミの「エレガントな解答をもとむ」に挑戦してみる、という記事でした。
読者の皆様も是非一度挑戦してみて下さい!
そして、「読者の皆様への挑戦状」にも是非挑戦していただき、解答をコメントで教えて下さい!
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければ全てお答えします!
お問い合わせの内容にもよりますが、ご質問はおおよそ3日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする