本記事の内容
本記事は、基本情報技術者試験におけるオートマトンについて、情報及びコンピュータの素人目線から説明する記事です。
本記事を読むに当たり、ビットについて知っている必要があるため、以下の記事も合わせてご覧ください。

イントロ
オートマトンの説明は一旦後回しにして、身近なオートマトンの例として自動販売機があります。
以下の文章はイメージとして自動販売機を思い浮かべて御覧ください。
自動販売機にはボタンがたくさんあるので、複雑なシステムのように見えます。
しかし、自動販売機の本質的な役割を図示してみると意外とシンプルだったりします。
モデル化
モデル化、モデル
モデル化とは、現実世界にある複雑なモノを単純化してわかりやすくすることを指す。また、単純化したモノをモデルと呼ぶ。数学でもモデルやらモデル化やらという言葉は出現しますが、本質的には上記のことを指します。
単純化の手法として数式を使う、だのの話になってくるということです。
オートマトン
オートマトン
オートマトンとは、機能を「入力」「状態」「出力」の3つで表すシステムのモデルを指す。自販機を思い浮かべてみましょう。
自販機のオートマトンの入力、状態、出力はそれぞれ以下です。
- 入力:自販機に入れるお金
- 状態:入れたお金の合計金額
- 出力:自販機から出てくる商品
余談(オートマトンの本来の意味)
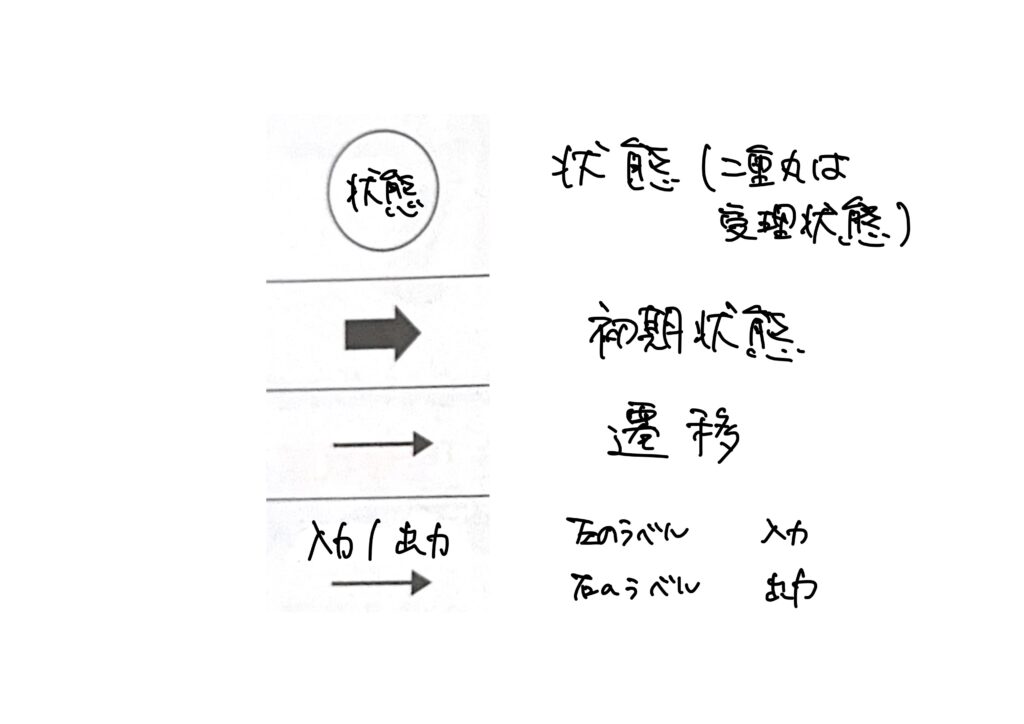
オートマトンとは、ギリシャ語で「自らの意思で動くもの」という意味です。状態遷移表
オートマトンにおける「状態」は、時間や動作に寄って初期状態からいくつかの状態を遷移して、最終的な状態に行き着きます。
この、最終的な状態を「受理状態」といいます。
また、このような状態の遷移を表で表したものを状態遷移表、図で表したものを状態遷移図といいます。
状態遷移表
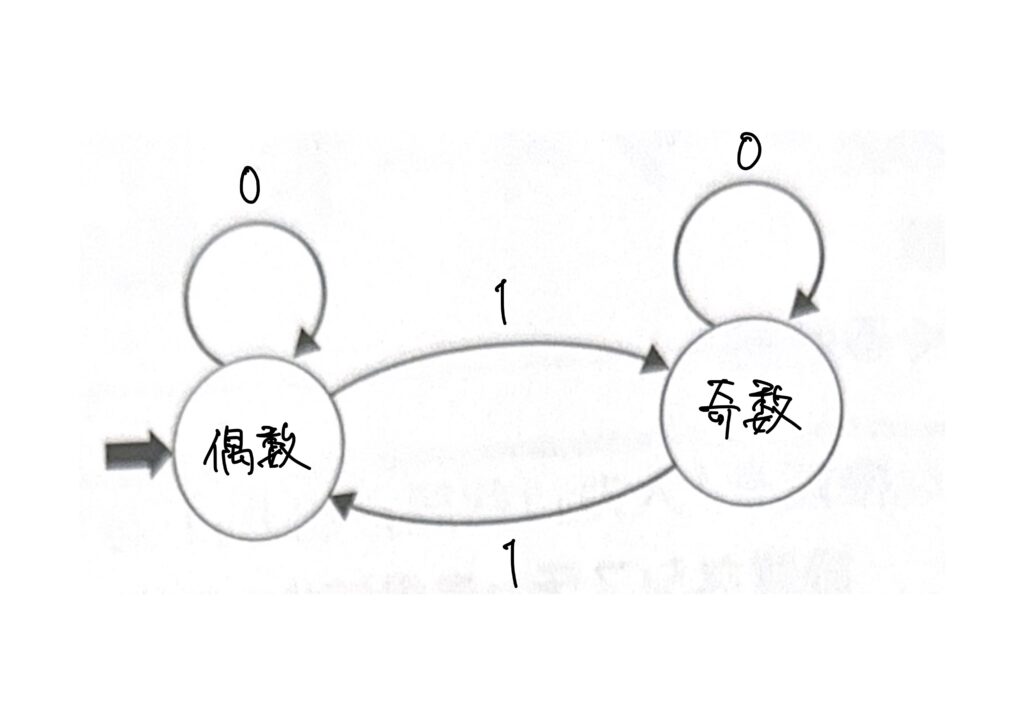
状態遷移表とは、状態の変化を表す図である。例えば、0か1を入力値として取り、合計が奇数であるか、偶数であるかを表すシステムを考えてみましょう。
このシステムは以下の状態遷移表で表現できます。
| 現在の状態 | 0を足す | 1を足す |
| 偶数 | 偶数 | 奇数 |
| 奇数 | 奇数 | 偶数 |
例えば、この場合、偶数に0を足せば偶数という状態になり、偶数に1を足せば奇数という状態になる事がわかります。
状態遷移図
状態遷移図
状態遷移図とは、状態の変化を示す図である。先程の状態遷移表を状態遷移図で表すと、次の図になります。
例題
では、オートマトンの例題を解いてみます。
次の状態遷移図で表現されるオートマトンで受理されるビット列はどれか。ここで、ビット列は左から順に読み込まれるものとする。
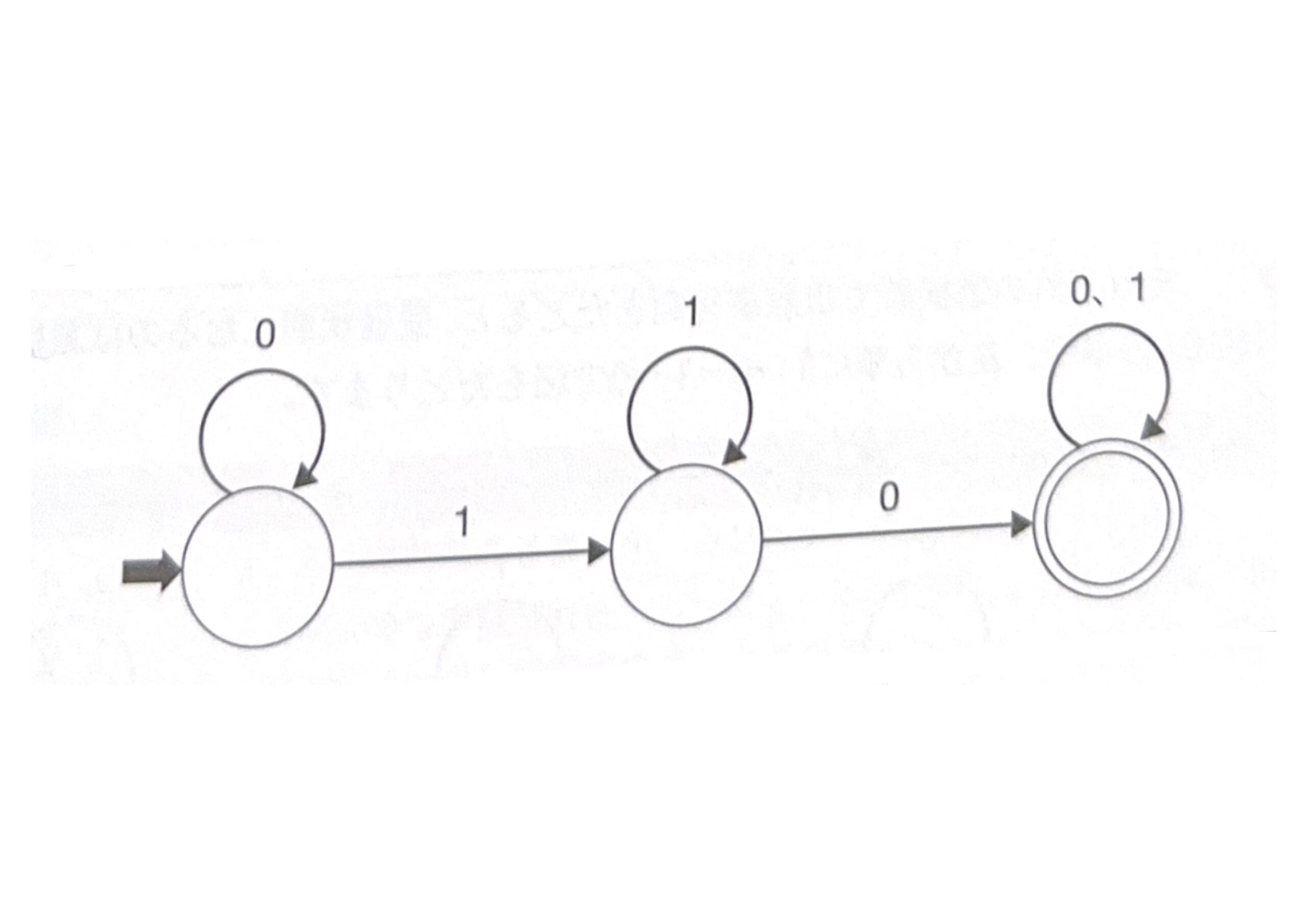
- 0000
- 0111
- 1010
- 1111
一つずつ確かめてみると、次です。
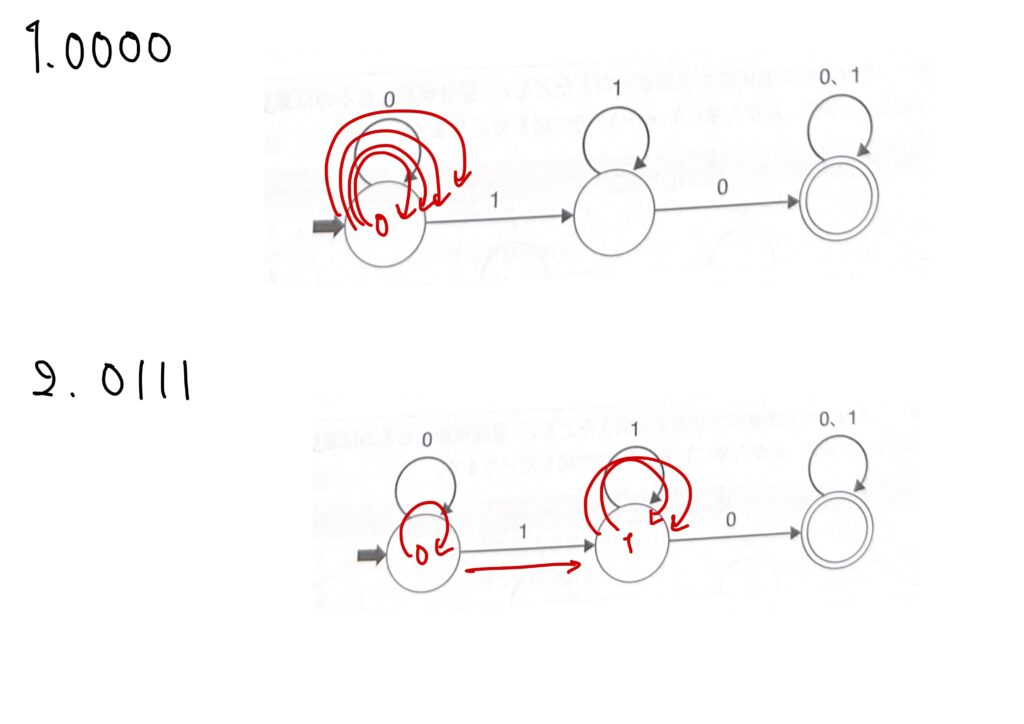

したがって、答えは3.です。
結
今回は、基本情報技術者試験におけるオートマトンについて、情報及びコンピュータの素人目線から説明しました。
オートマトンとは入力、状態、出力の3つで表すシステムのモデルでした。
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!



コメントをする