本記事の内容
本記事は、基本情報技術者試験における集合、論理演算、論理回路、オートマトンについて、情報及びコンピュータの素人目線から説明する記事です。
本記事を読むに当たり、特別必要な知識はありません。
前回の記事(データの単位、基数変換、負の2進数、2進数の四則演算)は以下をご覧ください!
本ブログでは集合・論理・写像や実数の連続性、群論やグラフ理論など基礎的な大学数学(主として大学1,2年向けの数学)を解説しておりますので、そちらの記事もぜひご覧ください!
集合と論理演算
これは別シリーズの記事(論理と集合シリーズ)を読んでいただければ網羅できます。
ただ、数学に大きく寄っているため、この章では超特急(もはや新幹線)で必要な部分だけ述べることにします。
本章で言いたいこととしては
ベン図は非常に強力なツールである
ということです。
集合とベン図
“本章において”、集合とベン図はそれぞれ何者か、というと次です。
集合、ベン図
- 集合 区別できる条件でグループわけされたモノの集まりを集合という。また、集合を構成するここのモノを要素という。
- ベン図 集合の関係を視覚的に表した図をベン図という。
数学的に厳密な話とは別で、直感的なものですが、「問題が解ける」という意味ではこれで十分です。
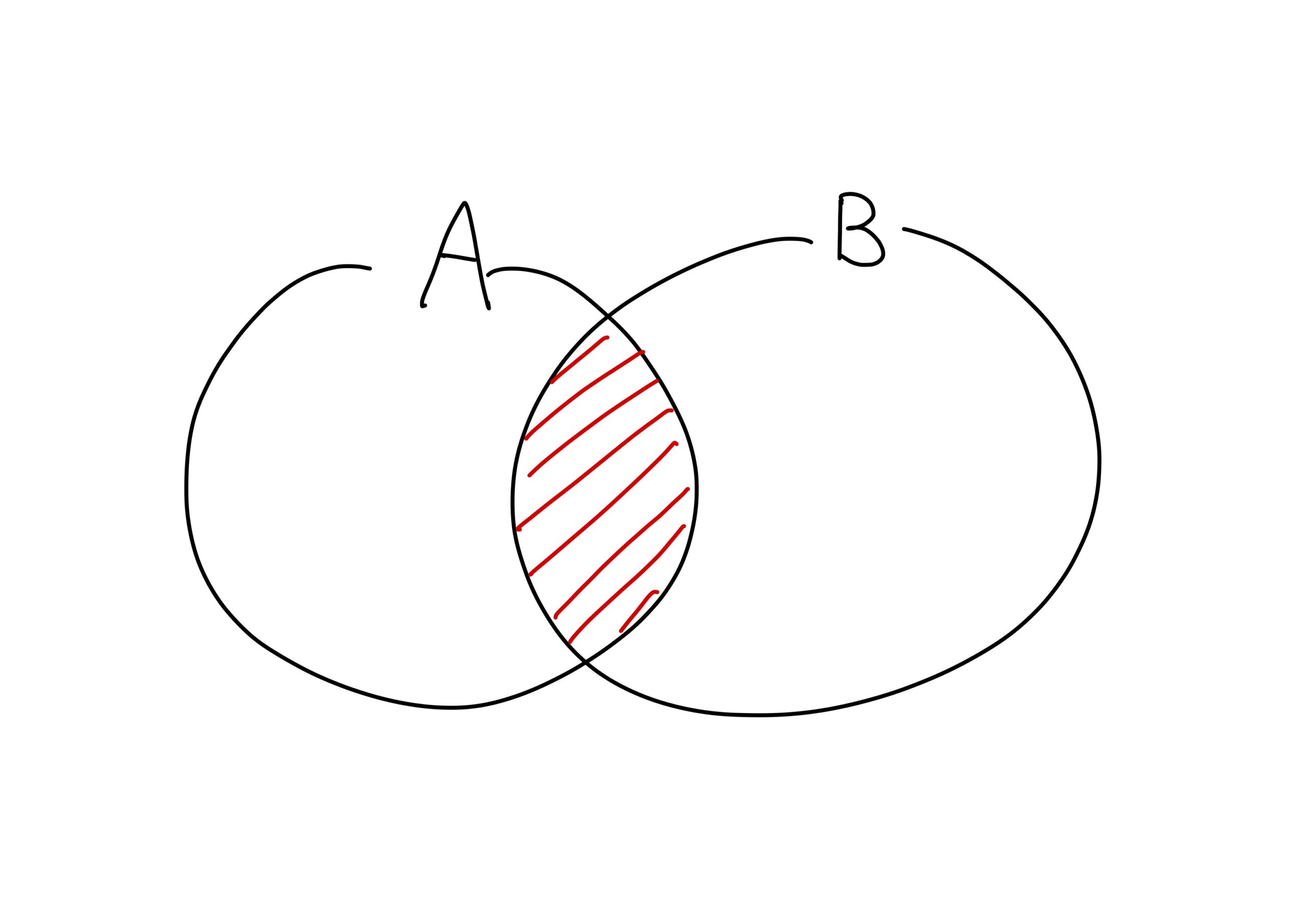
集合の関係はいくつもありますが、代表的かつ試験で出題されるのは以下の3種類です。
- 積集合:\(A\cap B\)
- 和集合:\(A\cup B\)
- 補集合:\(\bar{A}\)


論理演算
我々が日常で使う\(+,-,\times,\div\)は四則演算と呼ばれる演算です。
しかし、コンピュータの世界では2進数であるため、\(0\)と\(1\)(電圧が低い、高い)という2種類しか表現出来ません。
故に、コンピュータの世界では直接四則演算を行うことは出来ないのです。
そこで、コンピュータに計算させるために応用されたのが論理演算です。
コンピュータは論理演算を組み合わせることによって、四則演算を始め、様々な計算を行います。
論理演算の基本
論理演算
2進数の1桁のみを対象とした演算方式を論理演算という。つまり、論理演算が扱う数字は0と1の二種類だけであり、その結果も常に0か1かということです。
四則演算は\(+,-,\times,\div\)の4種類でした。
論理演算の主たる演算はAND、OR、XOR、NOTの4種類です。
四則演算の結果は無限に存在するため表にまとめることは出来ませんが、論理演算の計算結果は有限個しか存在しないため、次のようにまとめることが出来ます。
(※数学のご経験がある方であれば、「0を偽、1を真と捉えれば単純に論理の話ね」と感じると思います。)
| A | B | A AND B | A OR B | A XOR B | NOT A |
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
| 演算子 | 論理式 | 説明 |
| AND | A\(\cdot\)B | AとBの双方が「1」のときに、「1」を出力する論理演算。論理積とも呼ばれる。 |
| OR | A\(+\)B | AとBの少なくとも一方が「1」のときに、「1」を出力する論理演算。論理和とも呼ばれる。 |
| XOR | A\(\oplus\)B | AとBの値が異なる場合に「1」を出力し、値が同じ場合には「0」を出力する論理演算。排他的論理和とも呼ばれる。 |
| NOT | \(\bar{A}\) | 0が入力なら1を出力し、1が入力なら0を出力する論理演算。否定とも呼ばれる。 |
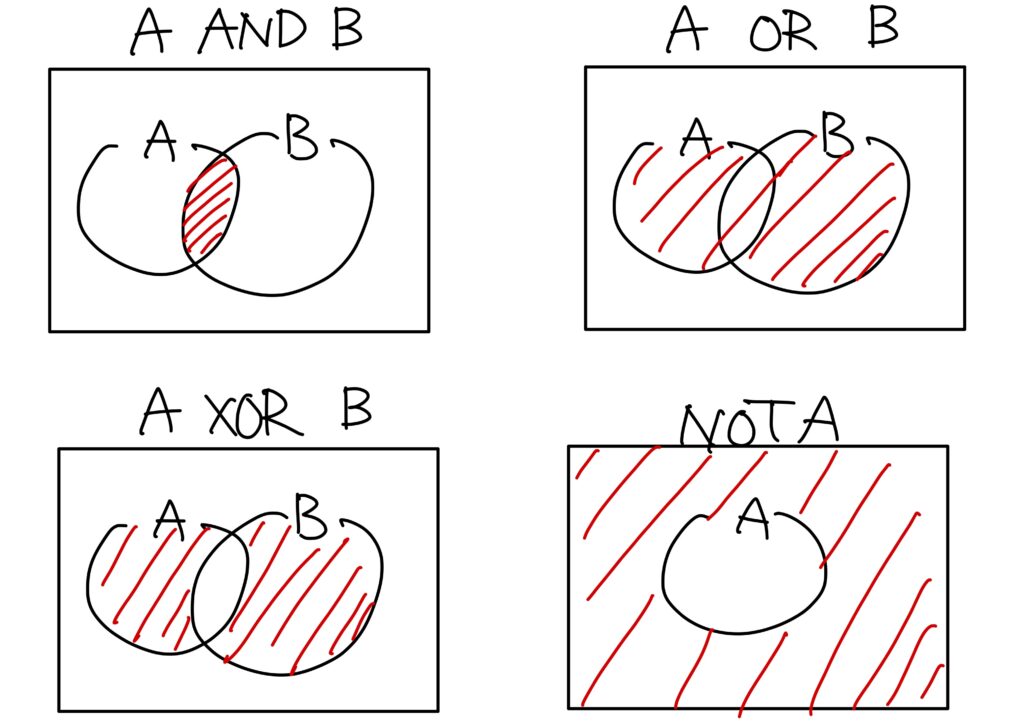
「え?これ、覚えるの?」というと覚えます。
ただ、この表をまるっと覚えるのは骨が折れますので、ベン図で視覚的に覚えるのが良いと思います。
NANDとNOR
上記の4つの演算子が論理演算の基本演算ですが、基本情報技術者試験では、上記の他にNAND(なんど、否定論理積)とNOR(のあ、否定論理和)があります。
ただ、非常に単純です。
NANDは、ANDを否定しただけですし、NORはORを否定しただけです。
つまり、
- A NAND B = NOT (A AND B)
- A NOR B = NOT (A OR B)
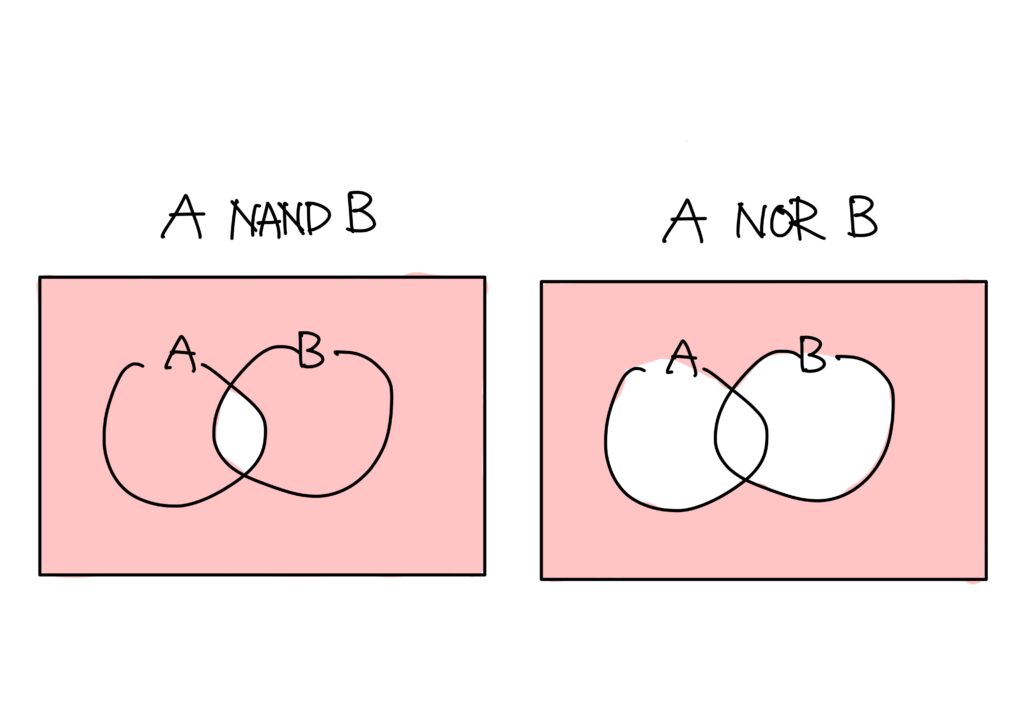
という単にそれだけです。
したがって、真理値表とベン図は以下のようになります。
| A | B | A AND B | A OR B | A NAND B | A NOR B |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 |
論理演算子の優先順位
四則演算では
カッコ → \(\times\)と\(\div\) → \(+\)と\(-\)
という優先順位がありました。
論理演算にも優先順位があります。
結論としては以下です。
(基本情報技術者試験における)論理演算の優先順位
実は、論理演算の優先順位には細かいルールがありますが、基本情報技術者試験で覚えておく必要がある順位としては上記だけです。
ちょっとだけ観察してみると、ANDは論理積とも呼びますし、ORは論理和とも呼ぶので、四則演算の順位と似ていますね。
例1. 「A OR B AND C」という論理演算の処理の順番
この場合、まず「B AND C」がまず処理され、その後にORの処理が実行されます。
ベン図で描けば次です。
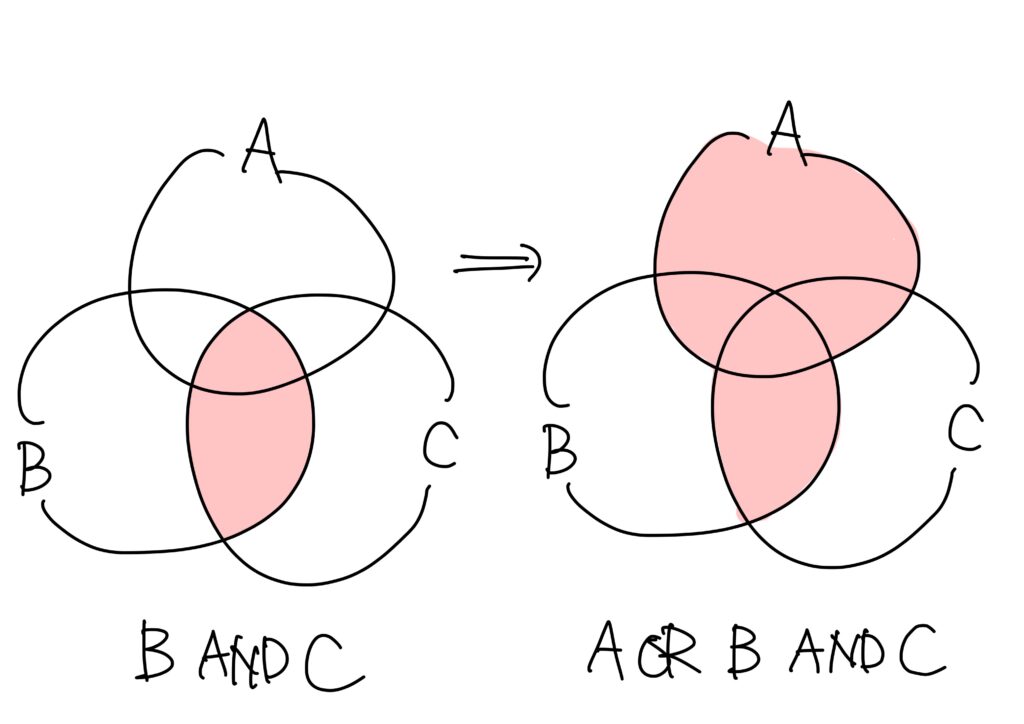
もし、仮に順番を変えてみると、
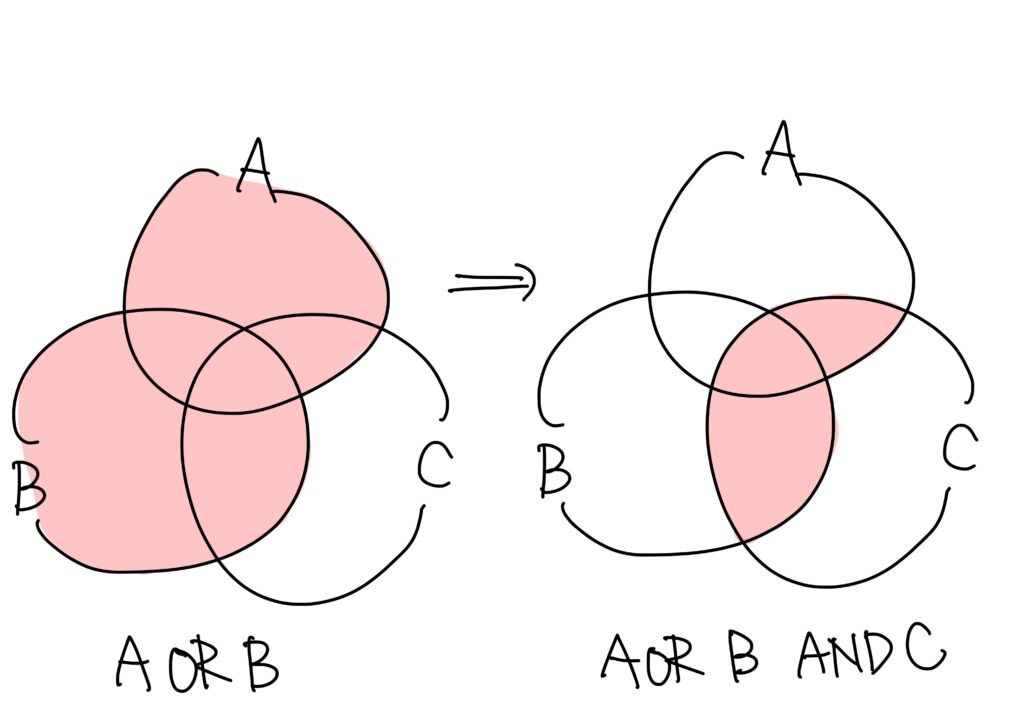
となってしまって、全く別の答えになってしまいますので、注意です。
例題
XとYの否定論理積X NAND Yは、NOT(X AND Y)で定められる。X OR YをNANDだけを使って表した論理式はどれか。
- ((X NAND Y) NAND X) NAND Y
- (X NAND X) NAND (Y NAND Y)
- (X NAND Y) NAND (X NAND Y)
- X NAND (Y NAND (X NAND Y))
論理演算の問題が出たらば、ベン図で解きます。
目標はXとYの和集合です。
これを意識して各選択肢をベン図で表現すれば以下です。
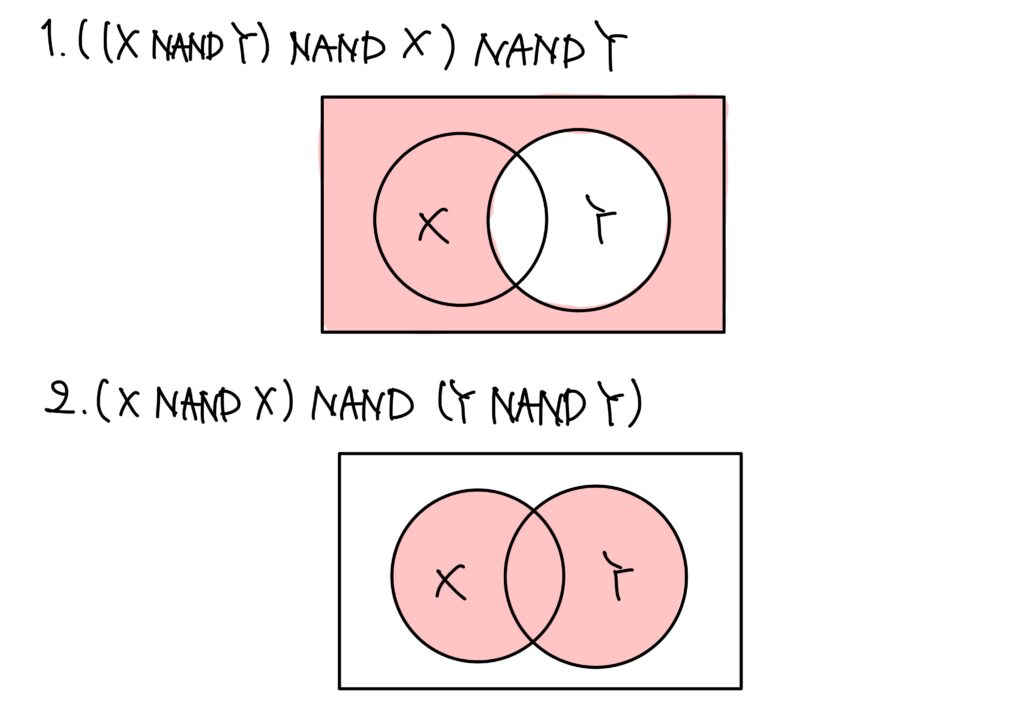
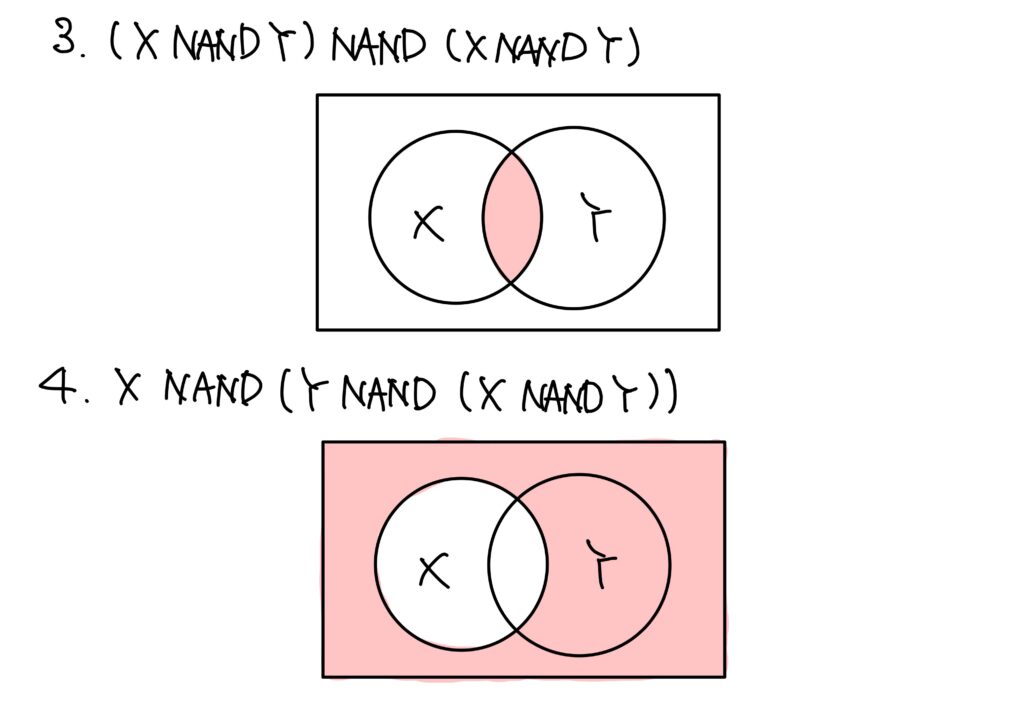
したがって、答えは2.です。
論理回路
CPU(※)の内部は無数の電子回路によって構成されています。
この電子回路はとても小さくて、電子回路の幅を髪の毛くらいに拡大すれば、CPUの大きさは東京ディスニーランドと同じくらいの大きさになります。
ちなみに、CPUの大きさは指でつまめるくらいです。(ご興味があれば調べてみてください)
※CPU
詳しくはのちの記事で述べますが、CPUを人間の臓器に例えれば「脳」です。コンピュータにあらゆる命令を下す部品がCPUです。
「CPUが脳みそだったとすると、PCの図体からして脳がちっちゃいのに随分と頭いいな、コンピュータって」と思いました。
論理回路
論理回路
論理回路とは、論理演算を行う電子部品である。論理演算とは、AND、OR、XOR、NOTでしたね。
コンピュータの脳みそたるCPU(中央処理装置※後の記事で述べます)は非常に多くの論理回路を使って演算をしています。
MIL記号
実物の論理回路は電子部品なわけですが、論理回路を紙面上に表す際の記号をMIL記号(みるきごう)といいます。
以下に、主たるMIL記号を列挙しますが、記号を覚える必要はありません。
なぜかというと、問題用紙に必ず記法の意味が掲載されるからです。(覚えちゃったほうが早いですが、覚えなくてOKです)
ただ、記号の意味は覚える必要があります。
「ANDってなんだったけなあ」というのは覚える必要がある、という意味です。
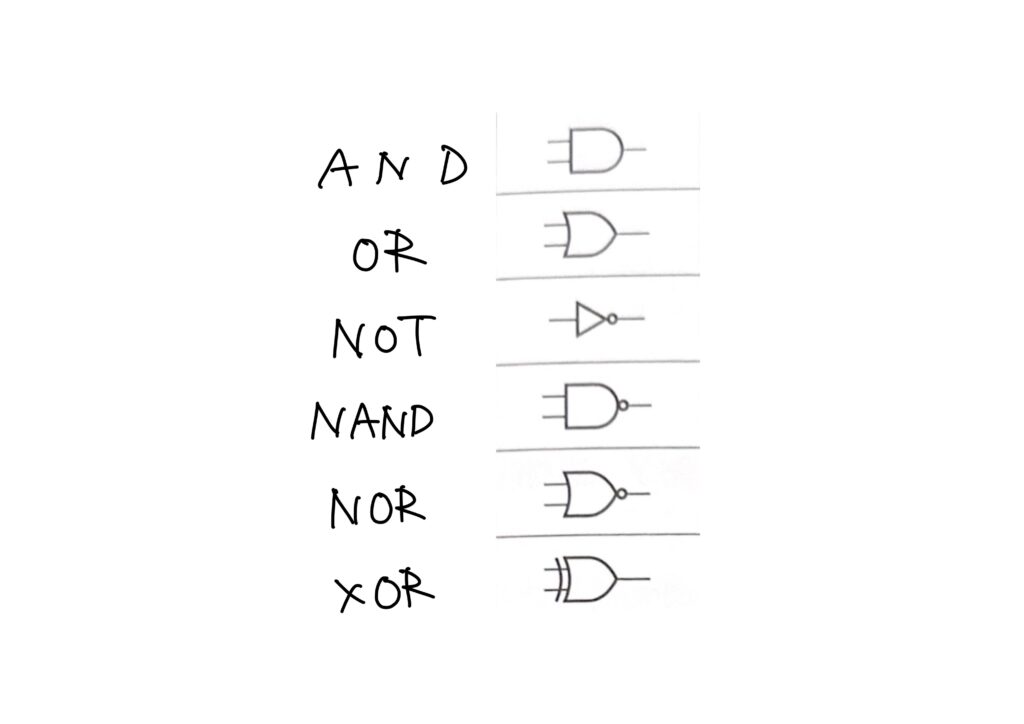
MIL記号による論理積の演算を例としてみてみましょう。
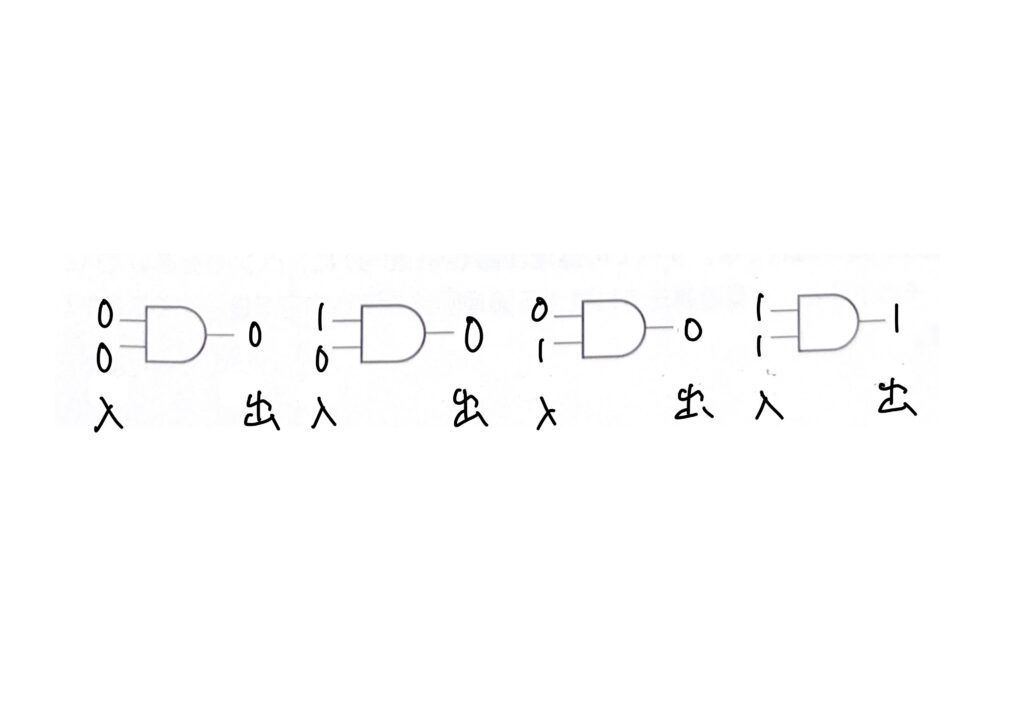
論理回路の問題の解き方
図の論理回路と等価な回路はどれか。
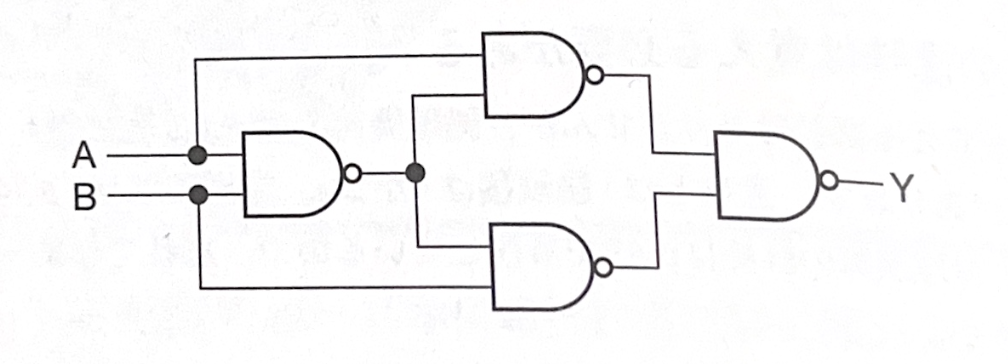
回答の形式としては、設問の論理回路と同じ意味を持つMIL記号、論理式、真理値表のいずれかを選択する問題として出題されます。
論理回路の問題はベン図で
論理回路の問題は複雑に見えますが、ベン図で処理することで視覚的にもわかりやすく解くことが出来ます。

以上のことから、排他的論理和(XOR)と同じベン図になっている事がわかるので、答えは3.です。
一つずつ、地道にやると簡単に解けます。
加算回路
今まで学習した論理回路を組み合わせることで、ようやくCPUは足し算ができるようになります。
つまり、この節ではCPUがどのようにして足し算をしているかがわかります。
加算回路
2進数の足し算を行う論理回路を加算回路という。加算回路には、
- 半加算器
- 全加算器
の2種類が存在します。
半加算器
半加算器
半加算器は、2進数の足し算において、下の位からの桁上りを考慮しない加算回路を指す。文章だとわかりにくいので、具体的な値で考えてみます。
2進数は0と1の2種類の数しか使わないので、2つの2進数の足し算は本質的には
- \(0+0=1\)
- \(0+1=1\)
- \(1+0=1\)
- \(1+1=10\)
の4種類だけです。

これら4つの演算を、4つの文字(X、Y、C、S)を使ってX+Y=CSと表現したとします。
これを真理値表に表すと次です。
| 入力 | 入力 | 出力 | 出力 |
| X | Y | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
この半加算器の真理表は、論理積(AND)と排他的論理和(XOR)を組み合わせで作ることが出来ます。
以下が半加算器の論理回路です。
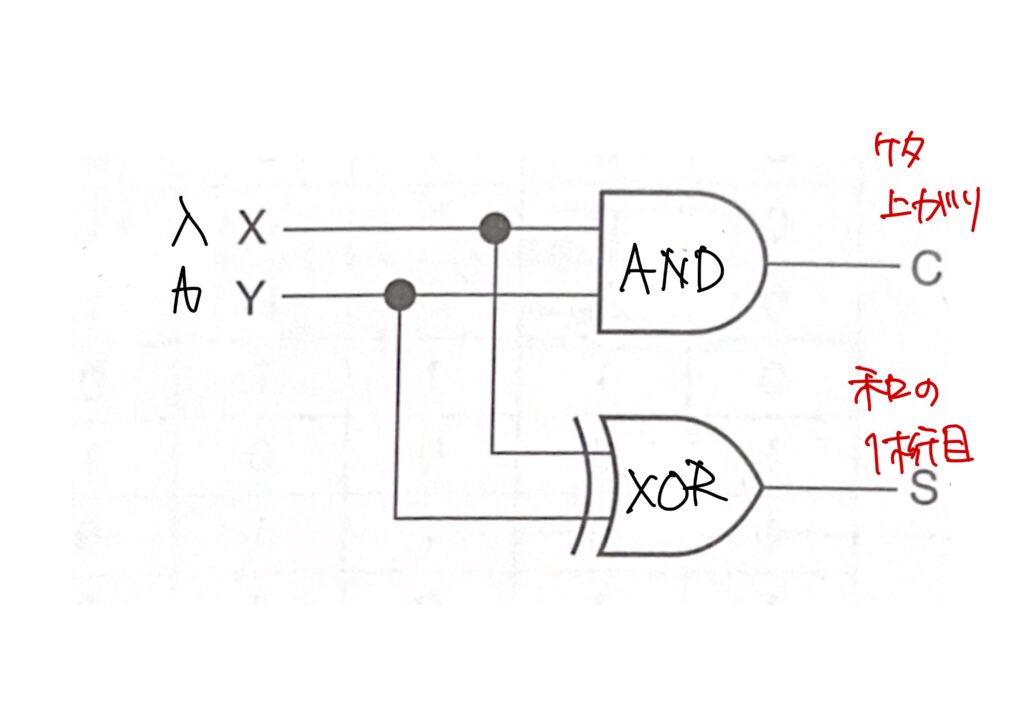
全加算器
全加算器は、半加算器が下の位からの桁上りを考慮しない加算回路であったのに対し、桁上りを考慮する加算回路です。
全加算器
下の位からの桁上りを考慮する加算回路を全加算器という。半加算器の入力は2つでしたが、全加算器は桁上りの分の情報が増えるため、3つの入力が必要になります。
3つの2進数の足し算は以下の8パターンです。
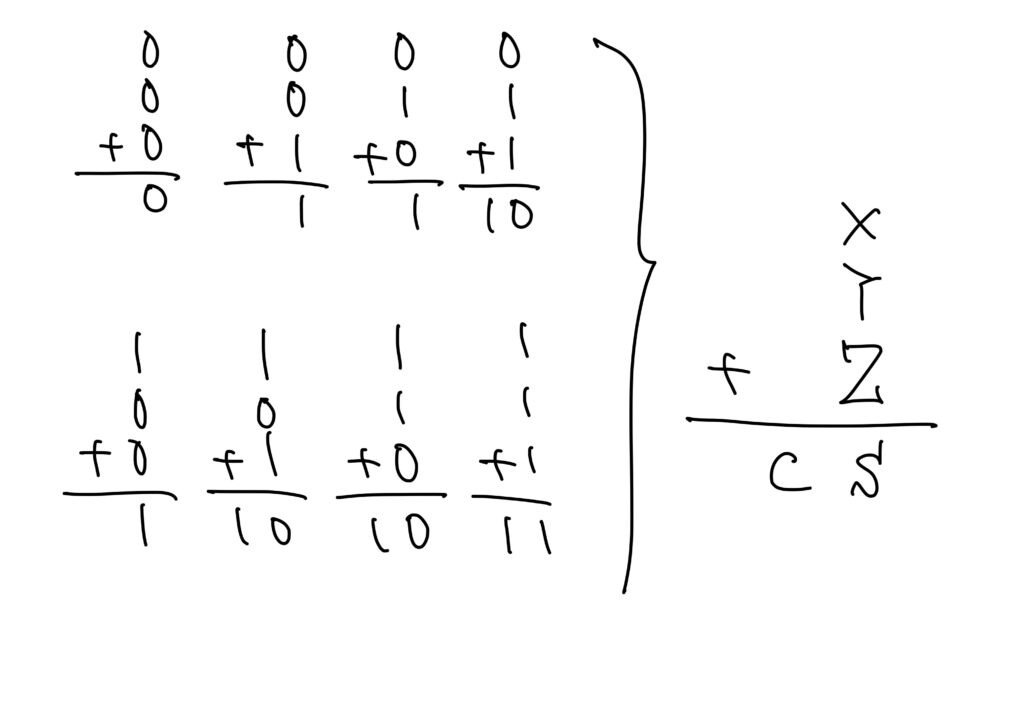
この8つの計算を、半加算器のときと同様にして5つの記号(X、Y、Z、C、S)を使って真理値表に表すと次です。
| 入力 | 入力 | 入力 | 出力 | 出力 |
| X | Y | Z | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
全加算器の真理値表は、2つの半加算器と、1つの論理和(OR)の組み合わせで作ることが出来ます。
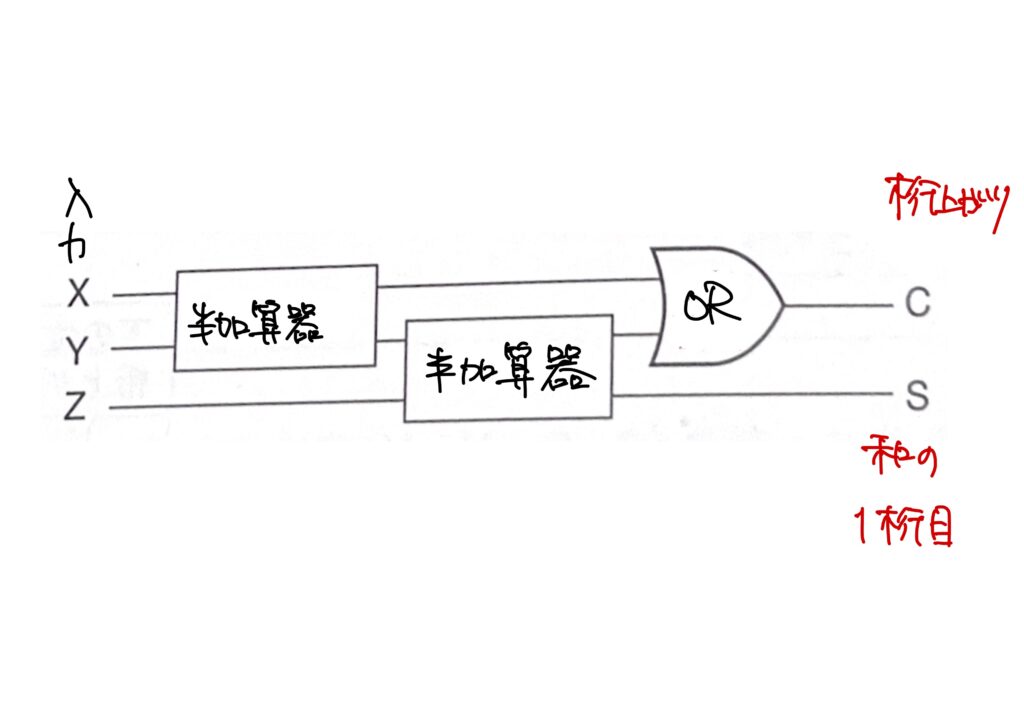
計算式の表し方
「そんなの\(1+2=3\)という表記だけじゃない?」と思われるかもしれませんが、コンピュータの世界では別の表現方法があります。
といっても、本質的には演算子の場所がどこか?という話です。
実は、計算式を表す方法には
- 中置記法
- 前置記法(ポーランド記法)
- 後置記法(逆ポーランド記法)
の3つが存在します。
中置記法
中置記法
中置記法とは、数字の間に演算子を置く計算式の記法である。とどのつまり、我々が普段使っている記法のことです。
$$
1+2=3
$$
がまさにそうです。
前置記法
前置記法
前置記法とは、数字の前に演算子を置く計算式の記法である。中置記法での\(1+2\)を前置記法で書くと、
$$
+1 2
$$
となります。
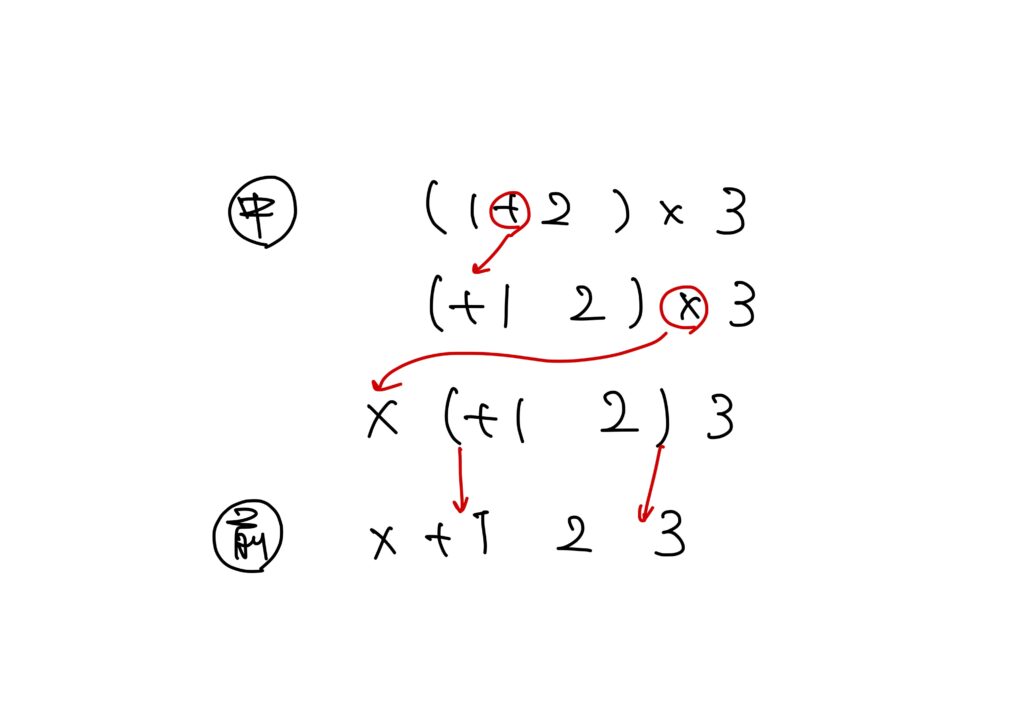
前置記法では、数と数をスペースで区切ります。
スペースがなければ、先の例で言えば12(じゅうに)と読めてしまうからです。
前置記法を用いれば、数式にカッコを付ける必要がなくなるというのが前置記法のメリットです。
例えば、中置記法の\((1+2)\times3\)を前置記法にすると、以下のようになります。
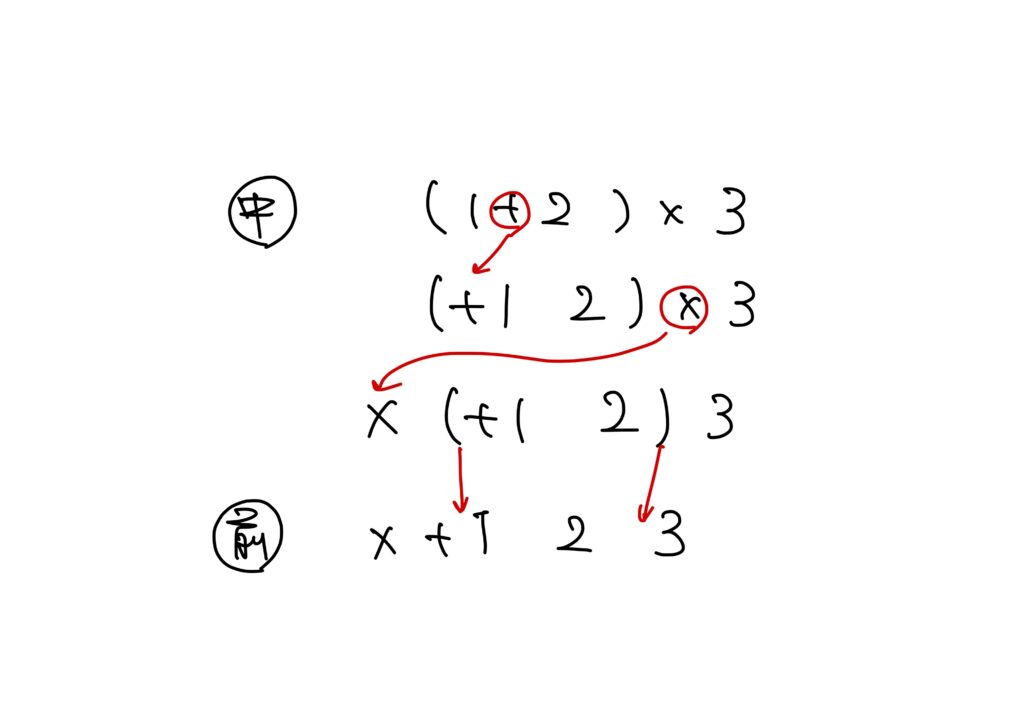
中置記法を前置記法に変換するには、計算の優先順位が高い演算子から順々に前に出し、最後にカッコを取ります。
優先順位は、四則演算と同様で
カッコ → 掛け算、割り算 → 足し算、引き算
です。
後置記法
前置記法
前置記法とは、数字の後ろに演算子を置く計算式の記法である。表記のルールとしては、演算子を後ろに置くこと以外前置記法と同じです。
後置記法は逆ポーランド表記法とも呼ばれます。
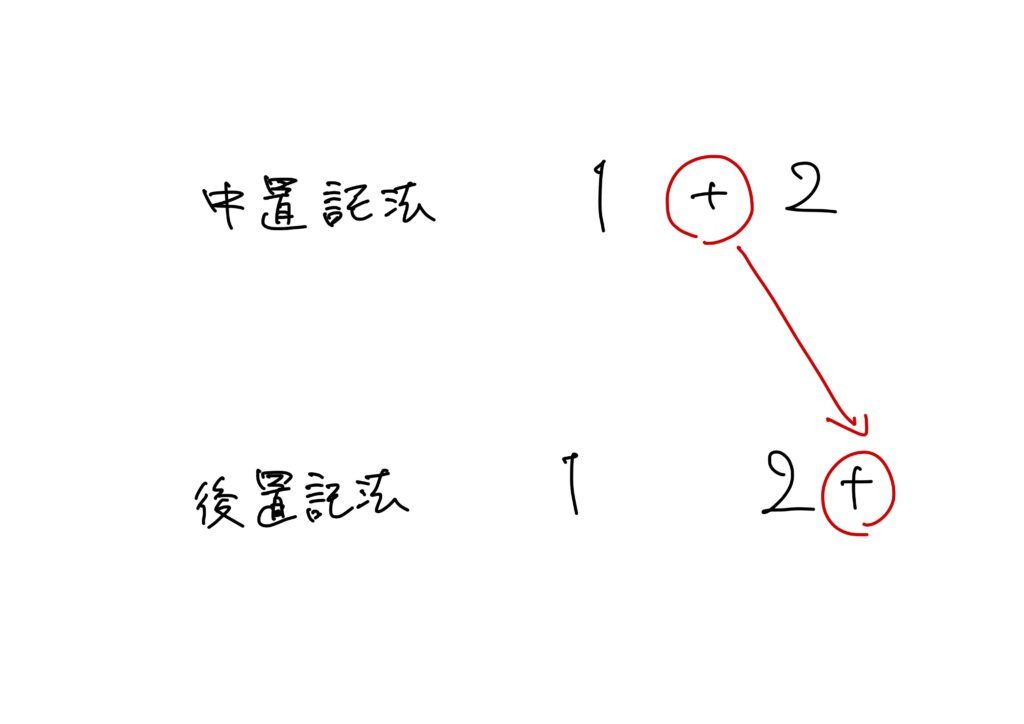
なんでこんな記法が必要なのか?
「何故か?」という問の答えは、コンピュータ内部で使われている表記方法だから、です。コンピュータは逆ポーランド表記法とスタックの仕組み(後の記事で)を組み合わせて計算を行っています。
オートマトン
オートマトンの説明は一旦後回しにして、身近なオートマトンの例として自動販売機があります。
以下の文章はイメージとして自動販売機を思い浮かべて御覧ください。
自動販売機にはボタンがたくさんあるので、複雑なシステムのように見えます。
しかし、自動販売機の本質的な役割を図示してみると意外とシンプルだったりします。
モデル化
モデル化、モデル
モデル化とは、現実世界にある複雑なモノを単純化してわかりやすくすることを指す。また、単純化したモノをモデルと呼ぶ。数学でもモデルやらモデル化やらという言葉は出現しますが、本質的には上記のことを指します。
単純化の手法として数式を使う、だのの話になってくるということです。
オートマトン
オートマトン
オートマトンとは、機能を「入力」「状態」「出力」の3つで表すシステムのモデルを指す。自販機を思い浮かべてみましょう。
自販機のオートマトンの入力、状態、出力はそれぞれ以下です。
- 入力:自販機に入れるお金
- 状態:入れたお金の合計金額
- 出力:自販機から出てくる商品
余談(オートマトンの本来の意味)
オートマトンとは、ギリシャ語で「自らの意思で動くもの」という意味です。状態遷移表
オートマトンにおける「状態」は、時間や動作に寄って初期状態からいくつかの状態を遷移して、最終的な状態に行き着きます。
この、最終的な状態を「受理状態」といいます。
また、このような状態の遷移を表で表したものを状態遷移表、図で表したものを状態遷移図といいます。
状態遷移表
状態遷移表とは、状態の変化を表す図である。例えば、0か1を入力値として取り、合計が奇数であるか、偶数であるかを表すシステムを考えてみましょう。
このシステムは以下の状態遷移表で表現できます。
| 現在の状態 | 0を足す | 1を足す |
| 偶数 | 偶数 | 奇数 |
| 奇数 | 奇数 | 偶数 |
例えば、この場合、偶数に0を足せば偶数という状態になり、偶数に1を足せば奇数という状態になる事がわかります。
状態遷移図
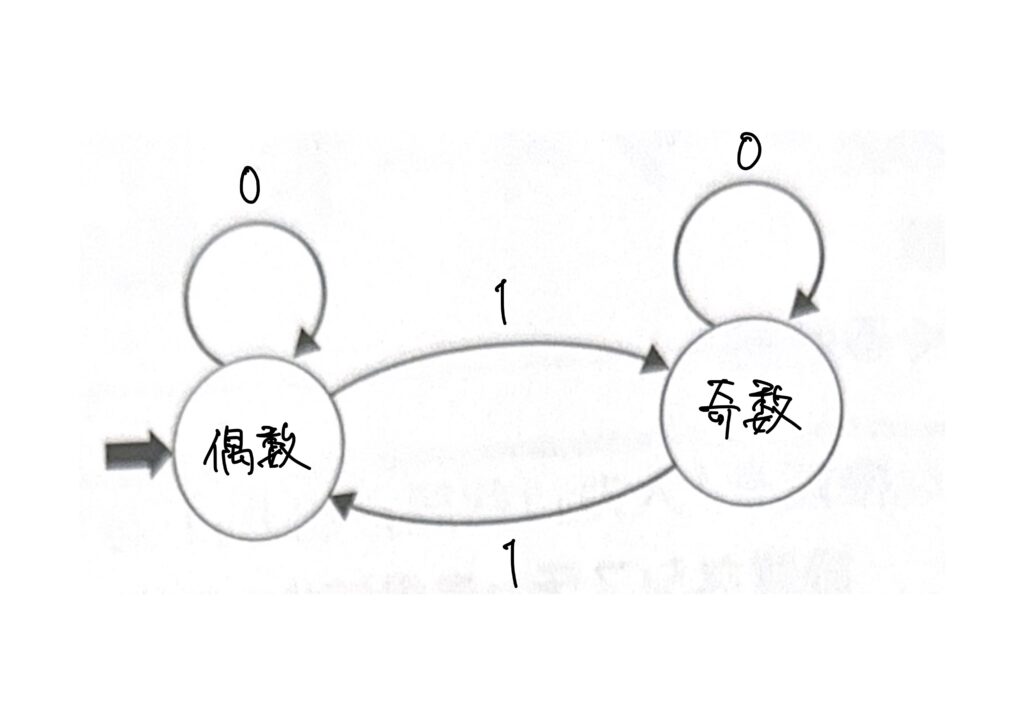
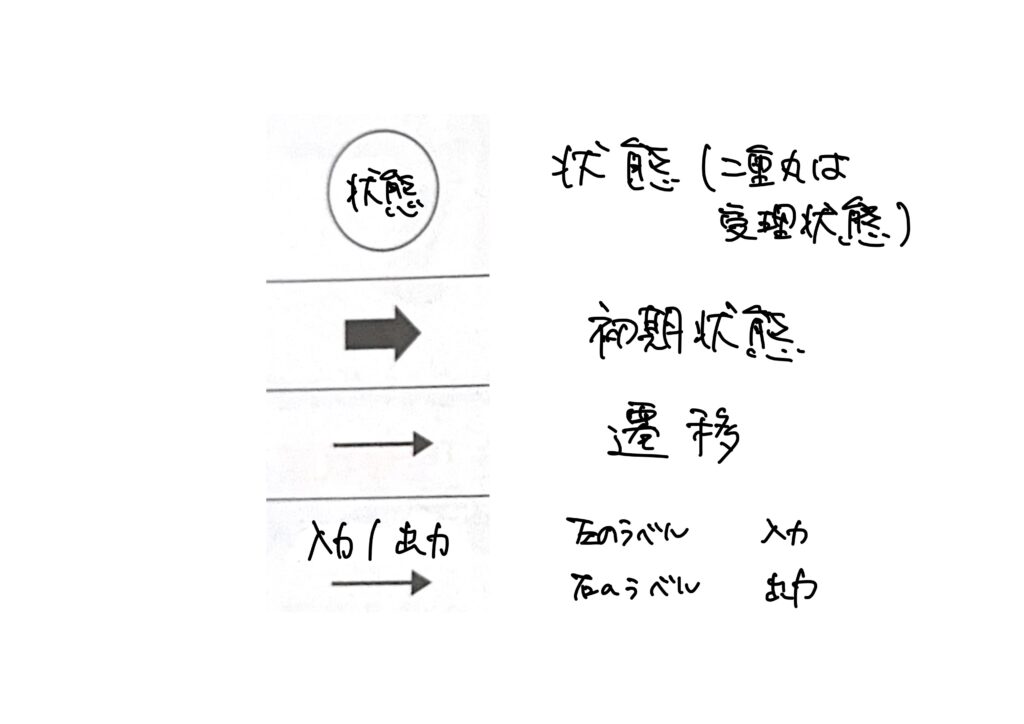
状態遷移図
状態遷移図とは、状態の変化を示す図である。先程の状態遷移表を状態遷移図で表すと、次の図になります。
例題
では、オートマトンの例題を解いてみます。
次の状態遷移図で表現されるオートマトンで受理されるビット列はどれか。ここで、ビット列は左から順に読み込まれるものとする。
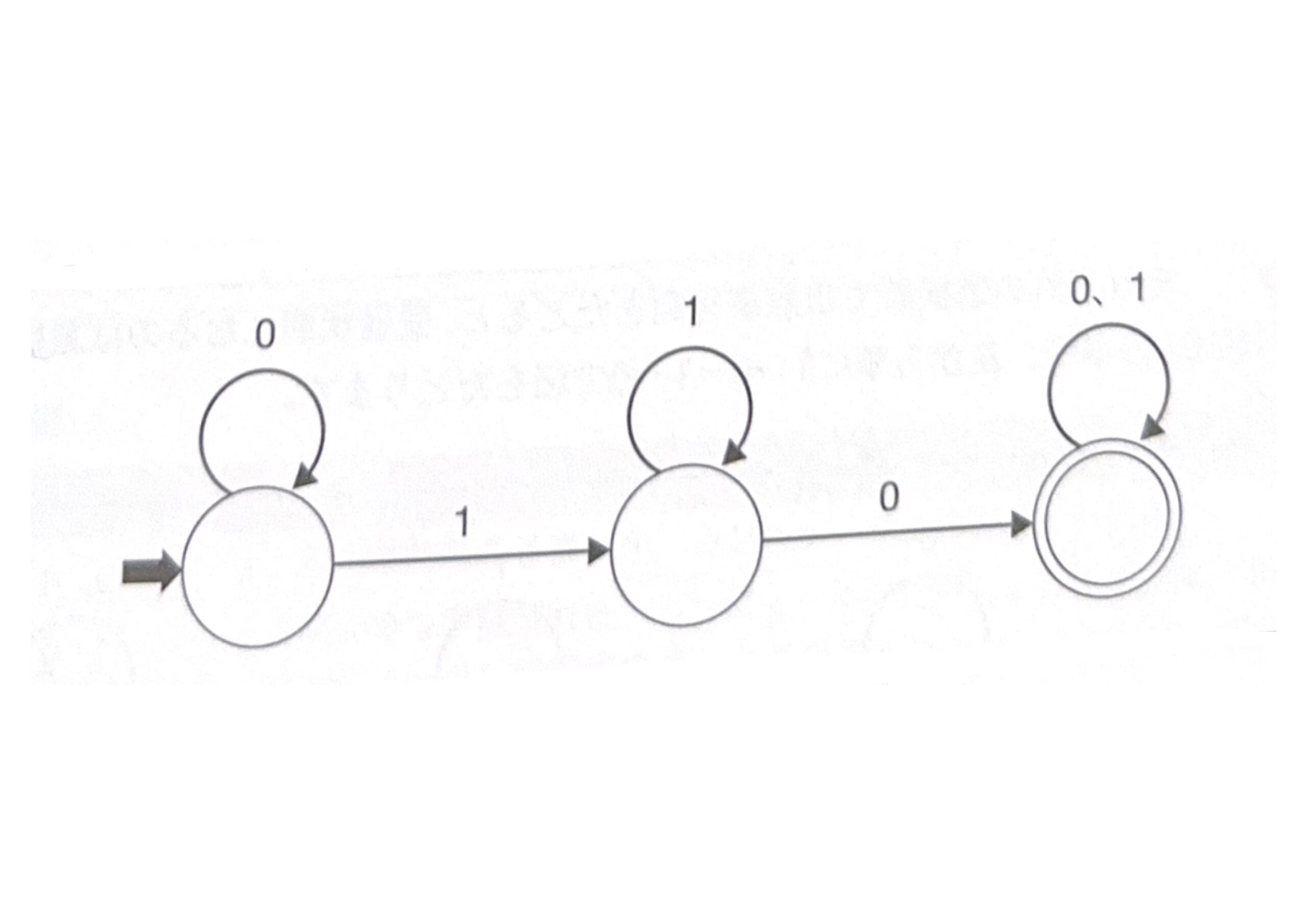
- 0000
- 0111
- 1010
- 1111
一つずつ確かめてみると、次です。
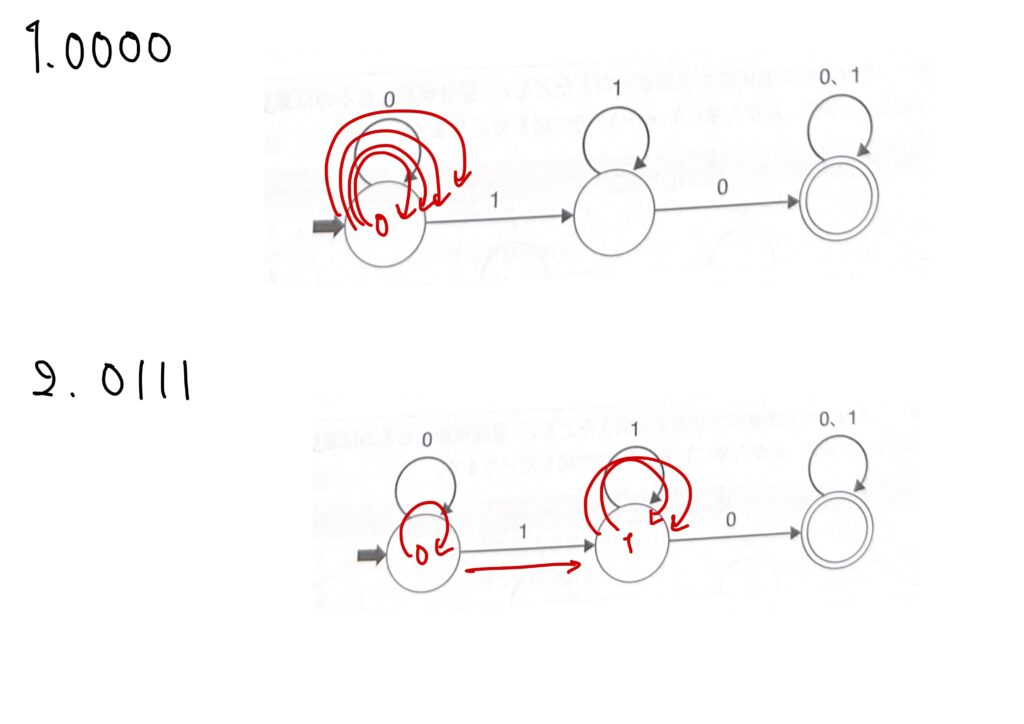

したがって、答えは3.です。
結
今回は、基本情報技術者試験における集合、論理演算、論理回路、オートマトンについて、情報及びコンピュータの素人目線から説明しました。
問題が解けるということに重きを置き説明しました。
論理演算にはAND、OR、XOR、NOTの4種類、論理回路には半加算器と全加算器があるのでした。
オートマトンとは入力、状態、出力の3つで表すシステムのモデルでした。
質問、コメントなどお待ちしております!
どんな些細なことでも構いませんし、この記事に限らず、「定理〇〇の△△が分からない!」などいただければお答えします!
Twitterでもリプ、DM問わず質問、コメントを大募集しております!





コメントをする