本記事の内容
本記事は「行列とは何か?」「単位行列、正方行列とは何か?」「転置とは何か?」ということと、線型代数を学ぶ意味の一端を解説する記事です。
本記事を読むにあたり、基本的な予備知識として論理の初歩を知っている必要があるため、以下の記事も合わせて御覧ください。
※【論理と集合シリーズ】と銘打ってシリーズ化しているため、一部の記事のリンクを載せています。
線型代数学ってどんな分野?
「線型代数学はどんな分野かネ?」と言われると、安っぽいですが「一言で言うには難しい」です。
しかし、あえて言えば、数学、特に大学数学を学ぶ上で基礎的な分野だということはできます。
余談1.(読み飛ばしてOK)
表記の話ですが、「線型」という書き方と「線形」という書き方があります。これらは同じ意味です。
比較的新しい書籍は「線形」という書き方をして、比較的古い書籍は「線型」という書き方をしている印象があります。
これは流派みたいなもので、特に違いはありませんが、筆者は「線型」を好んで使っています。
というのも、「線の形(かたち)」よりも「線の型(かた)」のほうがしっくり来ているからです。
ちなみに、同様に「関数」も「函数」と書いたりもします。
「線形」だろうが「線型」だろうが、「関数」だろうが「函数」だろうが意味は同じなのでどっちでもいいんですけどね(笑)
「細かいところに勝手にこだわってんな(笑)」と思ってください。
個人的に線型代数を学ぶ目的は大きく分けて2つあると思っています。
それは
- 行列の対角化、三角化の理解
- 線型空間(ベクトル空間とも言います)、線型変換の理解
勿論、これだけでは有りません。(※余談2.参照)
さて、「線型代数学はどんな分野かネ?」という問の答えをはぐらかしていましたが、強いて言えば
です。
余談2.
筆者がこの記事を書こうと思ったときに、友人(まつもと)に「線型代数を学ぶ意味ってどうやって説明する?」と相談したところ、「難しいよね。線型代数って表情豊かなんだよね。」という主旨の助言をもらいました。なるほどな、と思いました。
線型代数というのは誠に基本的な分野である一方、その使い方はどの分野に使うかによって大きく変わります。
例えば、筆者の専門は幾何なのですが、幾何で使う線型代数と解析(特に数値計算など)で使う線型代数は異なります。
実際、解析学で使う線型代数は、筆者はあまり知りません(殆ど知らないと言ってもいいくらい)。
とはいえ、先に述べた「行列の性質と線型空間の性質を学ぶ分野ですよ〜」ということは変わりません。 なぜならば、数学の論を展開する上で、考える空間が線形空間だったりするからです(実際、多様体やらも線型空間から出発します)。
「じゃあ、結局行列の性質と線型空間の性質を一通りやったらOKってこと?」となるかもしれません。
おおよそ正解ですが、先の通り、線型代数は表情豊かですので、「これさえおさえておけばOK」ということではなく、必要になったらその時点で、必要なことをインプットしていく、ということを続ける必要がある分野だとも思います。
線型代数で扱う典型例
線型代数学で扱う典型的な例として、連立一次方程式の開放があります。
連立一次方程式は中学校で習うので「んなもん、加減法と代入法を使えばいいじゃん」と思うかもしれません。
確かに理論上そうですが、変数が\(10\)個あったらどうでしょうか(大げさかな?)。
勿論、加減法と代入法を繰り返し使うことで解を求めることができます(解が一意的に存在すれば)。
しかし、途轍もない計算が必要になります。
例えば、変数が\(3\)つだったらどうでしょうか。
$$
\begin{cases}
5x-4y+6z=8\\
7x-6y+10x=14\\
4x+9y+7z=74
\end{cases}
$$
これは勿論、加減法と代入法を駆使することで解が求まりますが、解こうとすると計算量がえらいことになります。
そして、「そもそもこの連立一次方程式は一意的な解が存在するのか?」ということも本来は確かめなければなりません。
それも含め、計算量がやべぇ事になります。
これを「行列」と呼ばれるものを導入して、その性質を使うことでよりスッキリ解くことができます。
そして、行列の性質を使って連立一次方程式を解くために必要なのが、対角化、三角化です(詳しくは、対角化、三角化の記事で解説します)。
ちょっとだけネタバラシをしましょう。
そもそも「行列って何?」という説明をしていないので、あまり意味は無いかもしれませんが….
先程の連立一次方程式を「行列」をつかって書くと次になります。
\begin{eqnarray}
\begin{cases}
5x-4y+6z=8\\
7x-6y+10x=14\\
4x+9y+7z=74
\end{cases}\quad\xrightarrow{行列を使って表現すると…}
\begin{pmatrix}
5&-4&6 \\
7&-6&10\\
4&9&7\\
\end{pmatrix}\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)
=\left(\begin{array}{c}
8\\
14\\
74
\end{array}\right)
\end{eqnarray}
これにおいて、
$$
\begin{pmatrix}
5&-4&6 \\
7&-6&10\\
4&9&7\\
\end{pmatrix}
$$
を係数行列と言ったりもしますが、これを行列の性質を使ってうまーく変形することで解を求めます。
また、「連立一次方程式の解が一意的に存在するか?」ということもこの係数行列を観察することで導くことができます。
具体的にどうするか?ということは後の記事で解説しますが、ちょっとだけ言及しておくと、
$$
\begin{pmatrix}
5&-4&6 \\
7&-6&10\\
4&9&7\\
\end{pmatrix}\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)
=\left(\begin{array}{c}
8\\
14\\
74
\end{array}\right)\quad\xrightarrow{うまーく変形すると…}
\begin{pmatrix}
1&0&0 \\
0&1&0\\
0&0&1\\
\end{pmatrix}\left(\begin{array}{c}
x\\
y\\
z
\end{array}\right)
=\left(\begin{array}{c}
2\\
5\\
3
\end{array}\right)
$$
となって、\((x,y,z)=(2,5,3)\)という解が導けます(後の記事で解説します)。
実は、この行列の変形は中学校で習った加減法に対応しています。
行列計算は機械学習の計算の核にもなっています。
つまり、機械学習の根本の部分は「行列の計算をしている」ということです。
で?行列とは何かネ?
では、「行列とは何か?」ということを説明します。
行列とは、一言で言ってしまえば
です。
これをもっとしっかり表すと次です。
行列、その成分、行と列
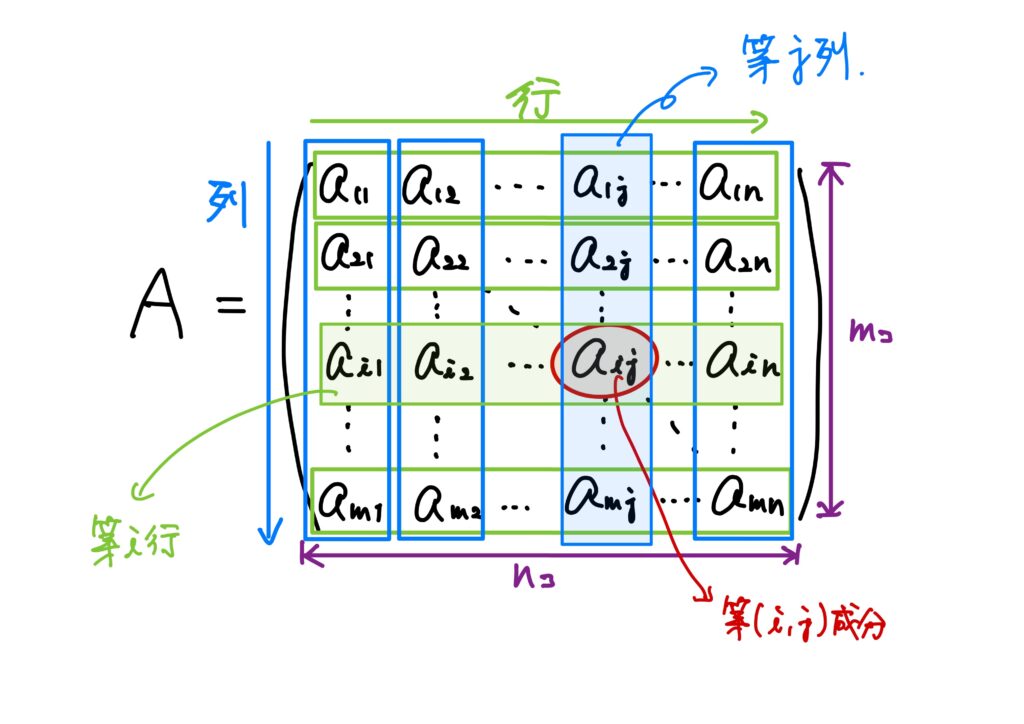
- 行列 自然数\(m,n\)に対して、\(mn\)個の複素数\(a_{ij}\ (1\leq i\leq m,1\leq j\leq n)\)を、縦\(m\)個、横\(n\)個の長方形に並べた表を、\((m,n)\)型の行列(matrix)、\((m,n)\)行列、または\(m\times n\)行列(\(m\)かける\(n\)ぎょうれつ)という。これを1つの大文字\(A\)で表し、 $$A= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1n}\\ a_{21}&a_{22}&\cdots &a_{2n}\\ \vdots&\vdots& \ddots&\vdots\\ a_{m1}&a_{m2}&\cdots &a_{mn}\\ \end{pmatrix} $$ と書く。
- 成分 行列を構成する\(mn\)個の数を行列の成分という。特に、上から\(i\)番目、左から\(j\)番目の位置にある成分\(a_{ij}\)を(第)\((i,j)\)成分という。
- 行と列 横一列に並んだ列を行といい、縦一列に並んだ列を列という。 特に、上から\(i\)番目の行を第\(i\)行、左から\(j\)番目の列を第\(j\)列という。
- 実行列 成分がすべて実数であるような行列、すなわち、\(1\leq i\leq m\)、および\(1\leq j\leq n\)を満たす任意の\(i,j\in\mathbb{N}\)に対して、\(a_{ij}\in\mathbb{R}\)であるような行列を実行列という。
各成分が\(a_{ij}\)であるような行列\(A\)を\(A=(a_{ij})\)と略記することもあります。
先程、行列を平たく言うと、「ベクトルをたくさん並べたものですよ〜」という話をしました。
上記の行列\(A\)において、\(m=1\)の場合および\(n=1\)の場合を考えるとスッとわかると思います。
行ベクトル、列ベクトル
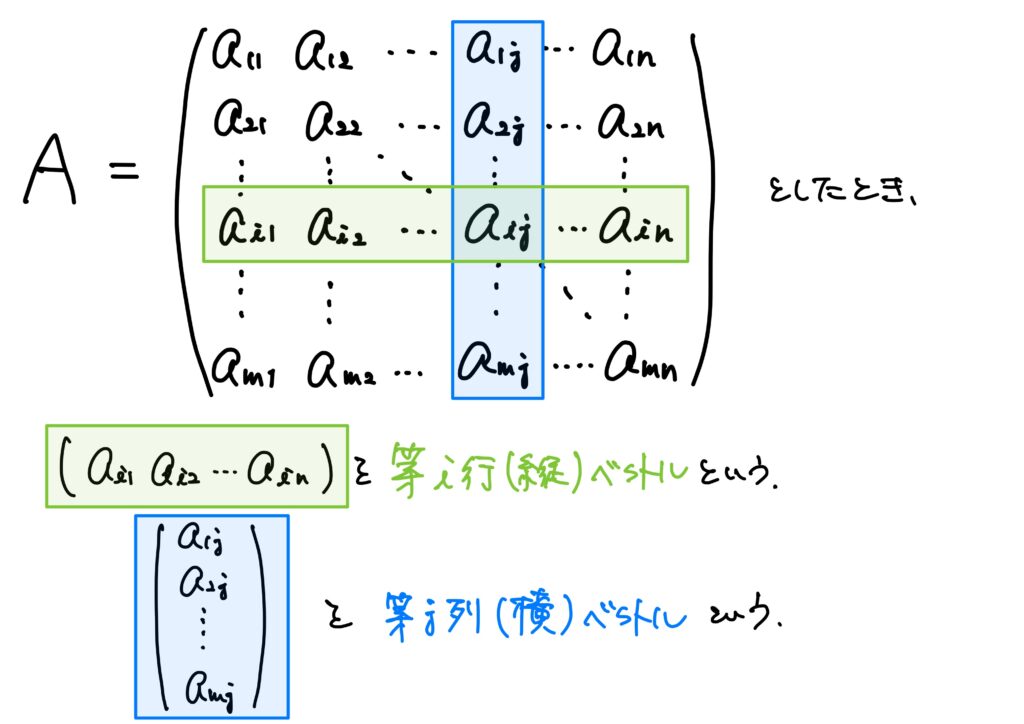
- 行ベクトル \((1,n)\)型の行列\(A=(a_{ij})\)を(\(n\)項)行ベクトル、あるいは(\(m\)項)横ベクトルという。行ベクトルは一般の行列特別するため、太い小文字で表現される。すなわち、 $$ \boldsymbol{a}=(a_1\ a_2\ \cdots\ a_n) $$ と書く。
- 列ベクトル \((m,1)\)型の行列\(A=(a_{ij})\)を(\(m\)項)列ベクトル、あるいは(\(m\)項)縦ベクトルという。列ベクトルも一般の行列特別するため、太い小文字で表現される。すなわち、 $$ \boldsymbol{b}=\left(\begin{array}{c} a_1\\ a_2\\ \vdots \\ a_m\end{array}\right) $$ と書く。
正直なところ、行ベクトルは限られた場合にしか使いません。
線型代数において、”ベクトル”と言った場合は基本的に列ベクトルのことを指します。
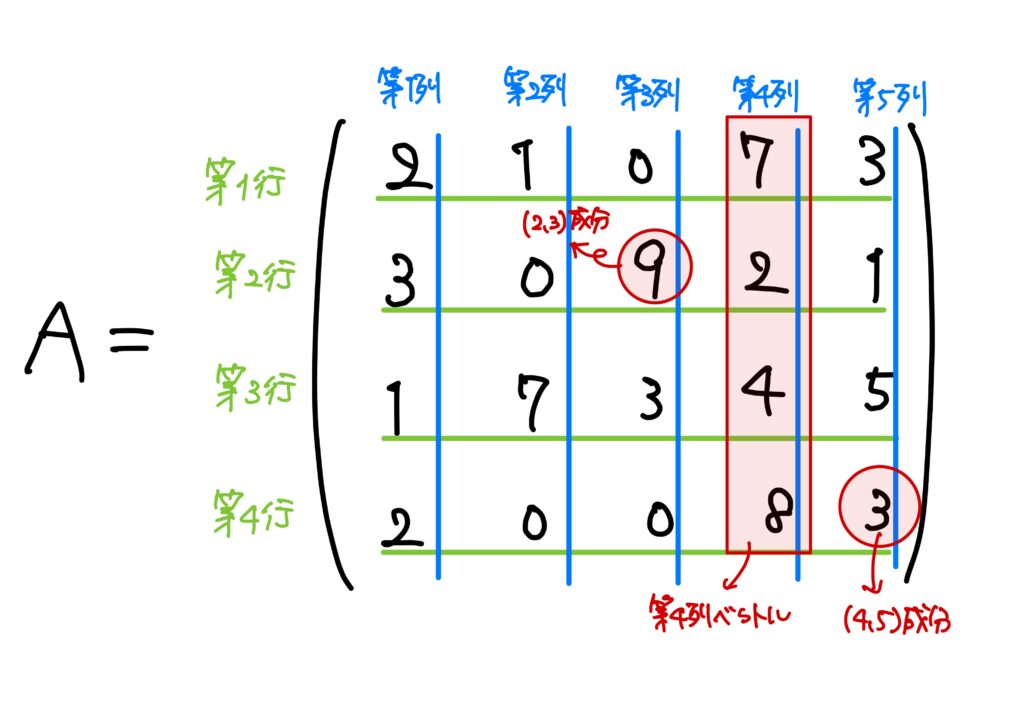
例1.次のような行列を考えてみます。
$$A=(a_{ij})=
\begin{pmatrix}
2&1&0&7&3\\
3&0&9&2&1\\
1&7&3&4&5\\
2&0&0&8&3\\
\end{pmatrix}
$$
に対して、
- \(A\)の\((2,3)\)成分\(a_{23}\)は、\(2\)行\(3\)列目の成分なので、\(a_{23}=9\)です。
- \(A\)の\((4,5)\)成分\(a_{45}\)は、\(4\)行\(5\)列目の成分なので、\(a_{23}=3\)です。
- 第\(3\)行ベクトルは\((1\ 7\ 3\ 4\ 5)\)です。
- 第\(4\)列ベクトルは\(\displaystyle\left(\begin{array}{c} 7\\2 \\4\\ 8\end{array}\right)\)です。
「なんか直感的じゃない?」と思うかもしれませんが、「行列とは何か?」という問にはこれでOKです。
本来はある性質を満たすものを行列と呼び、その性質こそ、今後記事として解説していく行列の性質です。
つまり、行列が満たすべき性質を満たす”モノ”はすべからく行列なのであり、その”モノ”を模式的に表したのが、上記のようにカッコでくくった行列です。
行列が等しいって?(行列の相等)
「行列が等しいってどういうことかネ?」という話です。
大方予想がついているかと思いますが、明言しておきます。
行列の相等
2つの行列\(A\)および\(B\)が等しいとは、\(A\)、\(B\)が同じ型の行列であって、対応する成分がすべて等しいことだと定め、これを\(A=B\)と表す。
すなわち、
$$
A=\begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots&\vdots& \ddots&\vdots\\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix},\quad B=\begin{pmatrix}b_{11}&b_{12}&\cdots &b_{1l}\\b_{21}&b_{22}&\cdots &b_{2l}\\\vdots&\vdots& \ddots&\vdots\\b_{k1}&b_{k2}&\cdots &b_{kl}\\\end{pmatrix}
$$
のとき、\(m=k\)、\(n=l\)であり、かつ
$$
(\forall i\in\mathbb{N}:1\leq i\leq m )(\forall j\in\mathbb{N}:1\leq j\leq n )\ a_{ij}=b_{ij}
$$
が成り立つとき、行列\(A\)および\(B\)は等しい、といい\(A=B\)で表す。
「そりゃそうじゃね?」といったところかと思いますが一応「こんなのは等しくない」という行列を述べておきます。
例2.
$$
A=\begin{pmatrix}
1&2&3 \\
4&5&6
\end{pmatrix},\quad
B=\begin{pmatrix}
1&2&3 &0\\
4&5&6 &0\\
0&0& 0&0\\
0&0&0 &0\\
\end{pmatrix}
$$
これらは成分が似ている(似ていると言っていいのかな…)わけですが、\(A\)は\((2,3)\)型、\(B\)は\((4,4)\)型と型が一致していないため等しくありません。
よく使われる行列
では、行列の中で特に代表的な行列を説明します。
それは
- 零行列(ぜろぎょうれつ)
- 正方行列
- 対角行列
- 単位行列
です。
零行列
簡単です。
すべての成分が\(0\)であるような行列を零行列といいます。
零行列 \((m,n)\)型の行列に対して、すべての成分が\(0\)であるような行列、すなわち、 $$ (\forall i\in\mathbb{N}:1\leq i\leq m )(\forall j\in\mathbb{N}:1\leq j\leq n )\ a_{ij}=0 $$ を満たす行列を零行列といい、\(O\)(アルファベットのオー)で表す。 $$O= \begin{pmatrix} 0&0&\cdots &0\\ 0&0&\cdots &0\\ \vdots&\vdots& \ddots&\vdots\\ 0&0&\cdots&0\\ \end{pmatrix} $$
ここで注意なのが、
ということです。
要は型が違っても成分がすべて\(0\)であればすなわち零行列です。
例えば、
$$
O_1=
\begin{pmatrix}
0& 0\\
0&0\\
\end{pmatrix},\quad
O_2=
\begin{pmatrix}
0& 0&0\\
0&0&0\\
0&0&0\\
0&0&0\\
\end{pmatrix}
$$
としたとき、\(O_1\)も\(O_2\)も零行列です。
正方行列
これも簡単です。
行列の形が正方形であるような行列です。
正確には以下です。
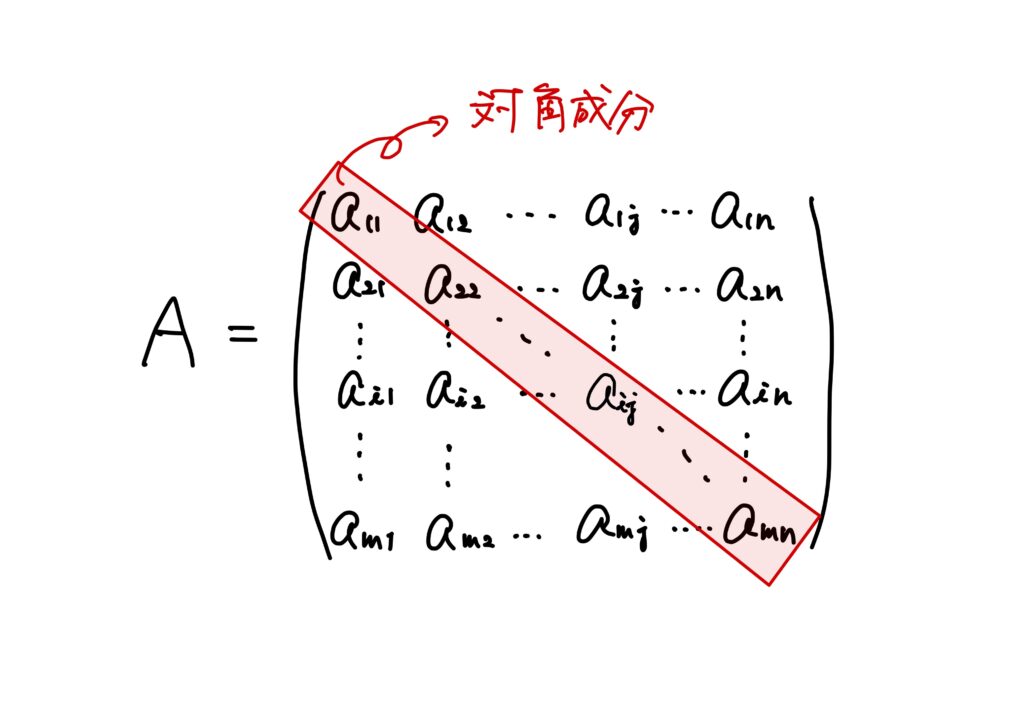
正方行列と対角成分
- 正方行列 \((m,m)\)型の行列を\(m\)次正方行列という。すなわち、 $$A= \begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1m}\\a_{21}&a_{22}&\cdots &a_{2m}\\\vdots&\vdots& \ddots&\vdots\\a_{m1}&a_{m2}&\cdots &a_{mm}\\\end{pmatrix} $$ を正方行列という。
- 対角成分 \(m\)次正方行列\(A=(a_{ij})\)に対して、第\((i,i)\)成分\(a_{ii}\ (1\leq i\leq m)\)を\(A\)の対角成分という。
これも零行列と同じで、自然数\(m\)に対して\(m\)次正方行列が定められます。
例えば、一番初めに連立一次方程式の係数行列として挙げた
$$
\begin{pmatrix}
5&-4&6 \\
7&-6&10\\
4&9&7\\
\end{pmatrix}
$$
は\(3\)次正方行列で、対角成分は\(5,-6,7\)です。
$$
\begin{pmatrix}
1& 2&3&4\\
5&6&7&8\\
9&10&11&12\\
13&14&15&16\\
\end{pmatrix}
$$
は\(4\)次正方行列で、対角成分は\(1,6,11,16\)です。
対角行列
これは正方行列の仲間です。
正方行列において、対角成分以外の成分が全部\(0\)である行列を対角行列といいます。
すなわち、以下です。
対角行列 \(m\)次正方行列\(A=(a_{ij})\)に対して、対角成分以外の成分がすべて\(0\)であるような行列、すなわち、 $$ (\forall i,j\in\mathbb{N}:1\leq i,j\leq m)\ (i\neq j\Rightarrow a_{ij}=0) $$ を満たすような行列を(\(m\)次)対角行列という。対角行列を成分で表示すれば、 $$A= \begin{pmatrix} a_{11}&0&\cdots &\cdots&0\\ 0&a_{22}&0 &\cdots&0\\ \vdots&0& \ddots&\ddots&\vdots\\ \vdots&\vdots& \ddots&\ddots&0\\ 0&\cdots&\cdots&0 &a_{mm}\\ \end{pmatrix} $$ となるとき、\(A\)は\(m\)次対角行列という。また、このとき、 $$A= \begin{pmatrix} a_{11}&&&&\\ &a_{22}&&\huge{0}& \\ &&\ddots&&\\ &\huge{0}&&\ddots&\\ &&&&a_{mm}\\ \end{pmatrix} $$ と書くこともある。
ここで、「対角成分以外が\(0\)」という表現はあまり良くないかもしれません。
というもの、「対角成分以外が\(0\)」という表現だと「対角行列の対角成分はすべて\(0\)じゃないってことか」というミスリードを誘導してしまうかもしれないからです。
「対角成分以外が\(0\)」ということなので、対角成分が何であるかには言及していません。
故に何でも良いわけです。
勿論\(0\)でもよいわけです。
そうなると、零行列\(O\)が正方行列だった場合、この\(O\)は対角行列となります。
単位行列
これはシンプルです。
対角成分がすべて\(1\)であるような対角行列を単位行列といいます。
単位行列
\(A=(a_{ij})\)を\(m\)次対角行列とする。このとき、
$$
\delta_{ij}=
\begin{cases}
1&(i=j)\\
0&(i\neq j)
\end{cases}
$$
としたとき(この\(\delta_{ij}\)をクロネッカー(Kronecker)の\(\delta\)という)、
$$
a_{ij}=\delta_{ij}
$$
を満たすとき、\(A\)は(\(m\)次)単位行列といい、\(I_m\)や\(E_m\)で表す。
すなわち、
$$I_m=E_m=
\begin{pmatrix}
1&&&&\\
&1&&\huge{0}& \\
&&\ddots&&\\
&\huge{0}&&\ddots&\\
&&&&1\\
\end{pmatrix}
$$
を(\(m\)次)単位行列という。
これは「ふーん」程度でよいのですが(後に分かるので)、単位行列\(I_m\)は実数の掛け算における\(1\)に対応します(詳しくは行列の演算の記事で)。
転置
転置もシンプルです。
要は、\((m,n)\)行列\(A=(a_{ij})\)の行と列を入れ替えた行列のことです。
行と列を入れ替えた行列は\((n,m)\)行列となり、その成分は\(a_{ji}\)となります。
転置行列 \((m,n)\)行列\(A=(a_{ij})\)に対して、行と列を入れ替えた行列を\(A\)の転置行列といい、\(A^\top\)や\(^t\!A\)で表す。 すなわち、\(A=(a_{ij})\)を $$ A= \begin{pmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots&\vdots& \ddots&\vdots\\a_{m1}&a_{m2}&\cdots &a_{mn}\\\end{pmatrix} $$ と書いたとき、\(^t\!A=(a_{ji})\)を、つまり $$^t\!A=A^\top= \begin{pmatrix} a_{11}&a_{12}&\cdots &a_{1m}\\ a_{21}&a_{22}&\cdots &a_{2m}\\ \vdots&\vdots& \ddots&\vdots\\ a_{n1}&a_{m2}&\cdots &a_{nm}\\ \end{pmatrix}$$ を\(A\)の転置行列という。
ちなみに、行列\(A\)の転置行列\(^t\!A\)の\(t\)はtransposeのtです。
筆者は大学初年度のとき「転置のローマ字のtから来てんのか〜」と勝手に思って恥ずかしかった記憶があります。
数学の記号は全部アルファベットなのにいきなり日本語が出てくるわけないのにね(笑)
簡単ではありますが、例を挙げておきます。
例3.
$$A=
\begin{pmatrix}
1&2\\
3&4\\
5&6\\
\end{pmatrix}
$$
としたとき、\(^t\!A\)は
$$
^t\!A=
\begin{pmatrix}
1&3&5\\
2&4&6\\
\end{pmatrix}
$$
です。
「こんな行と列を入れ替えただけの行列なんて何に使うんだ?」と思うかもしれませんが、直交行列を語るときに使います。
直交行列には強力な性質がありますので、そのときまでお楽しみに。
結
今回は「行列とは何か?」ということを皮切りに、行列の相等、零行列、正方行列、対角行列、単位行列、行列の転置について解説しました。
今回は特に何か主張を証明しようという話ではなく、これから行う線型代数学の勉強で必要な行列の呼び名だったりを解説しました。
次回は行列の演算です。
乞うご期待!質問、コメントなどお待ちしております!




コメントをする