「行列の既約性、有向グラフの強連結性②〜強連結成分〜」【幾何学の基礎シリーズ】グラフ理論編その6

本記事の内容
前回、今回、次回で言いたいこと
強連結成分を一言で。
その前に、部分グラフ
有向グラフの頂点の集合に「関係」を定めます。
1. 同値関係の軽い復習
2. 有向グラフの頂点の集合に同値関係を定めます。
頂点の集合 $V=\left\{1,\dots,n\right\}$ の分割と強連結成分
皆様のコメントを下さい！
結

本記事の内容

本記事は強連結成分について解説する記事です。

本記事を読むにあたり、有向グラフと強連結について知っている必要があるため、以下の記事も合わせてご覧ください。

前回、今回、次回で言いたいこと

前回、今回、次回で言いたいことは次の2つです。

定理0-1.

与えられた

n

$n$ 次の正方行列

A = (a_{i j})

$A=\left( a_{ij}\right)$ が可約であれば、添字の番号を並べ替えることにより、次の行列に変形することが出来る。

$\begin{pmatrix} A_1&\ast&\ast&\cdots&\ast\\ O&A_2&\ast&\cdots&\ast\\ \vdots&\ddots&\ddots&\ddots&\ast\\ O&\cdots&O&A_{s-1}&\ast\\ O&O&\cdots&O&A_s\\ \end{pmatrix}$ ただし、

$A_i$ は既約な正方行列である。

これは次回証明します。

定理0-2.

有向グラフが強連結であることと、有向グラフの隣接行列が既約であることは同値である。

この主張の十分性は前回証明しました。
必要性は次回証明します。

今回は、これらを示すために強連結成分について解説します。
(※ある種、次回の準備です。)

強連結成分を一言で。

強連結成分を一言で述べれば、

有向グラフにおいて、強連結な部分(一部の有向グラフ)のこと。

です。
実は、強連結成分とは何か？ということも大事ですが、それよりも

強連結でないグラフは、強連結成分(strongly connected component)に「分解」できる。

という事実が重要です。
ただし、この事実は「強連結でないグラフから強連結なグラフが作れる」と言っているわけではありません。

その前に、部分グラフ

と、説明する前に部分グラフについて解説します。
これは読んで字の如し、グラフの一部分のグラフ、という意味です。
これを数学的に書くと次です。

部分グラフ

グラフ

$X=(V,E)$ に対して、

$V_1\subset V$ 、

$E_1\subset E$ とする。このとき、

$i(E_1)\subset V_1\times V_1$ かつ

$\overline{E_1}=E_1$ であるとき、

$X_1=\left( V_1,E_1\right)$ はグラフである。このグラフ

$X_1$ を

$X$ の部分グラフといい、

$X_1\subset X$ と書く。

$i(E_1)\subset V_1\times V_1$ のミソはグラフ $X$ において存在する $i$ と同じ $i$ に対して、 $E_1\subset E$ の $i$ による順像が $V_1\times V_1$ の部分集合であるということです。
つまり、頂点 $V_1$ 繋がり方が、元々のグラフ $X$ との頂点 $V$ と同じ繋がり方をしていることを指しています。
$\overline{E_1}$ は無向グラフなので、この条件が必要です。

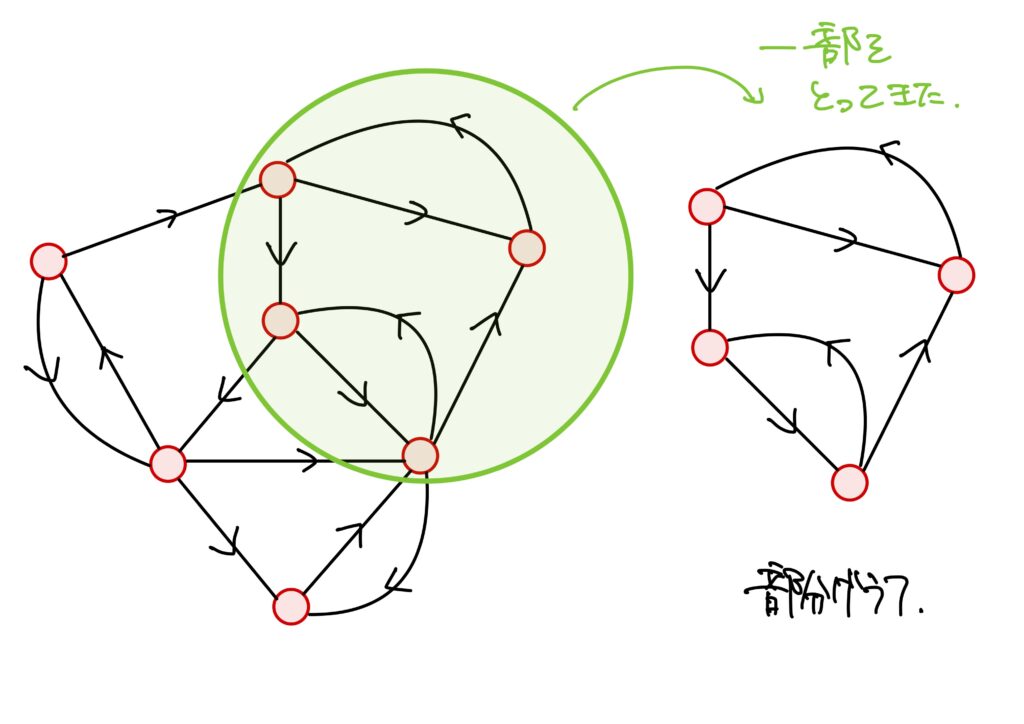
有向グラフの頂点の集合に「関係」を定めます。

先程「分解できる」という表現をしました。
「分解できる」は少し別の表現をすると「グループ分けすることができる」です。

ここで、「あ！あれだ！あれを使うんだ！」となってくださると嬉しいです。

答えは同値関係です。

同値関係の軽い復習

軽く同値関係を復習します。

同値関係

次の３条件を満たす集合

$X$ 上の関係

$\sim$ を同値関係(equivalence relation)という。

$x\in X$ のとき、 $x\sim x$ (反射律),
$x,y\in X$ のとき、 $x\sim y\Rightarrow y\sim x$ (対称律),
$x,y,z\in X$ のとき、 $x\sim y,\ y\sim z\Rightarrow x\sim z$ (推移律)

詳しくは、【論理と集合シリーズ】その7を御覧ください。

例えば、我々がよく使う $=$ は同値関係です。
しかし、 $<$ やら $>$ やら $\geq$ やら $\leq$ やらは同値関係ではありません。

同値関係の重要な性質の1つとして次があります。

定理1.

$x\in X$ と同値な要素全体を

$C_x$ と書き、これを

$x$ の同値類(equivalence class)という。すなわち、

$C_x=\{y\in X\mid x\sim y\}$ である。このとき、次が成り立つ。

$x\in C_x$ ,
$C_x\cap C_y\neq \emptyset \Rightarrow C_x=C_y$ ,
$C_x\neq C_y\Rightarrow C_x\cap C_y= \emptyset$ ,
$\displaystyle\bigcup_{x\in X}C_x=X$ ,
$x,y\in X,\ x\neq y,\ \Rightarrow\ C_x\cap C_y=\emptyset$

定理1.の証明は【論理と集合シリーズ】その7を御覧ください。

有向グラフの頂点の集合に同値関係を定めます。

「同値関係を定めます。」というのはあまり良い表現ではないかもしれません。
厳密には「有向グラフの頂点の集合に”うまく”関係を定めると、同値関係になる。」と表現すべきかもしれません。

さて、有向グラフの頂点の集合を $\left\{1,\dots,n\right\}$ として、頂点の集合に次のような関係 $\sim$ を定めます。

頂点の集合における関係

与えられた有向グラフの頂点の集合を

$V=\left\{1,\dots,n\right\}$ とし、任意の頂点

$i,j\in V$ に対して次の関係を定める。

$i\sim j\ \Longleftrightarrow\ i$ から

$j$ に向かう路と、

$j$ から

$i$ に向かう路が存在する。

ただし、全ての頂点

$i$ に対して、

$i\sim i$ とする。

つまり、 $i$ から辺をたどって $j$ にたどり着く路と、 $j$ から辺をたどって $i$ たどり着く路の双方が存在するときに「頂点 $i$ と頂点 $j$ には”関係がある”と言い、このときを $i\sim j$ で表す。」というわけです。

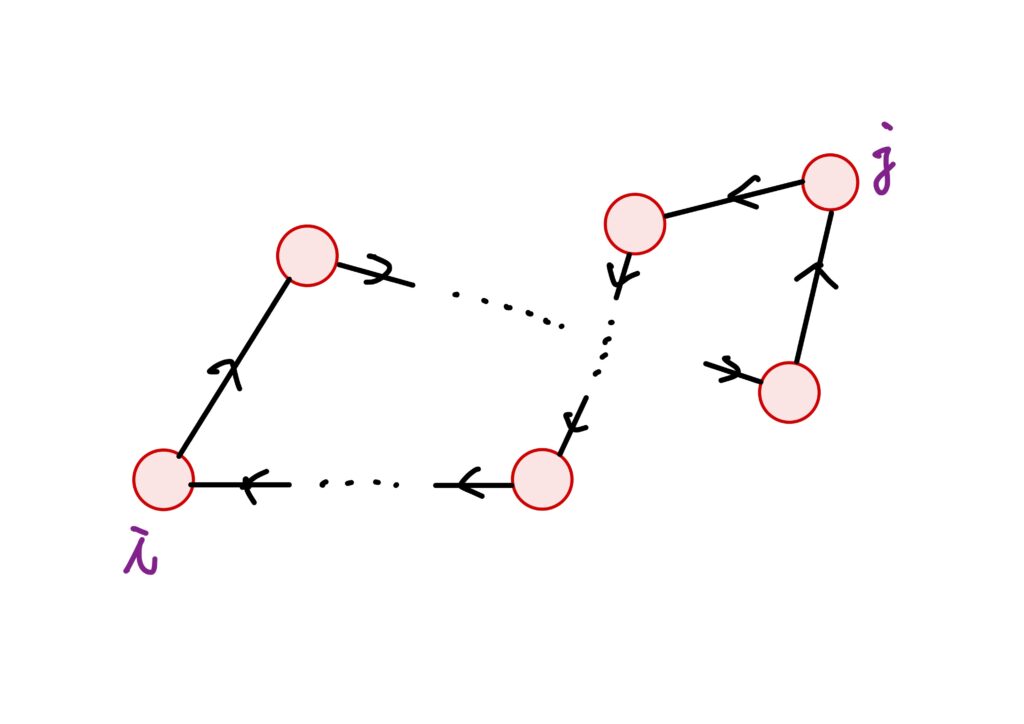
※注意※ 上記のように書くと、「 $\sim$ と書いたらば $i$ から $j$ に向かう路と、 $j$ から $i$ に向かう路が存在することを表している」と捉えられるかもしれませんがそうではありません。
あくまでここでは $\sim$ を上記のように定める、という話です。

さて、先程定めた関係 $\sim$ は実は同値関係です。

命題2.

与えられた有向グラフの頂点の集合を

$V=\left\{1,\dots,n\right\}$ とし、任意の頂点

$i,j\in V$ に対して定めた

$i\sim j\ \Longleftrightarrow\ i$ から

$j$ に向かう路と、

$j$ から

$i$ に向かう路が存在する。

かつ

$\forall i\in V$ に対して

$i\sim i$ という関係

$\sim$ は同値関係である。

これは同値関係の良い復習になると思われますので、是非一度証明してみて下さい。

命題2.の証明

何を示せばよいかというと、以下の3つです。

反射律： $i\in V$ のとき、 $i\sim i$ である。
対称律： $i,j\in V$ のとき、 $i\sim j\Rightarrow j\sim i$ である。
推移律： $x,y,z\in X$ のとき、 $i\sim j,\ j\sim k\Rightarrow i\sim k$ である。

①反射律の証明

これは、そもそも関係 $\sim$ の定め方で $\forall i\in V$ に対して $i\sim i$ としたので、成り立っています。

②対称律の証明

$i,j\in V$ が $i\sim j$ であるとします。
このとき、関係 $\sim$ の定め方から、頂点 $i$ から頂点 $j$ に向かう路 $c$ と頂点 $j$ から頂点 $i$ への路 $c^\prime$ が存在するので、 $j\sim i$ です。

③推移律の証明

任意の $i,j,k\in V$ に対して、 $i\sim j$ かつ $j\sim k$ であるとします。
すなわち、頂点 $i$ から頂点 $j$ に向かう路 $c_1$ と頂点 $j$ から頂点 $k$ に向かう路 $c_2$ が存在します。
すなわち、 $i=o(c_1)$ かつ $j=t(c_1)=o(c_2)$ かつ $k=t(c_2)$ という路 $c_1,c_2$ が存在します。
故に、路 $c_1$ と路 $c_2$ をつなげてできる辺の列 $c_1\cdot c_2$ は、頂点 $i$ から頂点 $k$ に向かう路となっています。
より正確には、 $i=o(c_1)$ かつ $j=t(c_1)=o(c_2)$ かつ $k=t(c_2)$ という路 $c_1,c_2$ をそれぞれ $c_1=(e_1,\dots,e_n)$ 、 $c_2=(e^\prime_1,\dots,e^\prime_m)$ と書いたとき、
$c_1\cdot c_2=\left( e_1,\dots,e_n,\ e^\prime_1,\dots,e^\prime_m\right)$
は $o(e_1)=i$ かつ $t(e^\prime_m)=k$ となっているため、 $c_1\cdot c_2$ は頂点 $i$ を始点、頂点 $k$ を終点とする路です。

次に、 $i\sim j$ かつ $j\sim k$ だから、頂点 $j$ から頂点 $i$ に向かう路 $d_1$ と頂点 $k$ から頂点 $j$ に向かう路 $d_2$ が存在します。
これも先程と同様にして $d_2\cdot d_1$ は始点を $k$ 、終点を $i$ とする路です。
従って、推移律が成り立ちます。

命題2.の証明終わり

これで晴れて先程定めた頂点の集合 $V=\left\{1,\dots,n\right\}$ 上の関係 $\sim$ は同値関係であることが示されました。

先程定めたこの関係 $\sim$ は同値関係ですので、定理1.から $V$ を分割すること出来ます。

頂点の集合 $V=\left\{1,\dots,n\right\}$ の分割と強連結成分

$V$ の分割

さて、先程定めた関係 $\sim$ は同値関係ですので、定理1.から $V$ を次のように分割することが出来ます。
$V=V_1\cup V_2\cup\cdots\cup V_s$
だたし、各 $V_a$ は、その中の2頂点 $i,j$ に対して $i\sim j$ が成り立ち、しかもこの性質を持つ最大のものです。
要するに、各 $V_a$ は関係 $\sim$ による同値類です。
各 $V_a$ は同値類ですから、任意の $1\leq p,q\leq s$ を満たす自然数 $p,q$ に対して、 $V_p\cap V_q=\emptyset$ であることに注意です。

強連結成分

各 $V_a$ に対して、 $V_a$ の2頂点を結ぶ路上にある辺を全て集めて、 $V_a$ を頂点の集まりとする有向グラフを作ります。
このグラフを $X_\alpha^o$ で表すことにしましょう。
たとえは次のようなグラフです。

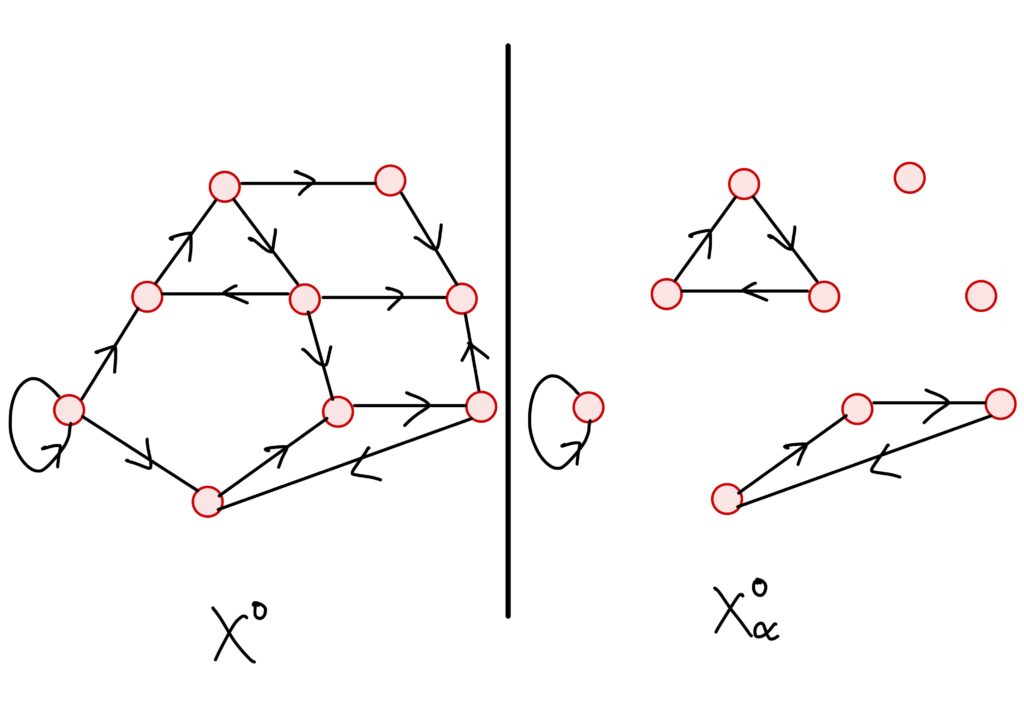
このようにして得られる有向グラフたちは強連結であり、元の有向グラフの強連結成分と呼ばれます。
ここで「お？ということは強連結成分は部分グラフなのね。」となってくれると嬉しいです。

つまり、以下です。

強連結成分

有向グラフ

$X^o$ の強連結な部分グラフ

$X_1^o$ を

$X^o$ の強連結成分という。

要するに、強連結な部分は、どの頂点からもどの頂点への路が存在するので、強連結な部分は1頂点と捉えてしまおう、というお話です。
これはまさに、最初に述べた

強連結でないグラフは、強連結成分(strongly connected component)に「分解」できる。

を表しています。

各強連結成分を1つの頂点と考え、更に強連結成分に属さない辺でそれらを結ぶことで、新しい有向グラフが得られます。

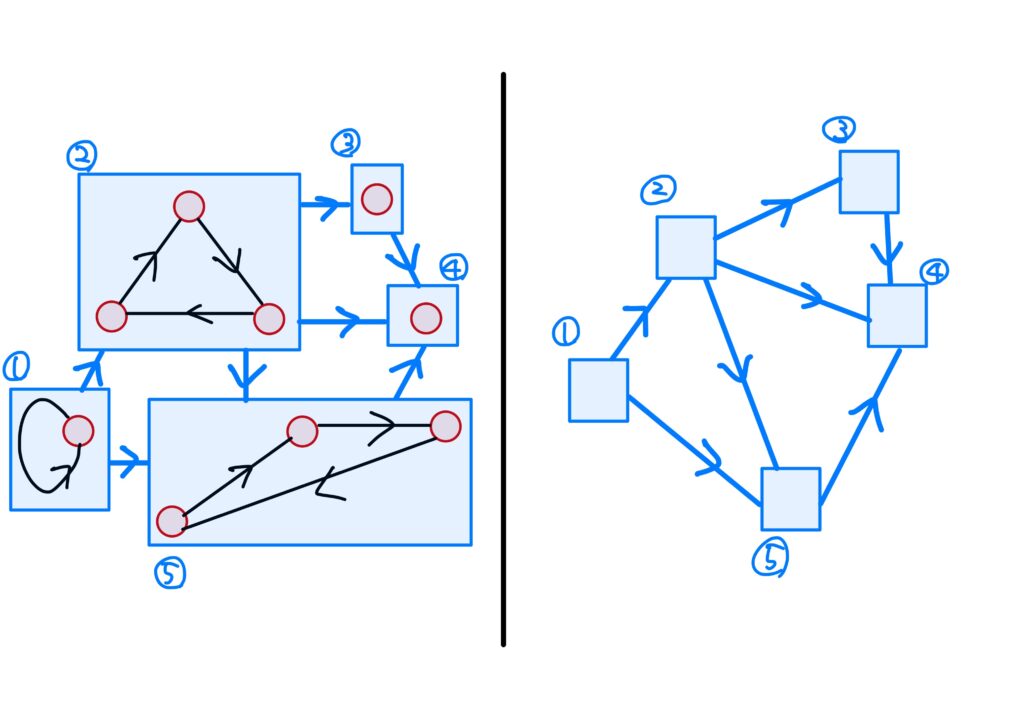
これを $X_{new}^o$ で表しましょう。
この新しいグラフ $X_{new}^o$ は「始点と終点が一致する路(閉路)は存在しない」という性質を持っています。

命題3.

$X_{new}^o$ には閉路が存在しない。

命題3.の証明

背理法で証明します。
仮に $X_{new}^o$ に閉路が存在するとします。
その上には $X_{new}^o$ の2頂点、例えば $V_a$ 、 $V_b$ が存在します。
閉路を使えば、 $V_a$ に属する元のグラフ $X^o$ の頂点から $V_b$ の頂点への路が存在します。
逆に、 $V_b$ に属する頂点から $V_b$ の頂点の路が存在します。

$V_a$ と $V_b$ が強連結であることを使えば、 $V_a$ の頂点 $i$ と $V_b$ の頂点 $j$ について $i\sim j$ が成り立つことになります。
これは矛盾です。

命題3.の証明終わり

$V_1,\dots,V_s$ の順序

次に、 $V_1,\dots,V_s$ に次のような関係 $\leq$ を導入します(ある種の大小関係のようなものです)。

$V_1,\dots,V_s$ の順序

$\displaystyle V_a\leq V_b\ \Longleftrightarrow\ V_a=V_b$ か、または

$V_a$ を始点とし

$V_b$ を終点とする新しいグラフでの路が存在する。

この関係は次の性質を満たしています。

$V_a\leq V_a$
関係 $\leq$ の定め方から、 $V_a=V_a$ のため、成り立ちます。
$V_a\leq V_b,\ V_b\leq V_a\ \Rightarrow\ V_a=V_b$
$V_a\leq V_b,\ V_b\leq V_a$ だとしましょう。
このとき $V_a$ を始点として $V_b$ を終点とする新しいグラフでの路 $c_1$ が存在し、かつ $V_b$ を始点として $V_a$ を終点とする新しいグラフでの路 $c_2$ が存在します。
つまり $V_a$ の任意の頂点から $V_b$ の任意の頂点への路が存在し、同時に $V_b$ の任意の頂点から $V_a$ の任意の頂点への路が存在するため、 $V_a\cup V_b$ を頂点の集合とする元のグラフの一部は強連結です。
すなわち、今、 $V_a$ と $V_b$ の要素を頂点とする元のグラフはそれぞれ強連結なため $V_a\cup V_b$ は強連結成分の頂点の集合です。
故に、 $V_a\subset V_b$ かつ $V_b\subset V_a$ なので $V_a=V_b$ です。
$V_a\leq V_b,\ V_b\leq V_c\ \Rightarrow\ V_a\leq V_c$
$V_a\leq V_b,\ V_b\leq V_c$ とします。
$V_a=V_b$ であれば、 $V_a=V_b\leq V_c$ となるので成り立ちます。
$V_b=V_c$ の場合も同様です。
次に、 $V_a$ 、 $V_b$ 、 $V_c$ のどれもが互いに等しくない場合を考えます。
このとき、 $V_a$ を始点とし $V_b$ を終点とする新しいグラフでの路 $c_1$ が存在し、かつ $V_b$ を始点とし $V_c$ を終点とする新しいグラフでの路 $c_2$ が存在します。
故に、 $c_1$ と $c_2$ をつなげて出来る $c_3=c_1\cdot c_2$ は $V_a$ の要素を始点、 $V_c$ の要素を終点とする路です。
従って、 $V_a\leq V_c$ です。

性質2.は「始点と終点が一致する路(閉路)は存在しない」ということを表現しています。

$V_a\leq V_b$ で、かつ $V_a\neq V_b$ であるとき、 $V_a<V_b$ と書くことにしましょう。
先程定めた関係 $\leq$ は数の大小関係と似ていますが、数の場合と違って、全ての $V_a,\ V_b$ に大小関係があるとはかぎりません。

余談(順序集合)

一般の集合において、その要素たちの関係

$\leq$ が次の性質を満たすとき、

$\leq$ を順序関係といい、順序関係の与えられた集合を順序集合と言います。

$x\leq x$ ,
$x\leq y,\ y\leq x\ \Rightarrow\ x=y$ ,
$x\leq y,\ y\leq z\ \Rightarrow\ x\leq z$ .

$V_a$ たちの番号付けと $V_a$ の中の頂点の番号付け

頂点に番号を付けます。

$V_a$ たちの番号付け

$V_a$ たちに次の規則で番号を付けます。

$V_b<V_a$ となる $V_b$ が存在しないような $V_a$ を選び(複数あるかもしれません)、これを極小元といい、これに番号 $1$ を付ける。
複数ある場合は一方を任意に選び番号 $1$ を付ける。
$V_a$ を取り除いたものの中で、極小元を選び、それに番号 $2$ を付ける。
この操作を繰り返す。

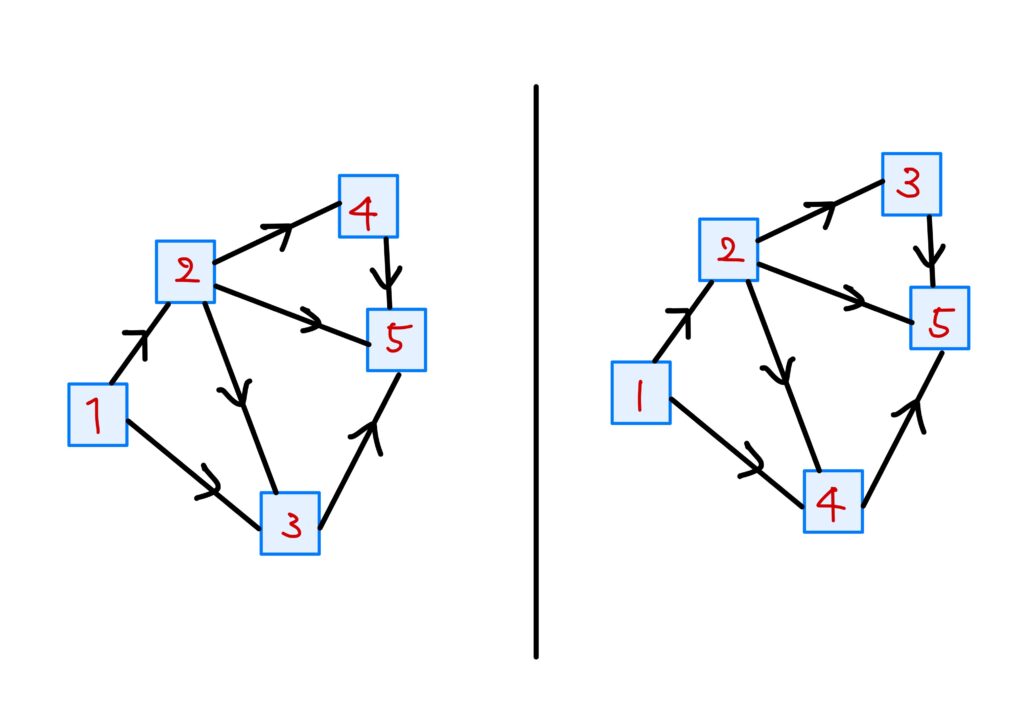
この番号付けと、先程定めた $\left\{V_a\right\}$ の順序関係 $\leq$ は次のように関連しています。

$V_a$ の番号が

$i$ 、

$V_b$ の番号が

$j$ であるとき、

$V_a\leq V_b$ ならば、
数の大小関係として

$i\leq j$ が成り立つ(逆は一般に成り立たない)。

そこで、 $V_a$ の番号が $i$ であるときに、改めて $V_a$ を $V_i$ と書くことにしましょう。
先程述べた通り、数として $i<j$ であるとき、 $V_j$ から $V_i$ への路は存在しません。
実際、もし $V_j$ から $V_i$ への路が存在したとすると、番号の付け方から、 $j\leq i$ となってしまうから矛盾です。

$V_a$ の中の頂点の番号付け

さらに、各 $V_i$ の頂点の数を $n_i$ として表し、 $V_i$ の頂点にも次の規則で番号付けします。

$V_1$ の頂点には、 $1,2,\dots,n_1$ の番号
$V_2$ の頂点には、 $n_1+1,n_1+2,\dots,n_1+n_2$ の番号
$\vdots$
以下同様にして、 $V_s$ の頂点には $n_1+\cdots+n_{s-1}+1,\ n_1+\cdots+n_{s-1}+2,\dots ,\ n_1+\cdots+n_{s-1}+n_s=n$ の番号

を付けます。

こうして、元々の有向グラフ $X^o$ の頂点に新しい番号が付けられました。
そこで、新しい番号 $k$ を持つ頂点の要素の番号が $i_k$ だったとして、置換 $\sigma$ を
$\sigma= \left(\begin{array}{c} 1&2&\cdots&n\\ i_1&i_2&\cdots&i_n\\ \end{array}\right)$
で定めます。

ちなみに、置換というのは以下でした。

置換

$n\in\mathbb{N}$ とする。

$n$ 個の文字

$1,2,\dots,n$ からなる集合を

$M_n=\{1,2,\dots,n\}$ とする。写像

$\sigma:M_n\to M_n$ が全単射であるとき、

$\sigma$ を

$M_n$ の置換という。
　置換

$\sigma$ による対応が

$1\mapsto i_1,\ 2\mapsto i_2,\dots,n\mapsto i_n$ であるとする、すなわち、

$\sigma(1)=i_1,\ \sigma(2)=i_2,\dots,\ \sigma(n)=i_n$ とする。このとき

$\sigma$ を

$\sigma= \begin{pmatrix} 1&2&\cdots&n \\ i_1&i_2&\cdots&i_n\\ \end{pmatrix}$ と書く。

詳しくは、【線型代数学の基礎シリーズ】行列式編その1を御覧ください。

皆様のコメントを下さい！

今回も数学者ジョークを1つ紹介します。

Aさん「数学者は何故国立公園が好きなの？」
数学者「天然の丸太(natural log=自然対数)があるからだよ。」

logは”丸太”という意味もあるので、こういうジョークが出来たようです。

皆様は他に数学者のジョークをご存知ですか？
是非コメントで教えて下さい！

結

今回は強連結成分について解説しました。
今回の記事は強連結成分について述べたもの、特に目新しいものはなかったと思います。
ある種、次回の準備です。

さて、強連結成分というのは、強連結でないグラフを強連結な部分とそうでない部分にわけ、強連結な部分(部分グラフ)を強連結成分と呼びます。

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34