本記事の内容
本記事は関数の収束のイメージを伝える記事である。
この記事を読むにあたり、数列の収束について知っているとより理解が深まると思われるので、その際は以下の記事を参照してください。
また、記法については写像の記事を見ていただけると良いと思われますので、次の記事もご参照ください。
記号のお話
\(I\subset\mathbb{R}\)を\(\mathbb{R}\)の区間とする。
この\(I\)に対して、\(\bar{I}\)は\(\mathbb{R}\)の区間\(I\)の端点を含んだ区間である。
つまり、\(I=(\alpha,\beta),\ (\alpha,\beta],\ [\alpha,\beta),\ [\alpha,\beta]\)の場合、\(\bar{I}=[\alpha,\beta]\)ということである。
ただし、\(I\)は必ずしも有界でなくても良い。
\(I=(\alpha,\infty),\ [\alpha,\infty)\)のときは\(\bar{I}=[\alpha,\infty)\)であり、\(I=(-\infty,\beta),\ (-\infty,\beta]\)のときは\(\bar{I}=(-\infty,\beta]\)である。
\(I=(-\infty,\infty)=\mathbb{R}\)の場合は\(\bar{I}=(-\infty,\infty)=\mathbb{R}\)である。
\(a\in I\)でなく\(a\in\bar{I}\)とする理由は別記事で書きます。
関数に対する収束
数列の収束との視点の違い
序を読んでいただいた方は「ん?数列の極限とは一味違うんじゃないか?」と思ったかもしれない。
実際そのとおりである。
数列の極限は「番号がどんどん大きくなっていくとき、数列の値はどの値に近づく、または近づかずに発散するのか」という話だった一方で、関数の極限は「\(x\)が定義域とその端点を含んだ区間の中の点に近づいたとき、関数はどの値に近づく、または発散するのか」ということだからである。
つまり、数列の極限は「最終的に値はどうなるの?」ということに興味があるのに対し、関数の極限は「この点で値はどうなるの?」ということに興味がある。
正確ではないかもしれないが、数列の極限は大域的に、関数の極限は局所的に考える、というわけである。
勿論、関数の極限でも大域的に、つまり「最終的に値はどうなるの?」ということも考えるが、どちらかというと局所的に、つまり「この点で値はどうなるの?」ということに興味がある。
なぜなのか、は次回または次次回の単元で説明する。

実関数の収束のイメージ(例と共に)
さて、数列と関数の極限に対する視点の違いが分かったところで、高校数学の復習がてら簡単な極限の例を見てみよう。
例1.
\(I_1=[0,5]\subset\mathbb{R}\)とし、\(f:I_1\to\mathbb{R}\)を\(f(x)=x^2\)で定めたとする。
つまりは、二次関数で定義域を\([0,5]\)に絞った関数である。
このとき、\(x\in I\)が\(3\in I_1\)に近づいたときの\(f\)の値\(f(x)\)はどうなっているかを考えてみよう。
高校数学で数Ⅲ(今はもう違う名前かもしれない)を学んだ方は「そりゃ\(9\)っしょ。」と思うだろう。
正しいです。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to3}f(x)=9\)というわけである。

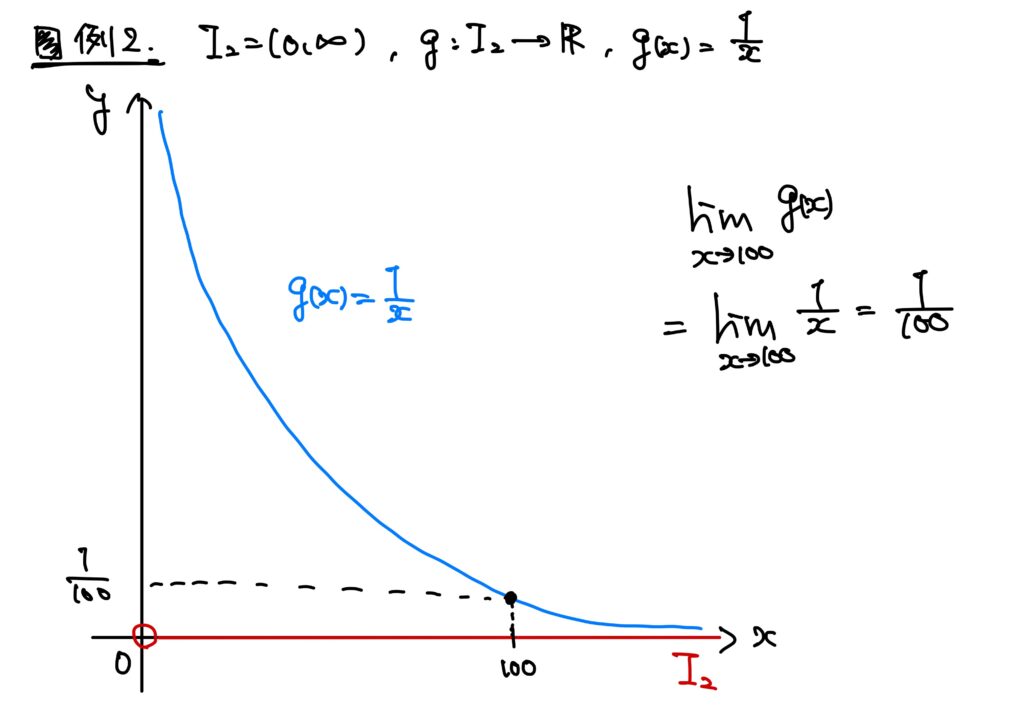
例2.
\(I_2=(0,\infty)=\mathbb{R}_{>0}=\{x\in\mathbb{R}\mid x>0\}\subset\mathbb{R}\)とし、\(g:I_2\to\mathbb{R}\)を\(g(x)=\displaystyle\frac{1}{x}\)で定めたとする。
つまりは、反比例で定義域を正の実数に絞った関数である。
このとき、\(x\in I_2\)が\(100\in I_2\)に近づいたときの\(g\)の値\(g(x)\)はどうなっているかを考えてみよう。
高校数学で数Ⅲを学んだ方は「そりゃ\(\displaystyle\frac{1}{100}\)っしょ。」と思うだろう。
正しいです。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to100}g(x)=\frac{1}{100}\)というわけである。
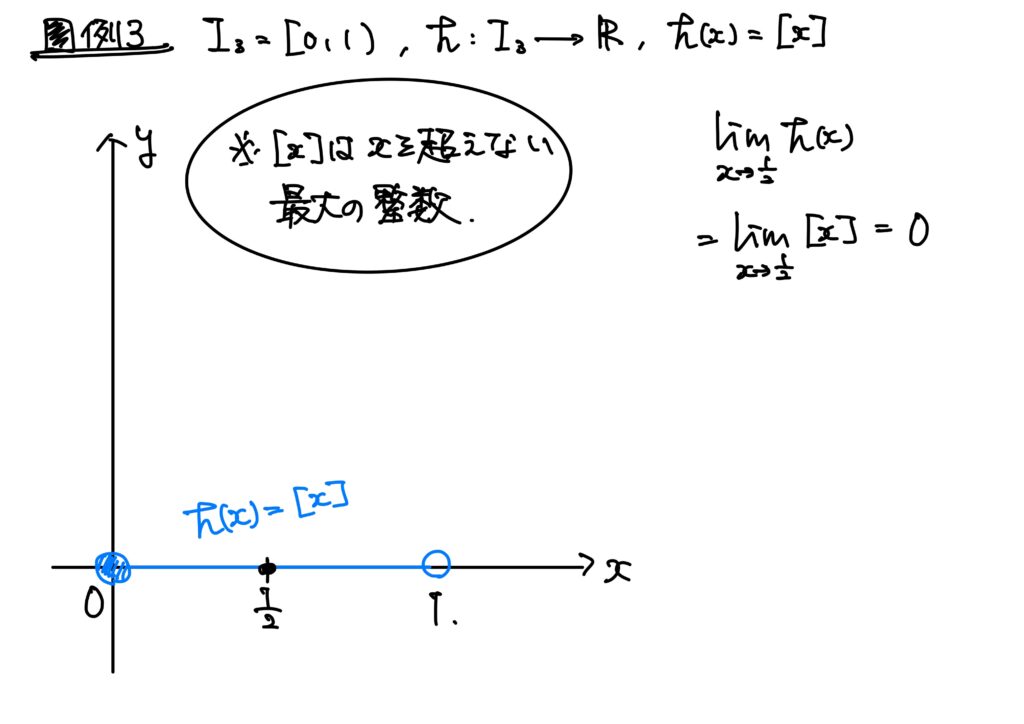
例3.(ガウス記号)
\(I_3=[0,1)\)とし、\(h:I_3\to\mathbb{R}\)を\(h(x)=[x]\)で定めたとする。
ただし、\([x]\)は\(x\)を超えない最大の整数である。
このとき、\(x\in I_3\)が\(\displaystyle\frac{1}{2}\in I_3\)に近づいたときの\(h\)の値\(h(x)\)はどうなっているかを考えてみよう。
答えは\(0\)である。
これを高校数学の記法で書けば、\(\displaystyle \lim_{x\to\frac{1}{2}}h(x)=0\)というわけである。
実関数の収束のイメージ(どう捉えられるか)
数列の収束は「ある番号以降はある値と十分近い」ということが収束のイメージだった。
しかし、実関数は序でも述べたとおり局所的な考え方をするので、まったくもって同じイメージというわけではない。
これにより「おや?分からねえぞ?」となるのではないか。
とはいえ、似ている部分も大いにある。
それについて説明する。
まず、関数の収束の直感的なイメージを1行で述べれば、結局の所
ということである。
少々記号を用いて書けば、関数\(f:I\to\mathbb{R}\)に対して、
ということである。
数列のときを思い出してみると、先の主張の後半の「\(f(x)\)が\(A\)に十分近づく。」は、「任意の正の実数\(\epsilon\)に対して、\(|f(x)-A|<\epsilon\)が成り立つことなんだな。」、つまり
$$(\forall \epsilon>0)\ |f(x)-A|<\epsilon$$
が成り立つことなんだな、と分かっていただけると思う。
では、前半の「\(x\in I\)が\(a\in\bar{I}\)に近づいたとき」について説明する。
これを論理的に捉えるために数列の話を思い出す。
数列は「ある番号以降の数列の値がとある値と十分近いときに収束するという。」のだった。
関数の収束については「\(a\in\bar{I}\)が含まれるとある区間内に入っている\(x\in I\)については、」と言い換えるのである。
「は?」と思うかもしれないので、前後半まとめて書くとわかりやすくなると思われる。
とどのつまり、関数の収束というのは、「\(x\in I\)と\(a\in\bar{I}\)の距離がある値(すなわち、距離)以内であれば、\(f(x)\)と\(A\)の距離\(|f(x)-A|\)が十分小さい。」ということである。
すなわち、
ということである。
数列は「ある番号以降は十分近い。」だったのに対し、関数は「とある範囲内であれば、十分近い。」ということが違いである。
従って、
というわけである。
結
今回は関数の収束についてのイメージを説明した。
要するに、関数の収束というのは
ということである。
数列の収束との視点の違いとしては、数列が「最終的にどうなるか」という大域的な視点に対して、関数は「この点ではどうなっているか」という局所的な視点である。
とはいえ、関数は大域的に考えないわけではない。
しかし、数列と違って局所的に考える理由は「連続」(グラフがつながっている)という概念が関数には存在するからである。
次回は数学的に関数の収束について述べ、簡単な例を証明する。





コメントをする