コーシー列のイメージをつかもう！

本記事の内容

本記事はコーシー列のイメージを説明する記事です。

本記事は数列の収束と密接に関係しているため、以下の数列の収束の記事も合わせてご覧ください。

数列の収束って？〜直感から論理へ〜

...

for-spring.com

2022.03.07

コーシー列の直感的な理解

前回の記事(【解析学の基礎シリーズ】実数の連続性編 その15)の余談その2で述べたことを掻い摘んでもう一度述べます。

「数列が収束するとは？」という条件を別の視点から言い換えてみます。
数列$\{a_n\}_{n\in\mathbb{N}}$が$a\in\mathbb{R}$に収束するというのは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-a|<\epsilon)$$
が成り立つということでした。
これは今まで、直感的には

ということだ、と説明してきました。
しかし、言い方を変えてみると、

とも言えるのです。
どういうことかと言うと、「ある番号$N$以降は全部$|a_n-a|<\epsilon$が成り立つ」のだから、その番号までは、すなわち$N-1$番目までは$|a_n-a|\geq\epsilon$が成り立つということです。
つまり、$|a_n-a|\geq\epsilon$が成り立つような$a_n$は$N-1$個しか無いのだから有限個しか存在しないのです。
より直感的に言えば、

ということなのです。

これを更に言い換えてみれば、収束する数列は

です。
この発想から得られた概念がコーシー列なのです。
この発想の立場に立ってみれば、「コーシー列も収束するんじゃね？」という意識もあまり抵抗がないのではないかと思われます。

結

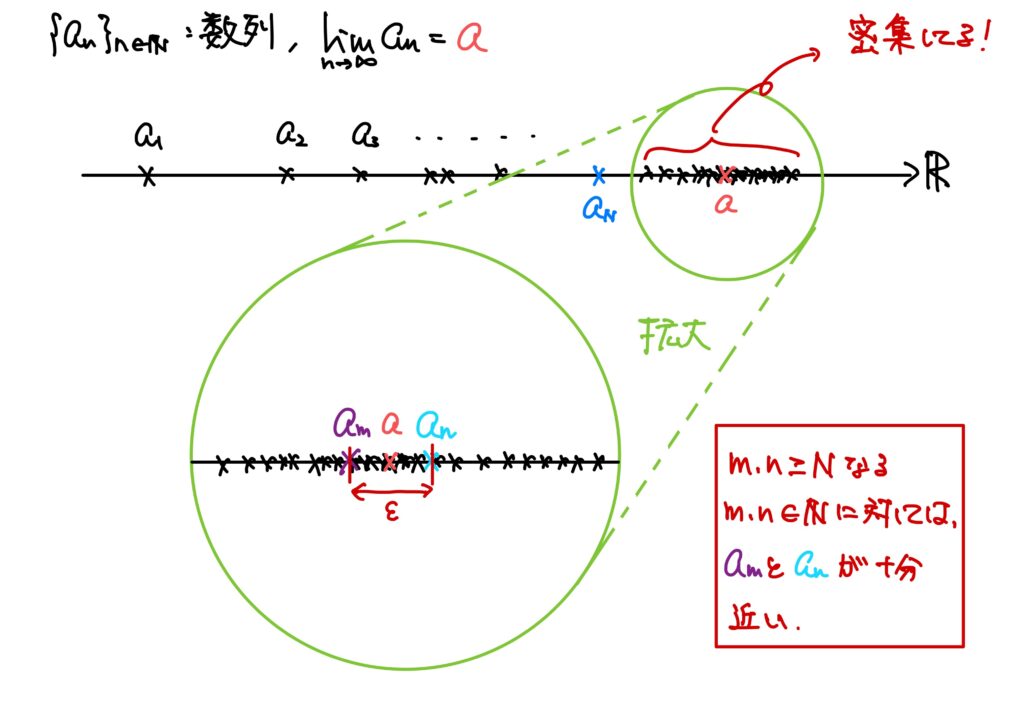
今回はコーシー列のイメージを説明しました。

一言で言えば、「ある番号以降の数列の値同士は十分近いのだ」ということです。

次回は「コーシー列ってどんなの？」という題でどのような数列がコーシー列なのかということの例とその証明を与えます。

乞うご期待！質問、コメントなどお待ちしております！