区間縮小法(区間縮小の原理)の証明

本記事の内容
区間縮小法(区間縮小の原理)のイメージの復習
区間縮小法(区間縮小の原理)の証明
結

本記事の内容

本記事は区間縮小法(区間縮小の原理とも)を「有界な単調列は収束する。」という命題から証明する記事です。

本記事を読むにあたり、「有界な単調列って収束する。」ということを知っている必要があるため、以下の記事も合わせてご覧ください。

区間縮小法(区間縮小の原理)のイメージの復習

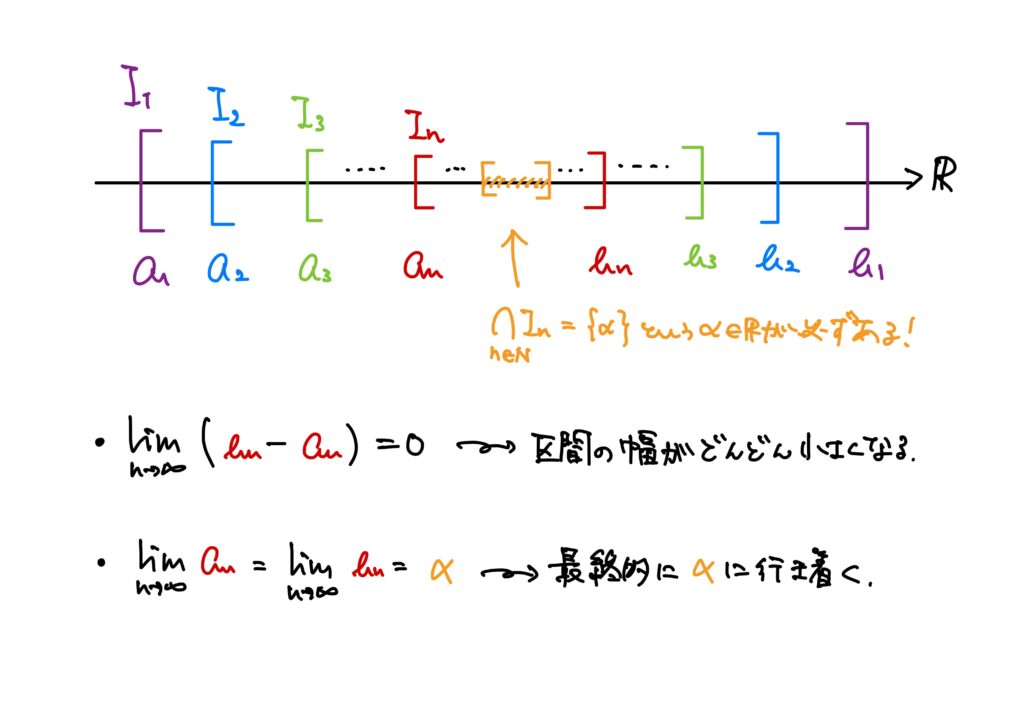
区間縮小の原理を一言で述べれば、

だんだん小さくなっていく有界な閉区間が無限に続くとき、その共通部分は1点のみからなる集合だ。

でした。
さらに、この区間縮小の原理が実数の数直線上のどんな有界な閉区間の列に対しても成り立つのだから、

実数の数直線上には一切”すき間”が無い。

ということがわかり、実数の連続性と関連があります。
詳しくは次回解説します。

↓実数の連続性との関連の記事

区間縮小法(区間縮小の原理)の証明

区間縮小法とはどういう主張なのかを数学的に明示します。
区間縮小法はしばしば区間縮小法の原理とも呼ばれます。
というのも、解析学の中で基本的な事実だからです。
ただし、この基本的というのは簡単という意味ではなく、議論をする上で元になる概念だ、という意味です。

区間縮小法(区間縮小の原理) $\{I_n\}_{n\in\mathbb{N}}$を縮小するような$\mathbb{R}$の有界な閉区間の列とする。すなわち、任意の$n\in\mathbb{N}$に対して、$I_n$は$\mathbb{R}$の閉区間で $$I_1\supset I_2\supset \dots I_n\supset I_{n+1}\supset\dots$$ を満たすとする。このとき、次が成り立つ。

任意の$I_n$に含まれる実数が存在する。すなわち $$\bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$$,
特に、$I_n=[a_n,b_n]$として、$\displaystyle \lim_{n\to\infty}(b_n-a_n)=0$であれば(すなわち、区間がどんどん小さくなっていけば)、共通部分は一点$\alpha$のみからなる集合である。すなわち、

区間縮小法の証明自体はさほど難しくありません。
基本に則り、一歩ずつ前進すれば必ずゴールにたどり着けます。(まあ、それが数学の面白いところだと思います。)
「いざ証明！」とその前に…
区間縮小の原理の証明の流れを説明します。

$\displaystyle \bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$の証明
- (ステップ1-1)　縮小する(範囲がどんどん狭くなる)区間を作り、その区間の端からなる2つの数列を作る。
  このとき、区間の左端からなる数列$\{a_n\}_{n\in\mathbb{N}}$は単調増加数列であり、右端からなる数列$\{b_n\}_{n\in\mathbb{N}}$は単調減少数列である。
- (ステップ1-2) 作った2つの数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{n\in\mathbb{N}}$はそれぞれ上限、下限に収束する。
  これは「有界な単調列は収束する。」という命題を使う！
- (ステップ1-3) 任意の$n\in\mathbb{N}$に対して、$a_n\leq \{a_n\mid n\in\mathbb{N}\}$の上限$\leq \{b_n\mid n\in\mathbb{N}$の下限$\leq b_n$が成り立つ。
  これを証明するために、とある事実(区間縮小法の証明の道中で証明します)を使う！
  任意の自然数$n$に対して、区間$I_n=[a_n,b_n]$の間に属する具体的な要素を見つけることができた。
- (おしまい)
1.で作った2つの数列の差の極限が$0$に収束するとき、作った区間の無限個の共通部分は1点のみからなる集合である、ことの証明
- (ステップ2-1) 区間$I_n$の無限個の共通部分から要素を1つ任意に取ってくる。
  1.により、$\displaystyle \bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$($\displaystyle \bigcap_{n\in\mathbb{N}}I_n$に何か要素が少なくとも1つある)ことから、その要素を1つ取ってくる。
- (ステップ2-2) 取ってきた1つの要素が実は数列$\{a_n\}_{n\in\mathbb{N}}$の極限と一致することを示す。
  今、数列$\{a_n\}_{n\in\mathbb{N}}$と$\{b_n\}_{n\in\mathbb{N}}$の差の極限が一致するため、数列$\{a_n\}{n\in\mathbb{N}}$の極限と数列$\{b_n\}_{n\in\mathbb{N}}$の極限と一致するから(区間縮小法の証明の道中で証明します)、結局は数列$\{a_n\}_{n\in\mathbb{N}}$の極限が区間$I_n$の無限個の共通部分の要素だ、という結論に至る。
- (おしまい)

区間縮小法の証明

(1.の証明)
(ステップ1-1)
任意の$n$番目の有界な閉区間$I_n$を$I_n=[a_n,b_n]$とします。
すると、任意の自然数$n$に対して$a_n$および$b_n$をそれぞれ集めた数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{n\in\mathbb{N}}$ができます。
また、この$I_n$が
$$I_1\supset I_2\supset \dots I_n\supset I_{n+1}\supset\dots$$
を満たすとします。
つまり
$$a_1\leq a_2\leq \dots \leq a_{n-1} \leq a_n\leq\dots \leq b_n\leq b_{n-1}\leq \dots \leq b_2\leq b_1\cdots①$$
を満たすとします。
①により、任意の$n\in\mathbb{N}$に対して、$a_1\leq a_n$であり、$b_n\leq b_1$が成り立つのだから、数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}{n\in\mathbb{N}}$はそれぞれ上に有界であり、下に有界です。
さらに、①から、数列$\{a_n\}_{n\in\mathbb{N}}$単調増加数列であり、$\{b_n\}{n\in\mathbb{N}}$は単調減少数列です。
従って、数列$\{a_n\}_{n\in\mathbb{N}}$は上に有界な単調増加数列であり、数列$\{b_n\}_{n\in\mathbb{N}}$は下に有界な単調減少数列です。

(ステップ1-2)
ここで、「有界な単調列は収束する」という事実、すなわち

有界な単調列は収束する。 上に有界な単調増加列はその上限に収束する。すなわち、数列$\{x_n\}_{n\in\mathbb{N}}$が

$(\exists S\in\mathbb{R})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ x_n\leq S)$,
$(\forall n\in\mathbb{N})\ x_n\leq x_{n+1}$

を満たすならば、 $$(\exists X\in\mathbb{R})\ \displaystyle\lim_{n\to\infty}x_n=X$$ である。さらに、$X=S$である。
また、下に有界な単調減少列はその下限に収束する。すなわち、数列$\{y_n\}_{n\in\mathbb{N}}$が

$(\exists L\in\mathbb{R})\ {\rm s.t.}\ (\forall n\in\mathbb{N}\ y_n\geq L)$,
$(\forall n\in\mathbb{N})\ y_n\geq y_{n+1}$

を満たすならば、 $$(\exists Y\in\mathbb{R})\ \displaystyle\lim_{n\to\infty}y_n=Y$$ である。さらに、$Y=L$である。

を使います。
すると、数列$\{a_n\}_{n\in\mathbb{N}}$はその上限$\alpha$に収束し、数列$\{b_n\}{n\in\mathbb{N}}$はその下限$\beta$に収束します。
すなわち、
$$(\exists \alpha\in\mathbb{R})\ {\rm s.t.}\ \lim_{n\to\infty}a_n=\alphaかつ(\exists \beta\in\mathbb{R})\ {\rm s.t.}\ \lim_{n\to\infty}b_n=\beta$$
であり、$\alpha$は$\{a_n\mid n\in\mathbb{N}\}$の上限、$\beta$は$\{b_n\mid n\in\mathbb{N}\}$の下限です。

(ステップ1-3)
従って、$\alpha$は$\{a_n\mid n\in\mathbb{N}\}$の上界であるから、任意の$n\in\mathbb{N}$に対して$a_n\leq\alpha$であり、$\beta$は$\{b_n\mid n\in\mathbb{N}\}$の下界であるから、任意の$n\in\mathbb{N}$に対して$\beta\leq b_n$です。
さらに、①から任意の$n\in\mathbb{N}$に対して$a_n\leq b_n$であるから、$\alpha\leq\beta$です。
これは次が成り立つためです。

補題3.(極限の大小関係) 常に自分より大きいか等しい値を取る数列の極限は自分の極限よりも大きいか等しい。
すなわち、実数の数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{n\in\mathbb{N}}$がそれぞれ$A$および$B$に収束するとする。すなわち、 $$\lim_{n\to\infty}a_n=Aかつ\lim_{n\to\infty}b_n=B$$ であるとする。このとき、 $$(\forall n\in\mathbb{N})\ a_n\leq b_nならば A\leq B$$ が成り立つ。

補題3.の証明

$\displaystyle\lim_{n\to\infty}a_n=A$かつ$\displaystyle\lim_{n\to\infty}b_n=B$とするとき、$A\leq B$を証明すればOKです。
背理法を用います。
仮に、$A>B$とします。
数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{n\in\mathbb{N}}$はそれぞれ収束するのだから、

$(\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\epsilon_1)$,
$(\forall \epsilon_2>0)(\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-B|<\epsilon_2)$

が成り立ちます。
これは、任意の正の実数$\epsilon_1$および$\epsilon_2$に対して

$\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\epsilon_1$
$\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-B|<\epsilon_2$

が成り立っているということなのだから、
$$\epsilon_1=\epsilon_2=\frac{A-B}{2}$$
としても成り立ちます。
したがって、

$\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\displaystyle\frac{A-B}{2}$
$\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-A|<\displaystyle\frac{A-B}{2}$

が成り立ちます。
ここで、$N$を$N_1$と$N_2$のうち大きい方とします。
記号で書けば、$N=\max\{N_1,N_2\}$とします。
このとき、$n\geq N$を満たす自然数$n$に対して、
$$a_n>A-\frac{A-B}{2}かつ-b_n>-B-\frac{A-B}{2}$$
です。
故に
$$a_n-b_n>A-B-2\cdot\frac{A-B}{2}=A-B-(A-B)=0$$
となります。
すなわち$a_n>b_n$です。
しかし、これは仮定$(\forall n\in\mathbb{N})\ a_n\leq b_n$に矛盾します。
従って、$A\leq B$です。

補題3.の証明終わり

では、(ステップ1-3)に戻りましょう。
今示した補題3.により$\alpha\leq\beta$です。
従って、任意の$n\in\mathbb{N}$に対して、
$$a_n\leq\alpha\leq\beta\leq b_n$$
です。
ということは、$\alpha$および$\beta$は任意の$n\in\mathbb{N}$に対して区間$I_n=[a_n,b_n]$に含まれるということであるから、$\displaystyle\alpha,\beta\in\bigcap_{n\in\mathbb{N}}I_n$です。
これはまさに、
$$\bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$$
です。

(2.の証明)
(ステップ2-1)
今、1.が成り立ったのだから、すなわち、$\displaystyle\bigcap_{n\in\mathbb{N}}I_n\neq\emptyset$が成り立ったのだから、$\displaystyle　c\in\bigcap_{n\in\mathbb{N}}I_n$という要素$c$を取ることができます。
すなわち、任意の$n\in\mathbb{N}$に対して、$c\in I_n=[a_n,b_n]$であるから
$$(\forall n\in\mathbb{N})\ a_n\leq c\leq b_n$$
です。
(ステップ2-2)
また、任意の$n\in\mathbb{N}$に対して、$a_n\leq \alpha$であるから、任意の$n\in\mathbb{N}$に対して
$$a_n-\alpha\leq c-\alpha\leq b_n-\alpha\leq b_n-a_n$$
故に、
$$0\leq|c-\alpha|\leq|b_n-a_n|=b_n-a_n$$
です。
従って、補題3.から
$$\lim_{n\to\infty}0\leq\lim_{n\to\infty}|c-\alpha|\leq\lim_{n\to\infty}(b_n-a_n)$$
です。
ここで、定数列はその定数に収束するので、
$$0\leq|c-\alpha|\leq\lim_{n\to\infty}(b_n-a_n)$$
です。
これが正しいことを示します。

補題4.(定数列の極限) 一定の値を取り続ける数列はその定数に収束する。
すなわち、 $\{a_n\}_{n\in\mathbb{N}}$を実数の数列とする。このとき、ある実数$c$が存在して、任意の$n\in\mathbb{N}$に対して$a_n=c$であるとき、$\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}c=c$である。

補題4.の証明

$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-c|<\epsilon)$$
を示せばOKです。
しかしこれはほぼ明らかなようなものです。
任意の$\epsilon>0$に対して、$N=1$とすると、$n\geq N$、すなわち$n\geq 1$を満たす自然数$n$に対して、
$$|a_n-c|=|c-c|=|0|=0<\epsilon$$
です
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-c|<\epsilon)$$
であるから、$\displaystyle\lim_{n\to\infty}a_n=\lim_{n\to\infty}c=c$です。

補題4.の証明終わり

では、(ステップ2-2)の証明に戻ります。
補題4.から
$$0\leq|c-\alpha|\leq\lim_{n\to\infty}(b_n-a_n)$$
です。
今、$\displaystyle \lim_{n\to\infty}(b_n-a_n)=0$であるから、
$$0\leq|c-\alpha|\leq0$$
です。
従って、$|c-\alpha|=0$でなければなりません。
ゆえに$c=\alpha$です。
以上のことから、
$$\bigcap_{n\in\mathbb{N}}I_n=\{\alpha\}$$
です。
特に、今、$\displaystyle \lim_{n\to\infty}(b_n-a_n)=0$であるから、
$$\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}b_n-\lim_{n\to\infty}a_n=\beta-\alpha=0$$
です。
これは収束する数列の差の極限は各数列の極限の差と等しいという事実から得られます。
次で示します。

補題5.(差の極限) 収束する数列の差の極限は各数列の極限の差と等しい。
すなわち、数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}_{n\in\mathbb{N}}$がそれぞれ$A$および$B$に収束したとする。このとき、$\displaystyle\lim_{n\to\infty}(a_n-b_n)=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n=A-B$である。

補題5.の証明

示したいことは、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |(a_n-b_n)-(A-B)|<\epsilon)$$
です。
今、数列$\{a_n\}_{n\in\mathbb{N}}$および$\{b_n\}{n\in\mathbb{N}}$がそれぞれ$A$および$B$に収束しているのだから、

$(\forall \epsilon_1>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\epsilon_1)$
$(\forall \epsilon_2>0)(\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-B|<\epsilon_2)$

が成り立っています。
すなわち、上記を満たすような自然数$N_1$および$N_2$を見つけることができます。
さらに、上記は任意の正の実数$\epsilon_1$および$\epsilon_2$に対して成り立つので、新たに任意の正の実数$\epsilon$を使って
$$\epsilon_1=\epsilon_2=2\epsilon$$
としても成り立ちます。
故に、

$(\forall \epsilon>0)(\exists N_1\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |a_n-A|<\displaystyle\frac{\epsilon}{2})$
$(\forall \epsilon>0)(\exists N_2\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |b_n-B|<\displaystyle\frac{\epsilon}{2})$

が成り立ちます。
このとき、$N$を$N_1$と$N_2$のうち大きい方とします。
記号でかけば$N=\max\{N_1,N_2\}$とします。
$n\geq N$を満たす任意の自然数$n$に対して、
$$|(a_n-b_n)-(A-B)|=|(a_n-A)+(B-b_n)|\\ \leq |a_n-A|+|B-b_n|=|a_n-A|+|b_n-B|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon$$
である。ただし、任意の実数$x,y$に対して、$|x+y|\leq |x|+|y|$である事実を使いました。
従って、
$$(\forall \epsilon>0)(\exists N\in\mathbb{N}\ {\rm s.t.}\ \forall n\in\mathbb{N}\ n\geq N\Rightarrow |(a_n-b_n)-(A-B)|<\epsilon)$$
であるから、
$\displaystyle\lim_{n\to\infty}(a_n-b_n)=\lim_{n\to\infty}a_n-\lim_{n\to\infty}b_n=A-B$です。

補題5.の証明終わり

では、(ステップ2-2)の証明に戻ろう。
補題5.により、
$$\lim_{n\to\infty}(b_n-a_n)=\lim_{n\to\infty}b_n-\lim_{n\to\infty}a_n=\beta-\alpha=0$$
です。
従って、
$$\lim_{n\to\infty}a_n=\lim_{n\to\infty}b_n=\alpha$$
です。

区間縮小法の証明終わり

結

今回は区間縮小の原理を「有界な単調列は収束する。」という命題から証明しました。

次回は「区間縮小法と実数の連続性の関係は？」です。
すなわち、区間縮小法+アルキメデスの原理(証明も与える)からデデキントの定理を示します。

乞うご期待！質問、コメントなどお待ちしております！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34