「ダルブーの定理を証明しよう！」【解析学の基礎シリーズ】積分編 その3

本記事の内容

本記事はダルブーの定理を証明する記事です。

本記事を読むにあたり、積分について知っている必要があるため、以下の記事も合わせて御覧ください。

「積分って？イメージは？」【解析学の基礎シリーズ】積分編 その1

...

for-spring.com

2022.08.10

ダルブーの定理の説明の前に…

ダルブーの定理の説明の前に、今回から数回(おそらく3回)の目標を述べておきます。

今回から数回掛けての目標は

です。

リーマン積分はどのように定められていか、というと、リーマン和の極限でもって定められています。
リーマン和$s\left(f;\Delta;\boldsymbol{\xi} \right)$は分割$\Delta$のみではなくて、小区間$I_k$の代表点$\xi_k$の取り方にも依存します。
そして、どのように$\xi_k$を取ったとしても、$d(\Delta)\to0$のとき、ある実数に収束するときに、$f$は可積分だというのでした。

今回は、分割$\Delta$に着目します。

下積分、上積分

下積分、上積分のイメージは大したことありません。

前々回の記事(【解析学の基礎シリーズ】積分編 その1)で説明した積分のイメージを思い出してみて下さい。

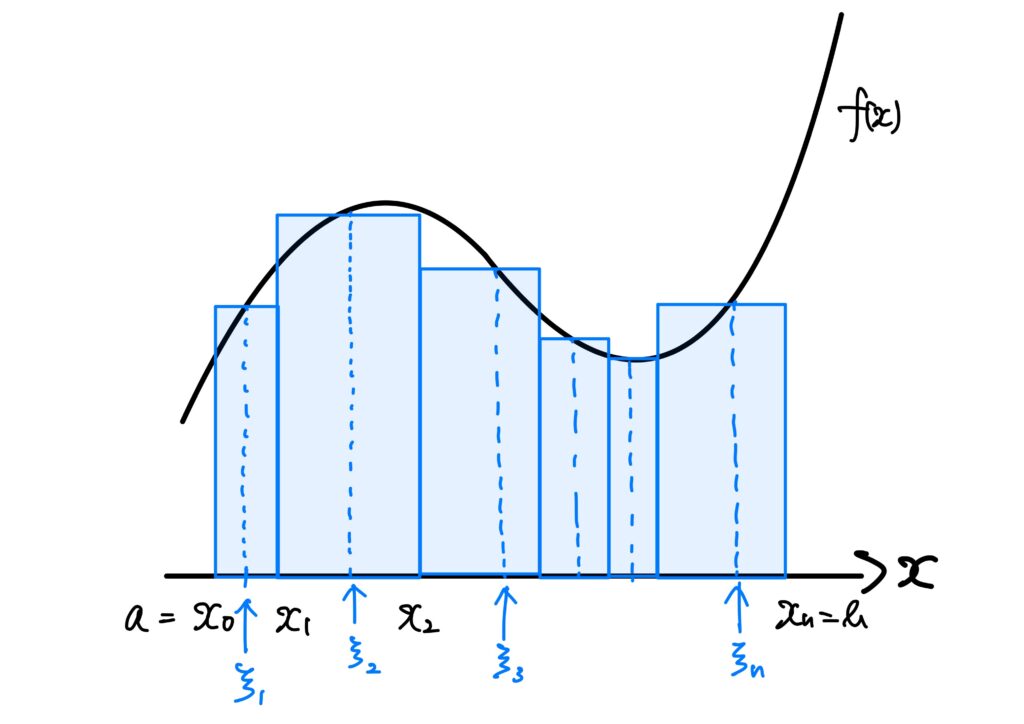
これは1変数の場合ですが、この図において青い長方形の面積の和がリーマン和です。
これを見ると、青い長方形は$y=f(x)$の上にはみ出していたり、$y=f(x)$の下に来ていたりします。

イメージでいうと、この上にはみ出ている部分のリーマン和の極限が上積分で、下に来ている部分のリーマン和の極限が下積分です。

上積分、下積分を厳密に語るために、少々準備をします。

振幅

$\mathbb{R}^n$の有界閉区間を$I$とします。
有界な実数値関数$f:I\to\mathbb{R}$に対して、
$$m=\inf_{\boldsymbol{x}\in I}f(\boldsymbol{x}),\quad M=\sup_{\boldsymbol{x}\in I}f(\boldsymbol{x})$$
とすると、
$$m\leq f(\boldsymbol{x})\leq M\quad (\forall\boldsymbol{x}\in I)$$
です。
このとき、任意の$\boldsymbol{x},\boldsymbol{y}\in I$に対して、
$$m\leq f(\boldsymbol{x})\leq M,\quad m\leq f(\boldsymbol{y})\leq M$$
なわけですので、
$$-M+m\leq f(\boldsymbol{x})-f(\boldsymbol{y})\leq M-m$$
だから、
$$\left|f(\boldsymbol{x})-f(\boldsymbol{y})\right|\leq M-m$$
です。
ここで、$f$は実数値関数ですので、$f(\boldsymbol{x})$は実数です。
同様に$f(\boldsymbol{y})$もまた実数です。
従って、実数の連続性から、実数$\left|f(\boldsymbol{x})-f(\boldsymbol{y})\right|$のいくらでも近くにまた実数が存在するので、
$$\sup_{\boldsymbol{x},\boldsymbol{y}\in I}\left|f(\boldsymbol{x})-f(\boldsymbol{y})\right|=M-m$$
です。
この$M-m$、すなわち$\displaystyle\sup_{\boldsymbol{x},\boldsymbol{y}\in I}\left|f(\boldsymbol{x})-f(\boldsymbol{y})\right|$を$f$の$I$における振幅といい、$a(f,I)$で書きます。

$M-m$は$f$の上にはみ出た部分と下に来ている部分の差なので、まさに振幅といったところです。

不足和、過剰和

$\mathbb{R}^n$の区間$I$の任意の分割$\Delta$に対して、$\Delta$により得られる各小区間$I_k\ (k\in K(\Delta))$において
$$m_k=\inf_{\boldsymbol{x}\in I_k}f(\boldsymbol{x}),\quad M_k=\sup_{\boldsymbol{x}\in I_k}f(\boldsymbol{x})$$
とおけば、振幅の話のときと同様にして
$$m_k\leq f(\boldsymbol{x})\leq M_k\quad (\boldsymbol{x}\in I_k)\cdots①$$
です。

今、このとき和
$$s_{\Delta}=\sum_{k\in K(\Delta)}m_kv(I_k),\quad S_\Delta=\sum_{k\in K(\Delta)}M_kv(I_k)$$
をそれぞれ分割$\Delta$に関する$f$の不足和、過剰和といいます。

これらはまさに、先程の図における$f(\boldsymbol{x})$の下にある長方形の面積の和、$f(\boldsymbol{x})$からはみ出ている長方形の面積の和を表しています(密度$\times$体積の和というリーマン和の形をしていますね！)。

これらは$f$の積分が存在するときにそれぞれ下から、上から近似するものです。
この不足和、過剰和を「ある関数$f$に対して」と明記したいときには$s_\Delta(f)$、$S_\Delta(f)$と書きます。

さて、①からすぐわかるのですが、どのように代表点$\xi_k$を取ったとしても、
$$s_{\Delta}\leq s\left(f;\Delta;\boldsymbol{\xi} \right)\leq D_\Delta$$
です。
実際、①は任意の$\boldsymbol{x}\in I$で成り立つからです。

上積分、下積分

さて、この章の本題なわけですが、分割$\Delta$を更に細かく分けていくときに、$s_\Delta$はだんだん増え、逆に$S_\Delta$はだんだん減っていきます。
「本当に？」と思うかもしれませんが、後で証明します。

一旦ここでは分割$\Delta$を更に細かく分けていくときに、$s_\Delta$はだんだん増え、逆に$S_\Delta$はだんだん減っていくことを認めたとしましょう。
すると、$\mathbb{R}^n$の区間$I$のありとあらゆる分割$\Delta$に対する$s_\Delta$の上限、$S_\Delta$の下限
$$s=\sup_{\Delta\in\mathcal{D}}s_\Delta,\quad S=\inf_{\Delta\in\mathcal{D}}S_\Delta$$
を考えることができます。
ただし、$\mathcal{D}$は$I$の分割全体の集合です。

さて、先程の$s$と$S$をそれぞれ$f$の下積分、上積分と言います。

不足和、過剰和は分割を細かくするとそれぞれ増加、減少します。

さて、先程認めた、分割を細かくすると、不足和と過剰和がそれぞれ増加、減少するということを証明します。

と、との前に話をわかりやすくするために記号を導入します。

細分

ここで注意なのが、記号$\Delta\leq \Delta^\prime$は大小関係の記号$\leq$を用いていますが、大小関係を表す記号ではありません。
そもそも分割は集合なので、集合そのものに大小関係はありません(にたようなものとして部分集合がありますが)。

単に２つの分割$\Delta$と$\Delta^\prime$が与えられたとき、$\Delta$の各辺の分点がすべて$\Delta^\prime$の分点となっているという”関係”を$\Delta\leq\Delta^\prime$と書く、という話です。

不足和、過剰和は分割を細かくするとそれぞれ増加、減少します。

では、主張を明示します。

命題1.の証明

分割$\Delta^\prime$が分割$\Delta$に唯一つの分点をある辺で追加して得られる場合にのみ証明すればOKです。
実際、何個の分点を追加したとしても、１つの分点を追加する、という操作を繰り返すことで得られるからです。

さて、$\Delta^\prime$において、ある小区間$I_k\ (k\in K(\Delta))$が$I_k^\prime$と$I_k^{\prime\prime}$に分割されたとしましょう。

そこにおける$f(\boldsymbol{x})$の上限(下限)を$M_k^\prime$、$M_k^{\prime\prime}$($m_k^\prime$、$m_k^{\prime\prime}$)としましょう。

このとき、
$$\begin{eqnarray} &&m_k\leq m_k^\prime,\ m_k^{\prime\prime},\\ &&M_k^\prime,\ M_k^{\prime\prime}\leq M_k \end{eqnarray}$$
かつ
$$v(I_k)=v(I_k^\prime)+v(I_k^{\prime\prime})$$
です。
従って、
$$\begin{eqnarray} m_kv(I_k)&=&m_kv(I_k^\prime)+m_kv(I_k^{\prime\prime})\\ &\leq&m_k^\prime v(I_k^\prime)+m_k^{\prime\prime}v(I_k^{\prime\prime}) \end{eqnarray}$$
となるから、$s_\Delta\leq s_\Delta^\prime$です。
同様にして、$S_\Delta^\prime\leq S_\Delta$です。

命題1.の証明終わり

ダルブーの定理

ダルブーの定理がどういう定理かを説明する前に、なんのためにダルブーの定理を証明するか、ということについて述べておきます。

それはもちろん「可積分であることの必要十分条件を導くため」なわけですが、少しだけ先取りをすると$s=S$のときが可積分であることの必要十分条件です。
これを示すには、上限、下限として定められた$s$、$S$が$d(\Delta)\to0$のときの$s_\Delta$と$S_\Delta$の極限であることを示す必要があります。
これを表現しているのがダルブーの定理です。

ちなみに、$s=\sup s_\Delta$は、すべての分割$\Delta$に対して$s_\Delta\leq s$で、任意の$\varepsilon>0$に対して$s-\varepsilon<s_\Delta$となる$\Delta\in\mathcal{D}$が少なくとも１つは存在しますよ、という意味になります。

一方で、$s_\Delta\to s\ ( d(\Delta)\to0)$は、任意の$\varepsilon>0$に対してある$\delta>0$が存在して、$d(\Delta)<\delta$となるすべての分割$\Delta$に対して、$S-\varepsilon<s_\Delta\leq s$が成り立つことです。

これは$s$または$S$を$f$の積分に結びつける事実です。

定理2.の証明

どちらの場合も同様ですので、今回は下積分$s$について証明をします。

そもそも、$s$は$s=\sup s_\Delta$、すなわち上限として定められていたので、
$$(\forall \varepsilon>0)\ (\exists D\in\mathcal{D})\ {\rm s.t.}\ 0\leq s-s_D\leq \frac{\varepsilon}{2}\cdots①$$
が成り立っています。
この$D$を一つ固定しましょう。

さて、$I$の任意の分割$\Delta$と$D$の分点をあわせたものを分点とする分割を$\Delta^\prime$とします。
このとき、$\Delta^\prime$は$\Delta$と$D$の共通部分の細分です。
すなわち、$\Delta\leq\Delta^\prime$、$D\leq \Delta^\prime$です。

このとき、命題1.により
$$0\leq s_{\Delta^\prime}-s_\Delta,\quad0\leq s_{\Delta^\prime}-s_D\cdots②$$
が成り立ちます。

今、$d(\Delta)\to0$という極限を考えるので、$d(\Delta)$が十分小さいような$\Delta$だけを考えればOKです。
そこで、$D$により得られる小区間の辺の長さのうち、最も短いもの、すなわち辺の長さの最小値を$e$として、不等式
$$d(\Delta)<e\cdots③$$
を満たす$\Delta$を考えます。
このとき、$\Delta$によって得られる小区間$I_k\ k(\in K(\Delta))$の各辺の長さは$d(\Delta)$以下なので、

ということになります。
さて、任意の$k\in K(\Delta)$に対して、$n$次元区間$I_k$の$n$個の辺の内部に含まれる$D$の分点の総数を$n_k$としましょう。
④から、$0\leq n_k\leq n$です。
分割$\Delta^\prime$では$I_k$は$p_k$個の小区間$I_k^l\ (1\leq l\leq p_k)$に分かれるとしましょう。
$m_k^l=\inf\{f(\boldsymbol{x})|\boldsymbol{x}\in I_k^l\}$とすると、
$$m\leq m_k\leq m_k^l\leq M,\quad \sum_{l=1}^{p_k}v(I_k^l)=v(I_k)$$
ですので、差$s_{\Delta^\prime}-s_\Delta$の$I_k$に関する部分
$$d_k=\sum_{l=1}^{p_k}(m_k^l-m_k)v(I_k^l)$$
は、$n_k=0$のときに$d_k=0$で、$n_k>0$のときに$d_k\leq (M-m)v(I_k)$を満たします。
そこで、$D$の分点によって実際に分割される$I_k$(つまり、$n_k>0$であるような$I_k$)の体積の和を
$$V_\Delta=\sum_{n_k>0}v(I_k)$$
とおくと、
$$0\leq s_{\Delta^\prime}-s_\Delta\leq (M-m)V_\Delta\cdots⑤$$
が成り立ちます。
このとき、$D$と$I$のみで定まって、$\Delta$に依存しない定数$c\geq0$が存在して、
$$0\leq V_\Delta\leq c\cdot d(\Delta)\cdots (*)$$
が成り立ちます。
この(＊)の証明は一旦後回しにして、(＊)を認めることでダルブーの定理が成り立つことを先に示します。

今、任意の$\varepsilon>0$に対して、
$$0<\delta<\min\left\{e,\frac{\varepsilon}{2(c+1)(M-m+1)}\right\}$$
を満たす$\delta>0$を取ります。
このとき、$d(\Delta)<\delta$を満たすような任意の分割$\Delta$は③、⑤、(＊)を満たすので、不等式
$$0\leq s_{\Delta^\prime}-s_\Delta<\frac{\varepsilon}{2}\cdots⑥$$
が成り立ちます。
そこで、①、②、⑥により、$d(\Delta)<\delta$となる任意の分割$\Delta$に対して、
$$\begin{eqnarray} 0\leq s-s_\Delta&=&(s-s_D)-(s_{\Delta^\prime}-s_D)+(s_{\Delta^\prime}-s_\Delta)\\ &\leq&(s-s_D)+(s_{\Delta^\prime}-s_\Delta)<\frac{\varepsilon}{2}+\frac{\varepsilon}{2}=\varepsilon \end{eqnarray}$$  
です。
これはまさに、$\displaystyle\lim_{d(\Delta)\to0}s_\Delta=s$を意味しています。

(＊)の証明

では、論破するために、(＊)を証明します。

今、$I$の辺$[a_i,b_i]$の内部$(a_i,b_i)$にある$D$の分点の数を$r_i$個としましょう。
$\Delta$により得られる小区間$I_k\ (k\in K(\Delta))$のうち、実際に$D$の分点で分割されるものの和集合の体積$V_\Delta$は、$\Delta$によらない定数$c\geq0$により、$V_\Delta\leq c\cdot d(\Delta)$となることを示すのが目標です。

今、$I$の第$i$辺$[a_i,b_i]$の内部にある$D$の1つの分点に注目します。
この$D$の分点を辺の内部に含む$I_k\ (k\in K(\Delta))$の全部の和集合は、1つの$n$次元区間で、その第$i$辺の長さは$d(\Delta)$以下であり、$j\neq i$のときは、第$j$辺の長さは$b_j-a_j$です(下図の青い部分)。

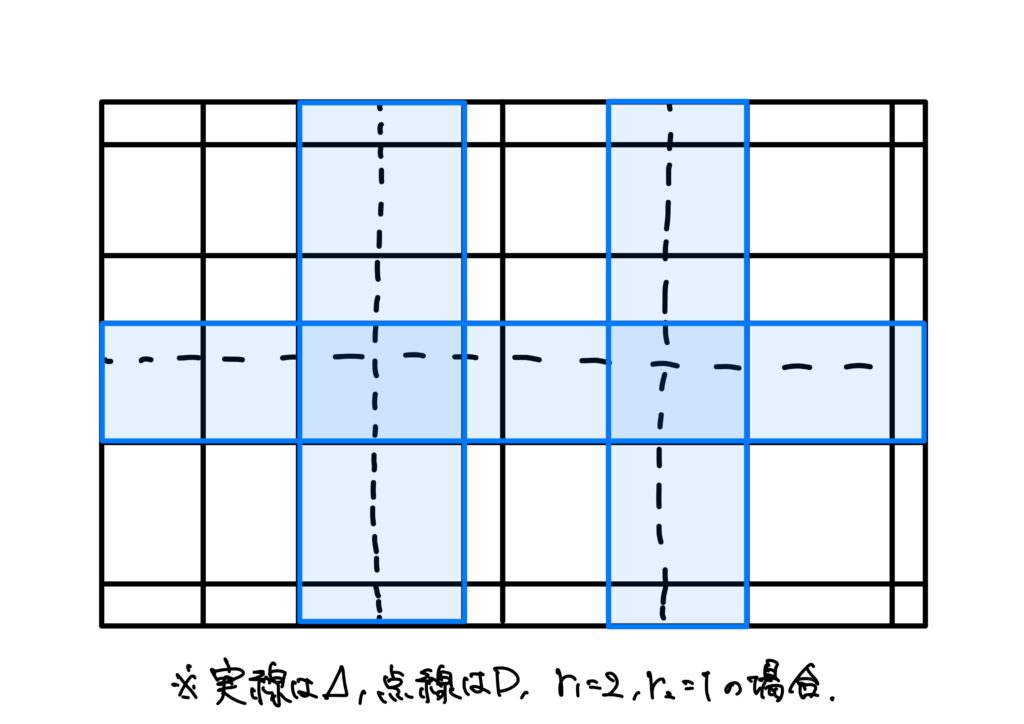
従って、その体積は
$$d(\Delta)\prod_{j\neq i}(b_j-a_j)=c\cdot d(\Delta)$$
以下になります。
このような$n$次元区間が第$i$辺について$r_i$個以下あるということです。

そこで、それらの和を考えることで、$D$の分点で、実際に分割される$\Delta$の小区間の体積の和$V_\Delta$は
$$0\leq V_{\Delta}\leq \sum_{i=1}^n r_ic_id(\Delta)=cd(\Delta)$$
を満たします。
ここで、
$$c=\sum_{i=1}^n r_ic_i=\sum_{i=1}^n r_i\prod_{j\neq i}(b_j-a_j)$$
は$D$と$I$のみで定まる定数で、かつ$0$以上です。

定理2.の証明終わり

さて、このダルブーの定理を使うことで有界な関数$f$が有界閉区間$I$で可積分であるための必要十分条件が得られます。

これについては次回行います。

読者の皆様のコメントをください！

筆者が初めて積分を大学で学んだとき「難しいなあ」と思ったのですが、同時に「高校数学でやっていた積分は計算だったんだ。」と痛感しました。
確かに、計算ができる、というのは重要なことなのですが、なぜその計算をすることができるのかということの方がむしろ重要だと思います。

しかし、その「計算する」という操作ができるまでには歴史的にも時間がかかっているようです。

そんな中、大学のとある教授が数学の歴史を織り交ぜて講義をしてくださいました。
これは有名な話なのですが、微分積分学の祖はかのアイザック・ニュートンとゴットフリート・ライプニッツ(“祖”と言い切ってしまうと実はちょっと違うんですが…彼らの前にも似たようなことを考えていた人がいるようなので。)

さて、それをきっかけに筆者は数学史にちょっと興味を持って調べてみました。
ユークリッドの話だったりとか、色々です。
ユークリッドの話でいくと、こんな逸話があるようです。

ユークリッドがアカデメイアで幾何学の講義をしているときに、ある学生が挙手してユークリッドに質問しました。

学生「先生、これを学んで何の役に立つんですか？」

すると、ユークリッドは奴隷を呼んで、奴隷に金貨を渡し、

ユークリッド「彼にこの金貨をあげなさい。彼は学んだことから直ちに見返りがなければならないようだ。」

といったそうです。
筆者は結構好きな話なんですよね。

そこで「この学者(数学者に限らず)のこの逸話がおもしろい！」というのがあればぜひコメントで教えて下さい！

結

今回はダルブーの定理について解説しました。
ダルブーの定理は上積分と下積分というもので可積分条件を語っている定理です。
これは有界閉集合を定義域とする有界な関数が可積分であることの必要十分条件を導き出すのに重要な定理です。

次回は可積分条件①として、有界な関数がどういうときに可積分なのかということを解説します。

乞うご期待！
質問、コメントなどお待ちしております！
どんな些細なことでも構いませんし、「定理〇〇の△△が分からない！」などいただければ全てお答えします！
お問い合わせの内容にもよりますが、ご質問はおおよそ３日以内にお答えします。
もし直ちに回答が欲しければその旨もコメントでお知らせください。直ちに対応いたします。

Twitterでもリプ、DM問わず質問、コメントを大募集しております！