「関数の連続って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その５

本記事の内容

本記事は「関数の連続って数学的にどういうこと？」を明示し、実際に証明してみる記事である。

本記事を読むにあたり、関数の連続のイメージがついているとより理解が進むと思われるので、その際は以下の記事を参照してください。

「"関数が連続である"ことのイメージをつかもう！」【解析学の基礎シリーズ】関数の極限編 その4

...

for-spring.com

2022.04.04

また、関数の極限について知っているとより理解が進むと思われるので、その際は以下の記事を参照してください。

「関数の収束って数学的に何？」「実際に証明してみよう！」【解析学の基礎シリーズ】関数の極限編 その２

本記事の内容本記事は関数の収束は数学的にどういうことかを説明し、実際に関数の収束を証明してみる記事である。本記事を読むにあたり数列の収束を理解し、関数の収束のイメージがついているとより理解しやすいと思われるので、その際は以下の記事を参照して

for-spring.com

で？関数の連続って数学的にどういうこと？

前回の記事(【解析学の基礎シリーズ】関数の極限編 その4)で述べたイメージをまとめると、

であった。
これを数学的に表現すると、次になる。

実は、関数の連続には別の言い方もある。
それについては後述する。

関数が連続であることと連続でないことを証明してみよう！

先に挙げた例1.,2.,3.,4.が連続であるかどうかを証明してみよう！
とはいえ、関数の極限、特に関数の収束がわかっていればなんてことはない。
むしろほとんど同じである。
なぜならば、形式的には関数の収束における\(A\)が\(f(a)\)に変わっただけだからである。
「ちょっとやってみようかな。」という方は是非挑戦してみてほしい！

例1.について

例1.
\(f:\mathbb{R}\to\mathbb{R}\)が\(f(x)=2x\)とする。
このとき、\(f\)は\(\mathbb{R}\)で連続であり、特に\(x=0\)で連続である。

証明

1. \(f\)が\(x=0\)で連続であることの証明
   示したいことは
   $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-0|<\delta\Rightarrow |2x-0|<\epsilon)$$
   である。 つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
   \(\displaystyle\delta=\frac{\epsilon}{2}\)とすると、\(\delta>0\)である。
   \(0<|x-0|=|x|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
   $$|2x-0|=|2x|=2|x|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
   が成り立つ。
   従って、
   $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0|x|<\delta\Rightarrow |2x|<\epsilon)$$
   が成り立ったので、\(f\)は\(x=0\)で連続である。
2. \(f\)が\(\mathbb{R}\)で連続であることの証明
   示したいことは
   $$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
   である。
   つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
   \(\delta=\frac{\epsilon}{2}\)とすると、\(\delta>0\)である。
   \(0<|x-a|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
   $$|2x-2a|=2|x-a|<2\delta=2\cdot\frac{\epsilon}{2}=\epsilon$$
   が成り立つ。
   従って、
   $$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
   が成り立ったので、\(f\)は\(\mathbb{R}\)で連続である。(Q.E.D.)

例2.について(例1.の証明をマネしてやってみよう！)

例2.
\(g:\mathbb{R}\to\mathbb{R}\)が\(g(x)=x^2\)で定められているとする。
このとき、\(g\)は\(\mathbb{R}\)で連続であり、特に\(x=0\)で連続である。

証明

1. \(g\)が\(x=0\)で連続であることの証明
   示したいことは
   $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-0|<\delta\Rightarrow |x^2-0|<\epsilon)$$
   である。
   つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
   \(\delta=\sqrt{\epsilon}\)とすると、\(\delta>0\)である。
   \(0<|x-0|=|x|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
   $$|x^2-0|=|x^2|=x^2<\delta^2<\epsilon$$が成り立つ。
   従って、
   $$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x|<\delta\Rightarrow |x^2|<\epsilon)$$
   が成り立ったので、\(f\)は\(x=0\)で連続である。
2. \(f\)が\(\mathbb{R}\)で連続であることの証明
   示したいことは
   $$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |2x-2a|<\epsilon)$$
   である。
   つまり、任意の\(\epsilon>0\)に対して上記を満たすような\(\delta>0\)を見つけてきなさい、ということである。
   \(\delta=-|a|+\sqrt{|a|^2+\epsilon}\)とすると、\(\delta>0\)である。
   \(0<|x-a|<\delta\)を満たす\(x\in\mathbb{R}\)に対して、
   \begin{eqnarray}
   |x^2-a^2|&=&|(x+a)(x-a)|\\
   &=&|x-a+2a|\cdot|x-a|\leq |x-a|^2+2|a|\cdot|x-a|\\
   &=&|a|^2-2|a|\sqrt{|a|^2+\epsilon}+|a^2|+\epsilon+2|a|(-|a|+\sqrt{|a|^2+\epsilon})\\
   &=&2|a|^2-2|a|^2+2|a|\sqrt{|a|^2+\epsilon}-2|a|\sqrt{|a|^2+\epsilon}+\epsilon=\epsilon \end{eqnarray}
   が成り立つ。
   従って、
   $$(\forall a\in\mathbb{R})(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |x^2-a^2|<\epsilon)$$
   が成り立ったので、\(f\)は\(\mathbb{R}\)で連続である。
   (Q.E.D.)

例3.について

例3.
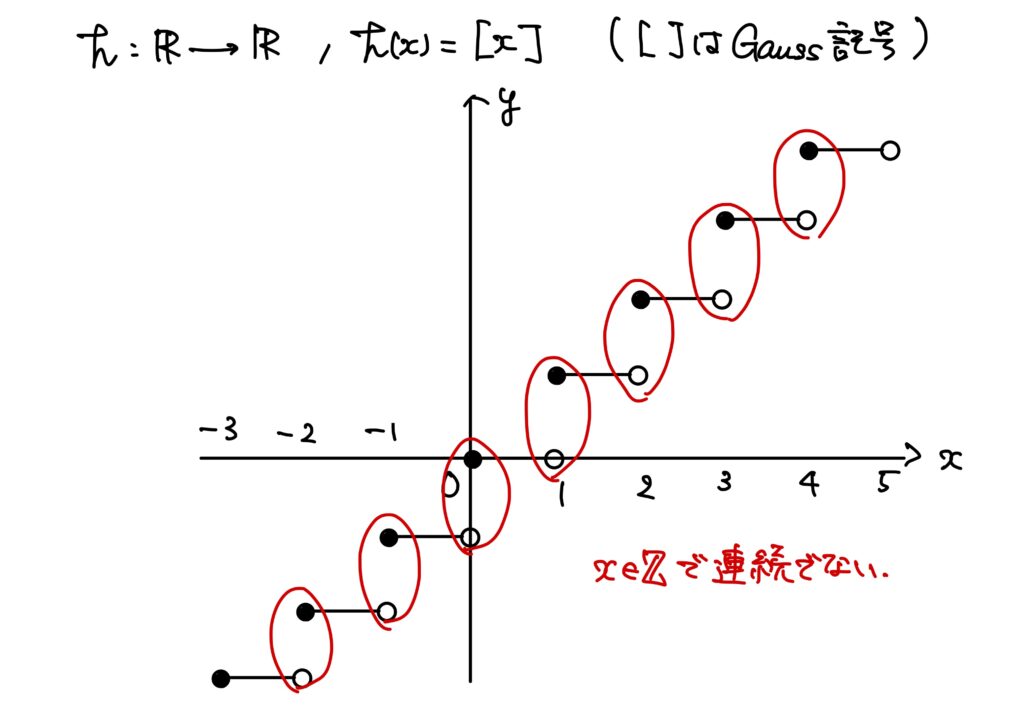
\(h:\mathbb{R}\to\mathbb{R}\)が\(h(x)=[x]\)([]はGauss記号)とする。
このとき\(h\)は\(x\in\mathbb{Z}\)で連続でない。
ここで、\([x]\)は\(x\)を超えない最大の整数である。

(証明)
示したいことは、
$$(\forall n\in\mathbb{Z})(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-n|<\delta \land |h(x)-h(n)|\geq \epsilon]$$
である(\(h\)が\(x=n\in\mathbb{Z}\)で連続であることの否定！)。

つまり、上記を満たすような\(\epsilon>0\)と\(x\in\mathbb{R}\)を見つけてきなさい、ということである。
\(n\in\mathbb{Z}\)とし、\(\epsilon=1\)とする。
また、\(\delta\)を任意の正の実数とする。
このとき、\(x=n-\dfrac{\delta}{2}\)とすると、\(0<|x-n|=\left|-\dfrac{\delta}{2}\right|=\dfrac{\delta}{2}<\delta\)である。 さらに、Gauss記号[]の性質\(x-1<[x]\leq x\)を用いれば、
\begin{eqnarray}
|h(x)-h(n)|&=&\left|\left[ n-\frac{\delta}{2}\right]-n\right|\\
&>&\left|n-\frac{\delta}{2}-1-n\right|\\
&=&\left|-\frac{\delta}{2}-1\right|\\
&=&\frac{\delta}{2}+1>1
\end{eqnarray}
であるので、
$$(\forall n\in\mathbb{Z})(\exists \epsilon>0)\ {\rm s.t.}\ (\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-n|<\delta \land |h(x)-h(n)|\geq \epsilon$$
が成り立つ。
従って、\(h\)は\(x=n\ (n\in\mathbb{Z})\)で不連続である。
(Q.E.D.)

例4.について

例4.
\(u:\mathbb{R}\to\mathbb{R}\)が
$$u(x)=\begin{cases}
x+2&(x\in\mathbb{R}\setminus \{1\})\\
1&(x=1)
\end{cases}$$
で定められていたとする。
このとき、\(\displaystyle \lim_{x\to 1}u(x)=3\)だが、\(u(1)=1\)である。
すなわち、\(u\)は\(x=1\)で不連続である。

(証明)
示したいことは
$$(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-1|<\delta \land |u(x)-u(1)|\geq \epsilon]$$
である(\(u\)が\(x=1\)で連続であることの否定！)。 つまり、上記を満たすような\(\epsilon>0\)と\(x\in\mathbb{R}\)を見つけてきなさい、ということである。
\(\epsilon=1\)とし、\(\delta\)を任意の正の実数とする。
このとき、\(x=\dfrac{\delta}{2}+1\)とすると、\(0<|x-1|=\left|\dfrac{\delta}{2}+1-1\right|=\dfrac{\delta}{2}<\delta\)である。
また、\(\dfrac{\delta}{2}+1>1\)だから\(\dfrac{\delta}{2}+1\neq1\)である。
従って、
$$|u(x)-u(1)|=\left|u\left(\frac{\delta}{2}+1\right)-u(1)\right|=\frac{\delta}{2}+3-1=\frac{\delta}{2}+2>1=\epsilon$$
であるので、
$$(\exists \epsilon>0)\ {\rm s.t.}\ [(\forall \delta>0)(\exists x\in\mathbb{R})\ {\rm s.t.} 0<|x-1|<\delta \land |u(x)-u(1)|\geq \epsilon]$$
が成り立つ。
従って、\(u\)は\(x=1\)で不連続である。
(Q.E.D.)

結

今回は、関数の連続はどういうことかを数学的に明示し、実際に証明を与えた。

関数の連続は「つながっている」ということで、これは数学では極限で表現される。
一言で言ってしまえば、関数が収束して、その収束先が関数の値と一致しているときに連続だ、ということなのである。

次回は「関数の連続の言い換え」ということで、関数の連続を別の言い方をしてみる。
しかし全然難しくはない。
むしろ、次回説明する関数の連続のほうがイメージが湧きやすいかもしれない。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！