「”関数が連続である”ことのイメージをつかもう！」【解析学の基礎シリーズ】関数の極限編その4

本記事の内容
関数の連続のイメージ
1. “つながっている”ってどういうこと？
結

本記事の内容

本記事はイメージ連続な関数のイメージを説明する記事である。

本記事を読むにあたり、関数の極限、特に関数の収束について知っているとよりイメージが湧きやすいと思われるので、その際は以下の記事を参照してください。

関数の連続のイメージ

関数の連続のイメージは、一言でいうと

関数が、区間で”つながっている”。もしくは区間内の点でつながっている。

ということである。

関数が連続であると、嬉しいことがたくさんある。
例えば、閉区間 $[a,b]$ において関数 $f$ が連続であれば、 $[a,b]$ において $f$ は最大値および最小値を持つ。
つまり、閉区間内で連続であれば、最大値と最小値の存在が保証される、というわけである。

では、どんな関数が連続なのか、ということの例を挙げる。

例1.
$f:\mathbb{R}\to\mathbb{R}$ が $f(x)=2x$ とする。
このとき、 $f$ は $\mathbb{R}$ でつながっており、特に $x=0$ でつながっている。

例2.
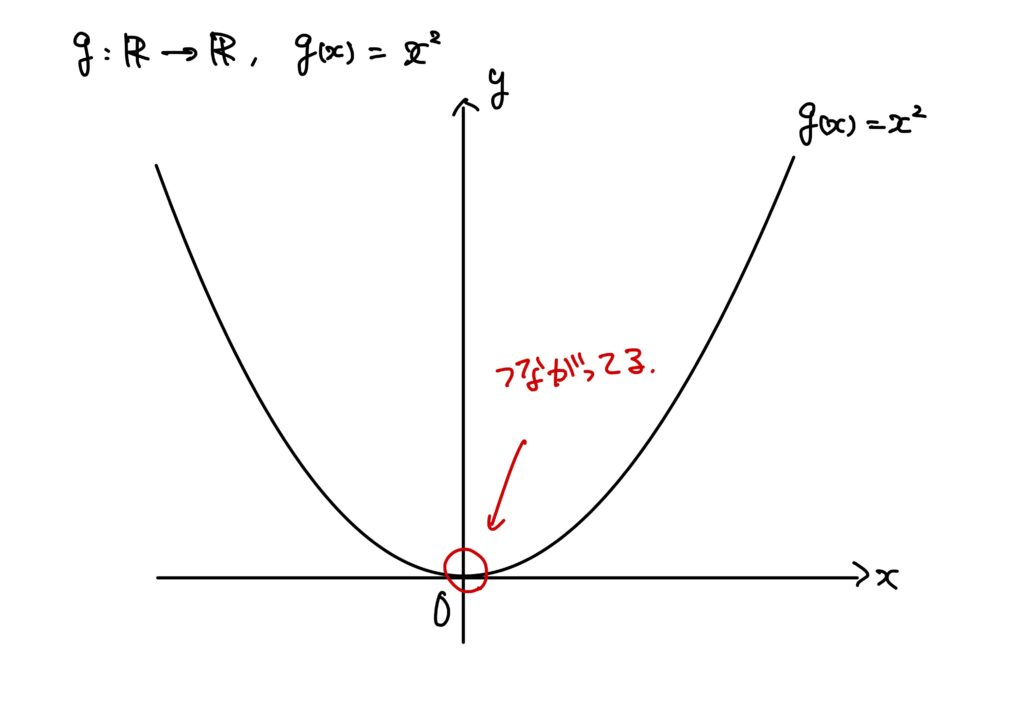
$g:\mathbb{R}\to\mathbb{R}$ が $g(x)=x^2$ で定められているとする。
このとき、 $g$ は $\mathbb{R}$ でつながっており、特に $x=0$ でつながっている。

例3.
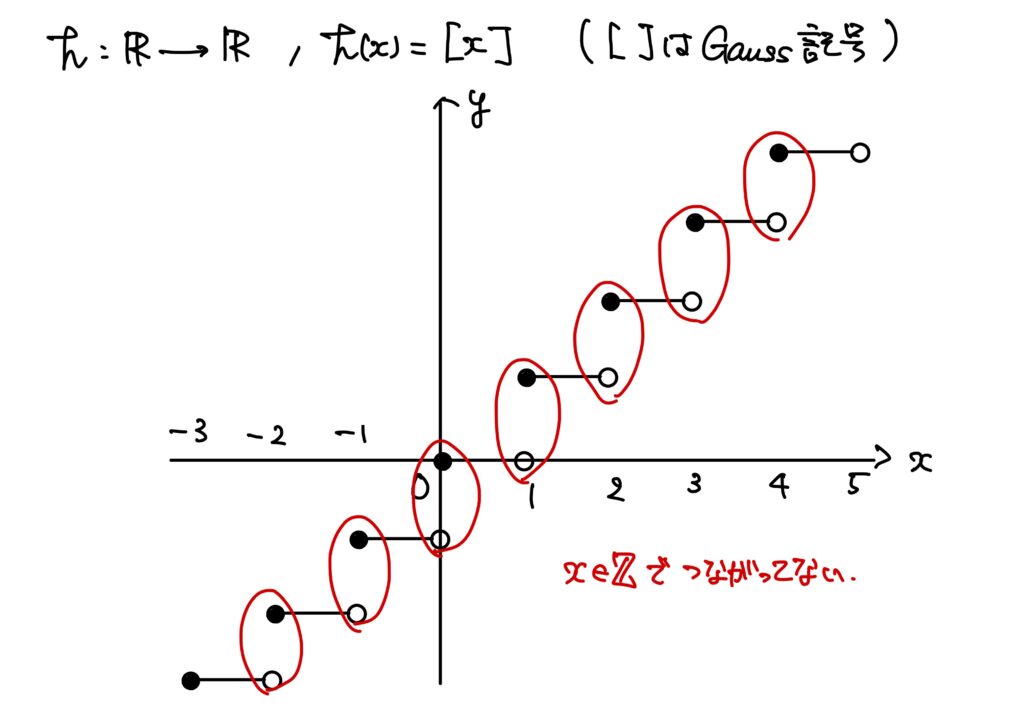
$h:\mathbb{R}\to\mathbb{R}$ が $h(x)=[x]$ ([]はGauss記号)とする。
このとき $h$ は $x\in\mathbb{Z}$ でつながっていない。
ここで、 $[x]$ は $x$ を超えない最大の整数である。

要は

$x=a$ でつながっているときに、

$f$ は

$x=a$ で連続だ。

というわけである。

“つながっている”ってどういうこと？

「”つながっている”というのは直感的に分かるけど、それを数学的に表すとどういうこと？」となるだろう。
これは極限を用いて表す事ができるのである。

ここで、発想を実数の連続性へと戻してみよう。
実数の連続性には2つの直感がある、という話をした(「実数の連続性のイメージをつかもう！」【解析学の基礎シリーズ】)。
それは

実数の数直線上には一切”すき間”が無い。
どんな実数にもその十分近くにまた実数がある。

だった。
まず1.を思い浮かべてみよう。
関数の連続に話を戻すと、”つながっている”ということは”途切れていない”ということなのだから、”一切すき間が無い”ということなのである。
実数の連続性では数直線にすき間が無い、という発想だったのだが、関数の連続は”関数のグラフにすき間が無い”ということなのである。
つまり、イメージとしては数直線をグネグネに曲げたりした線(関数のグラフ)にすき間がない、ということである。

次に2.を思い浮かべてみよう。
実数の連続性については「数直線上のどんな実数に対しても、その十分近くにまた実数がある」ということだった。
この数直線をグネグネ曲げて関数の形にしたと想像してほしい。
このとき、「関数のグラフ上のどんな値に対しても、その十分近くにまた関数の値がある」ということが関数の連続なのである。
これをより数学の言葉に近い形で言えば、

$x$ が

$a$ に近づくとき、

$f(x)$ も

$f(a)$ に近づくというときに

$f$ は

$x=a$ で連続だという。

わけなのである。
故に関数の連続は極限の言葉を用いて書かれるのである。

実関数の収束は何だったか、というと、

実関数の収束

$I$ を

$\mathbb{R}$ の区間、

$f:I\to\mathbb{R}$ を写像(関数)、

$a\in\bar{I}$ 、

$A\in\mathbb{R}$ とする。

$x\to a$ のとき

$f(x)$ が $A$ に収束する(このことを

$f(x)\to A\ (x\to a)$ と表す)とは、

$(\forall \epsilon>0)(\exists \delta>0)\ {\rm s.t.}\ (\forall x\in I:\ 0<|x-a|<\delta\Rightarrow |f(x)-A|<\epsilon)$ が成り立つことをいう。

$A$ のことを

$x\to a$ のときの

$f(x)$ の極限と呼び、

$\displaystyle\lim_{x\to a}f(x)=A$ と表す。また、

$x\to a$ のときに

$f(x)$ が極限を持つ(あるいは「

$f(x)$ が収束する」)とは、ある

$A\in\mathbb{R}$ が存在して、

$x\to a$ のときに

$f(x)$ が

$A$ に収束することをいう。

だった。
$a\in\bar{I}$ と距離が $\delta$ 未満であるような $x\in I$ に対して、 $f(x)$ と $A\in\mathbb{R}$ が十分近いときに $f$ は $A$ に収束する、ということだった。
この $A$ が $f(a)$ と一致しているときに「連続である」というわけなのである。

「あれ？なんかおかしいぞ？」と思うかもしれない。
「 $A$ って $f(a)$ のことじゃないの？」という疑問が湧くのではなかろうか。
実は違う。
例えばこんな例を考えてみる。

例4.
$u:\mathbb{R}\to\mathbb{R}$ が
$u(x)=\begin{cases} x+2&(x\in\mathbb{R}\setminus \{1\})\\ 1&(x=1) \end{cases}$
で定められていたとする。

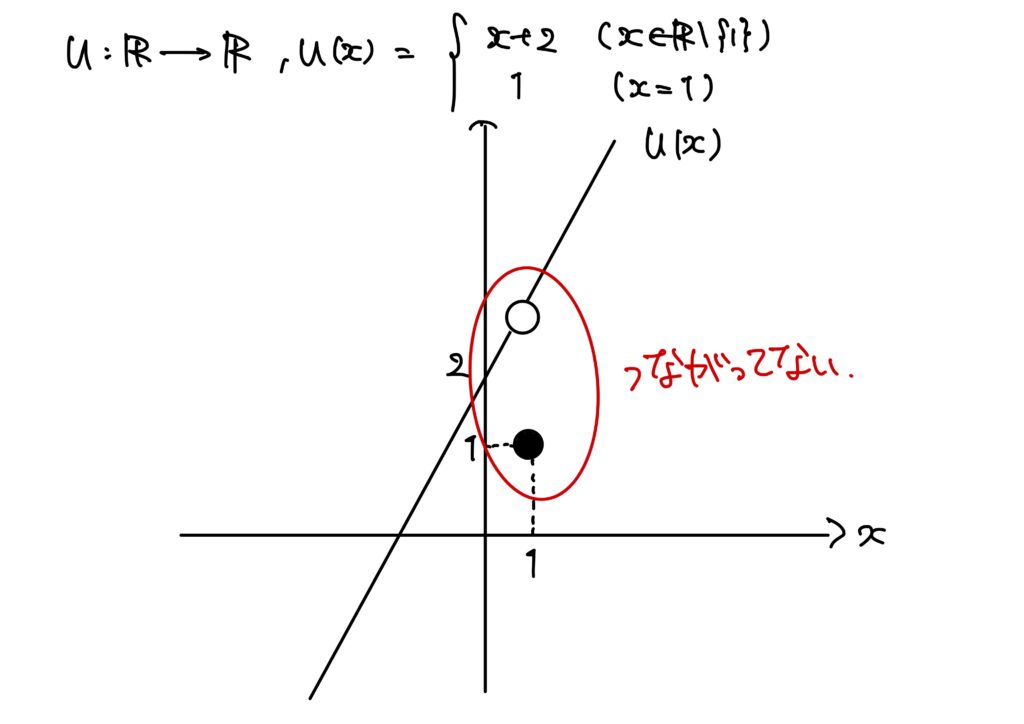
このとき、 $\displaystyle \lim_{x\to 1}u(x)=3$ である。
しかし、 $u(1)=1$ であるので、 $u(1)\neq3$ である。
すなわち、必ずしも $\displaystyle \lim_{x\to a}u(x)$ と $u(a)$ は一致しないのである。
ちなみに、この場合は $u$ は $x=1$ で連続でない(不連続であるともいう)。

結

今回は、関数の連続についてのイメージを説明した。

要は、

$f:I\to\mathbb{R}$ の点

$x\in I$ が

$x=a$ でつながっているときに、

$f$ は

$x=a$ で連続だ。

$a$ が

$I$ 内の任意の点であれば、

$f$ は

$I$ で連続だ。

ということである。

“つながっている”という言葉は極限を使って表現できる、というわけである。

次回は「関数の連続は数学的に何か。」を説明し、実際に関数が連続であることを証明してみる。

乞うご期待！質問、コメントなどお待ちしております！

この記事の内容をより詳しく知りたい方は以下のリンクの本を参照してください！
ちなみに「解析概論」は日本の歴史的名著らしいので、辞書的にもぜひ１冊持っておくと良いと思います！

コメントをする

Warning: Undefined variable $req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 32

Warning: Undefined variable $commenter in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Trying to access array offset on value of type null in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34

Warning: Undefined variable $aria_req in /home/nori9901/for-spring.com/public_html/wp-content/themes/cocoon-child-master/functions.php on line 34